光线追踪和纠缠光的产生——2021年亚洲物理奥林匹克竞赛理论第二题

房 颐 宋 峰

(1.南京师范大学附属中学 210003；2.南开大学物理科学学院 300071)

A.在各向同性电介质中的光传播

如果介质是各向同性的，我们有

其中，χ和ε＝ε0(1+χ)分别是介质的极化率和介电常量。对于各向同性介质中角频率为ω的光波，相位将沿→方向以速度(称为相速度)vp＝c/n传播，这里c是真空中的光速，n是介质的折射率。还可以使用射线来代表一束光波。光线的传播可以用电磁场能流的方向和速度vr来描述。

考虑均匀各向同性电介质中角频率为ω、波矢为的一个平面光波。

A.1 用ε和μ0来表示它的相速度vp。(0.4分)

A.2 对于该光波，电介质的折射率n是多少？(0.2分)

B.在单轴电介质中的光传播

现在，假设电介质是单轴的，即它沿介质中某个固定的特殊方向(称为光轴)是电各向异性的，我们现在将其称为z方向。在这种情况下，电位移和电场强度的关系为Dx＝εEx、Dy＝εEy和Dz＝ε＇Ez，其中x、y和z轴相互正交。因此，光波的相速度是各向异性的，还额外取决于→k和的方向。记，回答下列问题：B.1、B.2和B.3。

B.2 光波的偏振，即其电场的方向，可以垂直于xz平面(称为寻常光或o 光)或平行于xz平面(称为非寻常光或e 光)。对于在B.1 中找出的每个光波，将其偏振方向用单位矢量来表示，并判断它是寻常光还是非寻常光。再计算tanα，其中α是和之间的夹角(从到顺时针旋转时α为正)。(0.8分)

B.3 将B.1和B.2中的结果扩展到一般情况，→和z轴正方向之间的夹角仍然是θ，但→不在xz平面中。求出所有可能的折射率值和相应的偏振。(0.6分)

B.4 结合问题B.1-3，考虑一个光波，其→=k(sinθ，0，cosθ)。令→与射线的方向之间的夹角为αr(从到沿顺时针方向时αr为正)。求出tanαr、射线速度vr和的所有可能值。利用这些结果，用、和ne来表示射线折射率ns＝c/vr。(0.8分)

考虑光线通过各向同性介质(记为介质1)和各向异性介质(记为介质2)之间的界面，从A传播到B，如图1所示。该界面与yz平面重合，而入射平面为xz平面。令入射角为θ1。介质1的折射率为n，而介质2 在z2、y2、x2轴上的折射率分别为ne、no和no。这里y2轴与y轴重合。费马原理指出，光线从A到B的传播时间是最短的。对于偏振平行于xz平面并以角度θ1入射的光，由费马原理可得出以下方程式：

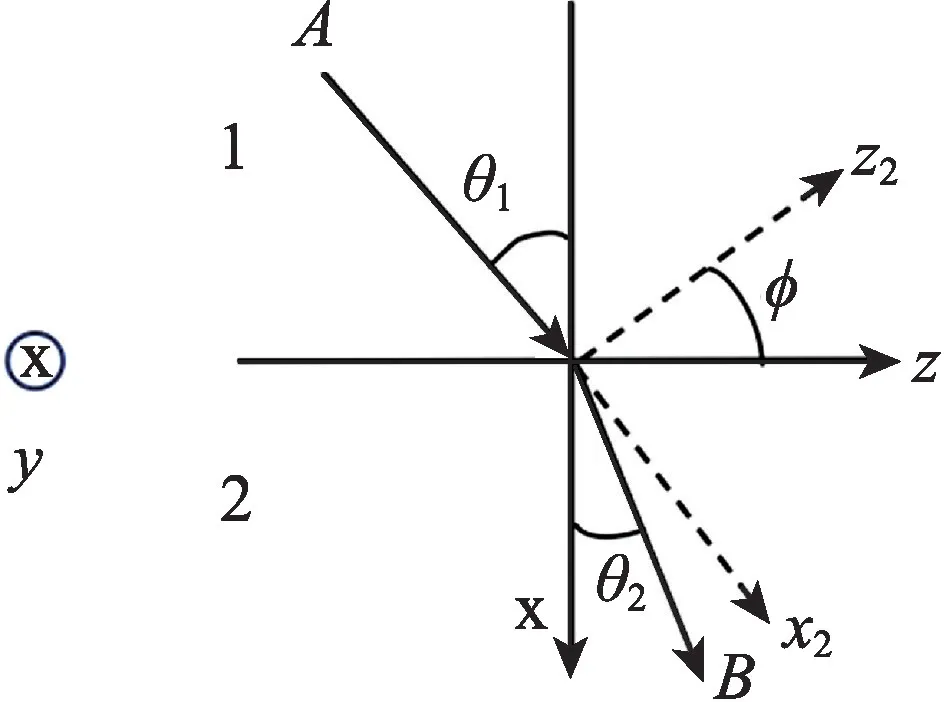
图1 光通过各向同性介质1和各向异性介质2之间的界面从A传播到B

C.光的纠缠

这里i、j、k可以是x、y、z三个分量中的任何一个，是代表介质的二阶非线性极化的常数。的存在意味着当光波通过非线性介质时，它可以分成两个光波。

C.1 找出这些角频率和波矢之间的所有可能关系(称为相位匹配条件)。将光视为由光子组成，这些条件对涉及的三个光子意味着什么样的守恒定律？对于角频率为ω，波矢为的光子被分成角频率为ω1和ω2，分别以波矢→和→传播的两个光子的情况，写出表示这些守恒律的方程。(0.8分)

C.2 考虑单轴介质中的光波。将寻常光线记为o，将非寻常光线记为e。有8种可能的光波分裂方式：o→o+o，o→e+o，o→o+e，o→e+e，e→o+o，e→e+o，e→o+e，e→e+e。假设折射率no和ne都是ω的递增函数。使用与问题C.1中相同的波矢符号，并考虑→→→ 共线的情况，请指出这8种分裂方式中哪些是不可能的。(0.8分)

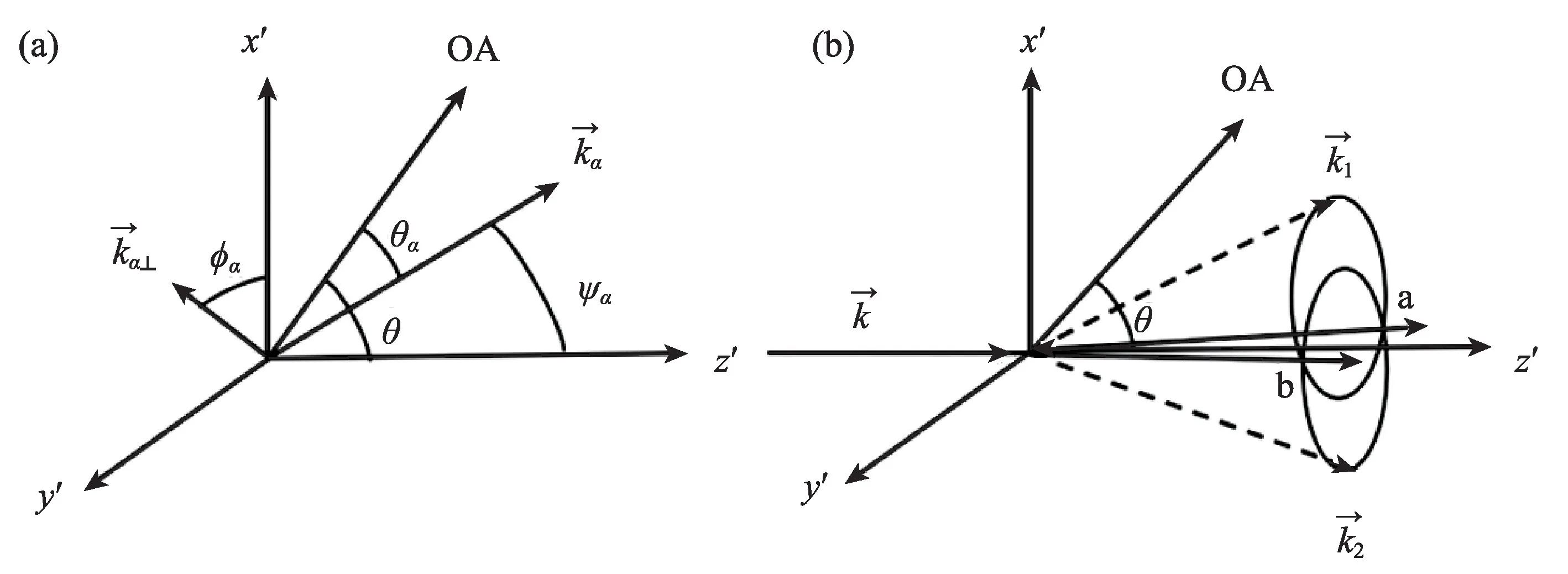
图2：(a)→矢量在x＇y＇z＇坐标系中具有角坐标(ψα，φα)，→是其在x＇y＇平面上的投影。注意到→与光轴OA的夹角为θα。(b)e光非共线分裂为e光+o光，从而形成两个圆锥。直线ab平行于y＇轴。

问题C.3 表明，一个光子可能会分裂为两个光子，当通过a 点和b 点时，它们的偏振方向互相垂直。这两个光子称为纠缠光子对，因为如果通过a的一个光子(称为a光子)的偏振沿＇方向，则通过b的另一个光子(称为b光子)的偏振将沿方向，并且如果a 光子偏振沿方向，则b 光子偏振将沿＇方向。纠缠光子对可以通过实验得到。它是以上两个备用状态的叠加，可以表示为。这 里表示a 光子的偏振沿'方向且b光子的偏振沿'，对于同理。系数可以看作是a 光子和b 光子的电场振幅(以合适的单位表示)的乘积。如图3 所示，两个线偏振片1和2的透射轴相对于'分别成α和β角度。我们可以使用它们对通过a和b的两个光子进行同时测量。将同时找到通过偏振片1和2的两个光子的概率记为P(α，β)。或者，P(α，β)也可视为与通过两个偏振器的光(在适当的叠加之后)的强度的乘积成正比。将α+π/2和β+π/2分别表示为α⊥和β⊥。

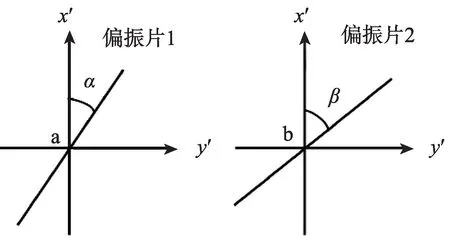
图3 两个线偏振片1和2，用于对通过a和b的光子进行符合测量

C.4 考虑透过线偏振片的总电场，求出概率P(α，β)、P(α，β⊥)、P(α⊥，β)和P(α⊥，β⊥)。(0.8分)

C.5 当偏振片1 以α角探测到一个a 光子时，令σa=1，当偏振片1 以α⊥角探测到一个a 光子时，令σa=-1。类似地，当偏振片2以β或β⊥角探测到一个b光子时，令σb=1或-1。若E(α，β)表示σaσb的平均值，物理量S=|E(α,β)-E(α,β＇)|+|E(α＇,β)+(α＇,β＇)|有重要的意义。在光的经典理论中，S≤2。这是Bell 不等式的变形(Clauser-Horne-Shimony-Holt不等式)。求出S的表达式，求出α=π/4、α＇=0、β=-π/8、β＇=π/8情形下的S值。指出S与经典理论是否一致。(0.5分)

背景知识介绍

1.晶体的各向异性：晶体与非晶体的重要区别是晶体在不同的空间方向上表现不同的物理特性，称为各向异性。构成晶体的分子或原子按一定方向排成周期性结构，整个晶体结构可看成是结点(原子或分子)沿空间不同方向按一定距离平移而成，因不同方向周期不同，所以晶体物理性质与方向有关，即晶体的介电常数以及折射率是与方向有关的。

图4

2.晶体双折射：当光入射到各向同性介质(如水、玻璃等)的分界面上时遵从折射定律，折射光只有一束，即只成一个像。当光入射到各向异性介质(如冰、方解石、石英等晶体)的分界面上时，一般会产生两束折射光，即可以观察到双像(如图)，其中一束光满足通常的折射定律，称为寻常光(o 光)，另一束光不满足折射定律，称为非寻常光(e光)。双折射是由晶体中各向异性的原子间结合力导致的，即在某些方向上原子之间存在较强的吸引力。

图5

3.光轴：在晶体中存在某个特殊方向，光在晶体中沿这个方向传播时不发生双折射，即o 光和e 光不分开，传播速度相等，该特殊方向称为晶体的光轴。常见的单轴晶体有天然方解石、石英、红宝石，以及人工拉制的ADP(磷酸二氢氨)、铌酸锂(LiNiO3)等；双轴晶体有云母(Mica)、蓝宝石(Sapphire)、黄玉(Topaz)等。

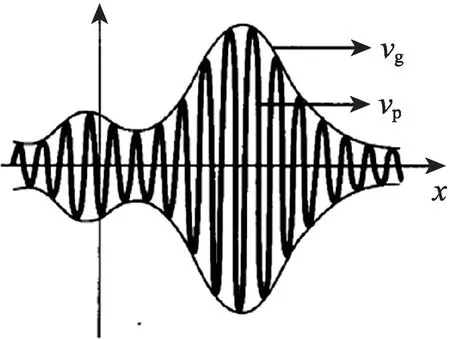
图6

5.纠缠态：量子力学允许两个或更多的粒子以共享状态存在，无论它们相距多远。当两个粒子处于纠缠的量子态时，测量其中一个粒子的属性，就可以立即确定对另一个粒子进行等效测量的结果，而无需检验。自量子力学理论提出以来，这一直是争论最多的内容之一。爱因斯坦称之为鬼魅般的超距作用，薛定谔则说它是量子力学最重要的特征。2022 年诺贝尔物理学奖授予阿兰·阿斯佩(Alain Aspect)、约翰·弗朗西斯·克劳泽(John Francis Clauser)、安东·塞林格(Anton Zeilinger)，以表彰他们通过光子纠缠实验，确定贝尔不等式在量子世界中不成立，并开创了量子信息这一学科。