基于 OAM 光束的球形颗粒的手性信号增强机理

孙阳　胡海峰

摘要：为了分析球形颗粒的手性信号增强机理，基于 T 矩阵法对手性球形颗粒的 Mie散射特性进行了研究，分析了基于入射光束轨道角动量（OAM）的调控和颗粒特性参数调控的手性信号增强机理。对紧聚焦线偏振光的波前进行调控，通过调控光束携带 OAM 的符号实现 OAM 二色性的测量，并研究 OAM 阶数与手性信号强度之间的关系。当光束携带 OAM 的阶数与小球的尺寸相匹配时得到较圆偏振光散射圆二色性信号22.8倍的提升。同时分析了小球特性参数（颗粒尺寸、手性参数）对 OAM二色性信号的影响。

关键词：轨道角动量；Mie 散射；T 矩阵；手性测量；光场调控

中图分类号： O 434.14 文献标志码： A

Enhancement mechanism of chiral signal from spheres based on OAM beams

SUN Yang，HU Haifeng

（School of Optical-Electrical and Computer Engineering， University of Shanghai forScience and Technology， Shanghai 200093， China）

Abstract： In order to analyze the mechanism of chiral signal enhancement of spherical particles， the Mie scattering characteristics of spherical particles are studied based on the T-matrix method， and the mechanism of chiral signal enhancement is analyzed based on the regulation of incident beam with orbital angular momentum （OAM） and particle s characteristic parameters. The wave front of tightly focused linearly polarized light is regulated， the dichroismofOAM is measured by regulating the sign of OAM carried by the beam， and the relationship between the order of OAM and the intensity of the chiral signal is studied. When the order of the OAM carried by the beam is matched with the size of the sphere， the scattering circular dichroism signal can be enhanced by 22.8 times compared to that of circularly polarized light. The influence of particle size and chiral parameters on OAM dichroism signal is also analyzed.

Keywords： orbital angular momentum； Mie scattering ； T matrix ； measurement of chirality；field manipulation

引言

手性是自然界的基本属性。如果一个物体与其本身的镜像不同，即其镜像不能与原始物体重合，该物体可以被称为手性物体[1-2]。许多生物分子是手性的，如氨基酸、脂肪。手性分子及其镜像分子被定义为对映体。由于对映体可能具有不同的毒性，所以如何区分对映体在制药工业中非常重要[3]。由于它们的特性在很多方面都相同，如组成元素种类、分子量、化学键等，因此手性异构体必须与另一手性物质发生作用时才能对其进行区分。圆偏振光由于携带自旋角动量从而具有手性[4-5]，电场矢量沿着传播方向顺时针旋转是左旋圆偏振光，逆时针旋转是右旋圆偏振光。由于手性异构体对左旋和右旋圆偏振光（CPL）的反应不同，因此人们可以利用手性效应来实现区分[6]。圆二色性（CD）就是这些效应的一个典型例子[7]。CD 信号可以表示为 g =2（A+? A?）/（A++ A?），其中 A+和 A?是分子对左旋、右旋圆偏振光的吸收效率[8]。由于分子尺寸通常远小于光学波长，这导致 CD 信号的强度（即 g 因子）很小，很难测量[1]。

目前，已经有很多研究者对如何提升手性信号开展了相关工作。这些研究表明，手性信号的强度不仅与分子的手性特征有关，还与入射光场的手性有关[2]。2018年，Yao 等[9]通过设计硅立方体结构，基于两个硅立方体间的狭缝能激发电场热点与磁场热点，可获得较圆偏振光15倍的光场手性信号提升。2019年， Hu 等[10]基于 Richards-Wolf 矢量衍射積分法，对携带轨道角动量（OAM）的径向偏振光经高数值孔径物镜聚焦后的焦场进行计算，结果显示在透镜焦点处可研究表明光场手性与手性信号强度成正比，所以提升光场手性能有效提升分子的手性信号[2]。但是通过提升光场手性信号去提升分子手性信号只适用于瑞利分子，即分子尺寸远小于波长的情况。对于尺寸接近波长甚至大于波长的结构，其手性信号不仅与光场特性有关，还与手性结构特性、大小等参数有关。上述通过提升光场手性的方法对于大尺寸的结构就不再适用。

手性信号的测量必须通过两束手性相反的光束分别激发手性结构，通过手性结构对两束具有相反手性光束响应的相对差别，实现手性信号的测量。除了使用左旋、右旋圆偏振光之外，也可以通过改变入射光的螺旋形等相位面的方向（即光子 OAM 量子数的符号）实现结构手性特征的测量，即 OAM 二色性测量[11-12]。在这项工作中，我们基于 T矩阵法对手性小球的 Mie散射特性进行研究，解释了基于入射光束 OAM 调控的手性信号增强机理。本文选用具有 OAM 的紧聚焦线偏振光作为入射光场，将手性小球放置于入射光场的焦点位置处，通过改变 OAM 的符号实现 OAM 二色性的测量，再通过调控 OAM 的阶数来提高 Mie散射球形颗粒的手性响应。最后讨论了颗粒本身特性参数与 OAM 二色性之间的关系。

1 紧聚焦光场计算

选取携带 OAM 沿 X 方向偏振的线偏振光束作为入射场[13]，在柱坐标系中，这个入射场可以表示为

式中： E0为振幅因子； l 为拓扑荷数。利用Rachards-Wolf 衍射积分公式计算出焦点处的获得较圆偏振光11.9倍的光场手性信号提升。场分布表达式为[14-16]

式中： A 是与焦距和波长相关的常数；k=2π/λ 是真空中的波数； ），n0 为空气折射率，NA 为聚焦透镜的数值孔径大小；P（θ）是透镜的切趾函数，可表示为

式中：β0=1 ； J1是一阶的第一类贝塞尔函数。

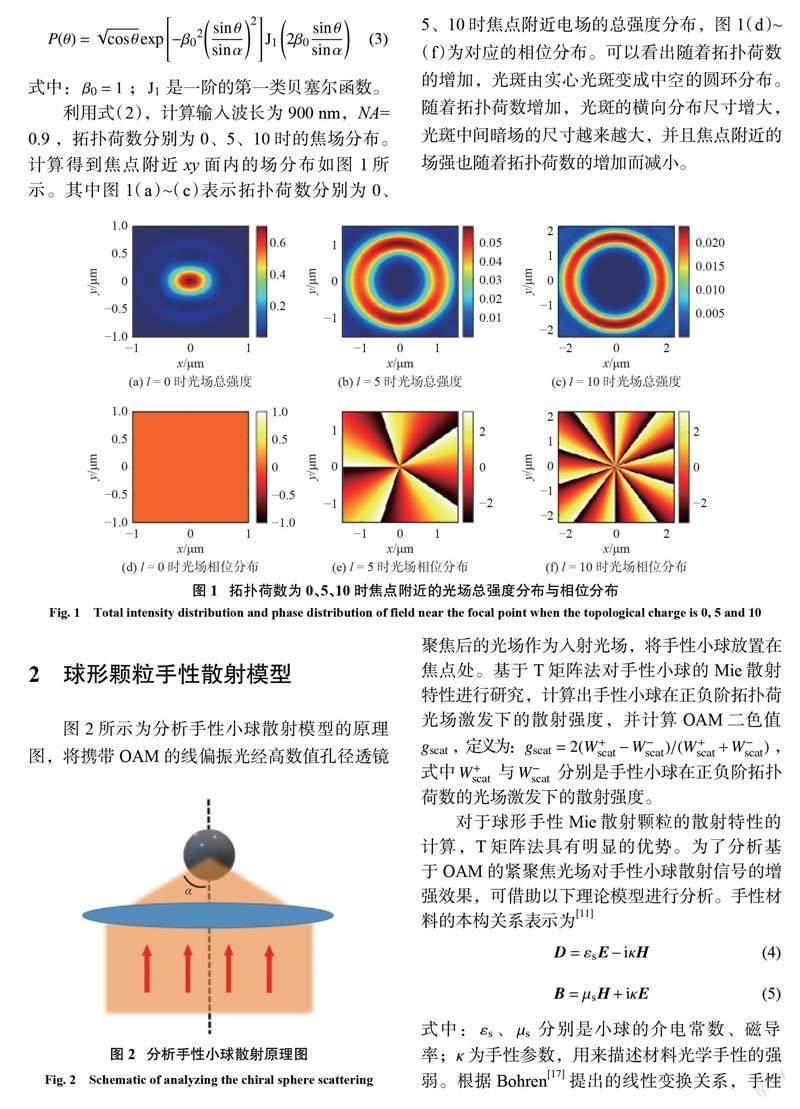
利用式（2），计算输入波长为900 nm，NA=0.9，拓扑荷数分别为0、5、10时的焦场分布。计算得到焦点附近xy面内的场分布如图1所示。其中图1（a）～（c）表示拓扑荷数分别为0、5、10时焦点附近电场的总强度分布，图1（d）～（f）为对应的相位分布。可以看出随着拓扑荷数的增加，光斑由实心光斑变成中空的圆环分布。随着拓扑荷数增加，光斑的横向分布尺寸增大，光斑中间暗场的尺寸越来越大，并且焦点附近的场强也随着拓扑荷数的增加而减小。

2 球形颗粒手性散射模型

图2所示为分析手性小球散射模型的原理图，将携带 OAM 的线偏振光经高数值孔径透镜聚焦后的光场作为入射光场，将手性小球放置在焦点处。基于 T 矩阵法对手性小球的 Mie散射特性进行研究，计算出手性小球在正负阶拓扑荷光场激发下的散射强度，并计算 OAM 二色值gscat，定义为：gscat =2（W at ? W at ）/（W at at ），荷数的光场激发下的散射强度。

对于球形手性 Mie散射颗粒的散射特性的计算， T 矩阵法具有明显的优势。为了分析基于 OAM 的紧聚焦光场对手性小球散射信号的增强效果，可借助以下理论模型进行分析。手性材料的本构关系表示为[11]

式中：εs 、?s 分别是小球的介电常数、磁导率；κ为手性参数，用来描述材料光学手性的强弱。根据Bohren[17]提出的线性变换关系，手性小球中的电磁场（E1 ， H1）可以表示为以下形式：

式中：kL/R =ω4εs?s士ωκ; m 与 n 是矢量球谐函数阶数。在本研究中，RgMmn与RgNmn用来表示无奇点的矢量球谐函数，Mmn与Nmn表示用于散射场展开的具有奇点的矢量球谐函数[18]。在手性球的外部，入射场（E inc ， Hinc）与散射场（Es， Hs ）可以表示为矢量球谐函数的组合：

在式（9）与式（10）中，展开系数umn与vmn由入射场决定。基于 T 矩阵法，可根据入射场的展开系数umn与vmn计算散射场的展开系数。根据手性球表面的边界条件（r = Rs ），手性球体的 T 矩阵可由下式得出：

其中矩阵 T（1）与 T（2）的各项元素由下式给出：

在式（14）～（21）中，第一类球贝塞尔函数定义为ψn（ρ）=ρjn（ρ），第三类球贝塞尔函数定义为ξn（ρ）=ρhn （1）（ρ）。Z0是真空中的阻抗， k0=ω/c 是真空中的波数。基于 Mie散射理论，散射强度可以根据散射系数由下式计算：

3讨论与分析

利用上述理论模型研究了散射强度与光束拓扑荷之间的关系并使用 MATLAB 软件完成仿真计算，仿真结果如图3所示。其中入射光波长为900 nm，手性小球的折射率为1.5，手性小球的半径为1.9?m，手性参数κ为±0.01，拓扑荷的变化范围是?20～20。图3（a）与图3（b）分别表示左手结构与右手结构时散射强度与光束拓扑荷之间的关系，图3（c）表示左手结构与右手结构时散射 CD 信号与光束拓扑荷之间的关系。可以看出不论是左手结构还是右手结构，散射强度随着拓扑荷数的增加而减小并逐渐趋近于0，这是因为拓扑荷数变大会导致焦点附近的场强越来越弱，且光斑中间暗场的尺寸越来越大，导致照射在手性小球上的光强越来越弱，散射强度也越来越弱。OAM 光束的手性信息包含在其螺旋形等相位面中，可通过调控光束 OAM 阶数来改变其螺旋形等相位面大小。对于尺寸固定的手性颗粒，当 OAM 光束螺旋形等相位面的大小与颗粒尺寸相当时，分子与光子 OAM 的手性相互作用最强烈。正如图3（c）所示，左手结构与右手结构的散射 CD 信号在拓扑荷为0～2与14～17范围内有显著提升，并且在拓扑荷数为1和17时有明显的峰值。当拓扑荷数为17的时候，散射CD 信号达到最大值。这是因为光束的拓扑荷数与手性颗粒的尺寸相匹配时，手性颗粒对光场的手性响应最强。

为了分析不同尺寸的手性小球 OAM 二色性与拓扑荷数之间的关系，分别计算了小球半径为1.4?m 、1.5?m 、1.6?m 、1.7?m 、1.8?m、1.9?m 时基于圆偏振光的散射 CD 信号以及紧聚焦线偏振光的 OAM 二色性，其中入射光波长为900 nm，小球折射率为1.5，手性参数κ为 0.01。同时計算得出入射光束具有不同拓扑荷时，基于紧聚焦光场测得的手性信号较圆偏振光入射条件下手性信号强度的增强因子，如图4所示。图4（a）表示随着小球的尺寸变大，紧聚焦线偏振光情况下的 OAM 二色性的峰值信号也向更大的拓扑荷数位置处移动，证明了手性信号与拓扑荷数的匹配机制。图4（b）为小球半径为1.4?m 、1.5?m 、1.6?m 、1.7?m 、1.8?m 、1.9?m 时在圆偏振光入射下的散射 CD 信号。从图4（c）可以发现，随着小球的尺寸变大，手性信号增强因子的峰值也向更大的拓扑荷数位置处移动，并且当小球的尺寸为1.7?m 时，在拓扑荷数为15时得到最大值22.8。此结果表明，为了获得更大的手性信号强度，入射光束的拓扑荷数要与球形颗粒的尺寸相匹配。

手性信号增强因子不仅与入射光场有关，还与球形颗粒本身的特性参数有关，因此进一步计算了不同手性参数值情况下的散射手性信号。计算了手性参数κ分别取0.01、0.02和0.03时的散射手性信号，其中入射光波长为900 nm，手性小球折射率为1.5，手性小球半径为1.9?m，结果如图5所示。可以看出当拓扑荷数为17时不同的手性参数κ对应的散射手性信号都达到最大值，并且随着手性参数κ的增大，不同手性参数κ对应的信号最大值也逐渐增强。

4 结论

本文基于 T 矩阵法对手性小球的 Mie散射特性进行了研究，与瑞利散射相比，Mie 散射能准确描述球状手性结构的散射特性。结果表明，为了实现手性信号的提升，需要使 OAM 阶数与小球尺寸相匹配。本文针对特定尺寸的球形颗粒，通过优化入射光束 OAM 阶数，理论上得到的手性信号强度比常规的圆偏振光场得到的散射 CD 信号提升了22.8倍。另外在手性小球尺寸与 OAM 阶数相匹配的情况下提升手性小球本身的手性参数，可以在不改变散射 CD 信号峰值位置的前提下，进一步提升手性信号强度。因此，为了增强手性信可以从远场和近场两方面入手，在远场对入射光场进行调控，在近场优化设计手性结构，并实现两者之间的匹配。本文中的理论模型将有助于手性信号增强机理的分析以及物质手性光学探测方法的研究。

参考文献：

[1] MUN J， KIM M， YANG Y， et al. Electromagnetic chirality： from  fundamentals  to  nontraditional chiroptical  phenomena[J].  Light：  Science  & Applications， 2020， 9：139.

[2] TANG Y Q， COHEN A E. Optical chirality and its interaction with matter[J]. Physical Review Letters， 2010， 104（16）：163901.

[3] ZHAO Y， ASKARPOUR A N， SUN L Y， et al. Chirality detection of enantiomers using twisted optical metamaterials[J]. Nature Communications， 2017， 8：14180.

[4] TANG Y Q， COHEN A E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light[J]. Science， 2011， 332（6027）：333–336.

[5] NI J C， LIU S L， WU D， et al. Gigantic vortical differential scattering as a monochromatic probe for multiscale chiral structures[J]. Proceedings of the National Academy of Sciences of the United States of America， 2021， 118（2）： e2020055118.

[6] KIM M， RHO J. Plasmonic-enhanced chirality examined by generalized wavenumber eigenvalue simulation[J]. Optics Express， 2018， 26（11）：14051–14057.

[7] ROSALES-GUZM?N C， VOLKE-SEPULVEDA K， TORRES J P. Light with enhanced optical chirality[J]. Optics Letters， 2012， 37（17）：3486–3488.

[8] HU H F， ZHAN Q W. Enhanced chiral Mie scattering by a dielectric sphere within a superchiral light field[J]. Physics， 2021， 3（3）：747–756.

[9] YAO K， LIU Y M. Enhancing circular dichroism by chiral hotspots  in silicon  nanocube dimers[J]. Nanoscale， 2018， 10（18）：8779–8786.

[10] HU H F， GAN Q Q， ZHAN Q W. Generation of a nondiffracting superchiral optical needle for circular dichroism imaging of sparse subdiffraction objects[J]. Physical Review Letters， 2019， 122（22）：223901.

[11] HU H F， ZHAN Q W. Chirality measurements using orbital angular momentum of light[J]. Chinese Journal of Quantum Electronics， 2022， 39（2）：272–285.

[12] HU H F， GAN QQ， ZHAN Q W. Achieving maximum scattering circular dichroism through the excitation ofanapole states within chiral Mie nanospheres[J]. Physical Review B， 2022， 105（24）：245412.

[13] GANIC D， GAN X S， GU M. Focusing of doughnut laser beams by a high numerical-aperture objective in free space[J]. Optics Express， 2003， 11（21）：2747 –2752.

[14] KIM J， WANG Y， ZHANG X. Calculation of vectorial diffraction in optical systems[J]. Journal of the Optical Society of America A， 2018， 35（4）：526–535.

[15] YOUNGWORTH K S， BROWN T G. Focusing of high numerical aperture cylindrical-vector beams[J]. Optics Express， 2000， 7（2）：77–87.

[16] ZHAN Q W. Cylindrical vector beams： from mathematical concepts to applications[J]. Advances in Optics and Photonics， 2009， 1（1）：1–57.

[17] BOHREN C F. Light scattering by an optically active sphere[J]. Chemical Physics Letters， 1974， 29（3）：458–462.

[18] MISHCHENKO M I， TRAVIS L D， LACIS A A. Scattering， absorption， and emission of light by small particles[M]. Cambridge： Cambridge University Press， 2002.

（編辑：张磊）