基于波像差理论的实数编码遗传算法优化XUV 光学系统

曾涛　吕丽军

摘要：由镜和光栅组成的 XUV 光学系统具有平面对称的性质，结合 Lu平面对称光栅系统的波像差理论和均方根像差评价函数得到用以优化 XUV 光学系统的多参量目标函数。为求解该多自变量且大取值区间的目标函数，提出了一种基于十进制的实数编码遗传算法，并将其用于两种 XUV 光学系统的优化求值。将求得的优化值用光学仿真软件 Shadow进行追迹，并和参考文献进行对比。结果显示本文优化后的光学系统在成像质量上有明显上升，表明波像差理论及本文的实数编码遗传算法可以有效地优化 XUV 光学系统，为此类系统的优化设计提供了新的思路。

关键词：波像差理论；实数编码；XUV 光学系统；点列图

中图分类号： TN 23；TH 744；O 435 文献标志码： A

Optimization of XUV optical system by real-coded genetic algorithm based on wave aberration theory

ZENG Tao，LYU Lijun

（Department of Precision Mechanical Engineering， Shanghai University， Shanghai 200072， China）

Abstract： The XUV optical system composed of mirrors and gratings has the property of plane- symmetry. Combining the wave aberration theory of the Lu plane symmetric grating system and the root mean aquare aberration evaluation function， the multi-parameter objective function for optimizing the XUV optical system is obtained. In order to solve the objective function with multiple independent variables and a large value interval， a real-coded genetic algorithm based on decimal is developed in this paper， and it is used for the optimization of two XUV optical systems. The optimized value obtained is traced with the optical simulation software Shadow， and compared with the reference. The results show that the optical system optimized in this paper has a significant improvement in imaging quality， indicating that the wave aberration theory and the real-codedgenetic algorithm in this paper are effective in optimizing the XUV optical system， which provides a new idea for the optimal design of such systems.

Keywords： wave aberration theory；real number coding；XUV optical system；spot diagram

引言

在同步輻射研究中，基于平面对称布置的 XUV 光学系统有着重要的应用[1]。不同的文献中对 XUV 的定义颇为不同，本文将 XUV 定义为从软 X 射线到极紫外波段的光源。超短脉冲的 XUV 光源具有高的空间分辨率和时间分辨率，有助于人们获得晶体、分子结构和电子轨道的结构信息和动力学信息，进而更好地认识物质世界[2]。在以往的 XUV 光学仪器设计中，人们倾向于选择在某个固定工作波长的条件下，分别使由光程函数得到的几个像差（目标函数）达到最小，或在一定波长范围内相互抵消[3-4]。这对于单个光学元件的优化设计来说是准确且有效的，但是当光学元件数量增多，且光学元件的子午焦点与弧矢焦点不重合时，光程函数发展而来的像差系数并不能准确描述 XUV光学系统最终的成像位置[5]。因而针对多元件光学系统成像的精确像差理论以及对成像质量进行分析评价的目标函数在 XUV 仪器设计中显得格外重要。

2008年，吕丽军教授在Chrisp的全息光栅波像差理论[6]的基础上发展了多个光学元件的平面对称光栅系统的波像差理论（Lu 波像差理论）[7]，这个理论对入射光源在光学元件表面的孔径光线采取了线性近似处理，采用多项式拟合得到了比光线追迹解析法更简洁的成像像差计算公式，非常适用于具有平面对称特性的 XUV 光学系统的成像。1994年，Koike 等[5]提出了对光栅系统成像点列图进行像质评估的均方根（rms）评价函数，它的定义为成像点在光谱色散方向（子午） rms 与垂直色散方向（弧矢）rms 的加权求和[5]。该评价函数纳入了所有可能的像差以及入瞳高度等因素，因而比以往的单个像差作为评价函数更具有优势。

在优化算法方面，过去的光学系统设计常采用阻尼最小二乘法，但该算法是一种局部优化算法，遇到极值容易过早收敛[8]。遗传算法因具有隐含并行性和全局搜索能力强等特点[9-10]，在当前的光学系统优化设计中得到了广泛应用。徐挺等[11-12]在优化极紫外光谱仪时采用了一种基于二进制编码的合作型协同进化遗传算法，提高了常规遗传算法的寻优能力，但当搜索空间较大时种群仍会过早收敛陷入局部极值。王泽民等[13]在优化超大视场光学系统时，在实数编码遗传算法的基础上混入了逃逸函数，改善了算法的鲁棒性。方翔等[14]在优化鱼眼镜头时将自适应变异概率加入实数编码算法中，并将参数进行归一化处理，从而大大提高了算法脱离局部极值的能力。本文采用实数编码遗传算法，并结合逃逸函数以及自适应变异概率来提高全局寻优能力。

本文拟对一个单元件的全息球面光栅单色仪和一个具有前置超环面聚焦镜的超环面全息光栅光谱仪进行优化设计：将平面对称光学系统的波像差理论和 rms 评价函数结合得到本设计的非线性多元目标函数，在波像差理论的基础上发展伴有逃逸函数的自适应归一化实数编码遗传算法，并用其对目标函数进行优化求值。第1节主要介绍 Lu 波像差理论以及其在像质评价函数中的应用，第2节阐述本文运用的实数编码遗传算法，第3节分析待优化的两套光学系统的相关设计参数并对其进行优化，运用光学仿真软件 Shadow 对本文优化结果和参考文献[15]的结果进行对比验证分析。结果表明本文建立的针对 XUV 光学系统进行优化的算法求取的结果对提高系统的成像质量有明显的效果。

1 Lu 波像差理論与 rms 像差评价函数

1.1 多光学元件系统的 Lu 波像差理论

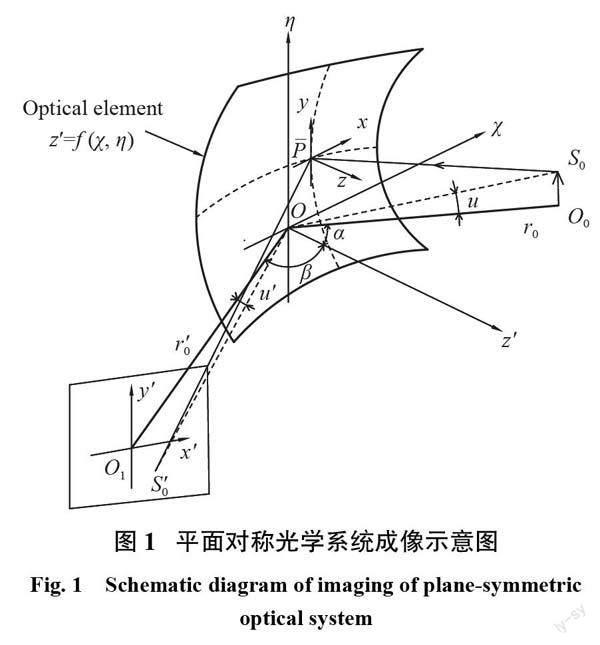
Lu 波像差理论是在单个元件被主光线斜入射的基础上得到各像差系数。此处说明各物理参量的意义。图1为其平面对称元件的光学成像示意图。其中，超环面光学元件（镜或光栅）的顶点位于点，是用于描述该元件表面形状的坐标系，原点位于，且是系统的对称平面。是一个平面外的光源，发出的主光线与光学元件表面交于点，反射后成像于点。在点建立的坐标系称为孔径（aperture stop）坐标系，用以描述入射光线在光学元件表面的位置，其 z 轴沿着点处的法线方向。光源在对称平面的投影为，对称平面内的称为基光线。垂直于的像平面为，为像平面上的像点，场角（field angle）和分别表示和的夹角、和的夹角，为入射角和反射角，为物距和像距。

当存在多个光学元件时，图 2 为连续相邻的光学元件在弧矢平面中的光路示意图。一般的光学元件面的形状可由如下四阶方程[7] 表达，为面形系数：

u 和 γ 一般都非常小，且通常用 γ 表示物方视场角，表示物方弧矢焦距，表示物方子午焦距。为了表征在 η 轴的方向与点 O 的距离，引入一个非物理参量：

由图 2 中的几何关系容易导出如下关系式：

式中：；。本文中参数带有一撇（'）则表示的是像方参数，。以上参数将用于波像差系数中。文献 [7] 给出系统的总波像差 W 为

式中：wijk是波像差系数，由物方波像差系数Mijk（α; rm ; rs; l）和像方波像差系数Mijk（β; rm（′）; rs（′）; l′）组成；Mijk由文献[7]的式（78）～（93）给出；ΛNijk项考虑了光栅刻槽的影响，对于镜元件该项的值为0，Λ=（）Γ ， m 是光栅级次，λ是工作波长，系数Nijk和光栅刻槽密度分布系数nij相关，文献[7]的表1给出了Nijk的表达式，Γ和nij由文献[16]的式（20）～（22）给出。

由文献[7]的下述像差公式可以得到图1像平面 x′ O1y′上任一已知入射光线的像点位置：

式中：dijk和hijk叫作横向像差系数，由文献[7]的式（94）～（113）给出； x和 y 是入射光线在光学元件表面的照射点在孔径坐标系xyz中的坐标； u为物方场角。当系统中存在多个光学元件时，成像公式（8）中各参数都应替换成被入射光线照射的最后一个光学元件的物理参数。如何从一个元件的位置参数计算得到最后一个元件的相应参数，需要用到相关的转化系数。对于有 n 个光学元件的系统，第 h（h =1，2，··· ， n-1）个元件与第 n 个元件由文献[7，17-18]给出了如下转换关系式

式中： x（h）、y（h）、 u（h）为光线在第 h 个光学元件上的投影点坐标和场角； A（h）、 B（h）是第 h 个元件与最后一个元件间的转换系数。由上述公式，系统总波像差 W[式（9）]的计算可以转化为最后一个元件的波像差计算：

式中： Wijk是总波像差系数；wijk（h）是第 h 个光学元件的波像差系数。现在，对于多元件光学系统的成像计算来说，式（8）也同样适用，只需要在求dijk、hijk时，用式（14）的Wijk替换wijk，其他物理参数用最后一个光学元件的参数。至此已完成平面对称的多元件光学系统任意一条入射光线的成像数值计算。

1.2 rms 像差评价函数

当光学系统最终成像的像面坐标可以由式（8）确定后，我们就可以对成像点进行像质分析。对于某一工作波长λt 下物距为 r0的物点光源，可以追迹有限数量的点。参考文献[5]定义的 rms 像质评价函数为

式中：！是衡量像点的 x′对 y′相对重要性的权重因子（！<1）。X、Y 是第一个光学元件表面被入射光照射的区域在孔径坐标系xyz中的xOy面上投影的宽度和高度。在 XUV 光学仪器中，入射光的主光线一般会经过光学元件的中心 O，即图1中点 P（?）和点 O 会重合，故 x 和 y 的积分域是对称的（（? ;）、（? ;））。 x′用于衡量像点在 x′方向上的平均分散程度，由于此类光学系统是水平对称的，所以 y′方向平均分散程度 y ′积分计算后为0。U 是考虑入瞳高度时物点光源对光学元件的场角。将式（8）和式（17）代入式（16）和式（18）就得到本文的优化目标函数 Q（λt ）的关键两项Qx′（λt ）、Qy′（λt ）的表达通式：

目标函数 Q（λt ）有一个很重要的特点：完全由系统中各光学元件的物理参数决定。这给我们后续优化光学元件的结构参数指明了方向。为了使仪器光谱分辨率更高，成像应该越小越好，即选择最佳的光学元件结构参数使目标函数 Q（λt ）达到最小。在优化 XUV 光学仪器时，通常在工作波长范围内选择 n 个波长同时进行优化，最终的像质评价函数 Q 为

式中ε（λt ）是各波长λt 对应的像质权重因子。

2 混入逃逸函数的自适应归一化实数编码遗传算法

本文像质评价的非线性目标函数公式（21）中，在设计之初先确定常量 X、Y、U，那么变量就完全由各像差系数dijk、hijk组成，而这些像差系数又是只和光学系统中各个镜或光栅的物理参数相关，如何选择各物理参数使得像质评价函数最小的问题实际上是多元函数求最小极值的问题。光学设计领域中常用的牛顿迭代法和阻尼最小二乘法在求极值时很容易陷入局部极值的尴尬，在近年来的文献调研中，遗传算法（GA）被广泛用于多参量的光学系统的设计中，其寻优能力较以往的方法有很大改善。

传统的二进制编码（编码符号集为{0，1}）的 GA 在优化多维高精度连续函数时存在如下缺点：1）表示同一变量域时，二进制代码串比十进制代码串长很多，同时还要频繁地编码和解码，极大地增加了计算量和内存，导致算法运算效率低[19]；2）当变量域较大时，若采用较短的二进制编码长度则会人为地将连续变量空间离散化（比如相邻的两个编码串对应的变量差值可能相差好几个整数量）[14]，该类编码串大概率会遗漏最优解，若采用长的编码串虽然可以提高精度，但却导致 GA 的运算量急速增大，寻优能力下降；3）实数域下相邻的整数变量对应的二进制编码可能有很大的海明距离，但欧氏距离很小，也就是海明悬崖问题[20]，这会影响交叉和变异操作，从而降低遗传算子的搜索效率[13]。

为克服上述二进制编码存在的缺点，本文引入实数编码的遗传算法（ RCGA）来求解目标函数的极值。实数编码（编码符号集为{0，1，2，···，9}）采用解空间的形式进行编码，以变量的取值数来确定编码长度，与同精度的二进制编码串相比短很多，能对整个寻优空间进行搜索，且保持足够的精度。将每个变量均编码到[0， 1）内的實数范围，相当于一个归一化的过程，取各小数位作基因。以自变量取值[0， 600]为例，可取编码位数为4，编码归一化为0.0000～0.9999，对应的编码则是0000～9999，相邻的两个编码对应的变量差值约为0.06，则能达到0.1的精度，编码位数为其他值时亦可同理计算。

本文的适应度函数采用式（21）的倒数，采用轮盘赌选择算子，交叉算子采用均匀交叉和多点交叉并行的方式，变异算子采用基因变异。 RCGA 的交叉、变异算子没有二进制编码灵活，摆脱局部极值的能力较弱，因此考虑改善不同适应度个体的变异能力、提高算法搜索能力，在基因变异阶段，引入文献[21]中的自适应公式来动态调整种群中各个体的变异概率：

式中：Pm 是个体的变异概率； f 是个体的适应度；favg是种群的平均适应度； Pm_ max 和Pm_min是预设的最大与最小变异概率，这里分别为0.1和0.025。 fmax 一favg是用来衡量算法的收敛程度的尺度，当算法收敛到局部最优， fmax 一favg值减小，Pm 会增大，从而使算法尽快脱离局部最优。 fmax 一f 是衡量个体优良程度的尺度，当个体的适应度 f 低于种群的平均适应度favg时，说明个体性能不好，此时取最大的变异概率；而性能好的个体的适应度高于favg， fmax 一f 也较小，取较小的变异概率来保证优良个体不因变异而被破坏[21]。

为了进一步增强算法跳出局部极值的能力，本文引入逃逸函数，其思想是当算法搜寻到一个已知的局部极小值时，在逃逸函数的影响下，此时“局部地形”发生改变，从而跳出极小值[13]。逃逸函数表达式如下：

式中： xi是第i个优化参量；xiL是用不带逃逸函数的 RCGA 得到的第i个优化参量的极小值。H 和 W 的值通过 k、次试验计算得到，初值 H0=0.8 ， W0=0.1。图3是本文的算法流程图。

3 XUV 光学系统优化实例

3.1 球面全息光栅单色仪的优化

当超环面光栅或者变线距光栅被用于 XUV 光学系统设计时，光学元件的数量可以减少，而单个光学元件的单色仪一般可以通过采用球形或者超环面光栅来实现[4]。文献[15]给出了图4所示的固定偏转角的 XUV 单色仪装置，其主要的光学工作元件是一块变线距球面全息光栅，工作点光源 A 以及全息刻录相干点光源 C、D 均位于对称平面内，此时孔径坐标系xyz与全局坐标系χηz、重合，场角 u 为0，且参量 l =一l、=0。全息记录的角度参数δ、γ和记录波长λ0要满足关系式

由于该单色仪装置的光学元件面形为半径已知的球形，并且放置参数（α、β、r0、r0（、））也预先固定，那么待优化的参数只剩下光栅的全息记录参数（δ、γ、rc、rd），这几项与式（7）相关。由式（25）可以得到δ和γ的关系，则待求参数变为（δ、rc、rd）。

系统的总体参数见表1，固定偏转角 K =α一β=69.733O ，某一工作波长为λ的光源入射角α和衍射角β要满足如下光栅方程（衍射级次m =一1）：

该单色仪工作光源的波长为200…600nm ，可以选择优化波长λ1=200 nm ，λ2=250 nm ，λ3=400 nm ，λ4=600 nm 代入目标评价函数[式（21）]，ε（λt ）均取1，ω取0.8。最终的目标函数可以抽象为 Q = Q（λ1）+ Q（λ2）+ Q（λ3）+ Q（λ4）= f（rc ; rd ;δ），在 MATLAB 中利用本文第2节所阐述的算法（RCGA）进行求解，计算20次的结果如图5所示。

取上述结果中的最小 Q 值对应的各个变量，则本文的优化结果如表2所示。

通过式（26）和式（27）可以求得不同波长光源的入射角和衍射角，利用几何关系可以求得在仿真软件中设置的光源发散角，如表3所示。在 MATLAB 中，将我们的优化结果代入基于波像差理论[式（8）]编写的点列图成像程序（追迹大约2500条光线），并在光学仿真软件 Shadow 中光线追迹模拟实际的成像结果，两者结果对比如图6所示。

3.2 前置超环面聚焦镜的超环面全息光栅光谱仪的优化

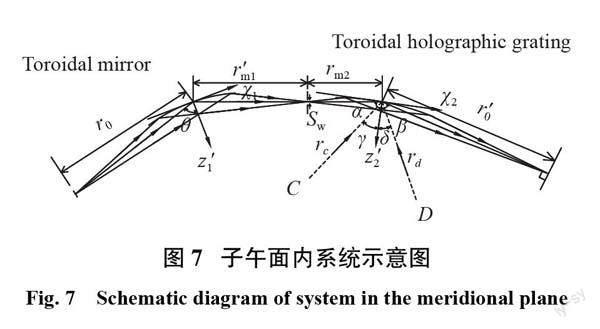
采取与3.1节相同的优化策略，对文献[15]给出的 XUV 光谱仪进行优化并和原文比较。该光谱仪具有平直的光谱聚焦面，适合用光电探测仪器测量空间分辨或时间分辨光谱[22]，故也称为平场光栅光谱仪。图7为该 XUV 平场光谱仪的系统示意图。光谱仪工作波段为3～6 nm，该波段的光源在光学元件表面的反射率极低，通常采用掠入射的方式提高反射率。其前置超环面聚焦镜可以有效地聚焦弧矢方向的能量，从而减小像散[23]；采用后置的选取了适当参数的全息光栅可以有效校正成像面子午方向的离焦。主光线通过第一个光学元件的中心，第一块元件对应的非物理参量 l1=?l1（′）=0，利用式（4）计算得到第二块光学元件对应的非物理参量 l2=?l2（′）= e ，其中 e 是两个光学元件间的间隔。

此系统由两个光学元件组成，所以要先利用式（14）计算系统的总波像差系数Wijk。其中光学元件间的转换系数 A 、B 计算公式为

然后利用式（8）计算系统最终的成像像差，在代入计算时，用总波像差系数Wijk代替dijk、hijk中的wijk ，其他参数使用最后一个光学元件的参数。

该系统的可优化参数为：前置聚焦镜的弧矢半径（ρ1），超环面全息光栅的子午方向与弧矢方向的曲率半径（R2、ρ2），全息光栅的记录参数（δ、γ、rc、rd）。根据式（25）可知，只需要求取6个参数（ρ1、R2、ρ2、δ、rc、rd）即可。其他的系统参数与参考文献相同，如表4所示。

取优化波长λ1=3 nm ，λ2=4：4 nm ，λ3=6 nm ，ε（λt ）依次取1、2、1，！取1，同时代入式（21）得到目标优化函数：

利用第2節所述算法对上式进行优化求解，结果如表5所示。利用 Shadow对本文的优化结果和文献[15]结果分别进行光线仿真追迹，如图8所示。

本文与参考文献的光线追迹点列图在水平方向、垂直方向的半峰全宽（FWHM）值（ F_X 、 F_Y ）对比如表6所示。

4 优化结果分析

球面全息光栅单色仪优化结果分析。对比图6的（A1、A2、A3、A4）与（B1、B2、B3、B4）点列图，可以看到由本文程序得到的点列图很好地描述了系统成像的位置，这也表明 Lu 波像差理论在预测系统成像像差上的准确性。对比图6的（B1、B2、B3、B4）和（ C1、C2、C3、 C4）点列图，在波长较短时，基于本文算法优化得到的系统参量能与参考文献达到近乎一致的成像品质，在工作波长较长时成像更为清晰。表2中可以看到本文优化得到的 Q 值比参考文献的数据得到的 Q 值略小。这说明本文采用的像质评价函数以及优化算法对于优化 XUV 光学系统的参量是有效的。

前置超环面聚焦镜的超环面全息光栅光谱仪优化结果分析。对比图8的（A1、A2、A3）和（B1、B2、B3）点列图，基于直观结果分析，本文优化值得到的像点在横向和纵向的像差均比参考文献值更小。一般以 FWHM 值作为成像分辨率的评价指标。基于表6进行定量分析，工作波长在3 nm 和6 nm 时，本文优化后得到的系统分辨率只在水平方向较优，而在中心工作波长4.4 nm 处，水平方向和垂直方向结果均优于参考文献的系统分辨率。利用式（30）计算可得本文优化后Qmine =1：6736，参考文献Qref =1：9105，再次验证了较小的目标函数值对于系统成像质量的提升是有效的。

5 结论

XUV 光学系统通常具有多个参量，且参量取值跨度大，将本文基于波像差理论的实数编码遗传算法应用于 XUV 光学系统的优化，可以得到各变量取值的较优组合，较以往的方法更易实现全局寻优。通过光线追迹验证了用本文方法优化得到的两种光学系统在成像质量上有一定程度的提升。当光学元件的数量增多时，依然可以结合 Lu波像差理论和 rms 像质评价函数得到目标函数，再用本文方法进行优化求解。综上，本文的研究具有延伸意义。

参考文献：

[1] ROSSBACH J， SCHNEIDER J R， WURTH W. 10 years of pioneering X-ray science at the free-electron laser FLASH at DESY[J]. Physics Reports， 2019， 808：1–74.

[2]牛永.基于高次谐波产生的极紫外光源及其辐射特性研究[D].长春：吉林大学， 2017.

[3] FABRIS N， MIOTTI P， FRASSETTO F， et al. A high resolution XUV grating monochromator for the spectral selection of ultrashort harmonic pulses[J]. Applied Sciences， 2019， 9（12）：2502.

[4] MIOTTI P， FABRIS N， FRASSETTO F， et al. Design and realization of a XUV plane-grating monochromator at variable included angle[J]. AIP Conference Proceedings， 2019， 2054（1）：060023.

[5] KOIKE M， NAMIOKA T. Merit function for the design of grating instruments[J]. Applied Optics， 1994， 33（10）：2048–2056.

[6] CHRISP M P. Aberrations of holographic toroidal grating systems[J]. Applied Optics， 1983， 22（10）：1508–1518.

[7] LU L J. Aberration theory of plane-symmetric grating systems[J]. Journal of Synchrotron Radiation， 2008， 15：339–410.

[8]杨勋， 石建川.光学系统阻尼最小二乘法及 RND 函数法自动优化程序[J].光电工程 ， 1992， 19（1）：21–26.

[9] ZHOU X P， HUANG X C， ZHAO X F. Optimization of the critical slip surface of three-dimensional slope by using an improved genetic algorithm[J]. International Journal of Geomechanics， 2020， 20（8）：04020120.

[10] WANG Y， WANG M， LI J， et al. Comparison ofgenetic algorithm and dynamic programming solving knapsack problem[C]//Proceeding of 2020 3rd International Conference on Algorithms， Computing and Artificial Intelligence （ACAI 2020）. Sanya： ACM， 2020：10.

[11]徐挺， 吕丽军.极紫外光谱仪光学系统的优化设计[J].光学学报， 2010， 30（9）：2646–2651.

[12]徐挺 ， 朱国强.基于波像差理论的光学系统评价函数[J].光学仪器， 2010， 32（3）：55–59.

[13]王泽民， 吕丽军.混入逃逸函数的实数编码遗传算法优化光学系统[J].光子学报， 2014， 43（6）：0622001.

[14]方翔， 吕丽军， 牛智全.采用自适应归一化实数编码遗传算法优化鱼眼镜头系统[J].光电子·激光， 2015， 26（4）：655–661.

[15] CHRISP M P. X-ray spectrograph design[J]. Applied Optics， 1983， 22（10）：1519–1529.

[16] NAMIOKA T， KOIKE M， CONTENT D. Geometric theory of the ellipsoidal grating[J]. Applied Optics， 1994， 33（31）：7261–7274.

[17] LU L J， LIN D L. Aberrations of plane-symmetric multi-element optical systems[J]. Optik， 2010， 121（13）：1198–1218.

[18] LU L J， DENG Z Y. Geometric characteristics of aberrations of plane-symmetric optical systems[J]. Applied Optics， 2009， 48（36）：6946–6960.

[19]张超群， 郑建国， 钱洁.遗传算法编码方案比较[J].计算机应用研究， 2011， 28（3）：819–822.

[20]巩固， 郝国生， 王文虎.基于海明距离改进的自适应遗传算法[J].江苏师范大学学报（自然科学版）， 2014， 32（4）：51–54.

[21]王银年.遗传算法的研究与应用：基于3PM 交叉算子的退火遗传算法及应用研究[D].无锡：江南大学， 2009.

[22] CHAMPEY P R， WINEBARGER A R， KOBAYASHI K， et al. The Marshall grazing incidence X-ray spectrometer （MaGIXS）[J]. Journal of Astronomical Instrumentation， 2022， 11（2）：2250010.

[23] KANG Y F， WANG C. Combined focusing and flat- field spectrometer system for extreme ultraviolet pulse[C]//Proceedings of the 10th  International Symposium on Photonics and Optoelectronics （SOPO 2017）. Guilin： Scientific Research Publishing， 2017：15?20.

（编辑：张磊）