“以阀代井”水电站水轮机控制策略改进研究

王 奎，余 波，欧 前，任海波，王罗斌

（西华大学，流体及动力机械教育部重点实验室，四川 成都 610039）

0 引 言

对于具有长有压引水管道的水电站来说，通常其水流惯性时间常数较大，很容易出现水轮机调节系统的大波动水力过渡过程不满足调节保证要求，小波动过渡过程的动态特性较差的问题。为了改善大、小波动过渡过程，工程上常采用的措施一般有设置调压井或安装调压阀以代替调压井［1，2］。采用设置调压井的措施，可以明显地减小水电站有压引水系统的水流惯性时间常数，这对改善水轮机调节系统的大、小波动过渡过程具有明显的效果。但是设置调压井的投资大，建设周期长，甚至会对环境造成一定的破坏［3，4］。对于安装调压阀这一措施，其在水电站出现大波动过渡过程时开启，可以有效地改善大波动水力过渡过程，且安装调压阀的成本低，建设周期短，维护方便。但是，由于其不能减小水流惯性时间常数，对水轮机调节系统的小波动过渡过程没有改善效果，造成水轮机调节系统动态特性较差并危及到机组和电网的安全稳定运行。因此早期的水电站对采用“以阀代井”这一措施持十分谨慎的态度［5］。

随着电网规模的不断扩大和众多大型水电站的投运，电网的稳定性得到显著的改善，“以阀代井”的措施在中小型水电站中再次受到关注。一些学者对 “以阀代井”水电站的小波动过渡过程进行了仿真分析［6-9］，并对采用的常规水轮机调速器控制参数进行了一定的寻优。结果表明，通过扩大调速器参数整定范围可使机组小波动过渡过程符合基本的安全要求，但是机组转速和水头波动仍然较为剧烈，即其动态特性仍旧不够理想。

门闯社等人［10］研究发现，孤网下的常规水电机组随负载扰动幅值增加系统稳定性下降的主要原因是PID 调速器的速度饱和，接力器动作速度受限制跟不上调节器的动作从而产生行程差。他们提出一种对调节器输出进行限幅的方法来改进水轮机的控制策略，使调速器与接力器减小行程差，提高系统的稳定性。此改进的控制策略可在一定范围内提高水电站小波动过渡过程的动态特性，但在针对大水流惯性时间常数的电站时，这种直接对调节器输出幅值进行限制的改进方式会影响机组动态响应的快速性。

故对于具有长有压引水管道的“以阀代井”水电站，可以寻找一种新的改进方法改进其水轮机控制策略，以改善其小波动过渡过程的动态特性。

1 常规水轮机控制策略小波动过渡过程动态响应分析

孤网运行的“以阀代井”水电站，在小波动扰动时，电站调节系统的动态特性会更差［11］。其系统常具有负载扰动幅值大、负载扰动频繁、稳定性差等特点［12］。分析孤网运行水电站小波动过渡过程的动态响应，可以更为明显的发现水电站小波动过渡过程动态特性较差的原因。

对水电站进行小波动扰动实验具有一定的危险性，且影响水电站的生产。通过构建水轮发电机组的数学模型［13-15］，采用数值模拟的方式可以更为简单的寻找到改善方法。

1.1 数学模型

对于孤网运行的“以阀代井”水电站小波动过渡过程而言，由于减压阀在小波动过渡过程不动作，其响应过程与一般常规水轮机的小波动过渡过程一致，故只需采用常规水轮机调节系统的数学模型即可。

常规水轮机调节系统的构建参考文献［1］，由有压引水道，水轮发电机组以及水轮机调速器等部分共同组成，其数学模型为：

其结构如图1所示。

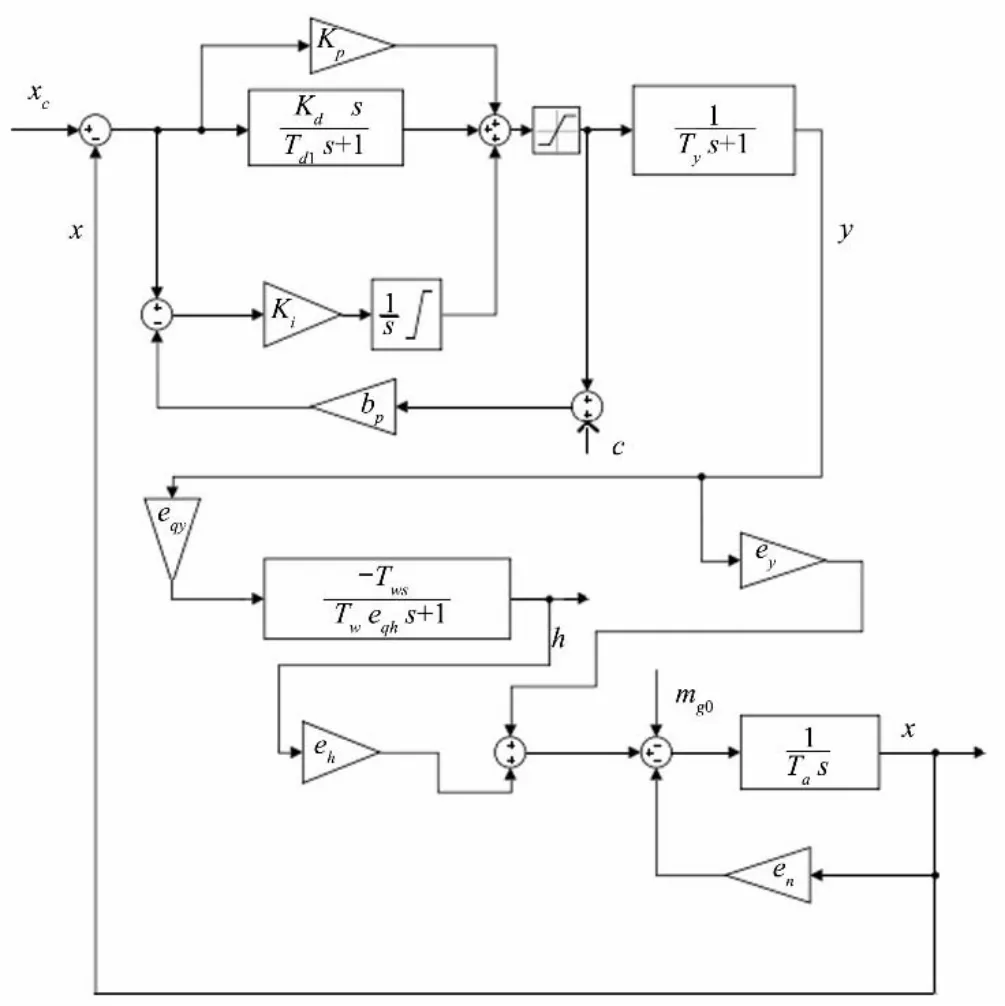
图1 常规水轮机调节系统结构Fig.1 Structure of conventional hydraulic turbine governing system

1.2 仿真计算

使用某小型电站的运行数据作为基本参数进行水轮机调节系统小波动过渡过程仿真计算。该电站的基本参数为：额定水头158.5 m，额定转速333.3 r∕min，额定流量31.75 m3∕s，水轮机额定出力45 MW，机组惯性时间常数为7.44 s，接力器时间常数0.2 s，水流惯性时间常数14.536 s。

针对负载工况，其水轮机6 个传递系数见表1。其调速器的PID参数设置见表2。基于图1和电站基本参数，采用Matlab∕Simulink 可构建该电站常规水轮机调节系统数字仿真模型［16，17］。以+10%的负载扰动信号为输入，设定水轮发电机组综合自调节系数为en=1.251，设定永态转差系数bp=0，进行数字仿真，其动态响应结果如图2、图3和图4所示。

表1 水轮机6个传递系数Tab.1 Six transfer coefficients of hydraulic turbine

表2 调速器PID参数Tab.2 PID parameters of governor

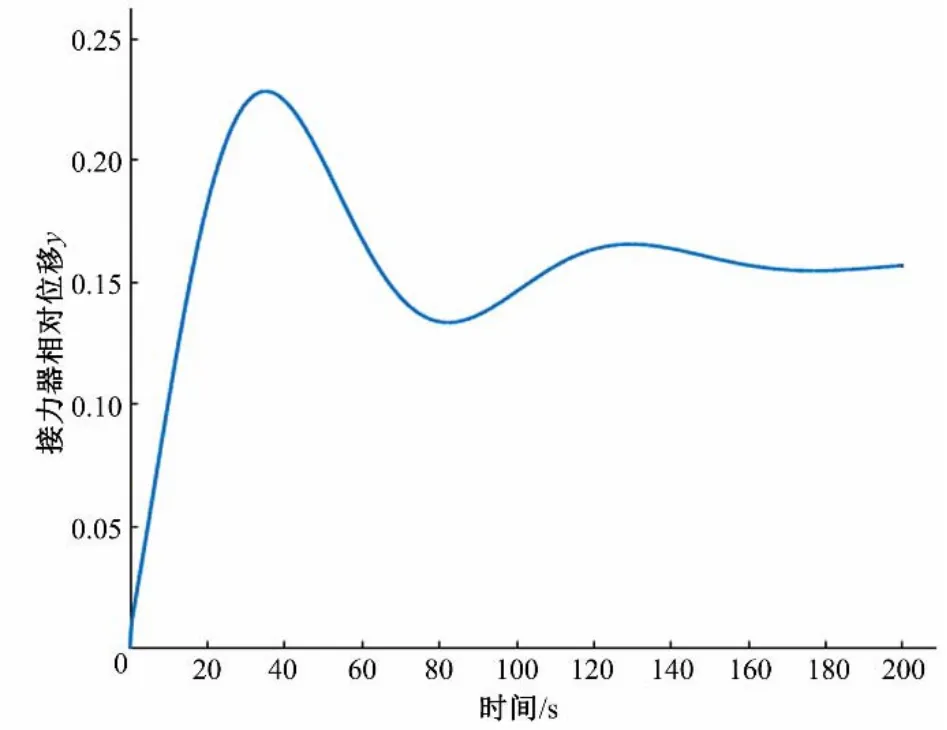
图2 常规调节系统小波动扰动接力器的动作响应Fig.2 Action response of small fluctuation disturbance relay in conventional regulation system

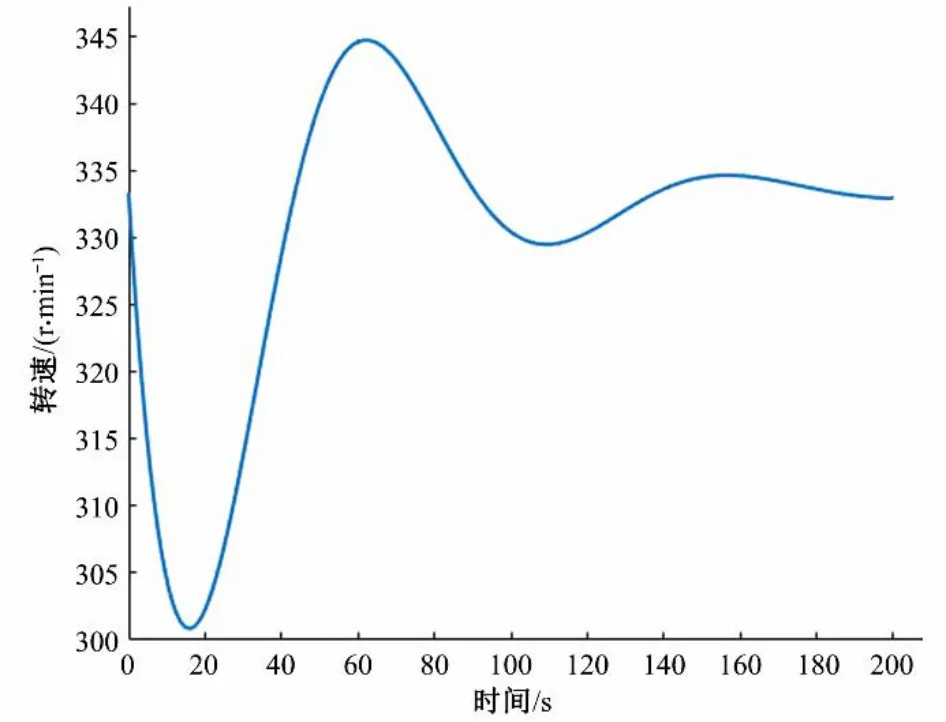
图3 常规调节系统小波动扰动机组的转速响应Fig.3 Speed response of small fluctuation disturbance unit in conventional regulation system

图4 常规调节系统小波动扰动水击压力的波动Fig.4 Fluctuation of water hammer pressure disturbed by small fluctuation of conventional regulating system

1.3 仿真结果分析

通过图2、图3 和图4，可以明显看到，常规的水轮机调节系统在小波动过渡过程扰动时，接力器前期的动作很频繁，动作幅度大。转速响应的超调量以及调节过程中的水压冲击也很大，且总体的调节时间过长，调节过程的动态性能不太理想。仿真结果表明，接力器的动作过快以及动作幅度过大，极有可能是造成水轮机调节系统在小波动过渡过程动态特性差的重要原因。这与门闯社等人得出的调速器速度过快的结论相符，故而需要考虑对调速器的速度进行限制。

1.4 仿真结果验证

将仿真使用的基本参数代入式（1），可得常规的水轮机调节系统的传递函数，根据此传递函数可绘制出常规的水轮机调节系统的开环对数频率曲线如图5所示。

图5 无反馈时的水轮机调节系统伯德图Fig.5 Bode diagram of hydraulic turbine governing system without feedback

由伯德图可见，增益交界频率为0.044 7 rad∕s，相位裕量为17.5°，而幅值裕量仅为2.2 dB，对比水轮机调节系统相位裕量和幅值裕量的推荐值可知，该系统的幅值裕量与相位裕量均较小，因此预示水轮机调节系统动态特性较差，与仿真结果一致。表明仿真结果具有一定的可靠性。

2 水轮机控制策略改进

2.1 改进方法分析

按照仿真结果分析，推测小波动过渡过程中产生冲击的重要原因是接力器的动作过于频繁、动作幅度过大致使导叶动作太剧烈。因此，可以考虑通过使导叶的动作过程更加平滑来改善其动态特性。通过对调速器进行改进，将接力器的位移信号作为一个反馈信号，在接力器动作过快时由调速器对其动作进行抑制，可以减小接力器的动作频率和幅度，从而使导叶的动作过程更加平滑，减小调节系统动作过程产生的冲击，进而改善小波动过渡过程的动态特性。

2.2 改进后系统的数学模型

由于信号的采集部位和反馈部位均只在调速器系统内，反馈信号引入前后只有调速器的数学模型发生变化，故以下仅讨论调速器数学模型的变化。对于常用的PID 型调速器，其控制环节包括比例环节（Kp）、积分环节（Ki）和微分环节（Kd），则信号引入方式有7 种组合。将反馈信号引入积分环节，相当于是增大了永态转差系数，不满足实际控制要求。故将接力器的行程信号按比例大小为Ky的负反馈方式引入调速器的比例和微分环节，产生一种新的水轮机控制策略，引入方式如图6所示。

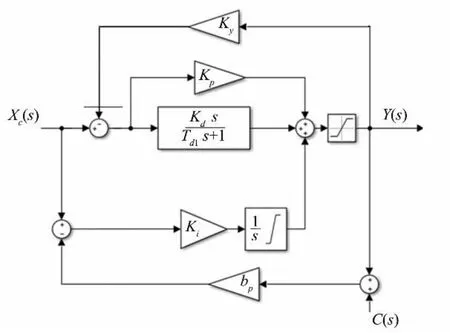
图6 引入反馈信号的调速器结构图Fig.6 Governor structure diagram with feedback signa

根据文献［1］可知，常规PID型调速器的数学传递函数为：

在bp=0时，常规PID型调速器的近似传递函数为：

如图6，对比例和微分环节引入反馈后，调速器的数学传递函数为：

在bp=0时，其调速器的近似传递函数为：

对比式（3）与式（5）可知，引入反馈信号的实质是调整了Kp以及Td1的取值，由于反馈的信号是随时变化的，所以Kp和Td1也在随时变化。故引入反馈信号相当于是对调速器参数进行实时寻优并实时修正。

对式（4）的分母进行处理后可得式（6）：

通过对比式（1）与式（6）分母二次项的系数，发现引入反馈信号后会导致时间常数增加，这会使调速器的动作速度变缓，从而使接力器的动作受到抑制，进一步表明引入接力器位移反馈改善水电站小波动过渡过程的理论是可行的。同时，时间常数增加表明系统的快速性会有一定的影响。

结合式（1）可得改进后的水轮机调节系统开环传递函数式（7）：

3 改进控制策略后水电站的小波动扰动仿真

3.1 数字仿真

对改进后的调节系统进行小波动扰动仿真，暂取反馈比例Ky=1，即以单位负反馈的方式引入反馈信号。

使用同样的基本参数对优化后的水轮机调节系统进行负载扰动为10%的小波动扰动仿真，其仿真结果及与常规型水轮机调节系统的响应对比如图7、图8和图9所示。

图7 引入反馈前后调节系统小波动扰动接力器的动作响应对比Fig.7 Comparison of action response of small fluctuation disturbance servomotor of regulation system before and after introducing feedback

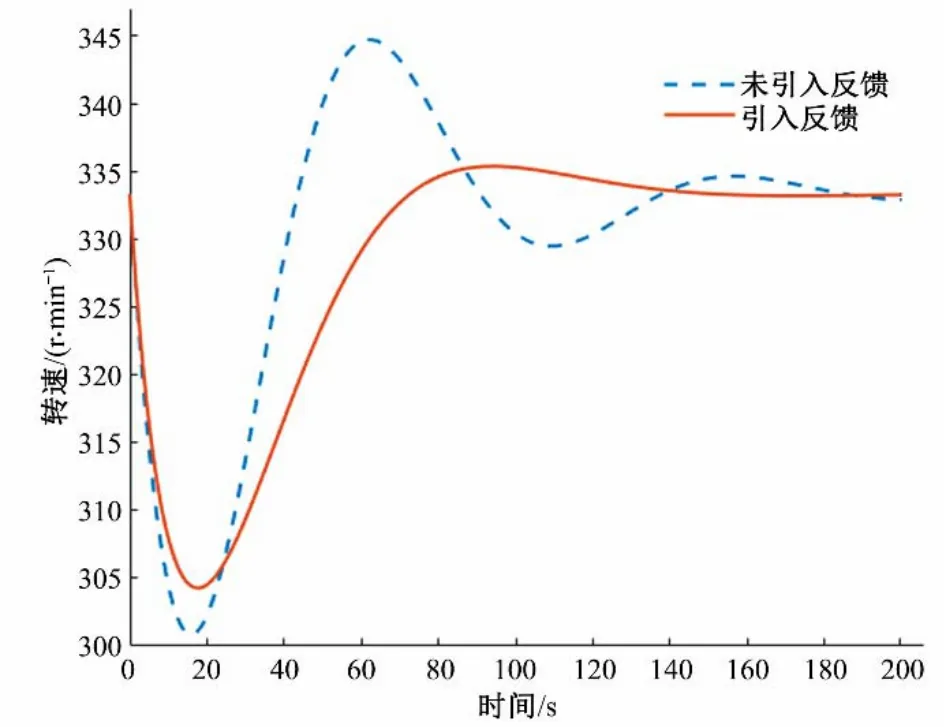
图8 引入反馈前后调节系统小波动扰动机组的转速响应对比Fig.8 Comparison of speed response of small fluctuation disturbance units of regulation system before and after introducing feedback

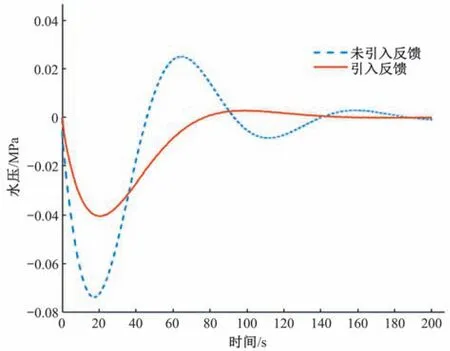
图9 引入反馈前后调节系统小波动扰动水压波动对比Fig.9 Comparison of small fluctuation disturbance water pressure fluctuation of regulating system before and after introducing feedback

3.2 仿真结果分析

通过仿真对比可得，在引入反馈信号之后，接力器的动作变得更为平缓，不再像之前那样反复动作多次才达到调节目的，机组的转速的超调量大幅度下降，水压的波动也大大减小，在降低调节过程中产生的冲击的同时，还缩短了调节时间，前后结果对比表明调节系统在小波动过渡过程的动态调节性能得到明显提升。证明该新型水轮机控制策略可有效改善具有长有压引水管道的“以阀代井”水电站调节系统在小波动过渡过程的动态调节性能。

3.3 仿真结果验证

通过基本参数绘制改进后的水轮机调节系统开环对数频率特性曲线验证仿真结果，将仿真使用的水电站基本参数代入式（7），可得改进后的水轮机调节系统传递函数，通过此传递函数可绘制改进后的水轮机调节系统开环对数频率特性曲线如图10所示。

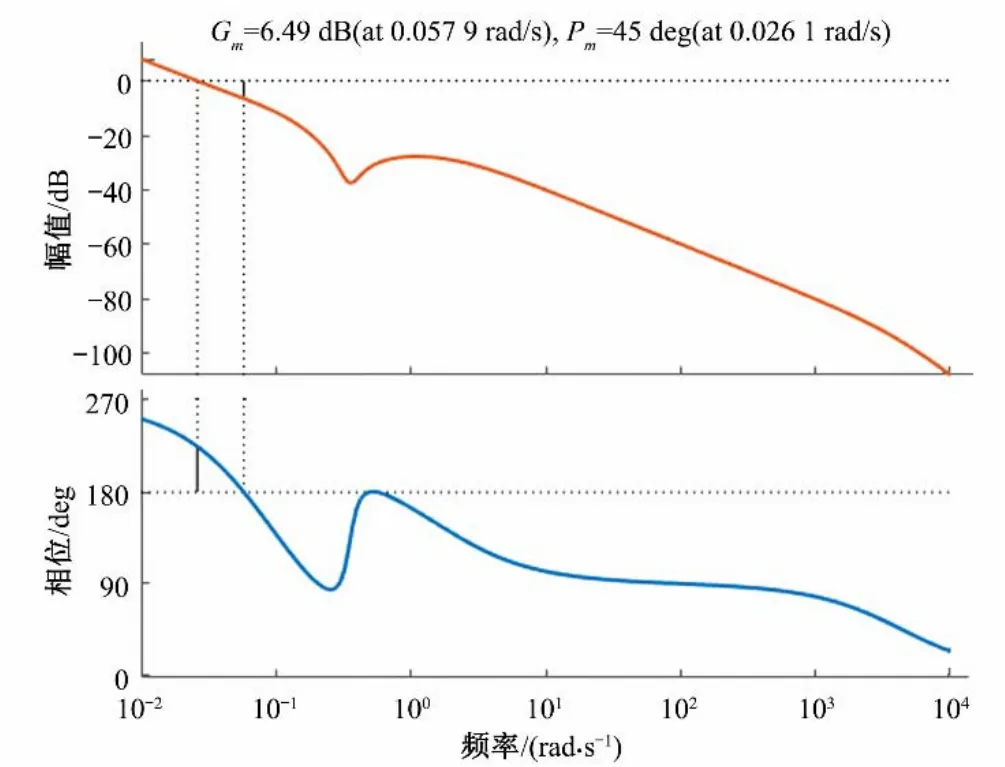
图10 引入反馈时的水轮机调节系统伯德图Fig.10 Byrd diagram of hydraulic turbine governing system with feedback

由图10 可知，增益交界频率为0.026 1 rad∕s，相位裕量为45°，幅值裕量为6.49 dB，对比水轮机调节系统相位裕量和幅值裕量的推荐值可知，该系统的幅值裕量与相位裕量均合适，因此预示水轮机调节系统动态特性较好，与仿真结果一致，表明仿真结果具有一定的可信度。

对比图10 与图4 可得，改进后的水轮机调节系统其相位裕量和幅值裕量增加明显，系统的动态性能得到了提升，但增益交界频率有所减小，其快速性略微有所下降，符合预期分析结果。

在调整Ky值的时候，发现以单位负反馈的方式引入反馈信号时，对系统调节性能的综合改善最大。

4 结 论

（1）传统水轮机调节系统在小波动过渡过程动态特性差的一个重要原因是在调节前期接力器的动作过快；

（2）将接力器的位移信号以单位负反馈的方式反馈到调速器的比例和微分环节，可以抑制接力器的动作，能有效减小调节过程中转速的超调量和水压的波动，对具有长有压引水管道的“以阀代井”型水电站小波动过渡过程的调节性能具有极大的改善；

（3）通过改进水轮机的控制策略与调压阀搭配的方式，可以改善调压阀的使用缺点，极大节省水电开发的投入；

（4）通过数字仿真验证了引入接力器位移信号反馈到调速器对小波动过渡过程的改善作用，后续可以设计实验加以验证。