不同坡度三种渠道下巴歇尔槽泥沙试验研究及数值模拟

曾钰峰，何新林，李小龙，杨 广，乔长录，金 瑾

（石河子大学水利建筑工程学院，新疆 石河子 832000）

0 引 言

巴歇尔量水槽作为灌区使用最广泛的量水槽，具有水头损失小，上游雍水程度低等优点。但其在淹没出流，横向沉降，纵向沉降［1］等条件下具有较大测流误差。灌区常见的3种渠道分别为梯形渠道、矩形渠道、U 形渠道［2，3］。同时新疆河流含沙量较大，灌区输水存在淤积情况［4］。所以探究巴歇尔量水槽在来沙下的适宜渠道及坡度，有利于提高实践中的量水精度，促进农业水价改革。

国内外学者对巴歇尔槽也做过一系列研究。KHOSRONEJAD 等［5］通过数值模拟和现场试验研究，量化了两个现场尺度巴歇尔量水槽的误差范围和水面波动。HEINER 等［6］通过试验发现在巴歇尔量水槽2∕3A 处进行水头测量时，误差可高达60%，同时，安装不正确及缺少翼壁设计会形成驻波，这也会影响流量测量的准确性。KIM 等［7］研究发现巴歇尔量水槽在估算枯水期的流量时比水位测量站的状态流量额定曲线方程更为精确。SAVAGE 等［8］通过物理实验和Flow-3D 模拟研究发现，当在巴歇尔量水槽规定以外的位置进行水位测量时，可能会出现高达60%的流量误差。同时，不同的入口翼墙配置也影响了巴歇尔槽的测流精度。许虎等［9］对不同进口连接段形式的巴歇尔槽进行了数值模拟，结果表明直面过渡段的巴歇尔槽测流精度较高。黄智刚等［10］通过对抛物线形量水槽和巴歇尔槽的水头损失对比分析，认为巴歇尔槽在U 形渠道上会产生较大的水头损失。THORNTON 等［11］将巴歇尔量水槽原始的测流方程进行了修改，开发了独特的方程用于测量超临界和亚临界流态的流量。前人对巴歇尔量水槽的自身几何结构和进口连接段的研究进行的较多，而缺少对巴歇尔槽适用性的研究。所以探究巴歇尔量水槽的适宜渠道及坡度对实践具有重要意义。同时分析巴歇尔槽在各工况下的过沙能力及测流精度，有利于指导新疆的灌溉输水及农业水价改革。

1 试验方案

1.1 试验布置

试验在石河子大学水利大厅进行，试验布置如图1所示，试验系统包括：泵房、电磁流量计、调节阀门、稳水池、闸门、U 形渠、矩形渠、梯形渠、巴歇尔槽、回水池、变坡控制系统等。水泵流量调节范围为0～0.1 m3∕s，根据明渠堰槽流量计计量检定规程JJG（水利）004-2015［12］及设计流量，选用喉道宽为0.152 m 的巴歇尔槽进行试验。其测流范围为0.001 5～0.1 m3∕s，符合设计要求。

图1 试验布置图（单位：m）Fig.1 Test layout

1.2 试验设计

查阅规范，0.152 m 喉道宽的巴歇尔槽临界淹没度为0.6。为保证试验为自由出流，先在未安装巴歇尔槽的渠道上进行水位～流量关系测定，试验最大流量为80 L∕s，梯形渠道、U 形渠道、矩形渠道0.1%坡度时的上游水深h上分别为：23.18，23.50，20.58 cm。即巴歇尔槽底槛最低高度P为［13］：

式中：P为底槛高度，cm；h上为未安装巴歇尔槽时的渠道正常水深；ha为巴歇尔槽上游测点处水深。

所以为保证3种渠道均为自由出流，设置底槛高度为5 cm。L1=4P，L5=6P，渠道的具体设计尺寸及巴歇尔槽尺寸见表1及图2～图4。

表1 巴歇尔槽结构尺寸图mTab.1 Structural dimension drawing of Parshall flume

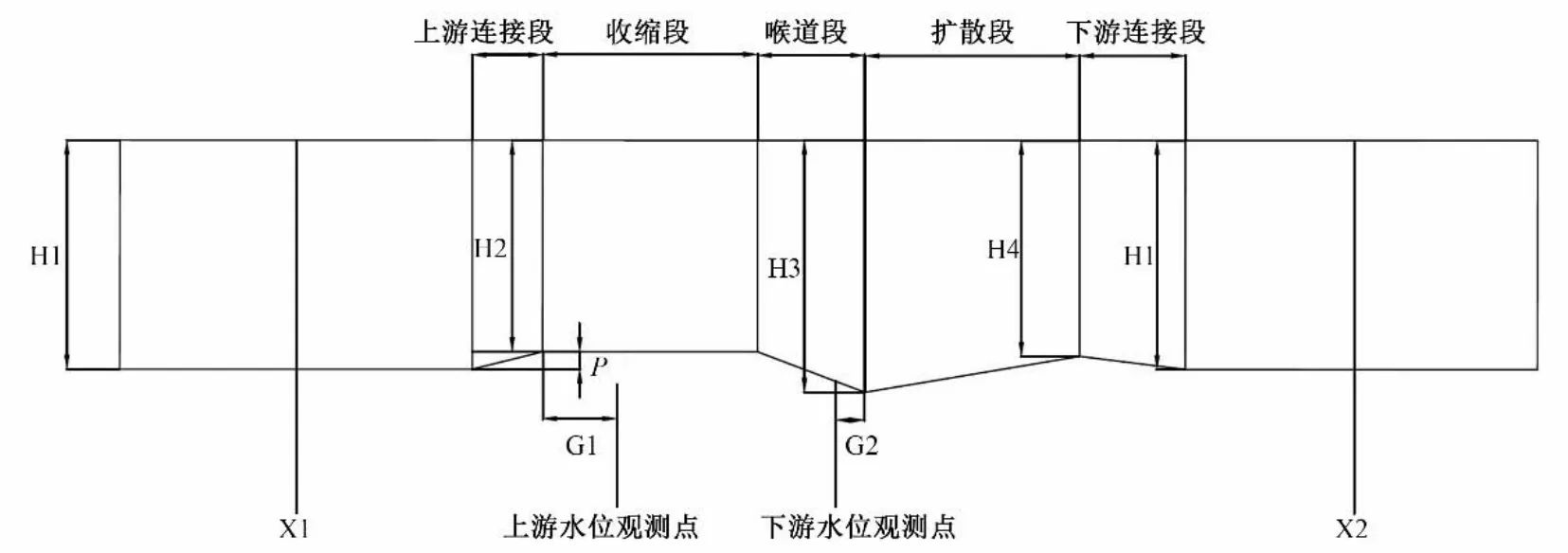
图2 渠道及巴歇尔槽纵剖面图Fig.2 Longitudinal section of channel and Parshall flume

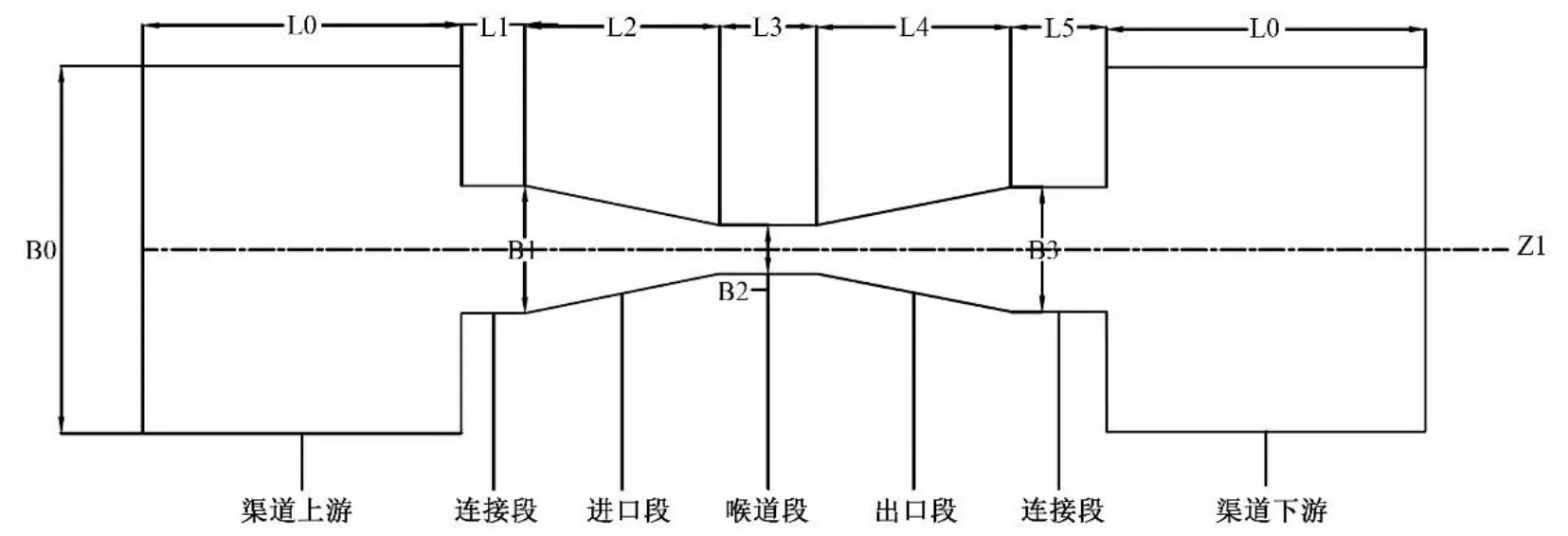
图3 渠道及巴歇尔槽俯视图Fig.3 Top view of channel and Parshall flume

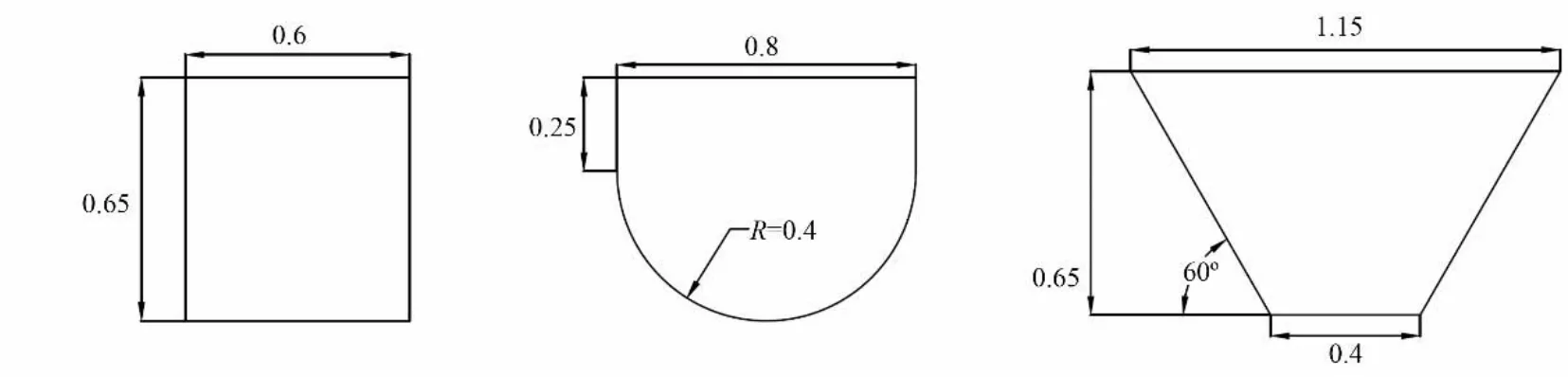
图4 3种渠道横截面图（单位：m）Fig.4 Cross section of three channels

渠道为钢结构，糙率为0.012。流量控制采用流量控制系统（DCMS），如图5所示。水位检测采用超声波探头及雷达水位计，如图6、图7 所示。流速测量采用多普勒流速仪，如图8 所示，变坡控制系统如图9所示。

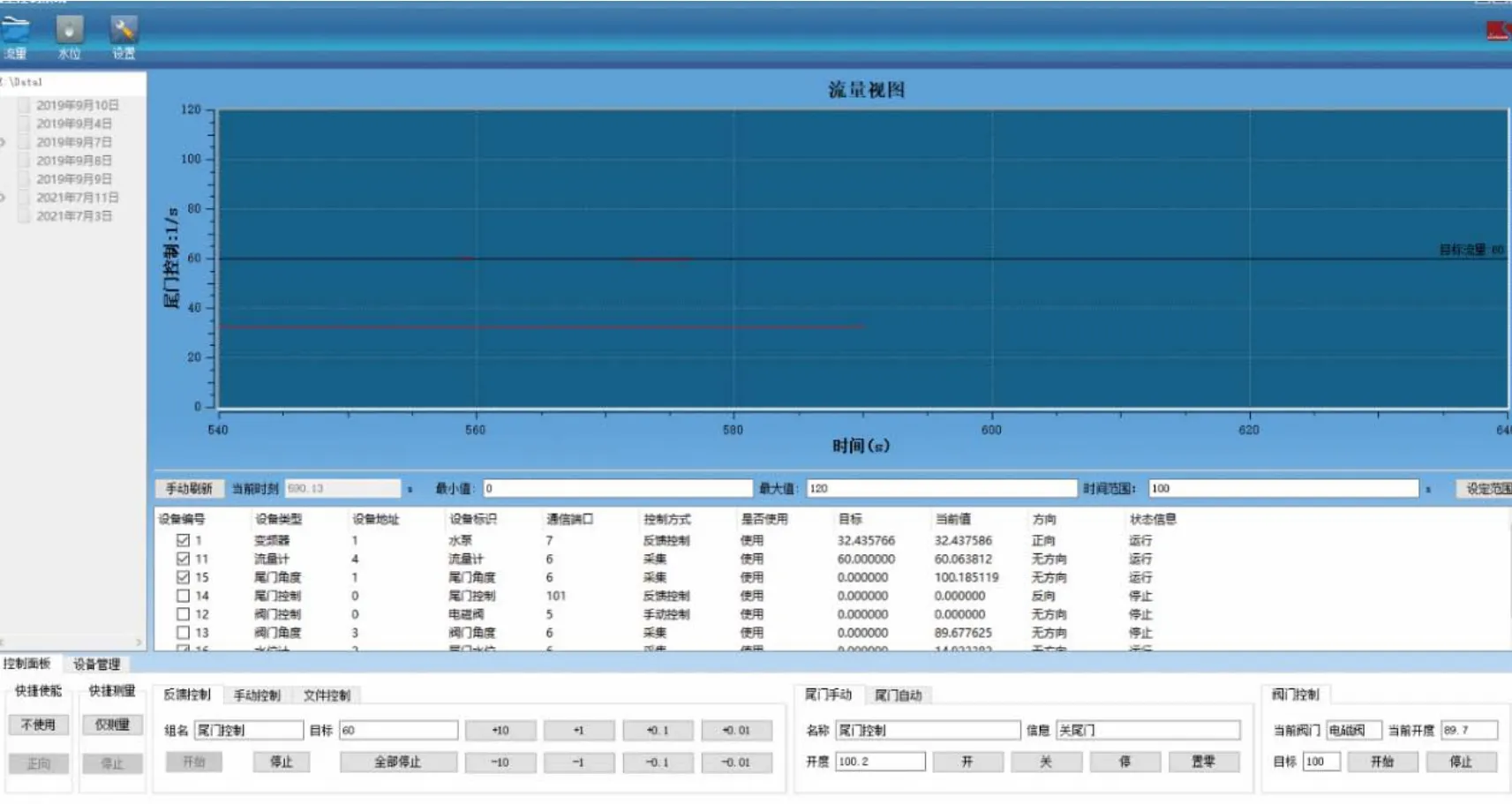
图5 流量控制系统Fig.5 Flow control system

图6 超声波水位计Fig.6 Ultrasonic water level gauge

图7 雷达水位计Fig.7 Radar water level gauge

图8 多普勒流速仪Fig.8 Doppler current meter

图9 变坡控制系统Fig.9 Slope control system

图10 网格划分示意图Fig.10 Schematic diagram of grid division

泥沙试验参考玛纳斯河多年平均含沙量2.2 kg∕m3［14］，试验用沙取自玛纳斯河天然河沙，根据流量的不同，在稳水池倾倒不同重量的河沙，搅拌均匀，具体试验泥沙重量，泥沙粒径级配分别如表2、表3所示。

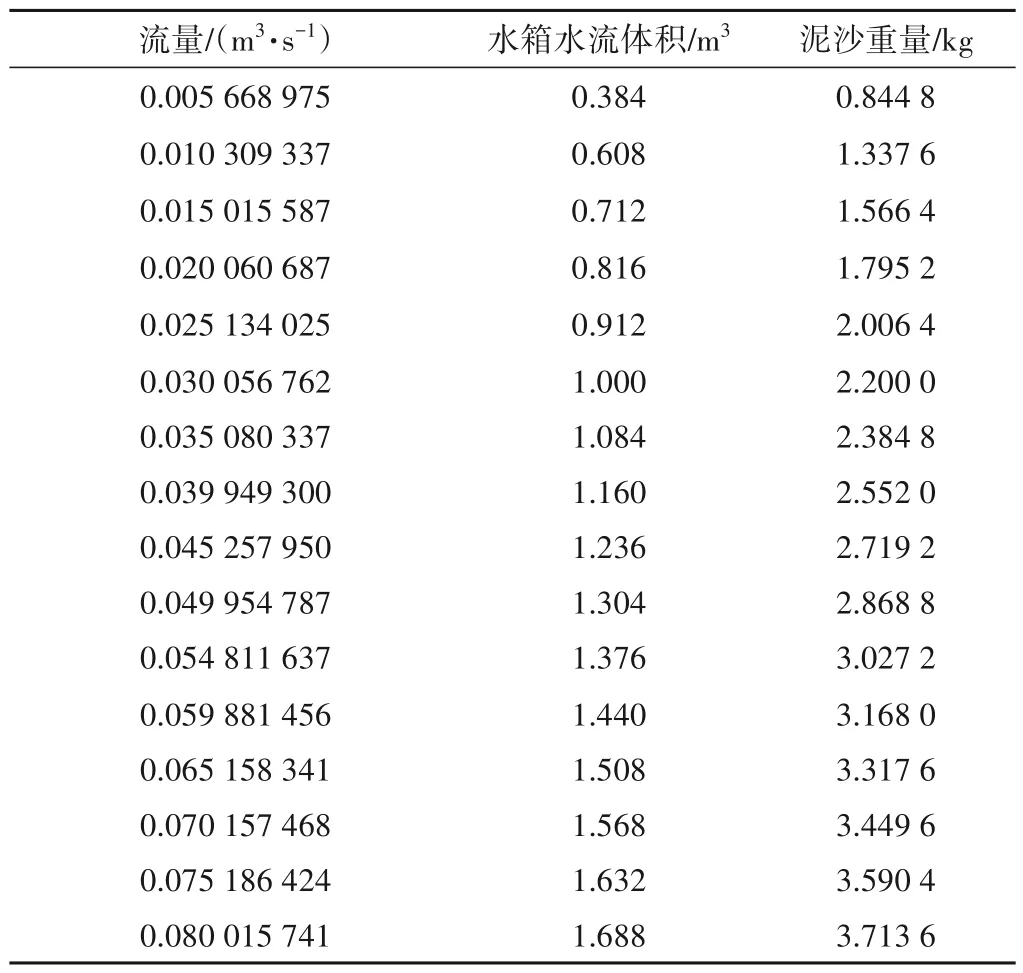
表2 不同流量下试验泥沙倾倒量Tab.2 Test sediment dumping under different flow rates

表3 天然河沙粒径级配Tab.3 Grain size grading of natural river sand

2 数值模拟方法

2.1 控制方程

多相流模型采用欧拉模型，欧拉模型允许对多个独立但相互作用的模型进行建模。这些相可以是任何组合的液体、气体或固体。每个相位的处理均使用欧拉法。欧拉模型适用于水沙两相流的固液滑移流动模拟。它将主相和次相均看作为一个连续相，通过压力和相间交换系数实现耦合。流体—固体流动间的交换模型采用Wen and Yu 模型，该模型适用于次相体积浓度明显低于主相的情况［15］。

2.2 体积分数方程

体积分数表示每个相所占的空间，每个相分别满足质量和动量守恒定律。

相位的体积Vq由以下公式定义［16］：

其中：

相q的有效密度表达式为：

式中：ρq为相q的物理密度。

2.3 质量守恒连续性方程

2.4 动量守恒方程

式中：μq和λq分别为相的剪切和体积黏度；为外部体积力；为浮托力；为虚拟质量力；为相之间的相互作用力；→Fwl，q为壁面滑移力；为湍流扩散力；为相间速度；Kpq为相间交换系数；p为两相间共享的压力。

2.5 网格划分

结构化网格具有计算效率高，但几何适应性差的特点。而非结构化网格，几何适应性较好，但计算较慢［17］。经过两者权衡，梯形和矩形渠道采用结构化网格，U形渠道采用结构化和非结构化网格的混合。网格质量较好，均在0.8 以上，满足计算精度要求。同时加密气液交界处网格数量，提高对液面捕捉的精度。梯形、矩形、U形网格数量分别为127万、105万、138万。

2.6 数值求解方法与边界条件

湍流方程采用RNGk-ε双方程模型［18，19］，算法采用基于压力耦合的coupled 算法。使用瞬态算法，时间步长为0.001 s。边界条件具体设置如图11 所示，自由表面边界采用压力进口，水相和沙相采用速度进口，沙相占0.014 67，壁面采用标准无滑移壁面，材质为钢，出口为充分发展的自由出流。

图11 边界条件示意图Fig.11 Schematic diagram of boundary conditions

3 结果与分析

3.1 模型验证

为验证模型可靠性，将59.881 456 L∕s流量0.1%坡度下3种渠道巴歇尔槽水位及流速的试验值与模拟值进行对比。如图12～15 所示，梯形渠道、U 形渠道、矩形渠道巴歇尔槽上游测点水位的试验与模拟相对误差分别为3.90%、1.31%、4.23%，最大误差不超过5%。由水面线可知，巴歇尔槽在收缩段为缓流，流经喉道段，水流由缓流经临界流转变成急流，数值模拟结果符合试验量水槽流态。梯形渠道、U形渠道、矩形渠道巴歇尔槽上游测点流速的试验与模拟相对误差分别为1.94%、0.82%、2.08%，最大误差不超过3%。即认为该模型满足模拟精度要求。

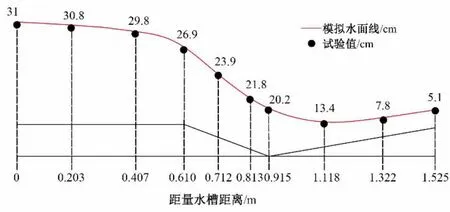
图12 梯形渠道巴歇尔槽水面线数值模拟与试验对比图Fig.12 Comparison between numerical simulation and test of water surface profile of trapezoidal channel and Parshall flume

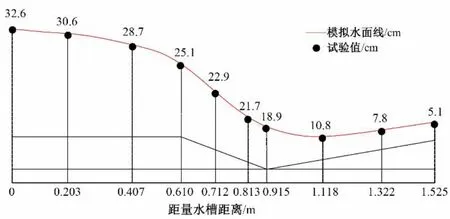
图13 U形渠道巴歇尔槽水面线数值模拟与试验对比图Fig.13 Comparison between numerical simulation and test of water surface profile of U-shaped channel and Parshall flume

图14 矩形渠道巴歇尔槽水面线数值模拟与试验对比图Fig.14 Comparison between numerical simulation and test of water surface profile of rectangular channel and Parshall flume

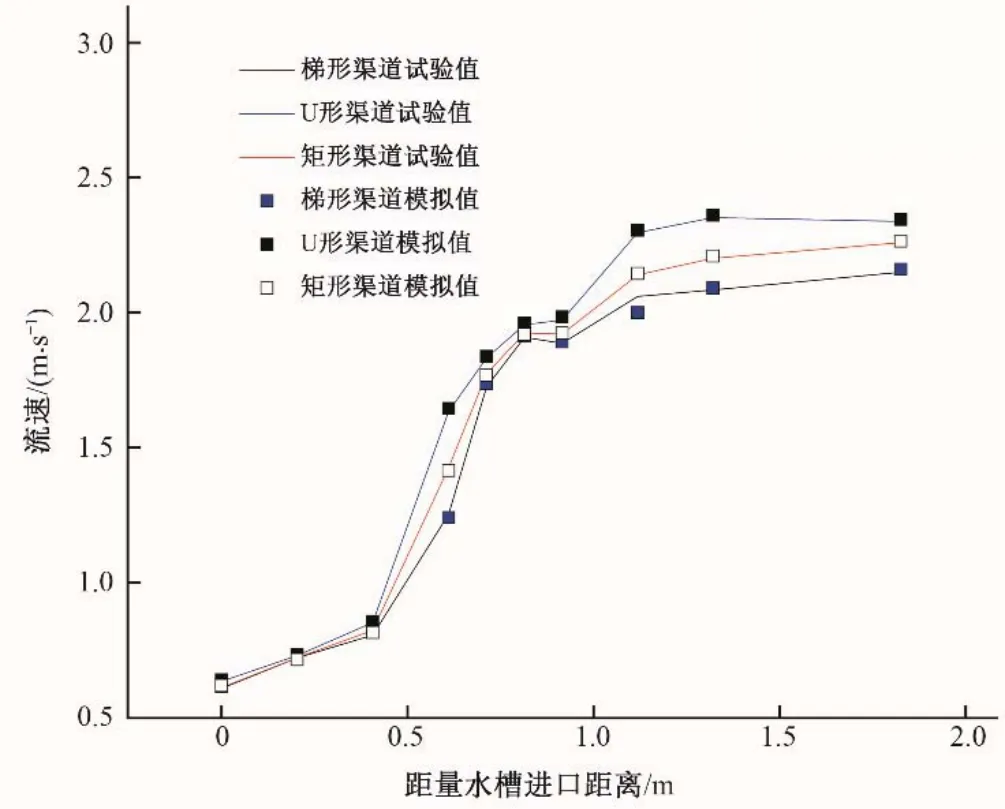
图15 3种渠道巴歇尔槽流速数值模拟值与试验对比图Fig.15 Comparison of numerical simulation values and test results of flow velocity in three channels

3.2 泥沙分布

图16 为59.881 456 L∕s 流量下3 种渠道巴歇尔槽分别在坡度0.1%、0.4%、0.8%的泥沙分布模拟图。图16中T、U、J分别表示梯形渠道、U 形渠道、矩形渠道。1、4、8 分别表示坡度0.1%、0.4%、0.8%。由图16 中可知梯形渠道泥沙相对集中在渠道上游与巴歇尔槽连接段底部两侧及下游渠道底部两侧，U 形渠道泥沙相对集中在渠道上游中间底部、巴歇尔槽上游连接段及渠道下游中间底部，矩形渠道泥沙分布相对比较分散。从整体来看3种渠道泥沙分布主要位于巴歇尔槽上游连接段位置。而在3 种渠道巴歇尔槽槽身泥沙分布中，梯形渠道巴歇尔槽泥沙积累最少，U形渠道巴歇尔槽泥沙积累最多。随着坡度的增加，渠道及巴歇尔槽泥沙含量开始逐渐减少，淤积程度逐渐降低。

图16 59.881 456 L/s流量下3种渠道各坡度巴歇尔槽泥沙分布模拟图Fig.16 Simulation diagram of sediment distribution in Parshall flume of three channels at the flow rate of 59.881 456 L/s

3.3 测流精度

由于本试验均是在自由出流情况下进行，根据《JJG（水利）004-2015 明渠堰槽流量计计量检定规程》，巴歇尔槽为单一的水位流量关系，其流量计算公式如下［12］：

式中：Q为流量，m3∕s；h为上游实测水头，m。

3 种渠道巴歇尔槽在0.1%～0.8%坡度下各流量的测流相对误差如图17 所示。总体来讲，3 种渠道巴歇尔槽的测流误差为：U形渠道＞矩形渠道＞梯形渠道。随着坡度的增加，测流误差逐渐增大；随着流量的增大，测流误差逐渐减小。在小流量5.668 975 L∕s时，3种渠道在0.1%坡度～0.3%坡度测流误差呈下降趋势，在0.3%坡度～0.8%坡度测流误差呈上升趋势。在0.02～0.04 m3∕s时，巴歇尔槽测流误差下降较为明显。0.02～0.04 m3∕s 对应的巴歇尔槽水位为15.5～24 cm，而巴歇尔槽的测量水位范围为3～45 cm，即在巴歇尔槽最大测量水位的34.44%～53.33%时，巴歇尔槽的测流误差下降较快，而超过53.33%后，测流误差下降较慢，最后曲线趋于平稳，测流相对稳定，误差较小。5.668 975 L∕s 对应的巴歇尔槽水深为6.97 cm，即当巴歇尔槽的水位小于最大测量水位的15.49%时，测流误差相对较大。3 种渠道在0.1%～0.4%坡度下的测流误差相对较小，大部分在规范规定的5%以内。而在0.4%～0.8%坡度下的测流误差相对较大，大部分工况逐渐超出5%。

图17 0.1%～0.8%坡度下各流量3种渠道巴歇尔槽测流相对误差Fig.17 The relative error of flow measurement in three channels with 0.1% ～ 0.8% gradient

3.4 流速分布

图18 为沿渠道方向各断面的位置示意图，断面1～14 的相对位置分别为0，1.5，3，3.2，3.403，3.606，3.81，3.912，4.014，4.115，4.318，4.521，5.025，6.325m。其中4～6为巴歇尔槽收缩段断面，7～9 为喉道段断面，10～12 为扩散段断面。分析各个断面的平均流速，得出如图17 所示的各断面沿Z方向的流速变化图。图19所示分别为流量5.668 975、59.881 456 L∕s下3种渠道0.1%～0.8%坡度的流速变化。在小流量5.668 975 L∕s下，3种渠道流速相近，巴歇尔槽流速在喉道段前1∕3处（即断面8处）达到最大值，由于流量较小，水流在扩散段流速较小，导致水流在喉道段末雍水，流速骤降，且泥沙易淤积在喉道末与扩散段的连接处，对上游收缩段流速有一定影响，这也是低流量下测流不准的原因之一。在大流量59.881 456 L∕s 下，3 种渠道流速相差较大，巴歇尔槽的流速最大值发生在扩散段，由于流量较大，水流冲刷较大，在喉道末处雍水现象减弱。从总体来看，随着坡度的增加，流速逐渐增大。在0.1%坡度～0.4%坡度下，3种渠道巴歇尔槽的流速差距相对不大，而坡度超过0.4%后，流速差距增加，U 形渠道＞矩形渠道＞梯形渠道，流态越来越急，临界流发生位置提前，导致槽内流速波动加剧，泥沙颗粒碰撞加剧，测流精度降低。

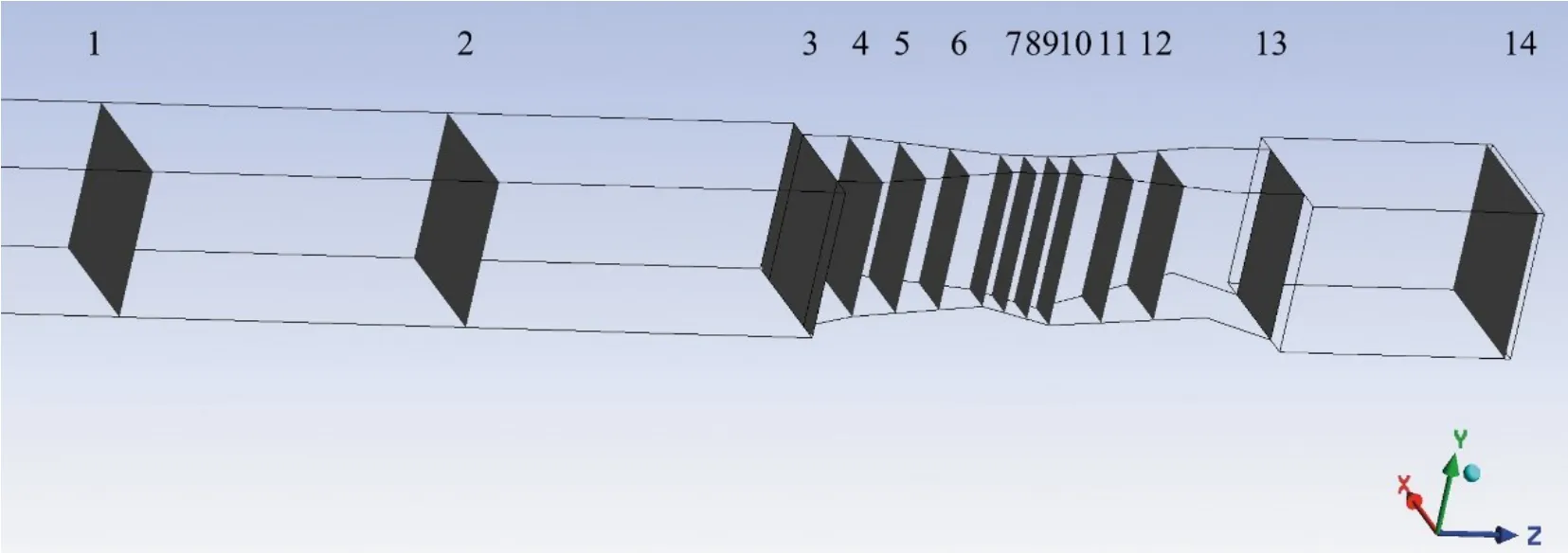
图18 断面位置图Fig.18 Section location map

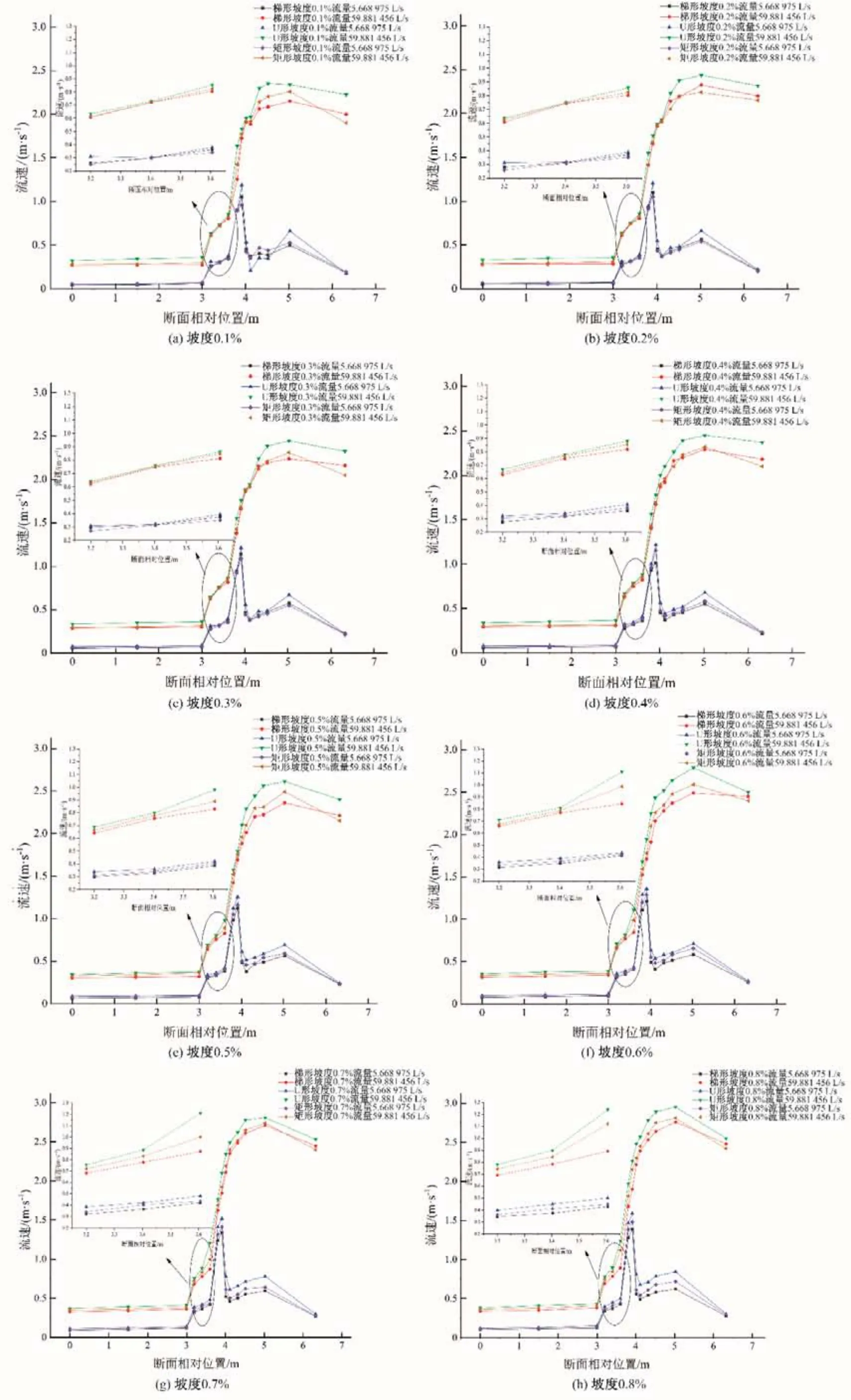
图19 5.668 975及59.881 456 L/s流量下沿渠道方向各断面流速分布Fig.19 Velocity distribution of each section along the channel under the flow of 5.668 975 and 59.881 456 L/s

3.5 挟沙能力

1958 年，张瑞瑾［20］等根据悬移质具有制紊作用的观点，从挟沙水流的能量平衡原理出发，建立能量平衡方程，导出了水流挟沙能力公式的结构形式：

式中：S*是悬移质水流挟沙能力，kg∕m3；U为断面平均流速，m∕s；R为水力半径，m，对于宽浅河道R可近似用断面平均水深h代替；ω为泥沙沉降速度，m∕s；g为重力加速度，m∕s2；K和m分别为水流挟沙能力系数和指数，这些系数可以通过半理论表达式和实测资料确定［21］，K取0.02，m取0.92。

此公式适用于含沙量0.1～100 kg∕m3［18］，其中悬移质泥沙粒径不大于0.062 mm时，沉速采用斯托克斯公式［20］：

式中：γs为泥沙的干容重，N∕m3；γ为水的容重，N∕m3；d取泥沙的中值粒径，m；v为运动黏滞系数，m2∕s。

当粒径为0.062～2.0 mm 时，采用沙玉清的过渡区沉速公式间接推算泥沙颗粒的沉降粒径：

式中：Sa为沉速判数；φ为粒径判数；ρs为泥沙密度，g∕cm3，ρω为清水密度，g∕cm3；ω沉降速度，cm∕s；d为中值粒径，mm；g为重力加速度，cm∕s2；ν为黏滞系数，cm2∕s。

图20、图21 分别为0.1%坡度，流量5.668 975、59.881 456 L∕s下断面1～14的沿程挟沙力图。由图中可知，5.668 975 L∕s流量下巴歇尔槽的最大挟沙力位于喉道段前1∕3处（断面8），最大值为0.28 kg∕m3；巴歇尔槽最小挟沙力位于扩散段进口处（断面10），最小值为0.006 kg∕m3。59.881 456 L∕s 流量下巴歇尔槽最大挟沙力位于扩散段后1∕3 处（断面13），最大值为6.04 kg∕m3；巴歇尔槽最小挟沙力位于巴歇尔槽进口，最小值为0.69 kg∕m3。流量越大，挟沙力越大。在大流量的情况下，巴歇尔槽大部分部位的挟沙力均大于2.2 kg∕m3，说明巴歇尔槽在大流量情况下，不存在淤积现象。

图20 5.668 975 L/s流量0.1%坡度挟沙力沿程分布图Fig.20 5.668 975 L/s flow 0.1% slope sediment carrying capacity along the road

图21 59.881 456 L/s流量0.1%坡度挟沙力沿程分布图Fig.21 59.881 456 L/s flow 0.1% slope sediment carrying capacity along the road

4 讨 论

通过计算流体动力学——CFD 对3 种渠道上巴歇尔槽0.1%～0.8%坡度的水沙试验进行了数值模拟。通过研究发现，欧拉模型对水沙模拟具有较高的拟合性，更加贴近实际情况，能够满足精度要求。相较于DPM 模型、混合模型，欧拉模型将所有相都看作连续相，且相与相之间互相耦合作用。而DPM 模型，将颗粒看作离散相，相与相之间的交互作用较弱，不适用于河流泥沙模拟。混合模型相当于简化了多相流，虽然其具有计算较快，收敛较快的特点，但是对于复杂流动，精度较低。

对于巴歇尔槽的研究，本文弥补了前人对巴歇尔槽泥沙及不同坡度不同渠道下研究的缺失。研究发现，梯形渠道在泥沙情况下具有较高精度。分析是由于梯形渠道将大部分泥沙拦截在巴歇尔槽上游连接段，且梯形渠道泥沙集中在渠底两侧，对水流影响较小，水与沙的掺互较少，对水流的扰动较小。而U形渠道泥沙集中在中间底部，泥沙易排放于巴歇尔槽，对测流精度有一定影响，为含沙量比较高的灌区提供了理论依据。同时，巴歇尔槽的修建应该在0.1%～0.4%坡度之间，坡度过大，对巴歇尔槽内水流的流态，流速均会产生影响，水位处于不稳定状态。在设计流量时，易将流量设计在巴歇尔槽最大测量水位的30%以上，能够保证测流精度。

但对于不同粒径的泥沙还有待进一步试验与分析，缺少巴歇尔槽对不同粒径泥沙的过流能力分析，作者将继续后续的研究。

5 结 论

（1） 在泥沙情况下，梯形渠道的巴歇尔槽具有更高的测流精度和适应性，槽身泥沙淤积较少。

（2） 0.1%～0.4%坡度下的巴歇尔槽能够较好满足测流精度，超过0.4%坡度后测流误差逐渐增大。

（3） 在巴歇尔槽最大测量水位的34.44%～53.33%时，巴歇尔槽的测流误差下降较快，而超过53.33%后，测流误差下降较慢，最后曲线趋于平稳，测流相对稳定，误差较小。建议在实践设计中，巴歇尔槽的水位保持在最大水位的30%以上。

（4） 为减少巴歇尔槽上游泥沙淤积，可适当提高渠道坡度，但建议不超过0.4%。