氯离子侵蚀环境中衬砌管片服役寿命的贝叶斯动态评估
邢科航, 冯现大, 卢 彬, 鲁 瑞
(济南大学 土木建筑学院, 山东 济南 250022)
随着城市建设的快速发展,隧道建设数量突飞猛进,给隧道的运营、维护带来了很大挑战。隧道运营时间的增加使得多数隧道因未及时养护而导致后期维护费用成倍增加[1]。服役隧道的耐久性评估理论及衬砌管片寿命预测是目前盾构隧道可靠度研究的重点。
盾构隧道设计的使用寿命一般为100 a[2],但是受衬砌管片工作环境的影响,空气中的氯离子、碳离子、硫酸根离子等进入钢筋混凝土内部,使钢筋发生锈蚀,导致衬砌管片提前丧失承载能力,不能达到设计规定使用年限[3]。很多研究[4-8]针对上述影响因素,基于可靠度理论对隧道进行寿命评估,但是多数研究认为,钢筋开始锈蚀时间即为衬砌管片寿命的终点,即当氯离子侵蚀深度达到保护层厚度时,认为衬砌管片失效。由于衬砌管片承载力还未达到极限,因此结果通常过于保守。
在隧道寿命预测方面,大多数研究[9-11]基于衬砌管片当前状态推断未来几十年甚至100 a的状况,忽略了衬砌管片性能随时间的变化。严格来讲,服役衬砌管片的抗力和荷载效应具有不确定性,使得衬砌管片性能劣化规律极其复杂,结果也具有一定的随机性。本文中利用正态分布模拟衬砌管片保护层厚度的随机性,考虑时变状态下混凝土抗压强度与钢筋抗拉强度变化,基于现有观测数据,通过贝叶斯理论完成对理论数据的更新,实现衬砌管片服役寿命的动态评估。
1 时变状态下衬砌管片侵蚀机制
大量工程实例[12-15]表明,钢筋锈蚀引起的混凝土开裂是混凝土结构劣化的主要原因。Collepardi等[16]提出用Fick第二定律描述氯离子在混凝土中的扩散现象,即
(1)
式中:w(x,t)为扩散时间是t时距混凝土表面距离为x处氯离子质量分数;w0为混凝土内初始氯离子质量分数;ws为结构表面氯离子质量分数;fe为误差函数;Dt为扩散时间是t时氯离子的扩散系数。
在Fick第二定律中, 假定扩散系数是恒定不变的, 与真实情况不符, 许多学者通过试验对Fick第二定律中氯离子扩散系数进行修正[17]。 万小梅[18]综合考虑混凝土的水化龄期、 暴露环境参数以及极限应力, 建立氯离子扩散系数模型, 但是在计算中考虑的因素仅与环境类因素有关。 Yu等[19]研究氯离子扩散系数随时间的变化, 并考虑了氯离子在多维空间中的扩散, 对扩散系数中的常数进行修正。 陈宣东等[20]通过建立氯离子扩散理论模型和随机骨料模型, 利用蒙特卡罗法模拟2 000个数值样本, 考虑混凝土的孔隙率、 氯离子活化能等, 根据模拟数据建立氯离子扩散系数模型。 余红发等[21]考虑氯离子扩散系数、 扩散系数随时间的依赖性以及混凝土结合氯离子的能力等, 建立了综合氯离子结合能力、 养护龄期、 混凝土结构缺陷影响的氯离子扩散系数模型。 该模型理论计算结果与实际观测结果十分接近, 得到很多学者的一致肯定[22], 本文中后续计算时采用余红发等[21]建立的氯离子扩散系数模型, 即
(2)
式中:H为混凝土内氯离子扩散性能的劣化效应系数;D0为初始氯离子扩散系数;R为混凝土结合氯离子的能力;Q为常数,一般取为0.64;t0为混凝土养护时间,取为28 d。
当氯离子浓度超过一定范围后,导致钢筋表面钝化膜破坏,钢筋开始锈蚀。关于钢筋锈蚀时钢筋表面氯离子临界值,国内外学者进行了大量试验研究[23-26],得到了钢筋开始锈蚀时表面氯化物限值,即氯化物质量占水泥质量的分数为0.2%~1.2%[26],差异较大。
氯离子与钢筋发生化学反应,使钢筋锈蚀,可通过计算钢筋锈蚀电流速率进而根据法拉第定理求出。钢筋锈蚀电流速率[27]为
(3)
式中:icorr(t)为扩散时间是t时钢筋锈蚀电流速率;W为水与水泥的质量比;T为热力学温度;Hr为相对湿度。
时变状态下钢筋的锈蚀深度[28]为
(4)
式中:xcorr(t)为扩散时间是t时钢材总量在径向的锈蚀深度;tint为氯离子到达钢筋表面的时间;Rcorr为锈蚀参数,当锈蚀类型为均匀锈蚀时取为1,当锈蚀类型为点锈蚀时取值范围为(2, 4)。
随着氯离子侵蚀的累积,钢筋有效截面面积产生变化,进而影响钢筋抗拉强度。当氯离子未到达钢筋表面时,忽略钢筋抗拉强度的变化;当氯离子到达钢筋表面时,认为氯离子与钢筋发生作用,钢筋抗拉强度产生变化的求解公式[29]为
(5)
式中:fs(t)为扩散时间是t时锈蚀钢筋的抗拉强度;fs0为未锈蚀钢筋的名义抗拉强度;η(t)为扩散时间是t时钢筋截面损失率。
混凝土抗压强度是影响衬砌管片承载力的一个重要因素,但在荷载、环境、时间等的影响下,混凝土抗压强度随时间先增大,然后逐渐减小。牛荻涛等[30]的试验结果表明,经过时间t的混凝土抗压强度仍服从正态分布。混凝土抗压强度的均值和标准差分别为
(6)
式中:μ(t)为扩散时间是t时混凝土抗压强度的均值;μ为混凝土28 d抗压强度的均值;σ(t)为扩散时间是t时混凝土抗压强度的标准差;σ为混凝土28 d抗压强度的标准差。
韩兴博等[31]建立了衬砌管片的抗弯承载力计算模型。为了简化计算,本文中衬砌管片的抗弯承载力计算公式[32]为
(7)
式中:M(t)为扩散时间是t时衬砌管片承载力;fcu(t)为扩散时间是t时混凝土抗压强度;b为衬砌截面宽度;ha为衬砌混凝土受压区高度;h0为衬砌截面有效高度;As为衬砌受压区钢筋有效截面面积;as为受压区混凝土边缘到钢筋外边缘距离。
2 服役隧道衬砌管片可靠度计算
蒙特卡罗法可将参数作为随机变量输入,从而以概率的方式对可靠度进行输出,通过选择合适的抽样次数N,即可得到所需要的精度。结构的时变极限状态方程为
Z(t)=R(t)-S(t),
(8)
式中:Z(t)为扩散时间是t时结构的极限状态函数;R(t)为扩散时间是t时结构的抗力;S(t)为扩散时间是t时管片的效应。
蒙特卡罗法计算t时刻衬砌管片劣化概率的流程如图1所示。

X1, X2,…, Xj—参与计算衬砌管片承载力因子的均值、方差等特征参数, j=1, 2,; i—抽样次数,i=1, 2,, N;Nf—失效次数,初始值为0; M(t)—扩散时间是t时衬砌管片承载力;[M]—衬砌管片极限承载力,[·]为设计标准值;P—衬砌管片承载力的失效概率。图1 蒙特卡罗法计算t时刻衬砌管片劣化概率的流程
本文中利用Python软件生成随机数,将保护层厚度、混凝土抗压强度、钢筋抗拉强度作为随机变量输入,验算衬砌管片承载力是否满足衬砌管片极限承载力[M]([·]为设计标准值)的要求,最后输出衬砌管片承载力劣化概率P,将概率转换成可靠度即可。抽样次数N以计算所求精度为准[33]。
3 衬砌管片服役寿命动态评估
贝叶斯理论是关于条件概率的命题,在贝叶斯动态更新中,当有新的数据可用时,可以基于先验信息的数据的初始分布,从而获得后验分布[34]。目前贝叶斯动态评估已被广泛使用[35-36]。
以概率密度函数表示连续随机变量的贝叶斯公式[37]为
(9)
式中:π(θ∣z)为给定事件z发生后事件θ发生的条件概率密度函数;f(z∣θ)为给定事件θ后事件z发生的条件概率密度函数;π(θ)为事件θ发生的先验分布概率密度函数。
1、 2节中所述氯离子侵蚀、 衬砌管片承载力计算模型均为理论计算模型, 输入的计算参数多为确定值。 实际上, 衬砌管片在地下受到多种随机性较强的因素的影响, 导致计算结果与真实值有一定的偏差。 衬砌管片服役寿命的贝叶斯动态评估过程如图2所示。 假设当前时刻为t2, 需要进行更新的特征因子为J, 则更新步骤如下:1)对理论数据进行整理。通过概率论理论求得J在t2时的特征参数, 假设因子的分布类型, 并计算J的概率密度函数。 2)对J在t2时的观测数据进行统计分析, 假设观测数据的分布类型, 并计算观测数据的概率密度函数,计算f(z∣θ)。 3)根据式(9)计算J更新后的概率密度函数,并计算均值和标准差,完成在t2时对J的更新。后续可多次加入观测数据,实现对隧道寿命的动态评估,利用贝叶斯公式使理论与观测数据相结合,实现对理论计算数据的更新,达到对既有隧道结构体系的动态评估。

[M]—衬砌管片极限承载力, [·]为设计标准值;t1—钢筋开始锈蚀时间; t2、t3—加入观测数据的时刻;[t]—理论计算隧道寿命; tu—贝叶斯动态评估后隧道寿命。图2 衬砌管片服役寿命的贝叶斯动态评估过程
当需要更新的特征参数D的模拟与观测数据均服从正态分布且标准差已知时,贝叶斯更新后的均值和标准差[35]分别为
(10)
(11)
式中:μD、σD为贝叶斯更新后特征参数D的均值和标准差;μD1、σD1为特征参数D发生的先验分布的均值和标准差;μD2、σD2为加入观测数据后特征参数D的均值和标准差。
4 算例分析
以某盾构隧道工程为例,混凝土强度等级为C50,衬砌管片及环境参数如表1所示。该隧道在运营30 a后,隧道内30个衬砌管片材料样本的参数观测数据如表2所示。

表1 某盾构隧道的衬砌管片及环境参数

表2 某盾构隧道内30个衬砌管片材料样本的参数观测数据
4.1 考虑保护层厚度不确定的氯离子浓度理论计算与模拟计算
由于保守估计氯离子到达钢筋表面作为衬砌管片寿命终点,因此为了对比理论计算的可靠性,同时考虑衬砌管片保护层厚度服从正态分布,进行106次蒙特卡罗数值模拟,计算氯离子侵蚀概率,氯离子浓度理论计算与蒙特卡罗模拟计算结果如图3所示。由图可知:在隧道运营起初的10 a,钢筋表面氯离子浓度增加较快,随着时间的推移,氯离子浓度增加明显放缓; 在第37年, 钢筋表面处氯化物质量占水泥质量的分数达到临界值0.69%, 模拟计算与理论计算结果保持一致, 认为衬砌管片内钢筋已受到氯离子侵蚀。

图3 氯离子浓度理论计算与蒙特卡罗模拟计算结果
在实际中,氯离子侵入并不会导致隧道寿命结束,但此时衬砌管片材料中钢筋随着氯离子的侵蚀导致锈蚀,通过蒙特卡罗模拟将混凝土抗压强度与钢筋抗拉强度作为随机变量,考虑到2个随机变量随时间的变化服从正态分布,蒙特卡罗模拟计算的混凝土抗压强度与钢筋抗拉强度的正态分布如图4所示。将混凝土抗压强度与钢筋抗拉强度代入衬砌管片承载力计算公式,计算衬砌管片承载力的失效概率及可靠度。

(a)第20年
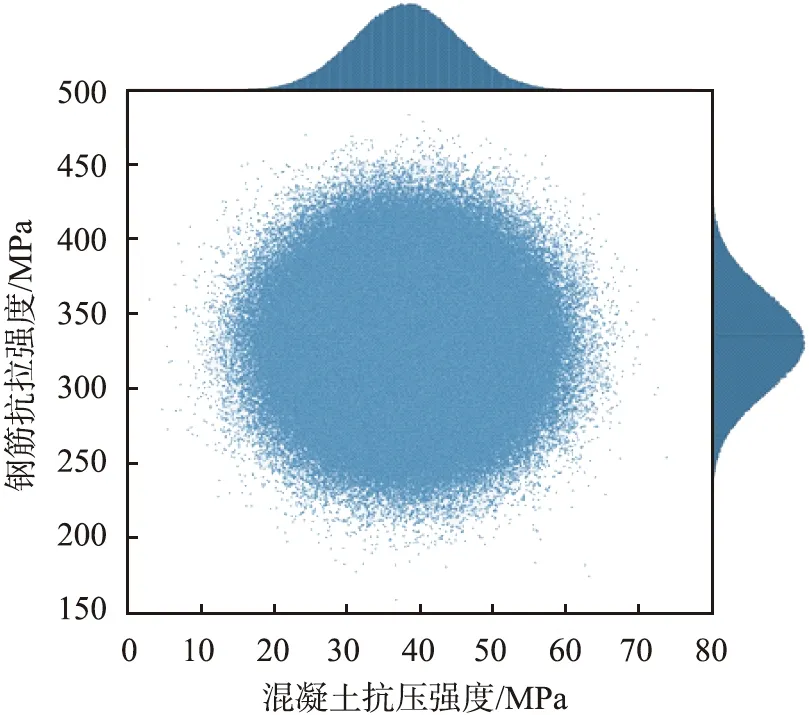
(b)第80年图4 蒙特卡罗模拟计算的混凝土抗压强度与钢筋抗拉强度的正态分布
通过理论计算衬砌管片承载力,考虑到混凝土抗压强度和钢筋屈服强度服从正态分布,通过106次蒙特卡罗模拟,计算衬砌管片承载力,考虑部分钢筋锈蚀。衬砌管片失效概率与可靠度计算结果如图5所示。由图可知:在第37年,氯离子侵蚀导致衬砌混凝土内钢筋发生锈蚀,此时衬砌管片失效概率开始增大,管片可靠度也发生了大幅变化; 在第92年,管片承载力可靠度低于设定目标值1.5,认为此时隧道破坏且隧道寿命为92 a,隧道寿命提前失效。
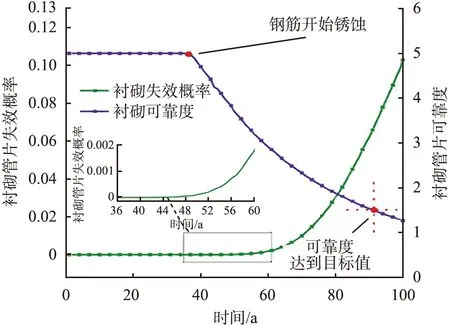
图5 衬砌管片失效概率与可靠度计算结果
4.2 基于观测数据的衬砌管片承载力分析
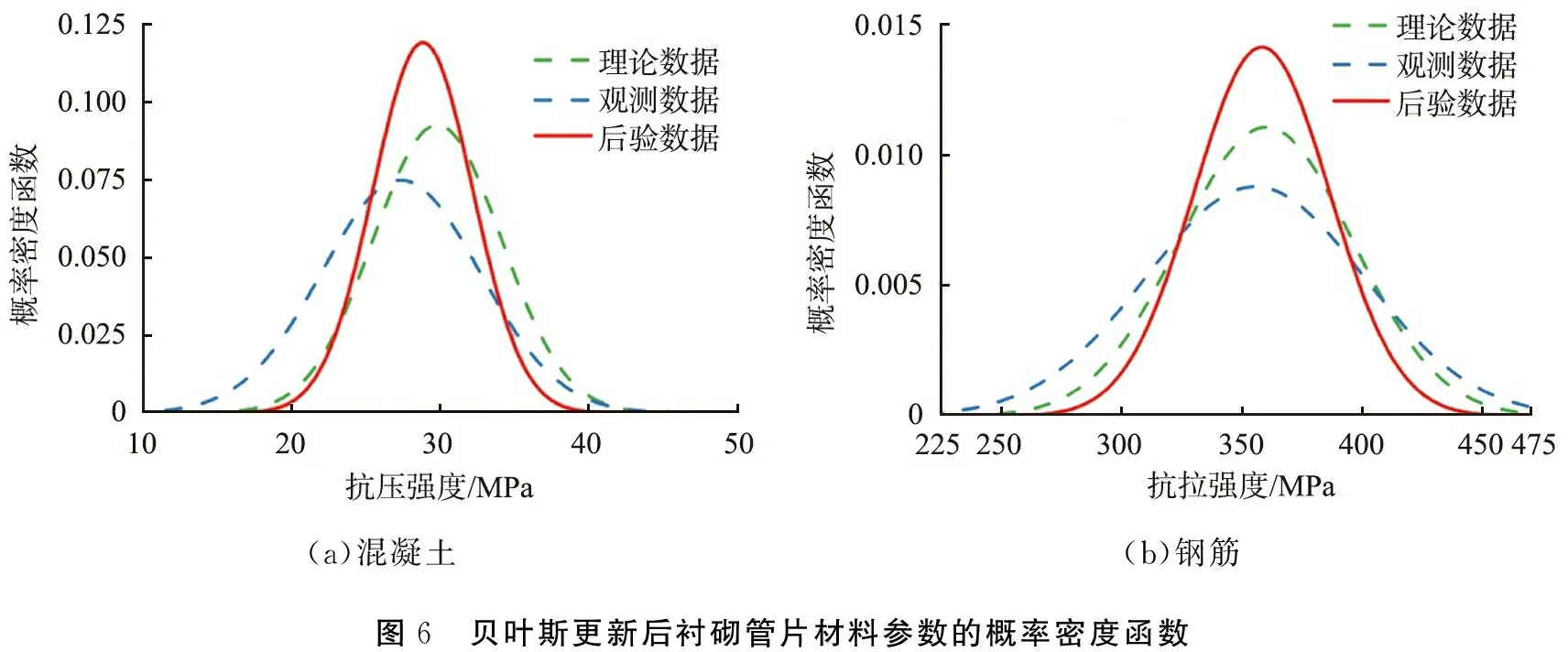
由于地下环境具有不确定性,因此无法仅通过单一确定性参数对隧道寿命进行预测。为了得到隧道寿命较真实的表现,可通过加入观测数据实现对现有参数的更新。为了便于后续计算,假设现有混凝土实测抗压强度和钢筋实测抗拉强度值均服从正态分布,某盾构隧道的实测数据与模拟计算数据如表3所示。由表可知,实测样本数据与模拟数据偏差较大,如果以模拟计算数据进行寿命预测,则预测结果过于保守。为了得到隧道寿命较为真实的表现,通过贝叶斯公式进行模拟数据的更新。贝叶斯更新后衬砌管片材料参数的概率密度函数如图6所示。

表3 某盾构隧道的实测数据与模拟计算数据
利用蒙特卡罗法对更新后的混凝土抗压强度与钢筋抗拉强度进行重新采样,并计算衬砌管片承载力,贝叶斯更新后第30年混凝土抗压强度与钢筋抗拉强度的正态分布如图7所示,贝叶斯更新后衬砌管片可靠度如图8所示。由图可知:在进行隧道寿命更新后,隧道可靠度提前失效。在第88年,衬砌管片可靠度提前达到目标值,较未进行更新提前4%;由于衬砌管片可靠度提前失效, 隧道提早宣告破坏, 因此,为了确保隧道的安全,必须采取有效的措施改善隧道内衬砌的可靠性,并进行有效的监测和维护。

图7 贝叶斯更新后第30年混凝土抗压强度与钢筋抗拉强度的正态分布

图8 贝叶斯更新后衬砌管片可靠度
5 结论
本文中考虑时变状态下氯离子侵蚀钢筋影响衬砌管片承载力的劣化机制,利用衬砌管片当前性能预测未来衬砌管片承载力的变化,实现了对服役衬砌管片承载力劣化评价的全过程描述,以及对服役衬砌管片结构性能的精确把控,得到的主要结论如下:
1)当仅考虑氯离子到达钢筋表面作为衬砌管片寿命终点时,理论计算与模拟计算结果保持一致,隧道使用寿命为37 a。
2)在氯离子侵入衬砌管片后, 管片的承载力发生了显著变化, 当以可靠度为基准时, 衬砌管片在第92年因可靠度不足而失效, 此时隧道的使用寿命为92 a。
3)通过理论数据与观测数据实现对衬砌管片结构性能的预测, 将已有数据通过贝叶斯公式对理论计算数据进行更新, 重新计算管片可靠度; 结果显示, 在第88年, 管片可靠度达到目标值, 此时隧道的寿命为88 a, 提前4%; 为了保护隧道的安全使用, 需要提前做好维护措施, 以确保隧道能够达到设定年限。
影响钢筋锈蚀的因素很多,本文中仅考虑氯离子对衬砌管片造成侵蚀,并未考虑隧道内碳离子等对衬砌管片内侧受拉侧钢筋的影响,另外,在考虑氯离子对环境影响时,计算参数也应随隧道所处环境而变化。在利用贝叶斯更新时,可针对多种参数进行更新计算。本文中仅对混凝土抗压强度和钢筋抗拉强度进行更新且仅更新1次,后续可长期并通过多次观测数据对衬砌管片承载力进行更新,实现对隧道安全更好的预测。上述问题在后续研究中需要进一步完善。

