基于水准仪钢尺高程传递法的精度分析

笪凤齐

摘要 水准测量、三角高程测量和目前应用广泛的GPS高程测量是高程测量常用的方法，其中水准测量主要适用于平坦地区，施测及数据处理简单，精度、可靠性最高，是目前最主要的方法。水准测量的不足之处是当已知点与待定点距离较远时，费时费力，效率较低。三角高程测量法比水准测量法速度快、效率高，但由于其受外界因素影响较大，精度和稳定性难以保证。文章通过实验对水准仪联合钢尺高程传递的方法进行了精度分析，结果表明这种方法精度高、可靠性好，具有较高的应用价值。

关键词 高程测量；建筑工程测量；精度分析

中图分类号 TB22文献标识码 A文章编号 2096-8949（2023）12-0108-03

0 引言

高程测量常用的方法有水准测量、三角高程测量和目前应用广泛的GPS高程测量。上述方法中，水准测量施测及数据处理简单，精度和可靠性最高，是目前最常用的方法。其不足之处是当已知点与待定点距离较远时，费时费力，效率较低；三角高程测量法比水准测量法速度快，效率高，但由于其受外界因素影响较大，精度和稳定性难以保证[1-4]，当满足一定条件可代替三、四等水准测量，在特定情况下甚至可代替一等、二等水准测量[5-6]。GPS高程测量获得的直接观测值是待定点的大地高，只有获得其高程异常值后才可转换为正常高。高精度的高程异常值获取常见的方法有高程拟合和内插已有的高精度似大地水准面，其中高程拟合受到拟合点高程精度、拟合点点数、拟合点与待定点之间距离等因素的影响[7-10]，在现行的工程测量规范中认为其只可代替五等水准测量[11]，且需满足一定条件要求。内插高精度水准面的方法的前提是施测区域内已有高精度的似大地水准面产品，且待定点需获得高精度的大地高，在全国的大部分地区，由于受到经济条件的影响而没有施测高精度的似大地水准面，故采用该法较为困难，所以GPS高程测量法受到较多条件的制约有待进一步发展。

在一些特殊的场合，如基坑、桥墩、桥台和建筑物等施工过程中，经常需要将高精度高程引测到基坑底部、桥墩、桥台上或建筑物顶部，由于高差较大，无法采用水准测量或者进行水准测量十分困难，甚至有时无法采用三角高程和GPS测量方法进行施测，此时采用水准仪联合钢尺法进行高程传递较为方便。由于对于该方法精度的研究或文献较少，采用该方法施测的精度究竟如何，针对此问题，该文通过实验的方法进行了探讨。

1 水准测量原理和误差分析

1.1 水准测量原理

水准测量是利用水准仪提供的水平视线，借助水准尺求得两点的高差。根据测得的高差和已知点的高程，推算未知点高程。为求出A、B两点的高差hAB，在A、B两个点上竖立水准尺，在A、B两点之间安置水准仪。当视线水平时，在A、B两个点的标尺上分别读得读数a和b，则hAB等于两个标尺读数之差。a是已知高程点上的水准尺读数，称为“后视读数”；b是在未知高程点上的水准尺读数，称为“前视读数”。高差是后视读数减去前视读数。高差值是正表示未知点B高于已知点A，高差值是负表示未知点B低于已知点A。此外，测量由A向B进行，高差用hAB表示；反之由B向A进行，高差用hBA表示，二者大小相等，符号相反。

hAB=a?b （1）

如果A点高程已知，则B点的高程：

HB=HA+hAB （2）

若安置一次仪器，需观测多个点高程，可采用视线高法，如图1所示，Hi為水平视线高程：

Hi=HA+a=HB+b （3）

故HB=Hi?b （4）

1.2 水准测量误差分析

水准测量误差主要来源于仪器误差、观测误差和外界自然条件3个方面。

1.2.1 仪器误差

（1）残余误差。水准仪的主要轴线是视准轴CC、水准管轴LL、仪器竖轴VV及圆水准器轴L?L?。各轴线间应满足L?L?∥VV，十字丝横丝垂直于竖轴和LL∥CC。由于仪器长期使用和运输中的震动等原因，上述各轴线间关系会发生变化，故仪器使用前应检验校正。仪器虽经检验校正，但不可能十分完善，会有一定的残余误差。残余误差一般是系统误差，采用正确的方法可以消除或减弱。如水准管轴和视准轴不平行所引起的i角误差，可通过观测时前后视距相等的方式消除或减弱。

（2）水准尺误差。水准尺误差主要有水准尺分划不准、水准尺零点误差及尺身弯曲变形等。水准尺必须经过检验才能使用，对于零点误差可通过两根水准尺交替使用，当每一测段测站数为偶数，即可消除该项误差。

1.2.2 观测误差

观测误差中的整平误差是指仪器水平时水准管气泡未严格居中，水准仪未提供一条水平视线，从而引起的误差。水准尺的估读毫米位误差与水准尺基本分划、望远镜放大倍率和视距有关。由于视差的存在，未精确瞄准水准尺并使读数产生误差。水准尺立尺时应竖直。若水准尺倾斜，其读数总比竖直时读数大，视线越高，水准尺倾斜引起的读数误差越大。读数时可采用“摇尺法”，即立尺者缓慢前后俯仰摇动水准尺，读数缓慢变化，当观测员读取最小读数时，即为立尺竖直时的读数。

1.2.3 外界环境

（1）仪器和尺垫下沉。由于仪器下沉，使视线降低，从而引起高差误差。如果转点尺垫下沉，将使下一站后视读数增大。所以仪器和转点位置应坚硬稳定，观测时间应尽量缩短，或采用“后—前—前—后”的观测程序减弱误差影响。

（2）地球曲率和大气折光。用水平面代替大地水准面时，没有考虑地球曲率影响，水准尺上读数产生的误差为c，称为球差。如式（6），式中D为测站至测点距离，R为地球半径。

地面的空气温度不均匀，所以空气的密度也不均匀。光线在密度不匀的介质中沿曲线传布，被称为“大气折光”。白天近地面的空气温度高，密度低，弯曲的光线凹面向上；晚上近地面的空气温度低，密度高，弯曲的光线凹面向下。由于空气的温度在不同时刻和不同地方一直处于变动之中，所以很难描述折光的规律。由于大气折光，视线并非水平，而是一条曲线，其折光量的大小对水准读数产生的影响为r，称为气差，如式（7）所示。大气折光与地球曲率的影响称为球气两差，用f表示，如式（8）所示：

1.2.4 温度与风力

温度会引起仪器的部件胀缩，视准轴的构件（物镜、十字丝和调焦镜）相对位置会产生变化，或者视准轴相对水准管轴位置产生变化。不均匀的温度对仪器的性能影响尤其大，气泡会朝着温度高的方向移动，影响仪器整平，产生误差，故观测时应注意撑伞遮阳。温度的变化也会引起大气折光的变化。大风可使水准尺竖立不直，影响水准管气泡的稳定性。

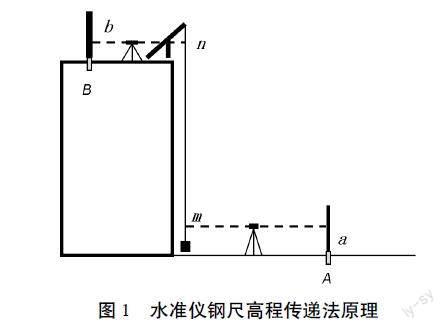
2 水准仪钢尺高程传递法原理

如图1所示，A为桥墩附近地面已知水准点，B为桥墩顶部的待定水准点。在桥墩顶悬挂一把钢尺，尺端朝下，底端悬挂一垂锤并置于一盛满油的水桶，以拉直钢尺，防止悬吊的钢尺受风力等因素影响晃动而影响观测读数。

分别在A、B竖立水准尺，在钢尺与桥墩上、下的标尺之间各安置一台水准仪，照准水准尺读数分别为a1、b1；然后地面和桥墩顶部的水准仪同时照准钢尺，读数分别为m、n（同时读数可避免钢尺移动所产生的误差），并测定地面和桥墩顶的气温；最后再次照准A、B处的水准标尺，读数a2、b2。两次标尺读数的平均值为a、b。则A、B两点的高差如[12]式（9）：

式中，Δl——钢尺改正数，Δld——尺长改正数；Δlt——温度改正数；ΔlN——张力误差改正数；——因钢尺重力引起的误差改正数，即：

其中，温度改正：Δlt=（n?m）×α×（t?20），式中：t——观测时刻实测温度，α——钢尺的线膨胀系数，若观测采用的是标准拉力（即重锤重力扣除其在水中的浮力后正好等于钢尺的标准拉力时），此项改正数为0，钢尺重力引起的误差极小可略去，则A、B两点间的高差公式hAB如式（11）所示：

移动钢尺吊架，以桥墩顶部B点作为后视，重复上述观测，得返测高差hBA。若hAB与hBA之差（较差）在规定限差内，取其平均值作为最终结果。

3 实验精度分析

该次试验使用的仪器包括Trimble DINI12型数字水准仪2台，其标称精度为每1 km往返测高差中误差0.3 mm；50 m精密钢尺1把，其膨胀系数为0.000 011 5，标准拉力100 N；标称精度为0.1 ℃的温度计2只；特制重锤1个（扣除其在水中的浮力后其重力正好为钢尺的标准拉力）；钢支架一个。观测前对全部仪器进行鉴定，各项指标满足实验要求。

我们在三栋不同高度的建筑物楼下和楼顶分别设置2个水准标志，分别为A1、A2、A3和B1、B2、B3，首先按照三等水准测量要求分别对建筑物上下两个点间进行水准观测，观测成果如表1所示。

从表1可以看出，观测的结果满足三等水准测量的要求，由此获得建筑物上、下两点间的水准高差，再按照水准仪联合钢尺进行高程传递方法的原理进行高程测量，观测中若往测高差与返测高差较差小于0.5 mm时取均值作为最终观测结果，否则应重新测量。对观测结果进行尺长、温度改正后获得最终结果（由于采用标准拉力以及因钢尺重力引起的误差较小，此两项改正略去），实验成果如表2所示。

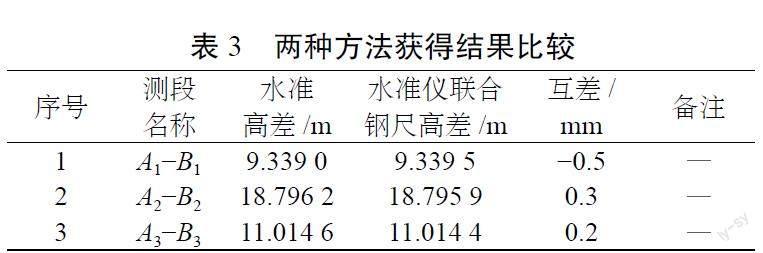
两种方法获得的结果的比较如表3所示。

从表3我们可以看出，两种方法获得的高差非常接近，水准仪联合钢尺进行高程传递的方法与水准测量方法获得结果的精度相当，且可靠性好。

4 结论

根据水准测量法和水准仪联合钢尺法两种方法实施过程比较，可以得出以下结论：

（1）水准测量法观测简单，计算方便；后者观测时过程复杂，且需要测定温度和拉力测量，并进行相应改正，计算过程繁琐。

（2）水准测量法观测需要沿楼梯一站一站地进行观测，在狭窄的楼梯间进行观测非常困难，有时甚至难以实现；后者一般可一次传递观测完成，特殊情况时还可分段传递完成。

（3）水准测量法在楼层较高时观测误差累计较大；后者在楼层较高时受到钢尺长度的限制，且楼层较高时受到风力温度影响也较大，观测精度较差。

（4）一般情况下，水准仪联合钢尺法的效率较前者高。

通过以上实验表明，水准仪联合钢尺进行高程传递的方法精度高、可靠性好，与水准测量、三角高程测量和GPS高程测量相比，在基坑、桥墩和建筑物等类似特殊应用现场具有较高的应用价值。

参考文献

[1]郭宗河， 郑进凤. 电磁波测距三角高程测量公式误差的研究[J]. 测绘通报， 2004（7）： 12-13.

[2]潘松庆， 章书寿. 根据气温变化率进行三角高程测量的折光改正[J]. 河海大学学报（自然科学版）， 1999（5）： 12-16.

[3]许国辉. 高精度EDM三角高程测量的研究[J]. 测绘通报， 2002（10）： 22-24.

[4]姜晨光. 精密三角高程测量严密计算的理论研究与初步实验[J]. 四川测绘， 1996（3）： 125-128.

[5]张正禄， 邓勇， 罗长林， 等. 精密三角高程代替一等水准测量的研究[J]. 武汉大学学报（信息版）， 2006（1）： 5-8.

[6]周水渠. 精密三角高程测量代替二等水准测量的尝试[J]. 测绘信息与工程， 1999（3）： 25-29.

[7]张兴福. 刘成， 王兵海， 等. 无水准数据的GPS高程转换方法及精度分析[J]. 大地测量与地球动力学， 2010（2）： 114-118.

[8]李征航GPS测高精度的研究[J]. 武汉测绘科技大学学报， 1993（3）： 67-73.

[9]郭革新， 赫建忠. GPS测高的局限性与可能性评述[J]. 全球定位系統， 2000（3）： 30-32.

[10]高伟， 徐绍铨GPS高程分区拟合转换正常高的研究[J]. 武汉大学学报（信息科学版）， 2004（10）： 908-911.

[11]工程测量规范： GB50026—2007[S]. 北京：中国计划出版社， 2008.

[12]张正禄. 吴栋才， 杨仁. 精密工程测量[M]. 北京：测绘出版社， 1993.