基于TiO2忆阻器的混沌系统研究
韩旭 陈诚 徐佳敏 曲信儒 黄庆南 余志强
摘 要:将基于离子漂移模型建立的TiO2忆阻器作为非线性模块,设计一个可以产生独特吸引子的忆阻混沌系统。首先通过水热法工艺制作纳米忆阻器件,并分析该忆阻器的电学特性。其次对器件的电学特性进行拟合,采用离子漂移模型建立Au/TiO2/FTO忆阻器的数学模型,令模型产生的电流电压(I-U)曲线与收集到的Au/TiO2/FTO忆阻器电学特性数据相吻合。为了说明该忆阻模型的有效性,改变施加在模型两侧的电压信号频率,发现忆阻模型I-U曲线滞回面积减小,当频率增加到50 Hz左右时曲线趋向一条直线,仿真结果表明该模型符合忆阻器的特性。最后设计了基于忆阻器的混沌电路,将忆阻模型与电容电感串联形成MLC电路,调整电路中的电感值参数大小,令系统进入混沌状态,产生混沌吸引子。为了分析系统动力学特性,绘制混沌系统分岔图,发现不同参数值会令电路系统在混沌态与周期态之间转换,根据系统分岔图改变参数,说明吸引子阐述的系统状态与分岔图阐述的状态基本一致。采用复杂忆阻模型设计混沌系统,研究结果为忆阻混沌系统的发展提供实验基础。
关键词:忆阻器;Au/TiO2/FTO;混沌电路;混沌吸引子
中图分类号:TM13 DOI:10.16375/j.cnki.cn45-1395/t.2023.03.012
0 引言
近年来关于神经网络[1-2]的研究热度越来越高,但是神经网络由于需要庞大的计算力而对硬件要求越来越高,故急需一种可以代替传统存储单元的器件。Chua等[3]提出一种新型电路元件模型,并将其命名为忆阻器。随着对忆阻器研究的深入,研究人员发现基于忆阻器的神经网络可以更好地模拟人脑的神经系统,于是研究人员基于忆阻器对神经网络的稳定性[4]、准确性[5-6]、运算速率性能[7]和图像处理应用[8]等方面进行研究,并取得一定成果。基于忆阻器的混沌系统[9-14]也广受人们关注,忆阻器的混沌电路因其能产生无法预测的混沌序列的特點,在图像加密[15-17]方面有较优的效果。
自忆阻器提出以来,人们设计出了各种不同器件结构的二元氧化物忆阻器。Strukov 等[18]制作出真实物理器件后,研究人员开始研究制作方法和材料对忆阻器性能的影响。Dongale等[19]通过水热法制作Ag/TiO2/Al忆阻器,阐述了该忆阻器的元素组成和开关阻变机制,但是制作出的忆阻器高低阻态开关比只在一个数量级左右。Swathi等[20]通过磁控溅射法制作Al/HfOx/FTO忆阻器,并通过退火提高了忆阻器开关比,说明退火在特定条件下可以改善忆阻器性能。Prusakova 等[21]通过溶胶-凝胶和脉冲等离子体团簇源(PMCS)的方式制备TiO2薄膜,忆阻器开关比明显,电流为mA级别,且短路现象减少,改善了忆阻器性能,为忆阻器的商业化应用作了铺垫。Sun等[22]基于二维材料六方氮化硼(h-BN),首次报导了h-BN的液面自组装特性,成功应用于阻变存储研究领域,并在低成本微纳米制造领域[23]突破传统技术限制,为低成本忆阻器制备提供方向。Li等[24]改善了LED器件性能,证明了纳米结构对材料性能的影响。
此外,在忆阻器应用方面,混沌系统加入忆阻模型后表现出了更复杂的动力学行为。忆阻混沌系统产生的混沌系列具有无序性与不可预测性,根据这一特性,忆阻混沌系统在图像处理、加密及通讯方面有极高的应用价值。Yu等[25]基于蔡氏电路提出了一种利用3次绝对值方程替代非线性部分的系统,并对电路进行搭建,得到的结果与仿真一致。
目前,忆阻混沌系统中忆阻器模型大多较为简单,即忆阻模型中磁通量与电荷量呈现线性分段函数或简单光滑非线性函数等。此种忆阻模型优点是变化连续,模型简单,分析计算忆阻混沌系统的平衡点、特征方程及特征根等比较方便,但缺点是电学特性与真实物理器件不吻合,没有器件支撑。而基于离子漂移模型的忆阻模型电学特性与真实物理器件相吻合,此类忆阻混沌系统的雅可比矩阵及特征方程较为复杂,平衡点计算困难,相关报道罕见,但是系统可靠性和可行性高。本文基于水热法制备TiO2忆阻器,采用由惠普实验室提出的物理模型进行仿真,将忆阻模型、电容和电感进行串联,组成基于忆阻器的混沌电路,形成混沌吸引子,绘制分岔图等,阐述混沌系统的行为动力学。
1 TiO2忆阻器模型
1.1 Au/TiO2/FTO忆阻器电学特性分析
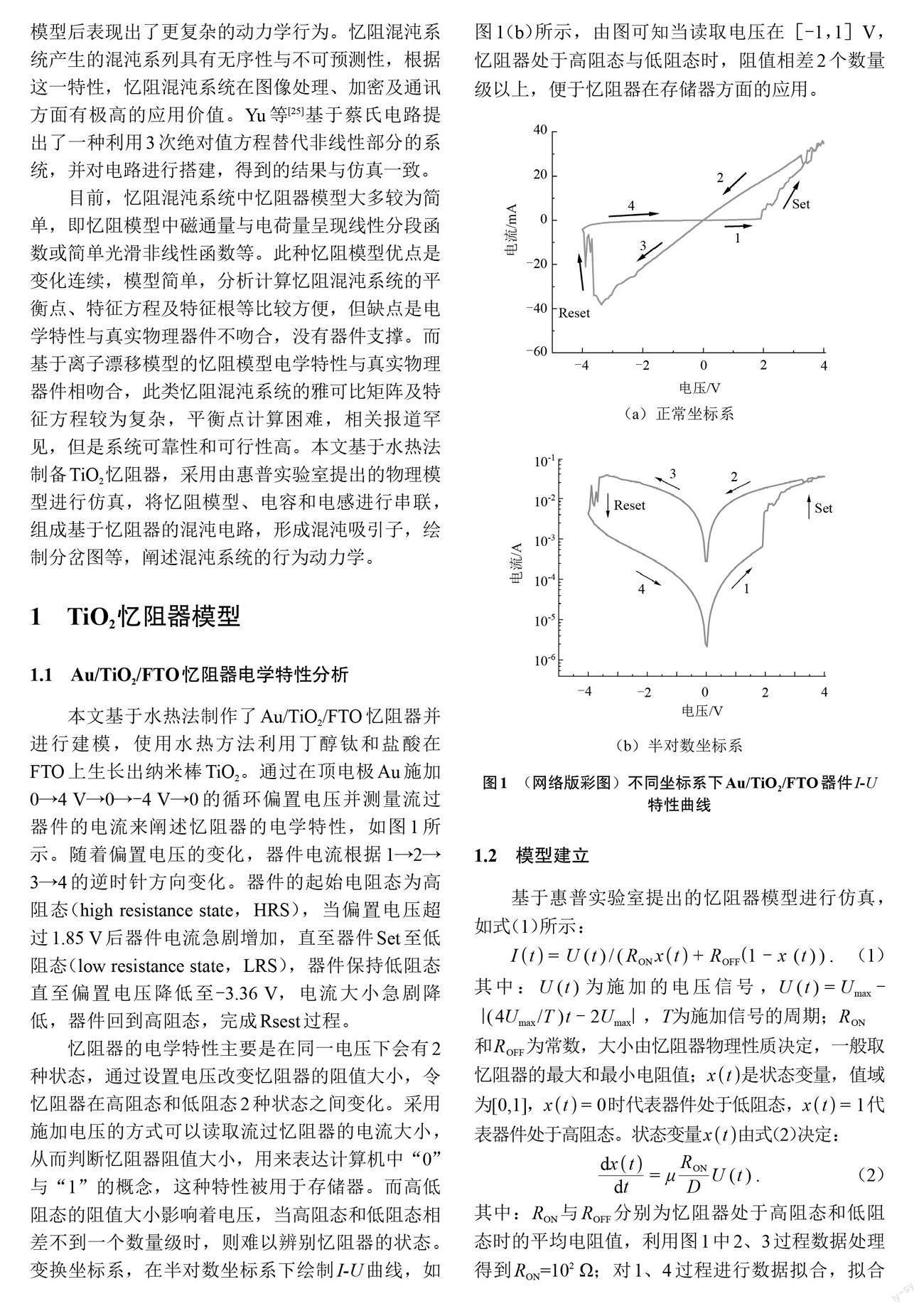
本文基于水热法制作了Au/TiO2/FTO忆阻器并进行建模,使用水热方法利用丁醇钛和盐酸在FTO上生长出纳米棒TiO2。通过在顶电极Au施加0→4 V→0→-4 V→0的循环偏置电压并测量流过器件的电流来阐述忆阻器的电学特性,如图1所示。随着偏置电压的变化,器件电流根据1→2→3→4的逆时针方向变化。器件的起始电阻态为高阻态(high resistance state,HRS),当偏置电压超过1.85 V后器件电流急剧增加,直至器件Set至低阻态(low resistance state,LRS),器件保持低阻态直至偏置电压降低至-3.36 V,电流大小急剧降低,器件回到高阻态,完成Rsest过程。
忆阻器的电学特性主要是在同一电压下会有2种状态,通过设置电压改变忆阻器的阻值大小,令忆阻器在高阻态和低阻态2种状态之间变化。采用施加电压的方式可以读取流过忆阻器的电流大小,从而判断忆阻器阻值大小,用来表达计算机中“0”与“1”的概念,这种特性被用于存储器。而高低阻态的阻值大小影响着电压,当高阻态和低阻态相差不到一个数量级时,则难以辨别忆阻器的状态。变换坐标系,在半对数坐标系下绘制I-U曲线,如图1(b)所示,由图可知当读取电压在[-1,1]V,忆阻器处于高阻态与低阻态时,阻值相差2个数量级以上,便于忆阻器在存储器方面的应用。
1.2 模型建立
基于惠普实验室提出的忆阻器模型进行仿真,如式(1)所示:
[It=U(t)/(RONxt+ROFF1-x(t)) . ](1)其中:[U(t)]为施加的电压信号[,U(t)=Umax-|(4Umax/T)t-2Umax|,T为施加信号的周期;RON]和[ROFF]为常数,大小由忆阻器物理性质决定,一般取忆阻器的最大和最小电阻值;[xt]是状态变量,值域为[0,1],[xt=0]时代表器件处于低阻态,[xt=1]代表器件处于高阻态。状态变量[xt]由式(2)决定:
[dxtdt=μRONDU(t) .] (2)
其中:RON与ROFF分别为忆阻器处于高阻态和低阻态时的平均电阻值,利用图1中2、3过程数据处理得到RON=102 Ω;对1、4过程进行数据拟合,拟合得到的直线斜率为ROFF=104 Ω;μ为离子迁移率[18],取值为μ=10-14 m2·s-1·V -1;D为半导体膜的厚度,通过场发射扫描电镜测量得到,取值为D=2×10-6 m;Umax为测量忆阻器时施加的三角波电压信号参数,取值为Umax=4 V;T=30 s。
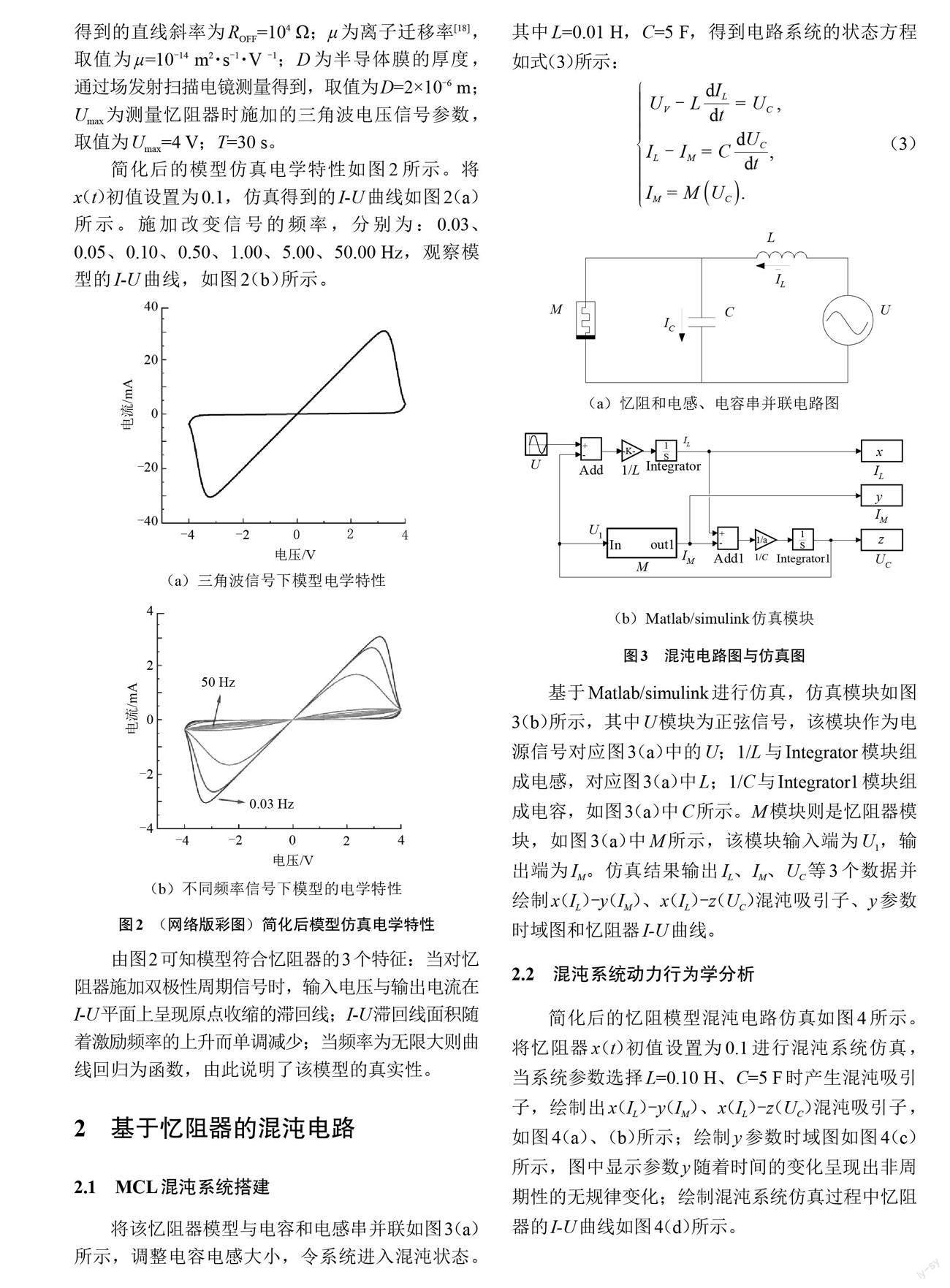
简化后的模型仿真电学特性如图2所示。将x(t)初值设置为0.1,仿真得到的I-U曲线如图2(a)所示。施加改变信号的频率,分别为:0.03、0.05、0.10、0.50、1.00、5.00、50.00 Hz,观察模型的I-U曲线,如图2(b)所示。
由图2可知模型符合忆阻器的3个特征:当对忆阻器施加双极性周期信号时,输入电压与输出电流在I-U平面上呈现原点收缩的滞回线;I-U滞回线面积随着激励频率的上升而单调减少;当频率为无限大则曲线回归为函数,由此说明了该模型的真实性。
2 基于忆阻器的混沌电路
2.1 MCL混沌系统搭建
将该忆阻器模型与电容和电感串并联如图3(a)所示,调整电容电感大小,令系统进入混沌状态。其中L=0.01 H,C=5 F,得到电路系统的状态方程如式(3)所示:
[UV-LdILdt=UC , IL-IM=CdUCdt,IM=MUC. ] (3)
基于[Matlab/simulink]进行仿真,仿真模块如图3(b)所示,其中U模块为正弦信号,该模块作为电源信号对应图3(a)中的U;1/L与Integrator模块组成电感,对应图3(a)中L;1/C与Integrator1模块组成电容,如图3(a)中C所示。M模块则是忆阻器模块,如图3(a)中M所示,该模块输入端为U1,输出端为IM。仿真结果输出IL、IM、UC等3个数据并绘制x(IL)-y(IM)、x(IL)-z(UC)混沌吸引子、y参数时域图和忆阻器I-U曲线。
2.2 混沌系统动力行为学分析
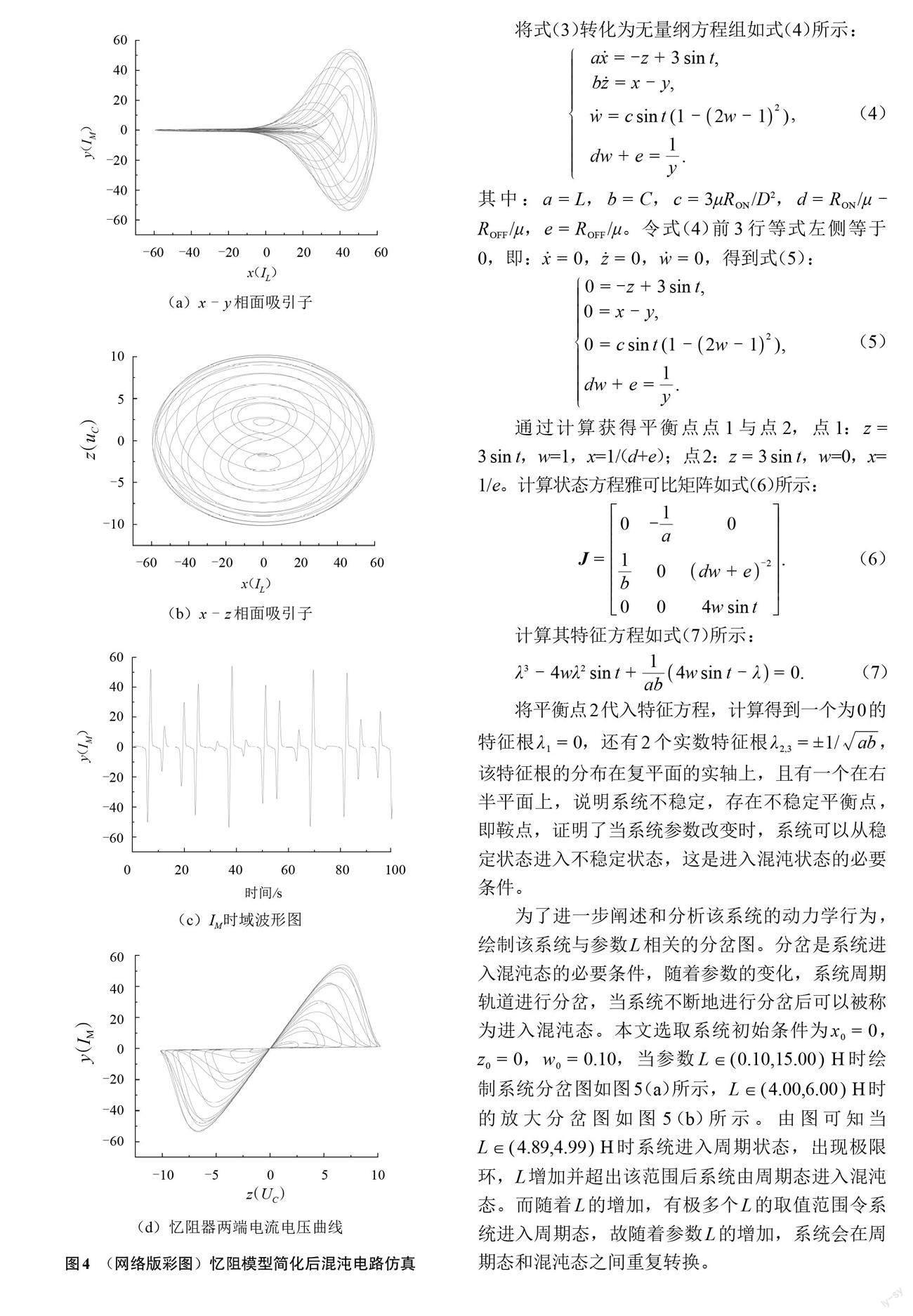
简化后的忆阻模型混沌电路仿真如图4所示。将忆阻器x(t)初值设置为0.1进行混沌系统仿真,当系统参数选择L=0.10 H、C=5 F时产生混沌吸引子,绘制出x(IL)-y(IM)、x(IL)-z(UC)混沌吸引子,如图4(a)、(b)所示;绘制y参数时域图如图4(c)所示,图中显示参数y随着时间的变化呈现出非周期性的无规律变化;绘制混沌系统仿真过程中忆阻器的I-U曲线如图4(d)所示。
将式(3)转化为无量纲方程组如式(4)所示:
[ax=-z+3sin t, bz=x-y, w=csint(1-2w-12)dw+e=1y. ,] (4)
其中:[a=L],[b=C],[c=3μRON/D2],[d=RON/μ-ROFF/μ],[e=ROFF/μ]。令式(4)前3行等式左侧等于0,即:[x=0],[z=0],[w=0],得到式(5):
[0=-z+3sin t, 0=x-y, 0=csint(1-2w-12), dw+e=1y. ] (5)
通过计算获得平衡点点1与点2,点1:[z=3sin t],w=1,x=1/(d+e);点2:[z=3sin t],w=0,x=1/e。计算状态方程雅可比矩阵如式(6)所示:
[J=0-1a01b0dw+e-2004w sint .] (6)
计算其特征方程如式(7)所示:
[λ3-4wλ2sint+1ab4wsin t-λ=0. (7)]
将平衡点2代入特征方程,计算得到一个为0的特征根[λ1=0],还有2个实数特征根[λ2,3=±1/ab],该特征根的分布在复平面的实轴上,且有一个在右半平面上,说明系統不稳定,存在不稳定平衡点,即鞍点,证明了当系统参数改变时,系统可以从稳定状态进入不稳定状态,这是进入混沌状态的必要条件。
为了进一步阐述和分析该系统的动力学行为,绘制该系统与参数L相关的分岔图。分岔是系统进入混沌态的必要条件,随着参数的变化,系统周期轨道进行分岔,当系统不断地进行分岔后可以被称为进入混沌态。本文选取系统初始条件为[x0=0],[z0=0],[w0=0.10],当参数[L∈(0.10,15.00)] H时绘制系统分岔图如图5(a)所示,[L∈(4.00,6.00)] H时的放大分岔图如图5(b)所示。由图可知当[L∈(4.89,4.99)] H时系统进入周期状态,出现极限环,L增加并超出该范围后系统由周期态进入混沌态。而随着L的增加,有极多个L的取值范围令系统进入周期态,故随着参数L的增加,系统会在周期态和混沌态之间重复转换。
为检测分岔图的正确性,查看不同范围内分岔图的状态,分别取[L]为4.94、5.00、9.00、11.10 H这4个不同的值。由图5(b)可知,当[L=4.94] H时系统进入2周期态,[L=5.00] H时系统进入混沌态;同理,当[L=9.00、11.10] H时系统进入周期态,混沌系统进入周期态时其吸引子收缩为极限环,故取[L=4.94、9.00、11.10] H时绘制吸引子相图,验证分岔图的正确性,同时取[L=5.00] H时验证系统是否进入混沌态。系统x-z平面投影如图6所示。由图6可知,L取4.94、9.00及11.00 H时系统进入周期态,当L取5.00 H时,系统为混沌状态,与上述分岔图分析完全一致,表明了实验结果的准确性。
3 结论
本文介绍了一种通过水热法制备的Au/TiO2/FTO忆阻器,测量该忆阻器I-U特性曲线,通过数据分析,拟合出I-U曲线的特征,并基于离子漂移模型理论,利用[Matlab]进行建模;模型建立完成后,通过改变施加在忆阻器模型的电压信号频率,观察模型的I-U曲线,发现从临界频率开始,随着激励频率的增加,忆阻器I-U滞回曲线的面积单调减小,并收缩至一个函数,说明该模型有效。此外,将该忆阻模型加入LC电路中,构成MLC电路,改变相关元件的参数大小令系统进入混沌,并通过混沌吸引子、分岔图等方式进行该系统的动力行为学分析。目前仅基于简单忆阻器模型进行混沌电路仿真,未来期望基于吻合真实物理器件I-U曲线的忆阻器模型设计混沌电路,提高电路的真实可靠性。
参考文献
[1] 刘敬敏,王文涛,夏雨.基于BP神经网络和一次二阶矩法的结构可靠度分析[J].广西科技大学学报,2023,34(1):36-42,72.
[2] 雷蕾,李健,吴青鸿.基于RBF神经网络自适应控制的下肢外骨骼步态跟踪[J].广西科技大学学报,2021,32(3):42-47,52.
[3] CHUA L O,KANG S M.Memristive devices and systems[J].Proceedings of the IEEE,1976,64(2):209-223.
[4] 王芬.基于憶阻器的随机神经网络的稳定性[J].工程数学学报,2022,39(4):522-532.
[5] 赵益波,蒋文,孟若禹,等.基于忆阻器卷积神经网络的表情识别[J].电子测量技术,2022,45(16):93-101.
[6] 武长春,周莆钧,王俊杰,等.基于忆阻器的脉冲神经网络硬件加速器架构设计[J].物理学报,2022,71(14):304-312.
[7] 王永甲,王瑞博,赵一阳,等.基于AgInSbTe忆阻器的高效MLP神经网络[J].信息技术,2022(1):1-5.
[8] 吴洁宁,闫登卫,王丽丹,等.基于忆阻器的细胞神经网络及在图像处理中的应用[J].西南师范大学学报(自然科学版),2022,47(3):1-8.
[9] XIE X D,ZOU L J,WEN S P,et al.A flux-controlled logarithmic memristor model and emulator[J].Circuits,Systems,and Signal Processing,2019,38(4):1452-1465.
[10] RAJAGOPAL K,ARUN S,KARTHIKEYAN A,et al.A hyperchaotic memristor system with exponential and discontinuous memductance function[J].AEU-International Journal of Electronics and Communication,2018,95:249-255.
[11] XU B R,WANG G Y,IU H H C,et al.A memristor-meminductor-based chaotic system with abundant dynamical behaviors[J].Nonlinear Dynamics, 2019,96(1):765-788.
[12] WU J,WANG G Y,IU H H C,et al.A nonvolatile fractional order memristor model and its complex dynamics[J].Entropy,2019,21(10):955.
[13] GUO Q,WANG N,ZHANG G S.A novel current-controlled memristor-based chaotic circuit[J].Integration,2021,80:20-28.
[14] WANG G Y,YUAN F,CHEN G R,et al. Coexisting multiple attractors and riddled basins of a memristive system[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2018,28(1):013125.
[15] 姚晓璐,张国有,王江帆,等.混沌加密的三维网格模型盲水印算法[J].计算机与现代化,2021(6):120-126.
[16] HAGRAS E A A,SABER M.Low power and high-speed FPGA implementation for 4D memristor chaotic system for image encryption[J].Multimedia Tools and Applications,2020,79(31-32):23203-23222.
[17] SUN J W,YANG Q F,WANG Y F.Dynamical analysis of novel memristor chaotic system and DNA encryption application[J].Iranian Journal of Science and Technology,Transactions of Electrical Engineering,2020,44(1):449-460.
[18] STRUKOV D B,SNIDER G S,STEWART D R,et al.The missing memristor found[J].Nature,2008,453(7191):80-83.
[19] DONGALE T D,SHINDE S S,KAMAT R K,et al.Nanostructured TiO2 thin film memristor using hydrothermal process[J].Journal of Alloys and Compounds,2014,593:267-270.
[20] SWATHI S P,ANGAPPANE S.Enhanced resistive switching performance of hafnium oxide-based devices:effects of growth and annealing temperatures[J].Journal of Alloys and Compounds,2022,913:165251.
[21] PRUSAKOVA V,GIUSTI G,COLLINI C,et al.Merging the sol-gel technique with the pulsed microplasma cluster source deposition to improve control over the memristive response of TiO2 thin films[J].Coatings,2021,11(3):348.
[22] SUN T Y,TU J,ZHOU Z P,et al.Resistive switching of self-assembly stacked h-BN polycrystal film[J].Cell Reports Physical Science,2022,3(7):100939.
[23] SUN T Y,LIU Y,TU J,et al.Wafer-scale high anti-reflective nano/micro hybrid interface structures via aluminum grain dependent self-organization[J].Materials & Design,2020,194:108960.
[24] LI H O,CAO L,FU T,et al.Morphology-dependent high antireflective surfaces via anodic aluminum oxide nanostructures[J].Applied Surface Science,2019,496:143697.
[25] YU S M,L? J H,CHEN G R.A module-based and unified approach to chaotic circuit design and its applications[J].International Journal of Bifurcation and Chaos,2007,17(5):1785-1800.
Study of chaotic system based on TiO2 memristor
HAN Xu1a, CHEN Cheng1a, XU Jiamin1a, QU Xinru1a, HUANG Qingnan1b, YU Zhiqiang*1a,2
(1a.School of Electronic Engineering, Guangxi University of Science and Technology, Liuzhou 545616, China;
1b.School of Automation, Guangxi University of Science and Technology, Liuzhou 545616, China;
2.Wuhan National Laboratory for Optoelectronics, School of Optical and Electronic Information,
Huazhong University of Science and Technology, Wuhan 430074, China)
Abstract: The TiO2 memristor based on the ion drift model is used as a nonlinear module to design a memristor chaotic system that can produce a unique attractor. Firstly, nanometer memristor devices are fabricated by hydrothermal process, and the electrical characteristics of the memristor are analyzed. Secondly, we fit the electrical characteristics of the device, establish the mathematical model of the Au/TiO2/FTO memristor by using the ion drift model, enabling the current voltage(I-U)curve generated by the model to fit well with the collected electrical characteristics data of Au/TiO2/FTO memristor. In order to illustrate the effectiveness of the memristor model, we change the frequency of the voltage signal applied on both sides of the model, it is found that the hysteresis area of the I-U curve of the memristor model is reduced, when the frequency increases to about 50 Hz, the curve tends to a straight line, the simulation results show that the model conforms to the characteristics of memristor. Finally, a chaotic circuit based on memristor is designed, the memristor model and the capacitor inductance are connected in series to form an MLC circuit. The inductance value parameters in the circuit are adjusted to make the system enter a chaotic state and generate a chaotic attractor. In order to analyze the dynamic characteristics of the system, we draw a bifurcation diagram of the chaotic system, it is found that different parameter values will make the circuit system convert between the chaotic state and the periodic state. The parameters are changed according to the system bifurcation diagram, it shows that the system state described by the attractor is basically consistent with the state described by the bifurcation diagram. The use of complex memristor models to design chaotic systems provides references for the study of memristor chaotic system.
Key words: memristor; Au/TiO2/FTO; chaotic circuit; chaotic attractor
(責任编辑:黎 娅)

