多核CPU环境下的并行KNN算法设计
潘峰 苏浩辀 段艳 闵云霄


关键词:并行KNN算法;多线程;二维数组;最佳近邻
0 引言
以数据驱动的机器学习,已成为当前处理大数据的主要技术,KNN 算法是机器学习中的主要算法之一。该算法应用很广,在机器学习中可用于回归、分类等监督学习,也可与遗传算法、粒子群优化算法等结合用于特征优化工作。KNN 算法简单易懂,不足之处是随数据规模的增加,其计算量也增大。为此,众多学者都尝试改进KNN 算法[1-5],提高KNN 算法的应用广度、速度及精度。文献[6,7]将KNN 算法与智能算法结合,用于进行特征选择;文献[8-13]对KNN 算法进行并行化,以此提高KNN 算法的速度;文献[14,15]通过数据集的约简来改进KNN 算法速度,文献[16,17]提出学习特征权重向量,增加KNN 算法的精度。
本文研究一种快速的并行KNN 算法,以该算法为评估特征权值向量的适度值函数,并通过演化计算,搜索最优的特征权值向量。由于适度值函数处理较为庞大的数据集时其计算速度成为群体演化计算的瓶颈,因此研究高速并行KNN 算法很有价值。
1 并行计算环境
在单核单线程的计算环境中只能实现并发,不能实现真正意义上的并行计算。当前个人电脑的体系结构已经发生重大变化,硬件主要是多核CPU 架构及核数更多的多核GPU,Java、Python 等軟件开发环境很容易构造并行程序[18,19],这为并行计算提供了可行性条件,本工作主要依托于多核CPU 环境使用Java 实现并行计算。
1.1 并行KNN 算法的思想
本文立足于现在的多核CPU 计算环境,利用Java软件开发环境设计多线程分解计算任务,将训练集分割为多个训练子集,每个线程独立地计算新数据在自己训练子集中的最近邻,主程序归并所有线程返回的最近邻,最终确定所有最近邻中的最佳近邻的类型为新数据类型。
1.2 KNN 分类问题的易并行性
一个问题的求解方案评估一般包含主要两个指标,一个是速度,另一个是精度,本工作的KNN 算法的并行化主要是解决速度的问题。分析易知,KNN 算法是易于实现并行化的算法。我们用Xnew表示一个新数据,D(Xa,Xb)表示数据Xa,Xb的距离,不妨设为欧式距离,距离越小则相似度越高,训练集为Y={X1,X2,...,XN},于是KNN 算法转化为一个最优化问题:求解Xi,使得D(Xnew,Xi)最小,即min{D(Xnew,Xi)},其中Xi∈Y,Xi 的类型即是Xnew的类型。
显然,上述需求等价于把训练集Y 分割为若干个不相交的子集Yi,即Y = ∪i = 1m Yi,Yi ∩ Yj = ?,i ≠ j。每个线程独立地完成在Y 的所有不相交子集中查找Xnew 的最近邻就等价于一个线程在Y 中查找Xnew 的最近邻。厘清上述问题,技术上实现并行KNN 算法的思路就清晰了。
1.3 并行计算环境的结构
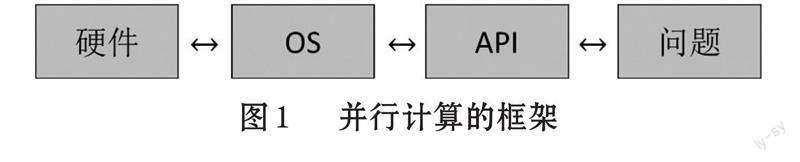
多核CPU 的硬件环境为并行算法提供了基本条件,如何依托于硬件开发并行程序,是一件具有挑战意义的工作。在硬件和问题之间存在一定的鸿沟,厘清这种关系是解决问题的关键,我们可以通过图1 来理解这种关系。
从图1 结构可以分析,多核CPU 解决了硬件并行的问题,操作系统(OS)在硬件与软件开发环境之间搭建了桥梁,实现并行算法的关键只需要利用软件开发环境提供的API 接口实现问题并行求解的设计。Java、Python 等开发环境为并行算法的设计提供了一系列软件包,可以充分利用多线程技术实现并行算法。
2 问题建模及解决方案
本工作以KNN 算法对数据集分类为例进行分析,其总体解决思路是:首先将训练集Y 分割为多个训练子集Yi(i=1,2,…,n),任何两个子集之间不存在重复元素,且所有子集的并为Y;其次使用n 个线程1:1 对应n个训练子集,每个线程只使用分配给自己的训练子集为新数据计算最近邻;最后,每个线程向主程序返回新数据的k 个最近邻,k*n 个最近邻构成最近邻集合P,从P 中选择k 个最近邻为最佳近邻P,以最佳近邻P中类别数最多的为新数据的类别。
2.1 单线程的KNN 算法
基本的KNN 算法描述为:新数据与训练集Y 中的每一个数据进行距离计算,返回与新数据距离最小的数据,该数据称为新数据的最近邻,最近邻的类别即新数据的类别。
这里我们选择最近邻数k 取值为1,若k 值大于1,则上述返回为最近邻集合,以下同样处理。k 取不同的值可以改善分类的准确率,本文不考虑准确率问题,取k 为1 简化程序设计,不影响并行架构,故不进行讨论k 的其他取值。
2.2 多线程KNN 算法
多线程的KNN 算法描述:每一个线程进行新数据与训练子集Yi中的每一个数据进行距离计算,返回与新数据距离最小的数据给主程序,主程序收集的各个线程返回的最近邻构成最近邻集合,以最近邻集合的最佳近邻类别作为新数据的类别。
2.3 数据结构设计
数据结构是算法设计的基础,使用二维数组存储训练集是算法设计的关键。二维数组可以看作是以一维数组为元素的一维数组,不妨用A 表示二维数组,则A0,A1,...,An-1是A 的元素,每一个Ai本身是一个一维数组。Aij 则表示A 的第i 个元素Ai 的第j 个元素。Ai只提供给一个线程使用,作为该线程计算新数据最近邻的训练集。
采用多个线程并行计算新数据在各个训练子集的最近邻中,所有训练集都读入二维数组中,由线程数决定二维数组的行数。若训练集数M 是线程数T的整数倍,则二维数组行数是T,列数是M/T(M 整除以T 的商);若训练集M 数不是线程数T 的整数倍,则二维数组行数是T,前T-1 行列数是M/T,最后一行的列数是M/T+M%T(M 对T 取余数)。
2.4 多线程的创建
KNN 算法需要返回最近邻,带返回值的线程可以通过Java 的接口Callable 定义,并使用接口Future 获得线程的返回值。其定义的一般形式为:
接口Future 的常用方法是使用FutureTask 包装器,它封装了接口Runnable 和Callable,可以便捷的对Callable 对象进行封装并转换为Future 对象。若用于计算一个新数据在训练子集中的最近邻,则TypeData是一个数据对象;若用于计算一组新数据在训练子集中的最近邻,则TypeData 设计为封装了一组数据对象的类。
创建多少线程依据是计算机CPU 核数,一般不超过CPU 的最大核数。程序设计中使用Runtime.getRuntime().availableProcessprs()方法获取CPU 最大核数。
3 实验仿真
3.1 实验环境
实验在一台联想移动工作站上实现,CPU:为Intel(R) Core(TM) I7-8750H,2.2GHz,6 核12 线程,内存为32GB;操作系统及软件开发环境为:Windows11+JDK1.8+IntelliJ IDEA,没有使用其他额外的开发包。
3.2 实验结果
实验中采用具有较大训练集和测试集的数据集进行测试,以此对比并行KNN 算法与串行KNN 算法的效能。数据集使用的是MNIST 手写数据库,它的训练集是60000 张28×28 像素图片,测试集是10000 张28×28 像素图片。本实验使用经过优化处理的MNIST 数据集,图片像素为20×20,并使用3×3 卷积核提取特征,所以训练集与测试集特征维数均为324。
本实验数据集一的训练集为60000,测试集为10000;数据集二的训练集为4000,测试集为10000,其中训练集是通过对每一类的所有训练集进行聚类,每一类的聚类中心400 个,十类就是4000 个聚类中心为训练集。两个数据集的特征维数都是324 维。在不同线程数下构建的KNN 分类器对数据集进行分类的时间如表1 所示。
3.3 分析与讨论
⑴ 从表1 可看出,数据集1 的训练集是数据集2的训练集的12 倍,在不同線程数情况下,对应的耗费时间比稳定在12 倍。
⑵ 对于数据集1 和数据集2 而言,通过图2 可以直观看出,在线程倍增初期具有较好的加速比,中期后加速并不明显。通过在命令行使用wmic 激活环境,使用cpu get *命令查看,CPU 核数为6,过多的线程只能是并发执行,线程切换会增加消耗,加速效果降低,但很明显的是采用不超过核数的多线程构建并行KNN 算法能够显著提高计算速度。
⑶ 实验中取k 值为1,拥有60000 个训练集的分类准确率为97.55%,拥有4000 个训练集的分类准确率为97.22%,所以通过减少训练集数量提高速度的代价是分类效果的减弱。若要既提高速度,又提高精度,就需要进行特征优化,如文献[6,7]所述进行智能算法实现特征选择或者文献[16,17]的特征权重向量学习,评估特征选择结果又需要使用KNN 算法作为适度值函数,此时KNN 算法的计算速度尤为关键。
⑷ 上述数据集2(训练集4000)评价一次特征权重所需时间若优化为8 秒,则使用种群规模为100 的演化计算方法迭代1000次时间T大约是8*100*1000秒,实验时间是约9 天,这个时间基本上可以接受;如果是对数据集1(训练集60000)进行特征选择,同样规模的种群和迭代次数,则需要12*9=108 天,可能这个实验不能接受。通过实验可得出计算数据集特征权重的时间复杂度为O(t*m*n),在m 和n 确定的情况下,只有尽量使用较小的t 才能使智能算法优化特征权重有实际意义。
4 结论
本工作为了提高KNN 算法的计算速度,系统分析了构建并行KNN 算法所需要的条件,并采用Java 编程实现了并行KNN 算法,通过对手写数字数据集的测试,KNN 算法构建的KNN 分类器速度显著提高,为处理大数据提供一种高效的可实践实验方法。该方法简单透明,不需搭建如Hadoop 等复杂计算架构,使得用户只需要解决问题本身,而无需被复杂的计算环境困扰。同时,该工作为智能算法进行特征选择提供了一个案例的实验时间,为数据集特征优化实验提供了对比与数据集规模和特征数所用时间的参照。

