基于深度学习的电力数据分析研究
柳 薇,张 波,梁明源
(国家电网有限公司客户服务中心,天津 300300)
1 引言
随着电力系统[1,2]一体化建设,智能电网中状态估计、故障定位、电压无功控制、需求响应等需求不断增加。然而由于长距离传输,电力供应有限和供电设施建设限制等诸多因素,电力供需失衡已成为一个需要解决的重要问题[3]。为此,可基于通信、计算机、网络[4-6]等技术,通过分析电力客户数据信息,从而有效判断用户用电特征,这对精细化电力管理及电力服务质量提升具有重要意义。
为了提高电力分析的性能,一个重要的问题是基于电力数据确定哪些设备正在运行。这需要从聚合的电力数据中对多个未知数量的电器进行分类。目前,随着深度学习技术的不断发展,分类问题已成果应用于图像、音视频、信号等领域。此外,电力数据作为一种特殊的信号信息,其具备数据纬度高、干扰多、特征复杂等特点,如果直接引入其他领域的深度学习模型,将导致模型性能与分类结果不可靠。为此,许多学者对电力数据分析领域深度学习模型进行研究,并取得了丰硕成果。文献[7]提出了一种基于深度学习的电力系统异常数据自动捕获方法,从而实现对异常传输电子量的精确化处理。文献[8]提出了一种基于深度学习的电力调度数据自动备份系统,从而有效提高电力调度数据稳定性。文献[9]提出了一种基于深度学习的异常用电监测方法。上述模型都在各自领域应用深度学习模型处理电力数据。然而,目前很少有文章基于电力数据对电器进行分类。此外,由于家用电力数据特征复杂,传统方法很难学习到有效特征,导致检测精度较低。
为改善上述问题,引入信号领域特征提取方法,将电力数据转化为频谱图、Mel 频率倒谱系数(Mel-Frequency Cepstral Coefficient,MFCC)和Mel频谱图,从而使得深度学习模型能够充分学习有效特征。此外,提出了一种基于多层堆叠的LSTM 模型,并采用改进的软独热编码提高学习效率及分类准确率。
2 电力数据多层堆叠LSTM 模型
2.1 模型结构
当使用功率数据作为时间序列信息的原始数据时,需要在模拟数据数字化过程中对功率数据进行采样。通过采样过程,数据在每个采样时间可转换为一维数组。然而,一维数据通常非常复杂、不规则或难以发现有效特征。为了解决上述问题,本研究首先对数据进行预处理,从而生成一组有效数据作为深度学习模型的输入。为此,所提网络模型引入音频信号处理方法将电力时间序列数据转换为二维形式的特征提取从而更好地表示数据特征,实现更高效和高性能的学习过程。此外,通过二维形式的特征提取,可以有效减少数据大小,从而在一定程度上加快学习速度。提出的电力数据分析模型结构图如图1 所示。

图1 电力数据分析模型结构图Fig.1 Structure diagram of power data analysis model
通过使用LSTM,可以有选择地不使用来自过去的不必要信息,从而实现更高效的学习。然而,如果数据非常大或整个数据中包含大量重要信息,仅使用一层LSTM 将无法存储数据的所有信息,同时可能会丢失重要信息。因此,提出了一种多层堆叠LSTM 网络来有效地学习时间序列数据的特征。接下来,对网络学习过程中关键步骤进行详细介绍。
2.2 特征提取
将音频信号处理中用于数据表征的技术应用于电力数据的特征提取。电力数据是一种典型的频率和时间共存的长序列数据,为此本研究使用三种特征提取技术:即频谱图、MFCC 和Mel 频谱图,用于提取电力数据的特征,然后将其应用于深度学习模型并提高分类任务的性能。
2.2.1 频谱图
频谱图[11]是一段时间内不同频率下信号幅值的二维表示。频谱图可描述特定时间内每个频率的信号功率以及信号随时间变化情况。基于短时傅立叶变换[12](Short-Time Fourier Transform,STFT)的频谱特征分析进行特征提取。STFT 可以通过将长时间信号划分为等长的较短段并在每个较短段中分别计算傅立叶变换来获得短时傅立叶变换:
式中:w[n]——长度为n的窗口函数;N——窗口数量;x[n]——由n索引的离散时间数据。
最后,可以通过前一个STFT 生成的频谱的线性表示或对数获得频谱图,具体描述为:
2.2.2 MFCC 和Mel 谱图
在Mel 频率尺度上,通过三角形重叠窗口的Mel 滤波器组将频谱转换为Mel 频谱。Mel 滤波器组是一个在正常频率尺度上具有各种带宽的临界频带,通过在低频段而不是高频段放置大量滤波器来强调低频范围内的信息。因此,该方式生成的Mel 频谱图更侧重于降低维数的功率信号的低频模式。
使用离散余弦变换(discrete cosine transform,DCT)[13]将Mel 频谱的对数转换回时间领域,从而获得Mel 频率倒谱系数。通过转换Mel 频谱的对数,扩展了低频信息,并且由于DCT,MFCC 只有实部。具体过程表示为:
式中:sk——滤波器组的第k个滤波器的输出功率;cn——通过DCT 获得的具有N个参数的MFCC。
2.3 多层堆叠LSTM 网络
2.3.1 网络结构
提出了一种多层堆叠LSTM 网络捕获模型,从而有效提高模型的分类和回归能力,改善单层LSTM[9]将无法存储数据的所有信息,同时可能会丢失重要信息的缺点。
多层堆叠LSTM 网络结构如图2 所示,其包含多组前向和后向LSTM 隐含层单元。令电力数据特征向量序列为x=(x1,x2,…,xn),则前向和后向LSTM 从开始到结束同时遍历特征向量,前向神经元隐含层输出序列和后向神经元隐含层输出序列可描述为:
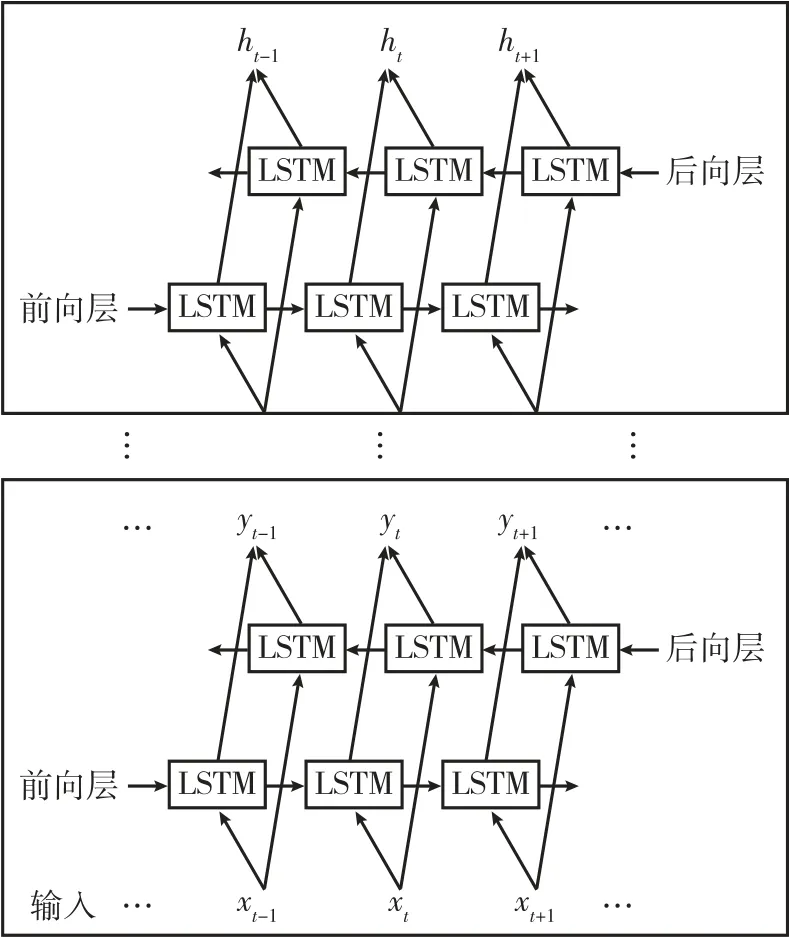
图2 多层LSTM 网络结构图Fig.2 Structure diagram of multi-layer LSTM network
式中:n——特征序列中包含特征的个数。
进一步,双向LSTM 网络隐含层的编码输出yt可以通过级联正向和反向输出求解为:
式中:W,b——与LSTM 相对应的权重向量和偏置。
2.3.2 训练过程
通常情况下,分类任务中最常用的标签编码方法为独热编码[14]。独热编码可以定义为将分类变量转换为分布,从而更好地进行预测。独热编码公式为:
式中:c(k)——第k个类别的标签;K——的数量;Dk——第k个类别的编码。
然而,考虑到电力数据纬度高、特征复杂,模型置信度和过度拟合会导致某些错误序列的特征分数过高,这可能会影响模型训练效果并容易陷入局部最优。为此,本研究提出了一种改进的软独热编码方法,从而防止峰值概率分布,提高模型的泛化能力。
在软独热编码中,不直接使用0 和1 将标签编码为向量,而是使用随机性值对标签编码。对于真实分类,赋予其高概率;但对于其他分类,分配一个服从高斯分布的小随机变量。这将使网络尝试拟合高斯分布并影响适应性,从而增加了标签向量的多样性。因此,软软独热编码计算公式为:
式中:δ——超参数高概率值;μ——分布的平均值或期望值;σ——标准差;x——一个范围内的随机值,用于计算服从高斯分布的随机数;K——类别个数;ε1——服从高斯分布的随机数。
最终,软独热编码下的损失函数计算为:
式中:ce——交叉熵函数;p(t)——网络为输入计算的预测概率分布;q(t)——通过软软独热编码在标签上编码的向量;t——训练集中的时间步长;T——总步长;n——p(t)和q(t)分布的维数。
3 仿真与分析
3.1 数据集
为了验证所提模型的可行性和有效性,本节基于中国某电力公司提供的数据对所提模型进行验证。数据收集时间为2014 年至2017 年,数据集记录了家庭电器级的电力用电情况,采样频率为1/6 Hz,1 Hz和16 kHz。此外,为保证数据有效性,对记录中数据进行清洗,删除部分空缺数据。最终数据集中共记录了329 户共计37 451 组用电数据。需注意,每户都有不同种类和数量的电器的信息,且每户电器的记录时间也存在差异。为充分学习电力数据特征,实验时选取具有代表性的家用电器:台式工作站、洗碗机、笔记本电脑、路由器、冰箱、调制解调器、洗衣机、显示器、微波炉、服务器硬盘、扬声器。同时,电力数据集部分用户及其家用电器用电统计信息如表1 所示。
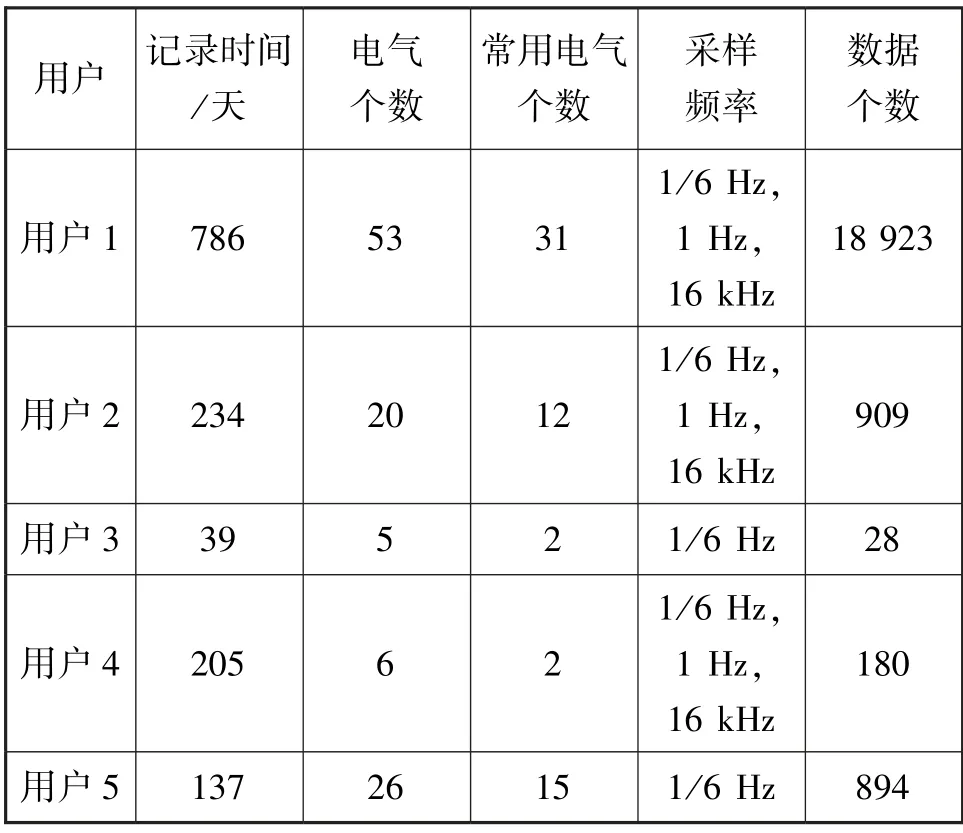
表1 电力数据集部分用户及其家用电器用电统计信息表Tab.1 Statistical information on electricity consumption of some users and their household appliances in the power dataset
3.2 实验过程与环境设置
根据前述特征提取及网络搭建过程,本节对实验步骤进行简要描述。首先,将电力用户数据通过采样步长为M(重叠L)的持续时间进行时序分割。其次,如果分割数据中非零数据小于重叠时间L的1 %,则认为该数据无标签。接着,根据本研究提出的软热编码标记数据集中的每个类。再次,随机排序每个类别时序时间数据集。最后,将数据集按6 ∶4的比例分为训练集和测试集。
此外,为了增加数据量,实验时采用多尺度训练过程,即采样步长分别设置为原步长的[0.5,0.75,1,1.25,1.5]倍。接着,重复上述采样过程,从而完成多尺度采样。多尺度采样不仅可以增加数据量,而且可以更好的表征数据重要前后信息关系。最后,将生成的数据集带入所提多层堆叠LSTM 网络,并基于软独热编码损失函数训练网络参数。
仿真过程中环境设置如下:硬件环境为浪潮服务器,CPU 为Intel(R)Xeon(R)CPU E5 -2680 v3@2.5 Hz(12 核),GPU 为GeForce GTX TITAN X(2块),RAM 为64 GB,操作系统为ubuntu18.04。软件环境为使用python3.7 编译主程序,多层堆叠LSTM 网络基于pytorch 构建。
仿真过程中参数设置如下:学习率为0.001,单个LSTM 隐含层个数为256,优化器为Adam,共堆叠6 层LSTM 单元,数据批处理大小为30,迭代次数为30 000。
3.3 对比与分析
3.3.1 训练性能分析
本节对多层LSTM 模型应用优化策略:软独热编码及多尺度训练。同时对模型训练性能进行评估。
不同策略下训练误差对比结果如图3 所示。可以看出所软独热编码及多尺度训练时,训练曲线收敛速度更快(约80 代达到最优),且更平滑(收敛后误差为0.028)。实验结果验证了所提软独热编码及多尺度训练对加快训练效果具有一定效果。
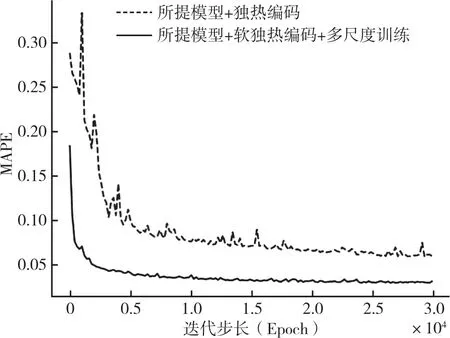
图3 不同策略下训练误差对比结果图Fig.3 Comparison results of training errors under different strategies
3.3.2 交叉对比分析
本节以准确率、召回率和F 分数为指标,对比了所提多层堆叠LSTM 模型与随机森林(Random forest,RF)、支持向量机(Support vector machine,SVM)、循环神经网络(Recurrent neural network,RNN)、LSTM 等模型的性能,从而验证所提模型的优势。不同模型比较结果如表2 所示。可以看出,RNN 和LSTM 等深度学习模型较传统模型(RF 和SVM)相比性能提升明显,然而深度学习模型存在计算复杂,模型执行时间长等问题。同时,所提模型综合性能最高,RF、SVM、RNN、LSTM、等模型召回率较低。分析原因,所提多层堆叠LSTM 网络在对电力数据进行分类时能够充分学习电力特征,从而结合上下文信息进行时空维度学习,提高了分类的精度,最终分类准确率达到89.85 %。此外,电力数据特征复杂,传统模型无法有效搜索解空间,从而容易陷入局部最优,这将严重影响特征分类准确率。
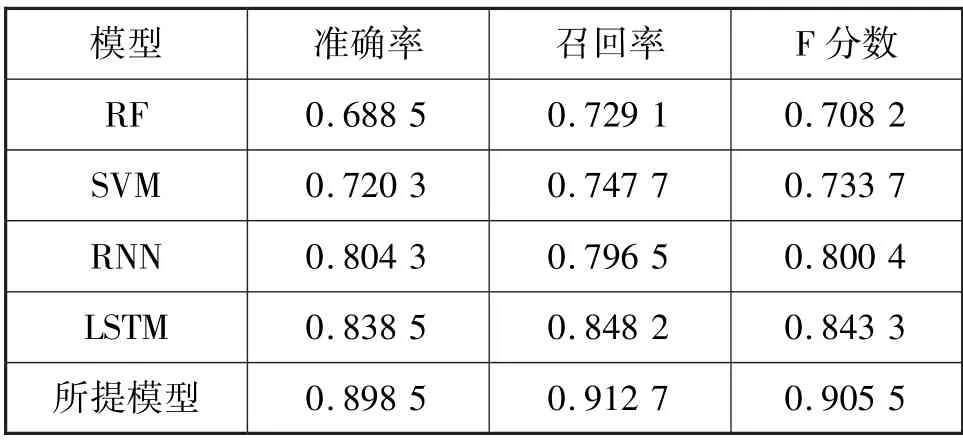
表2 不同模型比较结果表Tab.2 Comparison results of different models
4 结束语
建立了一种基于深度学习的电力数据分析模型。该模型参考音频信号处理中多特征提取方法,并结合LSTM 模型实现了家庭级别电力信息的有效分类。该模型为电力系统智能化管理及特征分析提供了一定借鉴作用。未来可对最优化模型参数的优化配置和规模进行研究,从而进一步降低模型计算消耗。
另外,感谢国网客服中心2022 年“网上国网”App埋点综合分析服务项目(编号:SGKFYYOOZCJS2100039)的资助和支持!

