基于单片机的高精度波形信号直接生成方法研究

陈砚圃,刘 含,郭 博,石立春

(1.西京学院计算机学院,西安 710123;2.西京学院电子信息学院,西安 710123)

1 引言

利用波形信号生成技术生成各种特定波形信号,在航空航天、通信、导航、雷达、测控、医疗等领域的应用极其广泛[1-5]。直接数字频率合成(DDS)技术[6]能够对信号的频率、相位、幅度等参数进行精确控制,是普遍采用的波形信号生成技术。而直接利用DDS 专用芯片或借助FPGA 通用器件,是实现DDS 技术最常见的两种解决方案[7,8]。另一方面,随着单片机(含嵌入式微控制器)的主频、CPU位数、存储器容量的提高以及其片内集成的外设越来越丰富,电子装置的诸多功能由单片机直接实现已成为趋势。为了节省电路、降低成本并提高系统的可靠性,特别需要对基于单片机直接生成波形信号的方法进行研究。

为了能够直接生成信号,须选用主频高且片内嵌有数模转换器(DAC)和直接存储器存取控制器(DMA)等外设的单片机。利用DMA 并结合DAC,完全不占用单片机CPU 的时间即可将离散序列自动转换为模拟信号。由于DDS 在实现过程中需要连续进行相位累加求和及相位的高位截取等操作,而DMA 仅支持数据的自动传送功能,故DDS 技术并不适于单片机直接实现。单周期循环法[9]虽然能够在DMA 模式下直接实现,但其生成信号的频偏过大。综合考虑单周期循环法与DDS 技术的优点,提出了一种整周期循环波形信号生成方法。该方法通过对多个周期(整周期)的信号波形进行等分离散以增加预存信号离散值的个数,因而可有效提高生成信号的频率精度,且能够在单片机的DMA模式下直接实现。

2 单周期循环波形信号生成法

单片机直接生成波形信号最简单的办法是将1个周期内的波形离散值逐次经DAC 后循环输出,并通过控制相邻离散值之间的读取时间完成对信号频率的控制。对正弦信号,1 周期内的Nwav个等间隔离散值为:

式中:bDAC——单片机片上DAC 分辨率;round[·]——4 舍5 入取整函数。

由于DAC 的输出为单极性电压,方括弧中的第二项(直流分量)可避免Nwav个离散值Vwav[n]取负值。

3)计算周期数NT和定时系数Ar

式中:fclk——定时时钟频率(fclk=1/tclk)。

受DAC 转换时间的限制,定时系数Ar存在最小值Amin,生成信号的最高频率为:

在单片机系统中,定时时钟周期tclk为固定的常数,且生成信号的周期只能取其整数倍,这将导致生成信号的频率fo与预设频率fs之间存在误差。设Nwav取常整数,Ar可变但只能取整数,显然Ar的误差在±0.5 之内,因而生成信号的最大相对频偏为:

梨花松开方竹沿河而行，她知道从此一别，就是永生。梨花走在河北岸，方竹走在河南岸；俩人依旧默默地隔河而行，边走边你看我一眼、我看你一眼。不知不觉，又回到他们相遇的地方，彼此都站住了。良久，梨花让方竹先走；但方竹不走，他让梨花先走。方竹说：“回去吧！回去……”梨花依旧没动。方竹又挥手道：“回去吧！回去……”梨花这才毅然转过身去，眼泪就哗地涌了出来。她小跑了几步，突然又站住了，转过身来，只见方竹依旧站在河边，呆呆地望着她，她就转身跑了。

式中，Ci为重金属i在土壤中的实测含量(mg/kg)；Bi为重金属i在土壤中的背景值(mg/kg)。通常对于重金属i：Igeo≤0，土壤无污染；0 5，土壤极强污染。

2.1 专家基本情况 11名受咨询专家中，平均年龄45.0 岁;职称:高级占 81.8%，中级占 18.2%;学历:本科占 27.3%，硕士占54.5%，博士占 18.2%;另外，博导及硕导占72.7%。

由此可见,单周期循环法生成信号的最大频偏与信号的频率成正比。例如,当fclk=100 MHz,Nwav=100 时,生成信号的频率fo在100 kHz 附近的最大频偏可高达5 kHz。为了降低信号频偏,一方面尽可能选择主频高的单片机,另一方面应减小信号在1 周期内离散值的个数Nwav。但Nwav越大信号波形的质量也就越高,为了得到高质量的信号波形,一般要求Nwav不低于32。

3 整周期循环波形信号生成法

接连进攻了三天，鬼子在一八八团五连阵地前丢下了二三百具尸体，这些尸体有的只是一块块烂肉，挂在铁丝网上，鹿砦上，太阳一晒，尸块都成了酱黑色。也有整尸的，穿戴齐整的，是两天前被打死的。死了两天的鬼子没人收尸，晚上一阵雨，白天太阳晒，死人很快涨得和发面一样。

受单周期循环法和DDS 法的启发,为了在单片机的DMA 模式下直接生成具有精确频率的波形信号,提出整周期循环波形信号生成法。与单周期循环法不同的是,整周期循环法用到的Nwav个信号离散值Vwav[n]是在多个周期(整周期)内对波形信号等分离散的结果,这样在相邻离散值的间隔不小于DAC 转换时间的前提下仍可增大Nwav,进而提高生成信号的频率精度。

对正弦信号的NT个信号周期等分Nwav等份后的离散值为:

水仙芝的心是稚嫩的，没往深处想。在她看来，蒋海峰是班长，找她是正常的。而蒋海峰跟她谈话，也是从班上的事情谈起。面对蒋海峰侃侃而谈，水仙芝保持沉默，偶尔微微一笑。

受DAC 转换时间的限制,定时系数Ar存在最小值Amin,信号的最高频率为:

为了使生成信号的频率尽可能精确,先根据预设参数求出Ar,Ar取整后再修正Nwav。由于Ar和Nwav为整数,二者在取整过程中带来的最大误差均为1/2,因而生成信号的最大相对频偏近似为:

需求参数:信号频率fs,最大相对频偏em;

廖：阴阳互根、福祸相倚，中国传统文化中的道家哲学思想，在我身上得到了充分的体现.没有现代自然科学的系统学习，使得我能够较为容易地理解中国传统医学的理论；不如意的现实生活状况，逼迫一个只有小学文化水平的人，在公布“恢复高考”后的一个月时间中，拿下了“跳龙门”所必须掌握的知识；正规的医学院校教育，使得两种截然不同的医学知识体系在我头脑中冲突、碰撞，归于理解；毕业后没有去作医生，而是改治自己原本最不喜欢的历史，又为理解传统医学增添了新的视角.

整周期循环情况下只要在足够多的周期内对信号进行离散,就能得到足够大的Nwav,进而可使生成信号的频率精度足够高。

预设信号的Nwav个离散值Vwav[n]预存于存储器中,单片机的DMA 在定时器的定时触发下,完全不占用CPU 时间,每间隔Ar个定时时钟周期tclk依次循环读取Vwav[n]并送至DAC 输出,生成信号的频率为:

基于单片机的DMA 模式和整周期循环算法生成波形信号时,首先依据预设的最大相对频偏由式(9)初步估计信号离散值的个数Nwav。例如,当要求相对频偏在±0.5 %之内时,取Nwav=100。其次,依据所选的单片机确定定时器的时钟周期tclk、最小DAC 时间间隔tmin以及DAC 分辨率bDAC等参数。单片机以自动循环DMA 方式逐次读取预存的波形数据并送至DAC,触发相邻两次DMA 操作的时间间隔不得小于tmin。进一步,依据Nwav,tclk,tmin以及预设频率fs计算波形离散所需的周期数NT和定时触发DMA 操作对应的定时系数Ar,并由取整后的Ar更新Nwav。最后由式(5)计算Nwav个波形信号离散值Vwav[n]并预存于存储器中。完成以上设置与计算工作后,启动单片机的定时器、DAC 以及DMA 等片上外设,单片机将在DMA 方模式下自动生成指定频率的正弦波信号。

波形信号生成的单周期循环法是将信号在1个周期内等分后的离散值循环送至DAC 而实现的,且受DAC 转换时间的限制离散值的个数Nwav也存在下限,这正是信号频偏过大的主要原因。其实只要能动态获取各离散时间信号的精确相位,再在存储器中读取相位最接近的信号离散值并送至DAC即可实现对信号频率的精确控制。这正是DDS 波形信号生成方法的核心,该方法突破了在1 个周期内对信号等分离散的要求,生成信号的频偏非常小。但是DDS 在实现过程中需要连续进行相位累加求和及相位的高位截取等操作,通常要借助DDS专用芯片或FPGA 器件才能实现,在单片机的DMA模式下无法完成。当单片机工作于定时中断模式时能够完成DDS 的全过程,但频繁的中断响应、相位累加、相位截取、波形离散值读取、DAC 装载、中断返回等操作不仅耗费了大量CPU 时间,同时也极大地限制了生成信号的频率范围。

基于单片机和整周期循环法生成正弦信号的具体流程如下:

下变频电路设计中只使用两个射频锁相环，设置RF1锁相环与RF2锁相环的VCO中心频率分别为1 580 MHz与1 220 MHz，则锁相环可输出频率范围分别为1 501～1 659 MHz，1 159～1 281 MHz。两个锁相环的输出采用复用输出管脚，所以最终本振频率的输出范围就是这两个频率范围的组合。

1)预设参数

今年48岁的王建云，有着30多年的果树种植管理经验，在果树的选育、栽培、水肥管理等方面可谓样样精通。他的12亩果园虽然也遭受了严重的冻害，但同与其毗邻的果园相比，他的果树在采摘结束后仍未脱肥，叶片浓绿，树势健康。随手一抓，能明显感受到土壤松软深厚。

可以看出最大相对频偏随频率的提高而增大。而且在信号的高频端上式取最小值中的第1 项大于第2 项,故在整个生成信号的频率范围内,最大相对频偏近似为:

单片机参数:定时器时钟周期tclk,最小DAC 时间间隔tmin,DAC 分辨率bDAC;

2)估计波形离散值个数

Nwav=round(1/(2em));

除了人为上的管理，交通安全管理设备也是保证学校内部交通安全的基础，高校需要更新校园内的限速标示，使进入学校内的人员可以明确校内的行车要求，还需要改善测速设备，保证数据接入视频识别系统，并且还需要针对限速要求较高的地区，专门配置减速带，限制校园内的车速。

将波形信号在1 个周期内的Nwav个离散值Vwav[n]预存于存储器中,在单片机定时器的控制下每隔Ar个定时时钟周期tclk依次读取预存的Vwav[n]并送至DAC,进而生成波形信号。信号的频率为:

NT=ceil(Nwavtminfs);(ceil(·)为向上取整函数)

Ar=round(NT/(Nwavfstclk));

4)更新Nwav

Nwav=round(NT/(Ar fstclk));

5)由式(5)预设波形离散值

内容资源建设是各互联网期刊主要出版商的重要工作，资源建设的广度和内容挖掘的深度决定了各平台的服务能力与发展潜力。因此，各平台都非常重视该项工作，具体情况见表7。

6)启动单片机的定时器、DAC 以及DMA

4 波形信号单片机直接生成实验

根据波形信号单片机直接生成的理论,为了使输出信号的频率范围尽可能宽、频率尽可能准以及波形质量尽可能高,应选择片内嵌有大容量数据存储器(SRAM)、高速DMA、高速定时器以及高速DAC 的单片机。以下实验中采用型号为STM32F407ZGT 的中高端单片机。该单片机在国内使用普遍,相关特色有:系统时钟频率fsys=168 MHz,SRAM 的容量为192 KB,支持1 次最多传送65536 个数据的DMA,12 位的高速DAC。该单片机片上定时器分为高级定时器、通用定时器和基本定时器,实验中采用输入时钟频率fclk=84 MHz 的基本定时器触发DMA,进而自动完成预存波形值的读取并送至DAC 生成模拟信号。另外实验发现,在最小定时间隔tmin不低于8tclk时该型号单片机的DAC 能够正常工作。

首先对单周期循环法生成正弦信号进行实验。为了便于与整周期循环法进行比较,实验中预存的信号离散值个数固定,Nwav=100。由于受tmin=8tclk的限制,生成信号的最高频率大约为100 kHz。实验中分别在100 Hz,1 kHz,10 kHz 及100 kHz 等频点附近对所生成的正弦信号进行了测试,实验表明生成信号的幅度稳定、波形质量好。Nwav=100 时单周期循环法生成不同频率的正弦波信号时对应的最大频偏如表1 所示,其中的预设频率值由实际频偏较大时对应的频率给出,最大频偏是由式(4)给出的理论值。可以看出,生成信号最大频偏的实际值与理论值非常吻合。但信号频偏随频率的升高而显著增大,在100 kHz 附近最大频偏可达6 kHz。

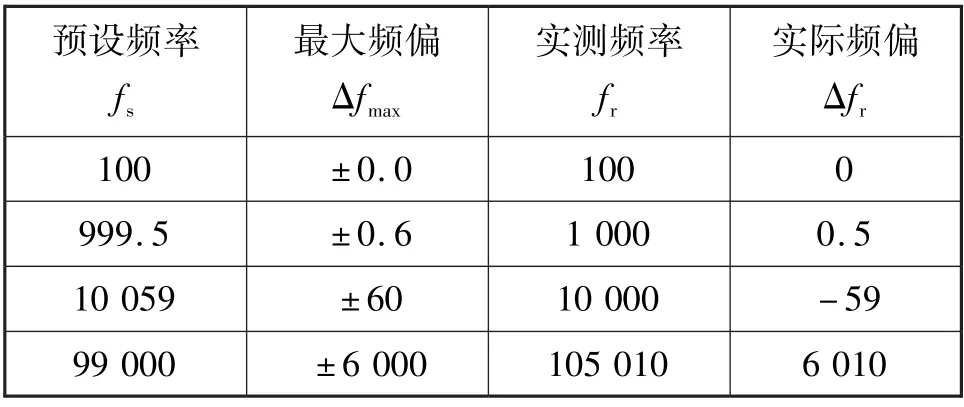
表1 预设Nwav=100 时单周期循环法的最大频偏Tab.1 Maximum frequency deviation of single-period repetition method when Nwav=100 is preset 单位:Hz

考虑到整周期循环法生成的波形信号的频偏主要由波形离散值的个数Nwav决定,因而除了改变生成信号的频率外,还通过改变波形离散值的个数Nwav进行测试。当预设Nwav=100,1 000,10 000 时整周期循环法所生成信号的频偏如表2 至表4 所示,其中的最大频偏由式(9)给出,可以看出最大频偏的实测结果与理论估计非常吻合。由表1 与表2可知在高频端(100 kHz 处),相对于单周期循环法,整周期循环法的频率精度提高了1 个数量级。比较表2 至表4 的结果可知,生成信号的最大频率偏差与信号的离散个数Nwav成反比,Nwav越大频率的精度就越高。对整周期循环法,波形的离散值取自多个周期,通过增大周期个数增大Nwav,进而提高频率精度。但受单片机片内存储器容量的限制,Nwav的取值是有上限的。对STM32F407ZGT 单片机,Nwav可以取至10 000,对应的生成信号最大相对频偏为仅有0.5×10-4。

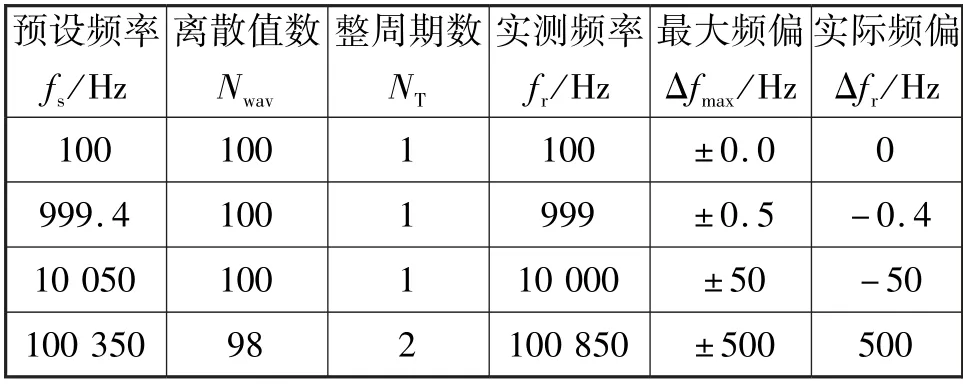
表2 预设Nwav=100 时整周期循环法的最大频偏Tab.2 Maximum frequency deviation of integer-period repetition method when Nwav=100 is preset

表3 预设Nwav=1 000 时整周期循环法的最大频偏Tab.3 Maximum frequency deviation of integer-period repetition method when Nwav=1 000 is preset

表4 预设Nwav=10 000 时整周期循环法的最大频偏Tab.4 Maximum frequency deviation of integer-period repetition method when Nwav=10 000 is preset

为了得到高质量的信号波形,一般要求在1 个信号周期内不低于32 个离散值,又由于实验中的最小定时间隔tmin不小于8tclk,理论上生成信号的频率可高至330 kHz。但是,以上实验只给出了频率在100 kHz 之内的生成信号的结果,这是因为当频率高于100 kHz 时STM32F407ZGT 单片机生成信号的幅度和波形质量会逐渐下降。当Nwav=10 000,预设频率fs分别为10 kHz,100 kHz,150 kHz,200 kHz时,用示波器对生成信号的实测结果如图1所示,频率测量值分别为10.000 kHz,100.01 kHz,150.01 kHz,200.01 kHz。频率为10 kHz 和100 kHz时信号的幅度一致(峰峰值均为2.88 V)且波形无失真,频率为150 kHz 时峰峰值已降至2.66 V,频率为200 kHz 时峰峰值为2.48 V 且波形畸变为三角波。信号波形的这种失真主要是由单片机片内的DAC 缓冲输出放大器的压摆率较低造成的。为了提高不失真信号的频率,需选择片内具有压摆率更高的DAC 缓冲输出放大器的单片机。

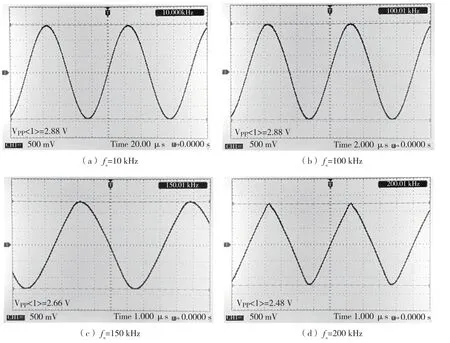
图1 整周期循环法生成正弦信号的显示波形图Fig.1 Sinusoidal signal waveform generated by integer-period repetition method

5 结束语

通过在整数个周期内对信号进行等分离散获取波形信号的预设离散值,提出了生成波形信号的整周期循环法。该方法借助片内嵌有DMA 和DAC 等外设的单片机,无需引入外围芯片即可直接生成预设的波形信号,且在生成信号时完全不占用单片机的CPU 时间。导出了整周期循环法生成波形信号的频率及最大相对频偏公式,给出了算法实现流程。理论分析表明,只要利用足够多的信号周期获得足够多的预设波形离散值,即可满足预设的频率精度。采用STM32F407ZGT 型单片机对整周期循环法生成的正弦信号进行了实验测试。实验表明信号波形稳定、质量好,实测结果与理论相吻合,信号的最大频偏与预设波形离散值的个数成反比。