多因素作用下浑水入渗对土壤导水特性的影响

康守旋 ，费良军 ※，钟 韵 ，赵彭辉 ，杨 震 ，樊倩雯

（1. 西安理工大学省部共建西北旱区生态水利国家重点实验室,西安 710048；2. 三峡大学三峡库区生态环境教育部工程研究中心,宜昌 443002）

0 引言

中国黄河流域大部分区域降水稀少[1-2]，农业灌溉用水严重不足[3-4]，制约了当地农业发展。该区域降雨分布集中，水土流失严重[5]，使得黄河成为世界上含沙率最高的河流[6]。为充分利用水资源来满足农业灌溉用水的需求，该地区的一些灌区大力开展引浑灌溉。浑水灌溉可以在提高水资源利用率的同时改良土壤、增加土壤肥力。进入农田的浑水入渗时，部分泥沙颗粒随水分运移进入土壤中，滞留在土层内，形成滞留层，而浑水中大部分泥沙颗粒逐渐沉积在土壤表面，形成沉积层。滞留层和沉积层共同形成了结构不同于原土的致密层[7-9]，从而改变了上边界入渗条件，对入渗过程产生影响。因此，深入研究浑水入渗过程对缓解引浑灌区水资源紧缺、扩灌增产和提高灌溉质量等具有重要的理论价值和现实意义。

浑水灌溉是引用含沙河水作为水源进行灌溉。浑水在进入田间后，其所含的泥沙随水流推进、沉降，在土体表面产生致密层，形成了不同于清水的土壤水分入渗规律[10-11]。一些研究采用浑水试验方法探索浑水入渗规律及影响因素[12-13]，发现：累积入渗量与入渗时间呈幂函数变化关系[12]；浑水含沙率、泥沙颗粒级配、土壤容重及土壤初始含水率等均能影响浑水入渗[14-16]；入渗率和湿润锋运移距离随浑水含沙率的增大而减小[16]；泥沙中小于0.01 mm 颗粒含量越大，阻渗作用越显著[17]；浑水入渗能力和湿润锋运移距离均随土壤容重的增大而减小[18]。也有研究分析了膜孔灌溉下的浑水入渗规律[19-21]：LIU 等[22-23]研究了不同浑水肥液浓度和初始含水率下浑水膜孔灌的累积入渗量变化规律、水分分布和再分布及氮素分布规律；姜瑞瑞等[24]研究了不同膜孔直径下多向交汇浑水入渗湿润体特征及灌水均匀度。另外的研究关注了浑水入渗模型，如引入遗传算法拟合带有经验值的Kostiakov 模型[17]、将浑水入渗形成致密层的阻渗作用归结为湿润锋平均吸力值的Green-Ampt 模型[25]、利用浑水波涌灌大田试验数据并结合Kostiakov 模型推导了3 种经验模型[26]。除农业领域外，浑水入渗在环境、工程方面也得到广泛关注[27-31]。

浑水入渗过程中，所形成致密层阻碍了水分入渗，减小了入渗量。随着浑水入渗量的减小，浑水中形成致密层的泥沙量也将变少，使得致密层厚度增加速率变缓，土壤入渗能力不至于急速减小。因此，浑水入渗过程是入渗量变化与致密层阻渗能力相互影响的过程[18-19]。除入渗量外，致密层导水能力与其内部孔隙大小、结构有关[32-33]，即形成致密层的浑水泥沙数量及粒径（含沙率及泥沙颗粒级配）对致密层导水能力造成影响。通常采用土柱来确定土壤的导水能力[34]，为了便于研究入渗过程，减少不可控因素，已有研究采用饱和土柱进行浑水渗流试验，来探索该状况下导水能力的变化规律[8]。利用数值模拟方法来探索土壤入渗特性已成为研究热点，如介飞龙等[35]采用椭圆方程来模拟膜孔灌湿润锋形状，研究了初始含水率对膜孔灌湿润体特征的影响；冯正江等[36]在使用小波分析和通径分析法分析Kostiakov 模型标定因子和土壤特性参数的基础上，利用多元线性回归、BP 神经网络和支持向量机建立估算标定因子的土壤传递函数；王晓彤等[37]利用Hydrus-1D 软件来模拟分析黄河泥沙充填复垦土壤的入渗和蒸发特性，优化了复垦土壤的夹层结构，为研究设计黄河泥沙夹层式土壤剖面提供了一种可靠方法。

目前，现有研究多集中在浑水入渗特性、影响因素及入渗模型等方面，缺乏浑水入渗致密层形成过程对导水能力影响的研究。在致密层形成过程中，水分入渗上边界条件不断变化，土壤的导水能力也随之改变。研究致密层在土体表面形成后，不同因素下导水能力变化规律对揭示浑水入渗机理具有十分重要的意义。因此，为了探究浑水入渗对土壤导水能力的影响，本文进行饱和土柱浑水渗流试验，深入分析多因素（含沙率、泥沙颗粒级配、入渗时间）对致密层形成条件下土体导水能力的影响，建立多因素导水率动态模型，为进一步揭示浑水入渗规律提供理论依据。

1 材料与方法

1.1 供试材料

供试土样采自引黄灌区0～30 cm 深度范围的农田土壤，采样地点分别为西安市灞桥区、西安北郊及宁夏吴忠市。土壤样品自然粉干碾碎后，过2 mm 筛以备使用。土壤粒径采用Mastersizers-2000 型激光粒度分析仪(英国马尔文仪器公司，测量范围为0.02～2 000 μm)测定，结果如表1 所示。按照国际制土壤质地分类标准，采自西安灞桥、西安北郊、宁夏吴忠的土样分别为粉壤土、砂壤土及砂土。

表1 试验土壤和泥沙粒径组成Table 1 Particle size composition of tested soils and sediments

入渗试验浑水中所含泥沙取自泾惠渠灌区干渠，取回的泥沙经风干过1 mm 筛，人工配置出不同颗粒组成的5 种泥沙，其中3 种不同级配用于多因素试验，按照黏粒含量大小分别记为J1（低黏粒含量）、J2（中黏粒含量）及J3（高黏粒含量），剩余2 种（Y1 和Y2）用于验证试验。

1.2 试验设计

开展多因素试验研究浑水含沙率（3%、6%、9%）和浑水泥沙种类（J1、J2、J3）对砂土饱和土柱入渗的影响并建立入渗模型。各组试验各进行3 次重复。为了验证多因素浑水入渗模型的可行性，另外设置了8 组试验。共计17 组试验，具体方案如表2 所示。

表2 浑水入渗试验方案Table 2 Experimental scheme of muddy water infiltration

1.3 试验过程

浑水配置：按照试验设计选取泥沙种类，并依据含沙率称量相应质量的泥沙和去离子水，将其倒入马氏瓶后充分搅拌以配置浑水。

试验装置准备：2022 年5 月在西安理工大学农水试验大厅进行试验。浑水饱和土柱入渗装置由土柱和浑水马氏瓶两部分组成，如图1 所示。土柱材质为有机玻璃，内径为5 cm、高为13 cm，为了通气和更好收集土柱渗出的水流，底部装有开孔的垫片，并在土柱底盖加有管嘴。试验前，按预定容重分层填装土壤，层间刮毛，装土高度为8 cm。为防止土壤从底部小孔中损失，装土前在底部垫入滤纸。将装好的土柱在水中浸泡12 h，使其饱和后进行饱和土柱浑水入渗试验。

图1 试验装置图Fig.1 Schematic diagram of experimental apparatus

试验过程：为保持稳定的浑水含沙率，将马氏瓶与磁力搅拌器结合组成浑水马氏瓶进行入渗。将带有磁性的搅拌子放入装有浑水的马氏瓶中，再将马氏瓶放置于磁力搅拌器上，利用磁场力使浑水马氏瓶内的搅拌子进行旋转来不断搅拌浑水，保持浑水含沙率的稳定。浑水入渗前，为排除初始渗流速度的影响，先进行清水入渗，待入渗稳定后，再进行浑水渗流。在管嘴下放置量筒，按照先密后疏的时间间隔量取渗出水的体积并记录，以计算出不同时间的导水率。根据Darcy 定律[38]，流量与水力梯度成正比，即：

式中q为渗透流量，cm3/min；Kh为导水率，cm/min；i为水力梯度；A为土样的横截面积，cm2。

当浑水入渗时，饱和土柱上界面会发生变化：部分泥沙颗粒随水分运移进入土壤中，滞留在土层内，而浑水中大部分泥沙颗粒逐渐沉积在土壤表面改变了土壤导水性能，使得导水率不断发生变化而无法准确获得，这里使用一段时间间隔的平均出流量来代替渗透流量，再利用式（1）计算得出不同入渗时刻的土柱导水率值。平均出流量与导水率存在以下关系为[8]

式中Q(t+Δt)为一段时间间隔后出流量，cm3；Q(t)为时间间隔前出流量；Δt为时间间隔，min；二者比值为一段时间间隔平均出流量，近似为渗透流量。

1.4 评价指标

为评价模型准确性，利用统计学中决定系数（R2），均方根误差（SRMSE）和相对误差绝对值均值（SMARE）对模型中计算值与试验实测值之间的符合度进行评价分析。通常R2越接近于1，SRMSE和SMARE越接近0，表明模型计算精度越高，即实测值与计算值越接近。

2 结果与分析

2.1 多因素影响下导水率动态变化

根据不同处理浑水饱和土柱入渗试验，得到每组试验的导水率值随入渗时间的变化过程（图2）。由图2可以看出，导水率随入渗的进行不断减小，在同一入渗时刻，各组试验累积入渗量存在差异，表明各因素对导水率影响程度不同。

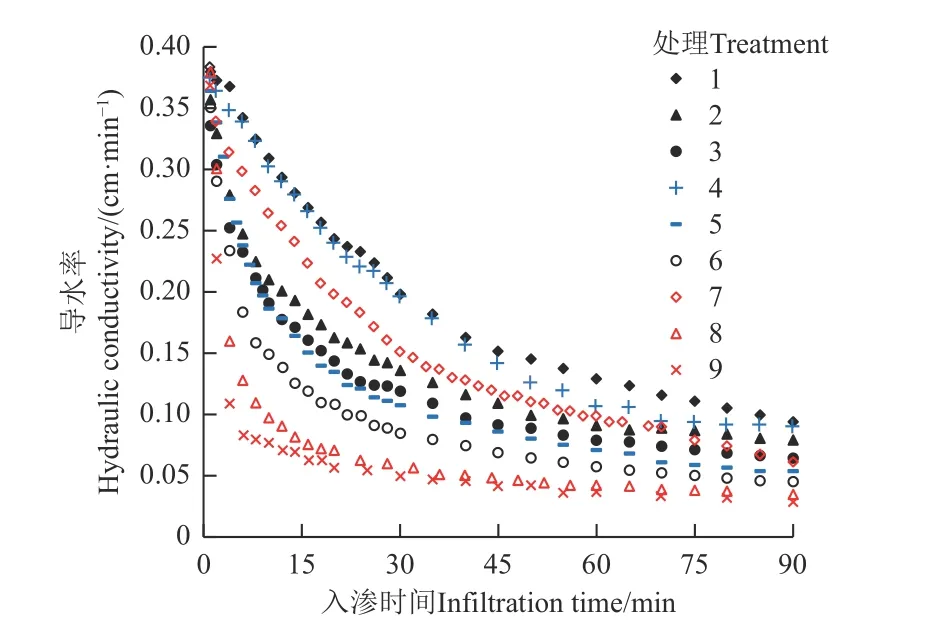
图2 不同试验处理导水率随时间变化Fig.2 Hydraulic conductivity versus time for different treatments

为进一步分析各因素对饱和土柱入渗下导水率的影响，采用多因素方差分析方法分析浑水含沙率与黏粒含量（体积分数）对导水率的影响，结果见表3。由表3可知，浑水含沙率、各颗粒含量和入渗时间对导水率影响极显著(P＜0.01)。

表3 不同因素不同水平对导水率的影响Table 3 Effects of different factors and different levels of hydraulic conductivity

采用多元回归法[39-40]构造浑水含沙率和＜0.002 mm颗粒（黏粒）含量影响下导水率的动态经验计算式：

式中S为浑水含沙率，%；N为黏粒含量%；a为导水能力系数；b、c、d分别为各项因素的指数。

多元回归分析结果如式（4）所示，R2为0.853，SRMSE为0.004 cm/min，模型拟合效果良好。

所求经验模型（式（4））中包含3 个影响因素，不同因素之间单位和数量级存在差异，为分析各因素对导水率影响的重要程度，对数据进行标准化处理，处理后b、c、d的标准系数分别为-0.422、-0.295 和-0.789，表明浑水含沙率、黏粒含量和入渗时间对单位膜孔面积累积入渗量均有影响，其中受入渗时间影响最大，浑水含沙率次之，黏粒含量影响最小；标准系数均小于0，表明导水率随入渗时间、浑水含沙率和黏粒含量间增大而减小。

为检验式（4）的可靠性，利用试验处理10、11 对其进行验证，将试验实测值和模型计算值进行对比分析，结果见图3。图3 中模型（式（4））和实测值间SMARE分别为6.99%和5.93%（小于7%），SRMSE分别为0.008和0.006 cm/min（处理10 和11），总体误差较小（小于0.01 cm/min），说明所建的动态模型能有效地描述导水率与各因素及入渗时间的量化关系。

图3 砂土导水率实测值和计算值Fig.3 Measured and calculated values of sand soil hydraulic conductivity

2.2 多因素影响下导水率变化率动态变化

将导水率对入渗时间求导数，即得浑水饱和土柱入渗条件下土壤导水率随入渗时间变化的函数关系：

式中k为导水率变化率，cm/min2。从式（5）可以看出，导水率变化率随入渗时间的延长逐渐减小，当时间足够长时，导水率变化率逐渐趋于0，导水率趋于稳定。

由于不同因素对导水率变化率的影响不同，分别取其对含沙率、黏粒含量求偏导数的绝对值，分析导水率变化率受各因素影响的敏感程度[39]。

通过式（6）和式（7）可分别定量计算出浑水含沙率、黏粒含量对导水率变化率的敏感性指标，敏感性指标越大，相应因素变化对导水率变化率的影响越大。各试验处理下导水率变化率均随着各因素增大而减小，故以处理1 为例，计算出各因素对导水率变化率的敏感性指标，点绘其随各因素变化的曲线，如图4 所示。

图4 处理1 导水率变化率敏感性指标与各因素关系Fig.4 Relationship between sensitivity of hydraulic conductivity change rate and each factor in experimental treatment 1

由图4 可知，各敏感性指标随着相应因素增大而明显减小，表明含沙率和黏粒含量变化对导水率变化率均有显著影响；含沙率敏感性指标为1.64×10-5～2.60×10-3，黏粒含量敏感性指标为4.95×10-5～2.10×10-3，表明黏粒含量和含沙率对导水率变化率影响程度十分接近。入渗时间对各敏感性指标的影响较大，在入渗时间为10 min时，随着各因素的增大各敏感性指标减小幅度较大，而在入渗时间为30 和90 min 时，各敏感性指标变化幅度明显减小，在10 min 含沙率敏感性指标随着含沙率的增大而减小了2.2×10-3，而入渗时间为30 和90 min 仅分别减小了5×10-4和1×10-4。这也说明随着入渗的进行，导水率变化率对含沙率和黏粒含量的敏感程度逐渐降低，各因素影响下导水率变化趋势相一致。

2.3 不同土壤质地下动态导水率模型的适用性

土壤质地对土壤孔隙大小、形态及分布产生很大的影响，因此不同质地的土壤其饱和导水率一般不相同。

式（3）中包含了导水能力系数项（a）、含沙率影响项（Sb）、泥沙颗粒级配影响项（Nc）及时间影响项（td）。浑水饱和土柱入渗条件下，部分泥沙进入土体中，而泥沙沉积在土柱表面形成沉积层时会受到入渗速率的影响。为了便于研究，若忽略此影响并不考虑滞留层的作用，则沉积层内部结构是连续均匀的。当含沙率和泥沙相同时，形成的沉积层结构相同，其厚度随时间不断变化，因此导水能力只受到入渗时间和土柱中土壤土质的影响。

对于不同土质的浑水饱和土柱导水率动态模型，由砂土得出的含沙率影响项（Sb）和泥沙颗粒级配影响项（Nc）中的指数仍然有效，只有导水能力系数项（a）和时间影响项（td）不同。即不同土质浑水饱和土柱入渗下，导水率模型为

分别选取处理12 和15（土质分别为砂壤土和粉壤土，含沙率S均为6%，黏粒体积分数N分别为4.22%和1.01%）来推求式（8）中的导水能力系数a、时间指数d。此时式（8）中S、N值均已确定，式（8）可视为导水率随入渗时间变化的幂函数：

式中α为拟合系数，α与导水能力系数a、含沙率影响项Sb、泥沙颗粒级配影响项Nc存在以下的关系：

图5 为处理12 和15 导水率随入渗时间变化图，对导水率和入渗时间进行幂函数拟合（见图5），拟合结果如下：

图5 处理12 和15 导水率随入渗时间变化Fig.5 Hydraulic conductivity versus time for treatments 12 and 15

图5 中拟合结果的决定系数分别为0.912 和0.930（处理12 和15），SRMSE分别为2×10-3和5×10-5cm/min（处理12 和15），说明式（8）对处理12 和15 拟合结果良好。由此得出砂壤土和粉壤土的时间项指数d分别为-0.081 和-0.062，分别将处理12 和15 中的S和N值代入式（10）后得到砂壤土和粉壤土的导水能力系数a分别为0.059 和0.011。

得出由处理12 和15 推求的a、d值后，将其代入式（8），即可得到砂壤土和粉壤土导水率动态模型，分别如下：

为检验式（13）和式（14）的可靠性，分别利用试验处理13、14、16 及17（处理13、14 土质为砂壤土，处理16、17 土质为粉壤土）对其进行验证，将试验实测值和模型计算值进行对比分析，结果见图6。图6 中试验实测值和动态模型（式（13）和式（14））计算值的SRMSE分别为2.1×10-3、1.2×10-3、6.0×10-4及3.0×10-4cm/min（＜0.01 cm/min），SMASE分 别 为16.58%、14.90%、15.50%及10.46%（处理13、14、16 及17），均小于17%，所建立的砂壤土和粉壤土动态模型仍能有效地描述导水率与各因素及入渗时间的量化关系。土壤质地为粉壤土（处理16、17）的导水率动态模型SRMSE、SMASE均小于砂壤土（处理13、14），模型模拟效果更好，这是由于粉壤土较砂壤土为细质土，土体内部结构更为致密，减弱了入渗过程中浑水泥沙颗粒进入土体内部的滞留作用；另外粉壤土饱和导水率小于砂壤土，因此浑水粉壤土饱和土柱入渗速率更小，泥沙沉积过程受入渗速率影响更小，形成的沉积层也更均匀，综合来看更近于假设条件，因此粉壤土导水率动态模型模拟效果更好。

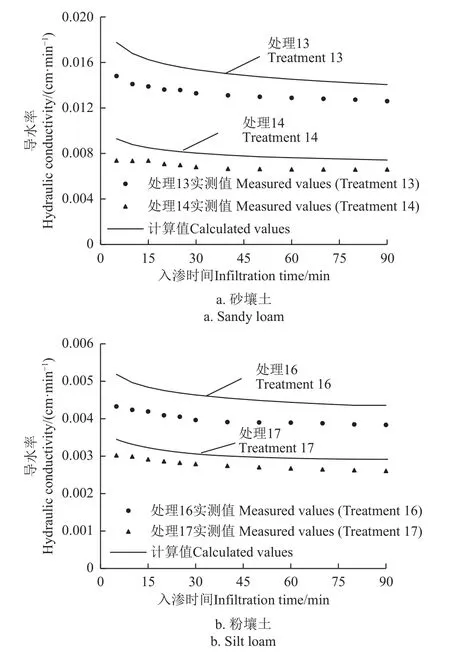
图6 不同处理导水率实测值和计算值Fig.6 Measured and calculated values of hydraulic conductivity for different treatments

3 结论

以土壤质地、含沙率及泥沙种类为影响因素，共进行17 组浑水饱和土柱入渗试验，利用多因素分析法建立和验证了浑水砂土饱和土柱入渗下导水率动态模型，并将此模型推广至砂壤土和粉壤土，得出如下结论：

1）浑水含沙率、黏粒含量和入渗时间对导水率影响极显著（P＜0.01），影响程度由大到小依次为：入渗时间、浑水含沙率、黏粒含量，导水率与浑水含沙率、黏粒含量和入渗时间均为负相关；建立了导水率与各影响因素之间的动态模型，决定系数（R2）为0.853，均方根误差（SRMSE）为0.004 cm/min，模型验证试验结果中模型计算值与实测值的一致性较好，两者间的SRMSE小于0.01 cm/min，相对误差绝对值均值（SMARE）小于7%，说明基于浑水砂土饱和土柱多因素分析法得到的导水率动态模型可靠性较高。

2）导水率变化率随入渗时间的延长逐渐减小，浑水含沙率和黏粒含量对导水率变化率影响显著且影响程度相近，各敏感性指标受入渗时间的影响较大。

3）基于砂土导水率动态模型和假设条件，建立了适用于砂壤土和粉壤土导水率动态模型，砂壤土和粉壤土导水率模型R2分别为0.912 和0.930，SRMSE分别为2×10-3和5×10-5cm/min；模型验证试验结果中模型计算值与实测值的一致性较好，两者间的SRMSE小于0.01 cm/min，SMARE小于17%，表明模型能够较好地反应砂壤土和粉壤土导水率与各影响因素的量化关系。