从一个思想实验看计算思维运用的必要性问题

陈凯 上海市位育中学

历史上，有些思想实验借助逻辑悖论可以推导出令人信服的答案，如伽利略的重力思想实验，有些思想实验中的问题未能获得被普遍认可的解答，但它却成为一种能显现出人的思维方式和局限的特殊工具。

《庄子·杂篇·天下》中提到的“一尺之捶，日取其半，万世不竭”，可看作是一个历史悠久的思想实验。原文指出这是惠施的一个辩题，并说“辩者以此与惠施相应，终身无穷”。人总是能在头脑的想象中将已经取半的捶继续施加以取半的动作，南宋学者洪迈在《容斋随笔》中认为：“虽为寓言，然此理固具。盖但取其半，正碎为微尘，余半犹存，虽至于无穷可也。”持原子不可再分割观点的辩者大概很难说明白，原子所占空间何以是不可再分而取半的。不过，这个“万世不竭”的结论，常让人内心产生出一种找不到终极原因的不安感，大概正是这种不安，使得惠施的辩题常辩不衰。直到现代物理学取得丰富的成果后，人们从微观粒子行为的不确定性与概率特征来加以审视，才发现其实不能用是或否来判定“一尺之捶，日取其半，万世不竭”的命题，与复杂的物理现象相比，落于二边的逻辑思维在此处是苍白无力的。

●用思想实验显现思维方式和局限

本文特意创设了这样一个和计算思维有关的思想实验：某A自认为运用了计算思维解决了某一个问题，如某个需要用枚举法解决的问题，并且，观察某A解决问题过程的某B从某A的行为判定，某A确确实实是运用了计算思维解决了这个问题，那么，假设在后续时间里，某A不断地用同样的方法解决同一类问题，如解决的都是那种能采用枚举法来解决的问题，那么，是不是有理由怀疑，从某个时刻开始，某A不再是运用计算思维，而是依赖某种思维惯性在解决此类问题呢？

为行文方便，姑且将此自创的思想实验称为“褪色的计算思维”，如果将描述中的“计算思维”换成“逻辑思维”（这种替换仍然是思想实验的一部分），即某A自认为且被他人评价为的确运用了逻辑思维解决了某一类问题，而在后续时间内，某A不断遇见这些需要用逻辑思维解决的问题，在这里，似乎就可以说，某A每次解决问题，确实都是运用了逻辑思维。

从“褪色的计算思维”中可以看出这样的问题，如果教师想要借助枚举法的运用创设一个培养和评价计算思维能力的情境和任务，那就要弄明白，学生在面对多个需要借助枚举法解决的问题时，在其不断采用的思维方法中，究竟哪一种的确可以算作是运用了计算思维，显然，不能轻易地说，只要采用了枚举法解决问题就是运用了计算思维，当熟悉了枚举法解决问题的过程后，就只需要拿出已有的应用了枚举法的计算模型或程序代码，运用逻辑思维改变其部分输入数据和输入形式，也一样能解决问题。当某A利用计算思维解决了某一类问题，并且构建了解决问题的模式后，当以后再遇到同类型问题时，计算思维的运用是不必要的。那么，教师应当如何构建一个具有运用计算思维必要性的情境和任务呢？

●一个枚举算法案例引出的关于计算思维的几个问题

有一个逻辑推理趣题是这样的：某推理比赛的冠军是A、B、C、D四位同学中的一位。至于谁是冠军，A说：“不是我。”B说：“是C。”C说：“是D。”D说：“C说的不对。”其中三个人说的是真话，一个人说的是假话，那么到底谁是冠军？

曾有教师在介绍用于计算思维培养的教学案例中提到过这个例子。显然，学生可以通过枚举的方法来判别谁是冠军，在具体操作上，既可以逐个地按不同人说谎的情况进行枚举，也可以逐个地按不同人是冠军的情况进行枚举，通过排除掉存在矛盾的情况，就能得出结论。如果围绕这个案例对培养计算思维进行深入的思考，会引出许多疑惑。

疑惑一：不需要借助枚举，单纯依靠逻辑推理也能解决此问题：由于C和D的说法是矛盾的，所以，说假话的必然是两者之一，然后，如果D说的是假话，则B说的也必然是假话，两个说假话的情况与预设条件不符，所以只能是C说了假话。可见，不借助枚举，也能解决问题。即便说，使用枚举法解决问题体现了计算思维的运用（虽然笔者并不认同这一点），那么，这里其实存在着计算思维运用的必要性的问题。

疑惑二：枚举是人类思维活动中常用的方法，如在图书馆的书架上找出所有的教材、找出某个范围内符合某种特定条件的数字、用穷举的方法构建一个九宫幻方等，所以这里的问题是，用到了枚举法，就一定是运用了计算思维吗？如果非要说人在利用枚举进行逻辑归纳时就运用了计算思维，是不是有一种强行将人的思想降低到机器行为的嫌疑？这里存在计算思维的识别特征的问题，也就是说，要如何将计算思维的运用从人的一般思维的运用中凸显出来。需要考虑当人在利用枚举算法解决问题时，哪些行为是具有可分辨的运用计算思维的特征的。

疑惑三：假设某A在学习了基本的程序语法后，构造了某个算法或某个计算模型，借助枚举法解决了问题。在这种情况下，认为某A的确运用了计算思维解决问题的判定大致是可以得到认可的，但如果有某B直接学习并大致记住了解决此问题的枚举算法，并利用算法解决了此问题，能不能就此认为某B运用了计算思维解决了问题？似乎无法找到证据，认为某B不是依靠对语言的理解（ChatGPT能通过对语言的机器学习来编写枚举算法的程序，能认为ChatGPT运用了计算思维吗？），或是逻辑推理，或是算法思维来解决了问题。这里存在计算思维运用如何判定和评价的问题。虽然一般认为算法思维是计算思维的一部分，但既然提出了计算思维的概念，就应当思考包含了逻辑思维、系统思维、算法思维的计算思维在整体上是如何发挥作用的。

教师在教学设计中，如果要落实计算思维培养的目标，就需要明确计算思维运用何以必要，计算思维运用的特征如何凸显，计算思维运用如何判定和评价这些问题。为了解决这些问题，就有必要对情境和任务本身进行一定的改造。限于篇幅，本文重点讨论计算思维运用何以必要这个问题。

●枚举中的判断问题

不妨做这样的尝试：在教学情境中，任务切入的角度其实并不是怎样解决“谁说假话”的问题，因为，利用枚举法解决此问题，只是日常的逻辑思维的运用而已。相较而言更重要的是，要思考如何构建能实现枚举法的模型，来解决“谁说假话”的问题。需要注意的是，利用枚举法和构造实现枚举法模型这两者间是有区别的。

考虑要设计出某个机器，这个机器能解决部分推理问题，那么，讨论机器如何借助并仅仅借助枚举法解决一系列类似的推理问题，就显现出“机器如何（半）通用性地解决问题”这个有价值的课题。当然，也要同时为其他解决方案预留出空间，如并行搜索、逻辑编程等。围绕机器的行为展开设计而不是借助程序语言环境实现任务目标，就是为了避免学生仅通过语言规则来完成任务。在一项进行中的调查中发现，大部分教师更倾向于在算法和程序设计的教学单元培养计算思维，但在课时有限的情况下，学生通常只能做到学习和应用枚举算法，而不是构建枚举算法，而一旦学生基本掌握了枚举算法，就不再有亲自体验构建枚举算法的可能了。所以，更好的办法是将培养计算思维的平台拓展到信息从采集、编码、处理到应用的整个过程中。

下面，是逐个地按不同人说谎的情况进行枚举，借助涂色和逻辑推理寻求“谁是冠军”答案的方法：绘制4*4的表格，图1是列举出A说谎且其他人不说谎时描述的情况，深绿色代表描述中某人是冠军，浅黄色代表描述中某人不是冠军，未涂色的表示情况不明。第一行是根据A说谎时的描述情况进行纠正后的涂色，第二、三、四行分别是根据B、C、D各人的描述进行涂色。可见，图中有两处矛盾，其一，第一、三列有两处深绿色，说明有两个冠军，产生矛盾。其二，第四列同时有一处深绿色和一处浅黄色，说明某人既是冠军又不是冠军，从而产生矛盾。所以，A说谎且其他人不说谎的情况被排除了。接下来还要分别按B、C、D说谎的情况绘图，这里就不一一展示了。

图1 A说谎时的涂色

即便绘制完成如图1所示的图表，且根据图表做出了A说谎时产生矛盾的推论，这个过程中也只有逻辑思维在起作用，计算思维在哪里呢？不妨更换一下研究角度，问某个机器到底应该如何判断出这种矛盾。这时候就可能涌现出许多不同的解决方案，一种可行的方案是，将不同的颜色用二进制数码加以表征，深绿色设置为“01”，浅黄色设置为“10”，白色设置为“00”。首先，纵向每列按位进行或运算操作，如果得到“11”，则表示存在矛盾。如果以上操作不存在矛盾，则纵向每列按位进行或运算操作，得到四个数值结果，如果存在多个“01”，则表示存在矛盾。

从上述解决方案中可以看出，虽然人能直观看出矛盾所在，但为了让机器判断出矛盾是否存在，就需要构造出一种能够让机器实现判断的方法，这些方法用到了二进制编码和二进制逻辑运算，这正是运用计算机科学的基础概念进行问题求解和系统设计。

这里存在一个疑惑，假设学生没有学习过二进制编码和运算，那么是否就无法运用计算思维来解决这道推理趣题？笔者认为，信息的编码和表征可以有很多种方式，有些方式未必符合当前计算机最有效率的运行方式，但人的创造不应该被现代数字计算机这种已成型的计算装置的工作模式所束缚，创造和想象应当首先不受物理限制，然后再考虑物理现实中的可行性，这个问题留待以后讨论。

●枚举中“下一个”的问题

某个机器要能实现枚举，那么它必然要能做到选取下一个的动作，利用程序语言，当然很容易实现“下一个”，如“for i in range(10)：”这样的语句自然就能从0枚举到9。但和前文所述类似，用程序语言实现这样的“下一个”，不必然运用了计算思维，只要足够熟悉程序语言就能做到，“for i in range(10)：”本身就可以看成是“从10的范围内取出每个数字给i”的人类语言的描述。

仍然以“谁是冠军”为例，图2中列出了枚举所得的所有四种涂色情况，这四种涂色都是由最左面的听众视角变换而来的，变换规律也很简单，分别是第一、二、三、四行的颜色发生变化，如果该行存在深绿色则变为浅黄色，浅黄色则变为深绿色。

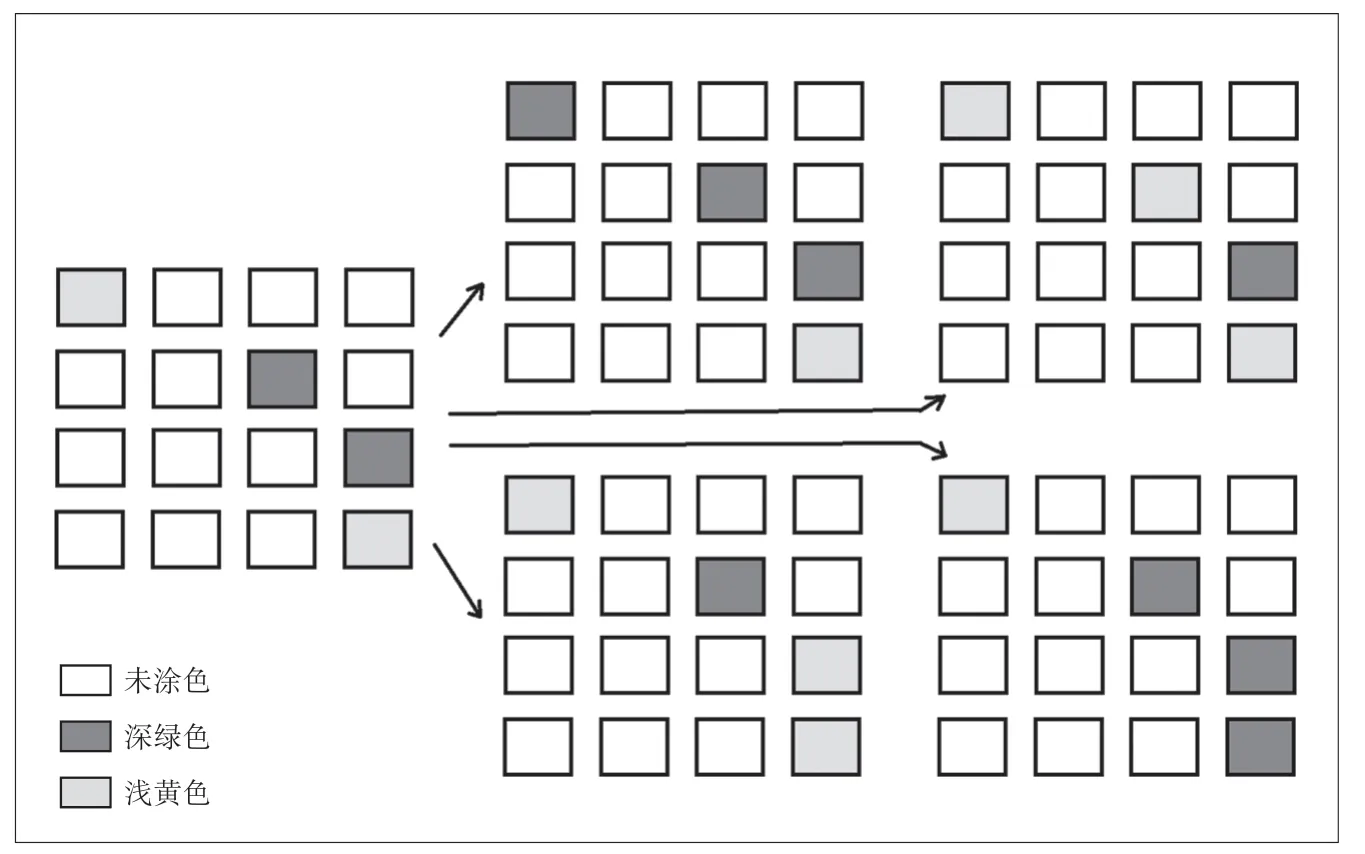
图2 从听众视角涂色变换成四种枚举所得的场景的涂色

从每一行中找到某种颜色进行变换这个动作，本身就是一种枚举，也就是说，为了枚举出每一种说谎的情况，首先要对每一行的每一种颜色进行枚举，这个机器表象的枚举现象和底层的枚举动作其实是不一致的，底层的动作支撑了表象中“下一个”动作的产生。底层的枚举成为高层的实现枚举的计算模型中的一个组成部分，这里再来看“运用计算机科学的基础概念去求解问题和系统设计”这句话，对于“运用计算机科学的基础概念去求解问题”，一方面其有可能与“运用计算机科学的成果去求解问题”相混淆，另一方面有可能让人停留于“运用计算机科学的基础概念在概念层面而不是在计算装置实施计算的层面解决问题”，但如果强调的是“运用计算机科学的基础概念去设计一个系统来求解问题”，那就为什么样的思维方式属于计算思维的运用划定了更精确的界限。

枚举中的“下一步”的可行也隐含了更多低层的原因，那是因为按当前数字计算机的体系结构，读写数据的操作必须遵循一定的指令的顺序，这在计算机实体结构的层面上揭示了在构建计算模型过程中计算思维运用的必要性，在本栏目往期文章《芯中之数—一种展示计算机系统架构工作原理的方法》中对此已有论述，这里不再展开。但如果跳出计算机实体结构的限制，许多计算模型具有并行计算的能力，如DNA计算、量子点计算等，利用这些计算模型实施枚举，就不再有如何实现“下一步”的问题。

●枚举中的停机问题

枚举算法中的“下一步”如何才能停下来，是一个必须面对的问题，也是一个有趣的问题。在高级程序语言中，当循环全部执行完毕后，程序就停了下来，但这是因为有操作系统在管理着程序的运行，程序停下来了，操作系统却并没有停下来。假设不使用普通的计算机，而是用图灵机来解决枚举并将颜色进行变换的问题，如用十进制数1代表二进制数01，用十进制数2代表二进制数10，具体运行规则和运行初始和终止时的状态如下页图3所示，则能发现，图灵机预设了一个停止状态，当读写头遇见空格—也就是没有任何颜色存在的格子时，图灵机就停止运行，但它是怎么停下来的呢？当电路判断到数据符合某种特定的状态时，就执行电路自己断开的动作，这当然是可行的。用函数的递归也能实现当枚举任务完成后自动且自主停机，如果递归函数是一种纯粹抽象的机器，那么递归函数就是其自身的操作系统—虽然现实中，人类构建的递归计算装置都有其物质实体。

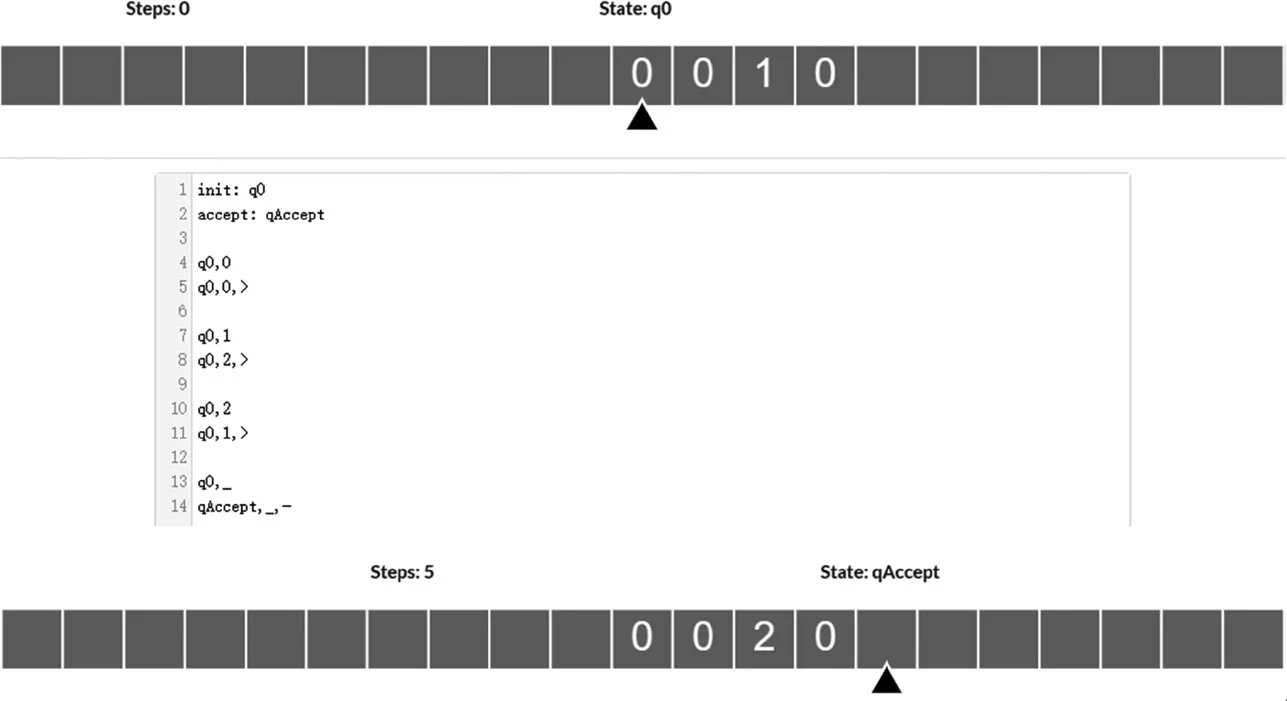
图3 枚举结束后会自己停机的图灵机，上方是初始时的数据，下方是任务完成后的数据

考虑到有学生对函数递归工作过程的理解存在困难，可以思考这样一个演示方案，假设存储器里存储的不仅是数据，也包含对读写头下一步动作的指令，那么机器就不仅能自动根据指令匹配特定数据和替换，还能实现“下一步”动作和适时停机了。图4是一个借助图形化编程工具实现的枚举和自动停机的演示，用表情符号代表机器读写头，用方块代表存储器。在这个例子中，存储器数据中的第一个值代表读写头将要做的动作，0代表右移，1代表停机。而#号后的数据则代表真正的需要被判断或被替换的数值。读写头既从存储器中读取和写入数据，也根据存储器中的数据，来指示下一步将要做的动作。

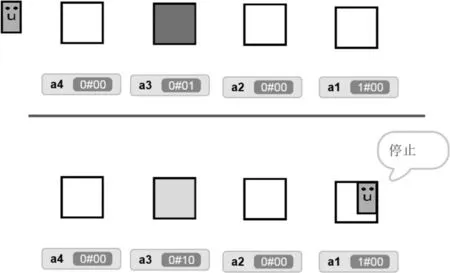
图4 用图形化编程工具演示读写头和存储器的行为