基于自抗扰控制的引信滚转角控制方法

雷泷杰,霍鹏飞,陈 超,高 智

(西安机电信息技术研究所,陕西 西安 710065)

0 引言

二维弹道修正引信是无控弹药低成本精确化改造的最佳技术途径,弥补了精确制导弹药和无控压制弹药间的空白[1]。仅通过将弹丸头部传统引信更换为二维弹道修正引信,传统无控弹药便可实现对小幅员目标的精确打击(CEP一般不大于30 m)。国际上主流的二维弹道修正引信方案有两种[2],固定舵方案(代表产品为美国ATK公司PGK引信)和可动舵方案(英国BAE公司“银弹”引信和以色列IAI公司的TopGun引信)。两种方案均通过修正控制执行机构减旋后的倾斜转弯(BTT)方式控制引信滚转角实现对弹丸原有弹道的二维(射程和横偏两个方向)修正,引信滚转角控制品质直接影响到弹道修正控制精度,进而体现在对目标的精确打击水平。

目前滚转角控制通常采用的方法有PID控制[3]、变结构控制[4]以及最优控制[5]等现代控制方法。在实际二维弹道修正引信飞行过程中,引信受到的轴向摩擦力矩以及由于弹道变化及姿态扰动带来的气动干扰力矩影响,其模型参数在一定范围内发生变化,尤其是在飞行末段弹丸稳定性降低、动压增大、气流角变化加剧时,文献[3]采用的PID控制通过参数分段整定方式来克服模型参数扰动,当模型存在较强非线性时,该方法得到的控制精度难以有效保障。文献[4]采用的变结构控制存在同样类似的问题,同时控制系统容易出现震荡。文献[5]采用最优控制等现代控制方法对模型依赖程度过高,使其很难在短时间内应用于武器系统当中。文献[6]提出了一种基于模型补偿的弹体滚转角自抗扰控制方法,该方法在误差模型易获取情况下具有较好控制效果,但对于二维弹道修正引信而言,干扰模型多元化且不易获取。本文针对如何有效估计弹丸飞行过程中二维弹道修正引信受到的轴向摩擦力矩以及气动干扰力矩并对其进行补偿以实现引信滚转角的高精度控制问题,提出一种基于自抗扰控制的引信滚转角控制方法。

1 滚转角运动数学模型及自抗扰控制理论

1.1 二维弹道修正引信滚转角运动数学模型

弹丸在飞行过程中,对于二维弹道修正引信滚转通道而言,引信滚转角运动主要受到作用在与引信滚转姿态控制系统执行机构相连的导转翼面的气动导转力矩,通过减旋机构传递的来源于弹丸与引信头部相对旋转产生的耦合力矩,弹丸飞行过程中气流角变化引起的气动扰动力矩。对于固定舵和可动舵两种方案(见图 1和图 2)而言,仅耦合力矩产生方式不同。固定舵方案中的耦合力矩来源于主动电磁控制力矩以及翼面与弹丸之间的轴承摩擦力矩,可动舵方案中的耦合力矩来源于引信和弹体双旋产生的减旋机构轴承摩擦力矩。

图1 固定舵方案,代表产品为美国ATK公司PGK引信Fig.1 Fixed-canard technology,represented by PGK of ATK company

图2 可动舵方案,代表产品为英国BAT公司“银弹”引信和以色列IAI公司“TopGun”引信Fig.2 Movable canard technology,represented by “Silver Bullet”fuze of British BAE company and “TopGun”fuze in Israeli IAI company

引信绕其纵轴转动的动力学以及运动学非线性微分方程组如式(1)所示[6]。

(1)

1.2 自抗扰控制理论

自抗扰控制是利用“基于误差来消除误差”基本控制策略,与现代控制理论及方法相结合,通过估计并补偿控制系统不确定因素的新型实用控制技术[7]。自抗扰控制技术发扬并丰富了PID控制思想精髓,从根本上克服了PID控制的局限性[8]：

1) 要求缓变的输出变量跟踪跳变的控制目标是不合理的;

2) 误差的微分信号不好提取,易受噪声影响;

3) P、I、D的线性组合不是最优的组合方式;

4) 误差积分I的引入带来很多副作用,如使闭环控制系统变得迟钝、产生震荡等。

通过以下策略有效解决了PID控制存在的上述缺陷：

1) 安排控制目标的“过渡过程”;

2) 使用跟踪微分器提取“微分”;

3) 寻找合适的非线性组合;

4) 使用扩张状态观测器来估计总扰动。

自抗扰控制系统基本原理框图如图 3所示。

图3 自抗扰控制系统基本原理框图Fig.3 The basic principle block diagram of the ADRC

3 引信滚转角自抗扰控制器

二维弹道修正引信滚转角控制的目的是使得引信滚转角γ跟踪滚转角控制指令γc,即要求引信滚转角与滚转角控制指令误差为零。按照上述自抗扰控制理论设计引信滚转姿态控制器。

1) 利用最速跟踪微分器为引信滚转角控制指令安排二阶过渡过程。

选取状态x*=[γ*ω*]T,建立式(2)所示的最速跟踪微分器。

(2)

式(2)中,r为最速跟踪微分器参数。

2) 利用最速跟踪微分器对测量得到的引信滚转角进行平滑滤波,选取状态x*=[γ0ω*]T,建立式(3)所示的最速跟踪微分器。

(3)

式(3)中,r0为最速跟踪微分器参数,γ为引信滚转角,状态γ0即为引信滚转角滤波输出值。

3) 在扩张状态观测器数学模型中体现引信滚转运动过程中轴向摩擦力矩以及气动干扰力矩等总扰动状态的微分项引入滚转角速度影响,得到更准确的状态观测值。

构建式(4)所示的非线性扩张状态观测器。

(4)

(5)

4) 采用式(6)所示的非线性组合误差反馈律

u0=-fhan(e1,e2,r*,h),

(6)

式(6)中,u0为中间控制计算量,e1和e2分别为过渡过程跟踪微分器输出的状态滚转角及滚转角速度指令与状态观测器状态z1和z2的差值,r*为最速控制综合函数fhan(具体表达式见式(7))的参数,h为系统控制周期。

(7)

(8)

采用上述方法可基于自抗扰控制理论实现对引信滚转角控制指令的准确跟踪。自抗扰控制稳定性分析可参考文献[7],这里不再详细讨论。

3 仿真验证

采用Matlab中Simulink工具箱(正版已授权)按照本文给出的引信滚转角自抗扰控制器设计方法建立了Simulink仿真模型,如图 4所示。基于155 mm榴弹平台1.2Ma对应的飞行弹道环境,对二维弹道修正引信滚转角控制系统进行了仿真,引信滚转角初始状态为0°,滚转角控制指令为180°,仿真步长0.001 s。二维弹道修正引信滚转角控制系统会存在各种误差和干扰,主要包括滚转角及滚转角速度测量误差、摩擦力矩散布误差以及由于气象环境变化或弹丸气流角的变化而引起的气动干扰误差。表1给出了弹丸在实际飞行过程中主要误差源及参考值,将其引入仿真模型中,分别采用变结构控制器和自抗扰控制器进行仿真,仿真结果如表 2、图 5和图 6所示。

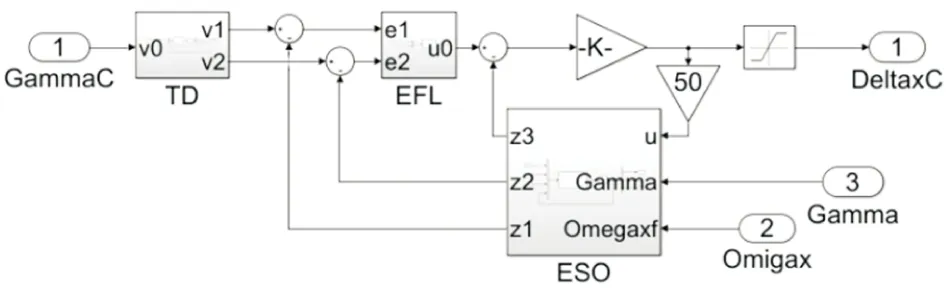
图4 自抗扰控制器Simulink仿真模型Fig.4 Simulation model of ACRC controllor

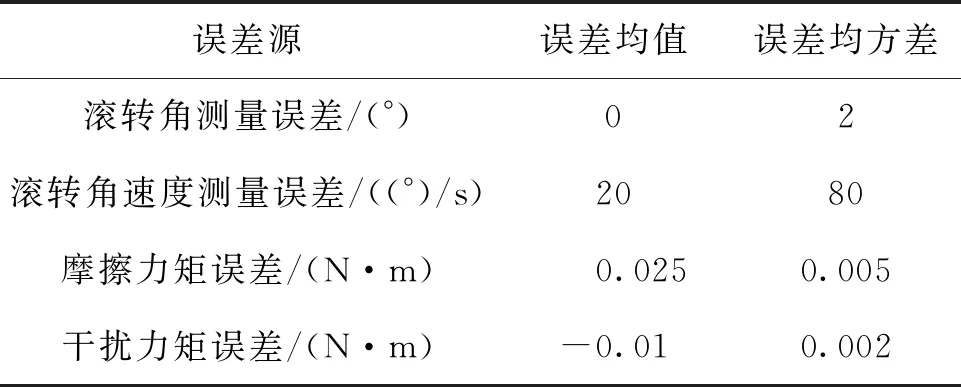
表1 二维弹道修正引信滚转角控制仿真误差源Tab.1 Simulation error resources of roll angle control system on 2-D trajectory correction fuze

表2 二维弹道修正引信滚转角控制仿真统计结果Tab.2 The analytical results of roll angle control system on 2-D trajectory correction fuze

图5 引信滚转角变化曲线Fig.5 Simulation diagram of roll angle control system on 2-D trajectory correction fuze

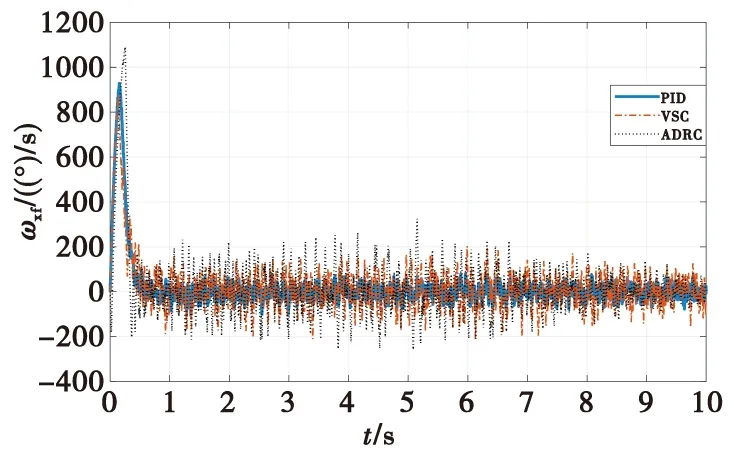
图6 引信滚转角速度变化曲线Fig.6 Simulation diagram of roll angle rate control system on 2-D trajectory correction fuze

当引入表1中测量及扰动误差时,从表2的调节时间可以看出,由于摩擦力矩干扰,采用PID控制器时出现超调,持续时间约1.5 s,而采用变结构控制与自抗扰控制器时均未出现类似现象,这进一步说明变结构控制器与自抗扰控制器抵抗外界扰动的鲁棒性较强。同时从稳态误差中可以看出,采用自抗扰控制器控制精度优于采用变结构控制器的结果,再次验证了自抗扰控制器能够有效估计不确定性并通过引入控制量来对其进行补偿的基本原理。

4 结论

本文提出一种基于自抗扰控制的引信滚转角控制方法。该方法基于自抗扰控制理论,通过引入引信滚转角速度和增加滚转角跟踪微分滤波的扩张状态观测器模型,实现对引信滚转运动过程中受到的轴向摩擦力矩以及气动干扰力矩的准确估计,通过总扰动状态量化描述并反馈至控制回路进行相关补偿计算,实现引信滚转角的稳定控制。仿真结果表明,这种基于自抗扰控制的引信滚转角控制方法能够有效估计弹丸飞行过程中二维弹道修正引信受到的轴向摩擦力矩以及气动干扰力矩并对其进行补偿,最终实现引信滚转角的高精度控制,与经典PID控制和变结构控制相比,鲁棒性更强,工程实现简单,能够满足更高滚转角控制精度需求。