列二元一次方程组解答实际问题的方法
胡媛
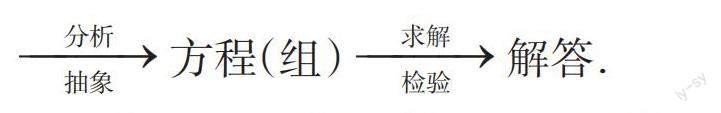


二元一次方程组是刻画现实世界的数学模型,与现实世界有着十分密切的关系.用二元一次方程组解答实际问题的一般方法是根据具体问题中的数量关系列出二元一次方程组,求解并检验所得结果是否符合实际意义.这对同学们分析问题和解决问题的能力有较高的要求.对此,笔者总结了列二元一次方程组解应用题的基本思路和步骤,并结合具体的例题展开分析,希望对同学们掌握这一方法有所帮助.
一、列二元一次方程组解答实际问题的基本思想和步骤
列方程解实际问题,是把“实际问题”抽象为“数学问题”,把“未知”转化为“已知”的思想方法的应用.它的关键是把已知量和未知量联系起来,找出题目中的等量关系建立方程组求解.
一般说来,有几个未知量就列出几个方程,所列方程必须满足:
(1)方程两边表示的是同类量;
(2)同类量的单位要统一;
(3)方程两边所表示的数量关系要相等.
列二元一次方程组解答实际问题,关键在于找出问题中的等量关系列方程组,求出方程组的解后,要注意检验解是否符合实际意义.这个过程可以表述如下:實际问题
在这个过程中,分析和抽象的步骤是正确列出方程组的关键,它通常包含以下三步:
(1)借助示意图、表格等弄清题意和其中的数量关系,用字母表示适当的未知数;
(2)找出能表示问题含义的等量关系;
(3)对等量关系中涉及的量,列出需要的式子,进而列出方程组.
二、二元一次方程组在解答实际问题中的具体应用
1.列二元一次方程组解答产品配套问题
生活中的配套问题很多,如课桌和板凳、电扇叶片和电机的配套等.各种配套问题都有一定的数量比例.列二元一次方程组解答产品配套问题时,关键就要弄清配套产品中哪种数量多,哪种数量少,以及它们是几比几的配套比例关系.只有这样才能把已知量和未知量联系起来,正确找出题设中的等量关系,列出方程组.
例1 某工厂加工螺栓、螺帽,已知每1块金属原料可以加工成3个螺栓或4个螺帽(说明:每块金属原料无法同时既加工螺栓又加工螺帽),已知1个螺栓和2个螺帽组成一个列二元一次方程组解答实际问题的方法零件,为了加工更多的零件,要求螺栓和螺帽恰好配套.若把26块相同的金属原料全部加工完,问加工的螺栓和螺帽是否恰好配套?若恰好配套,请求出加工螺栓和螺帽各需要的金属原料块数,若不是恰好配套,请说明理由.
分析:设把 x 块金属原料加工成螺栓, y块金属原料加工成螺帽正好配套,根据共26块相同的金属原料且加工的螺帽数量是螺栓的2倍,即可得出关于 x,y 的二元一次方程组,解之即可得出 x,y 的值.结合 x,y 为整数可得出加工的螺栓和螺帽不是恰好配套.
解:设把 x 块金属原料加工成螺栓, y 块金属原料加工成螺帽正好配套,依题意,得:
∵ x,y 应均为整数,
∴加工的螺栓和螺帽不是恰好配套.
2.列二元一次方程组解答年龄问题
年龄问题往往是和差问题、倍数问题的综合应用.解答此类问题首先要明确两个人年龄的增长数相等,不管时间发生怎样的变化,每人的年龄都在增长,但是他们之间的年龄差始终不变. 因此,同学们在解题时一定要把握年龄差不变这个解题关键点来建立等量关系.
例2 聪聪在给妈妈过生日时发现自己的年龄与妈妈的年龄的十位数字与个位数字正好相反,他同时还发现,过10年,妈妈岁数减1(岁)刚好是自己岁数加1(岁)的2倍;再过1年,他们两人的年龄又一次相反,且十位数字与个位数字的和为7,你能知道聪聪和他妈妈现在的年龄吗?
(1)设未知数,用代数式表示聪聪和他妈妈的年龄;
(2)列方程解答.
分析:(1)设聪聪的年龄为(10x+y)岁,由聪聪的年龄与妈妈的年龄的十位数字与个位数字正好相反,可得出妈妈的年龄;(2)根据“过10年,妈妈岁数减1(岁)刚好是自己岁数加1(岁)的2倍;再过1年,他们两人的年龄又一次相反,且十位数字与个位数字的和为7”,即可得出关于 x,y 的二元一次方程组,解之即可得出结论.
解:(1)设聪聪的年龄为(10x+y)岁,则妈妈的年龄为(10y+x)岁.
(2)根据题意得:
答:聪聪今年14岁,妈妈今年41岁.
3.列二元一次方程组解答行程问题
行程问题主要包括相遇问题与追及问题.在相遇问题中,两人所走的路程和等于两地距离;在追及问题中,快的路程加上慢的路程等于两地距离.这些是列方程时常用的等量关系.在列代数式时常用以下数量关系:时间×速度=路程,时间=路程÷速度,速度=路程÷时间,顺水速=静水速+水流速,逆水速=静水速-水流速等.
例3 甲乙两地相距240千米,一辆小车和一辆摩托车分别从甲、乙两地同时出发相向而行,1小时20分两车相遇.相遇后,摩托车继续前进,小车在相遇处停留1个小时后调头按原速返回甲地,小车在返回后半个小时追上了摩托车.
(1)求小车和摩托车的速度;
(2)求相遇后,摩托车继续行驶多少小时两车相距30千米?
分析:(1)小车的速度为 x 千米/时,摩托车的速度为 y 千米/时,利用路程=速度×时间,结合两车速度间的关系,可得出关于 x,y的二元一次方程组,解之即可得出小车和摩托车的速度;(2)设相遇后,摩托车继续行驶m 小时两车相距30千米,利用路程=速度×时间,结合两车相距30千米,可得出关于 m的一元一次方程,解之即可得出结论.
设小车的速度为 x 千米/时,摩托车的速度为 y 千米/时,
三、列二元一次方程组需注意的几点
1.不能用同一个等量关系列两个方程联立成方程组,这样在解方程组时会出现0=0的情况,求不出未知数的值.
2.对于涉及的数量关系较复杂,一时难以找到等量关系的问题,可借助列表或画图的方法,把题中的数量和等量关系挖掘出来.若是新型题,还要结合生活实际,以找到解题的突破口.
3.对于求得的方程组的解,必须检验它是否符合实际意义或题意.

