运动模糊图像的模糊参数快速估计方法研究*
罗锦晖 丁 超 朱杰凡
(武汉数字工程研究所 武汉 430205)
1 引言
运动模糊失真是生活中最常见的图像失真类型,对运动模糊图像进行复原最重要的一步就是求运动模糊图像的模糊参数,根据该模糊参数即可对图像进行复原。近年来,已经有多种方法应用于运动模糊参数的检测与图像复原领域,可以较为准确地鉴别出模糊角度与模糊尺度的大小。但是这些方法均聚焦于降低模糊参数的估计误差,对算法的运行时间不够重视,不能实现模糊图像的快速恢复。本文基于频谱图像上进行Radon 变换的方法,通过设置兴趣区域和调整计算步长的方式,降低了算法计算量,此方法与以往的鉴别方法相比,计算时间有较大程度的降低,检测精度较高。
2 运动模糊图像模型
经典的图像退化模型[1]如图1 所示。其中f(x,y)、h(x,y)、g(x,y)、n(x,y)分别是原始图像、运动模糊函数[3](Point Spread Function,PSF)、运动模糊图像以及加性高斯白噪声。当模糊系统是空间线性移不变系统时,则可以将退化模型用如下的数学式表达:

图1 图像退化模型

图2 鉴别曲线

图3 模糊角度估计图像
其中“*”为线性卷积运算符。
如果运动模糊方向已知,对运动模糊图像进行坐标旋转变换,使模糊方向成水平方向,此时式(1)可以简化为
假设图像退化过程除受相对运动之外,不存在散焦等其他因素的影响。图像f(x,y)沿x 方向做匀速直线运动,运动模糊尺度为d,则点扩展函数h(x,y)可近似表示为一个窗函数,表达式如下:
而针对其他方向的运动模糊算子[4~5],可将水平方向运动模糊算子旋转θ(-90°≤θ≤90°)角(逆时针为正,顺时针的负)即可得到。
3 典型运动模糊图形参数鉴别算法
在大量的运动模糊图像角度参数[6~8]的研究中,对图像进行傅里叶变换,研究图像在频域下的特性是较为常用的方法。
对式(1)进行傅里叶变换,可以得到图像退化过程中的频域描述,如式(4)所示:
其中G(u,v),F(u,v),H(u,v),N(u,v)分别为运动模糊图像、运动模糊函数、原始图像以及噪声的傅里叶变换。在不考虑噪声的情况下,则图像退化的过程可以如式(5)所示:
在此基础上,设图像退化时的过程为匀速直线运动,则运动模糊图像可表示为
对上式进行傅里叶变换可得
其中x0(t),y0(t)为图像在t时间内分别在x和y方向上的变化量,T 为图像曝光时间。由式(5)和式(7)可知:
若图像在时间T 内在x 和y 方向上移动的距离分别为a和b,带入上式可得:
在图像尺寸M×N的条件下,则有
若将图像的运动模糊角度定义为与x 轴正向的夹角,则有tan(θ)=b/a,带入上式可知运动模糊角度:
由上式可知,根据频谱条纹角度与图像尺寸可以计算出图像的运动模糊角度。
模糊尺度[9]的估计通常是在已知模糊角度的基础上,将图像进行旋转使模糊方向水平,对旋转后的图像进行微分,得到微分图像,再对微分图像进行自相关计算[11],将自相关的结果每列相加,得到鉴别曲线[10]。简单的鉴别曲线如下图所示,曲线在0 点处相关程度最大,呈现出零频峰值,在图像模糊的边缘位置相关程度最小,呈现出最小值,并分布在最大值两侧,图像模糊尺度的大小即为负峰值之间距离的一半。
4 改进的运动模糊图形参数快速估计算法
4.1 模糊角度估计
本文采用基于Radon变换[2]的方法计算运动模糊图像频谱条纹[13]的方向角。Radon 变换是沿着不同的直线对图像做线积分,直线与图像中心的距离为d,方向角为θ,具体计算公式如下:
由于图像频谱图中存在一组倾斜的亮条纹[12],沿该倾斜方向上的积分值最大,故通过Radon 变换求最大值便可知运动模糊方向角,模糊图像的频谱图[14~15]和Radon 变换图像如下图所示。由于Radon变换计算量较大,严重影响了计算速度,考虑到运动模糊图像在所有位置模糊程度基本相同的情况,本文采用了保留部分图像,缩小区域进行计算的方式,并在倾斜方向角的步进方面作了优化,基于获得最少计算量的情况得到计算倾斜角的步进长度为10,实验结果表明该方案能极大降低程序运行时间,在倾斜角计算的准确度方面与原方法比较没有明显差距。
4.2 模糊尺度估计
本文对模糊尺度的估计是在计算出模糊角度的基础上,将运动模糊图像的频谱图像旋转相应的角度并二值化,由于当不为0 时H(u,v)=0,此时频谱图像呈现出暗条纹,根据各暗条纹之间的距离即可得到模糊尺度,计算公式如下:
L 为模糊尺度,N 为图像宽度,d 为相邻暗条纹之间的距离。由于频谱图像中中心亮条纹两侧的暗条纹相隔距离为2d,本文直接从频谱图像的中心位置出发寻找最近的暗条纹,只需要一半的计算量,降低了计算时间。
5 实验结果与分析
为验证本文提出的方法对运动模糊图像参数估计的高效性及准确性,选用了模糊尺度10~50,模糊方向0°~180°,像素658×411 的若干模糊图像,将本文实验结果与经典算法的结果比较,如表1~2所示。

表1 模糊角度估计结果
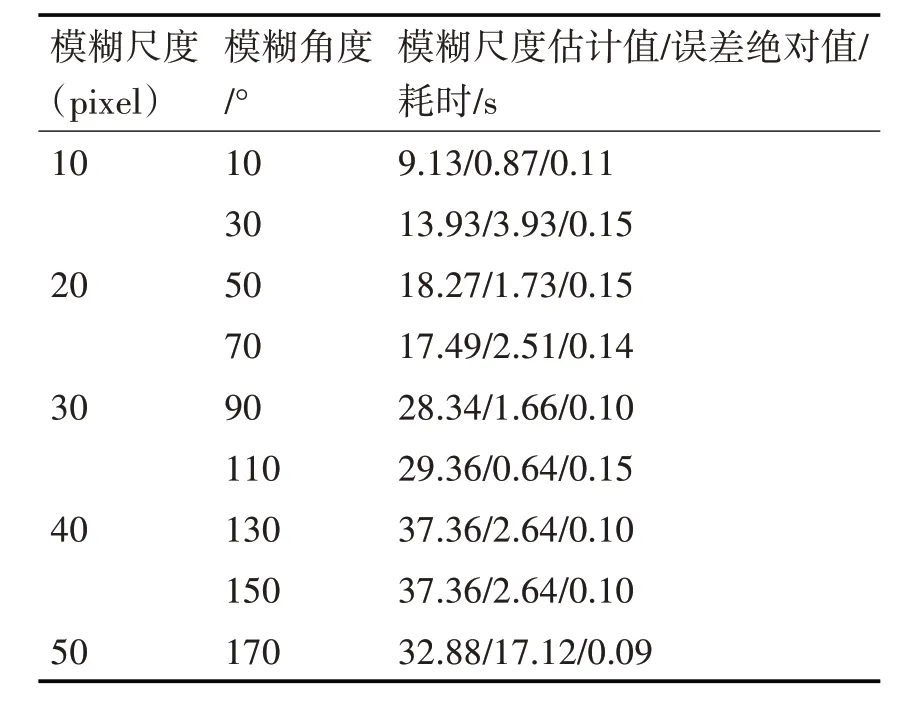
表2 模糊尺度估计结果
6 结语
本文对运动模糊图像的模糊参数进行研究,提出了一种改进的模糊参数快速估计算法。实验结果表明,本文方法在计算时间上相比传统算法有了极大提高,并在模糊参数估计的准确度上没有明显降低,说明了本文方法的有效性。

