单轴静压条件下高压多层陶瓷电容的容值变化
刘波,杨荷,赵慧,吴学星,李华梅,程祥利
(中国工程物理研究院 电子工程研究所,四川 绵阳 621999)
0 引言
高压多层陶瓷电容(简称高压陶瓷电容)为爆炸箔冲击片起爆系统的关键器件,用于起爆系统的储能、点火等方面。高压陶瓷电容容值的稳定性对起爆系统的稳定性起关键作用。在炮射、侵彻等应用场景中,高压陶瓷电容会受到很强的外力作用,其在高偏置电场(107V/m量级)[1]、施加力场(101MPa量级)[2]的容值变化特性将决定起爆系统能否正常实现其功能。要分析高压陶瓷电容在高压、动态作用力下的容值变化,需掌握高压陶瓷电容在高压、静态作用力下的容值变化。
针对外力对于电容参数的影响方面,李长龙等[3-4]、Teverovsky[5-6]分析钽电容在外力作用下的性能变化。对于高压陶瓷电容,Daniel等[7]、程向群等[8]通过高冲击试验测试了高压电容的工作特性,但并未给出定量结论与参数漂移原因。Yang等[9-10]、Wang等[11]以低压陶瓷电容为研究对象,通过构建唯象热力学模型分析了外力作用下材料介电性能和电容容值的变化。
虽然对于陶瓷电容在外力作用下的容值变化已有部分研究,但对于高压陶瓷电容在高偏置电场(107V/m量级)、施加力场(101MPa量级)的容值变化机理较少,多数为定性的试验现象,缺乏内在的变化机理研究。本文研究首先通过唯象热力学模型分析了材料在高偏置电场条件下,其介电性能随压应力、拉应力的变化规律;进一步综合试验结果与有限元仿真结果,分析高压陶瓷电容的容值变化机理,为高压陶瓷电容在更加复杂环境条件下的适应性分析与设计提供重要的指导作用。
1 高压陶瓷电容的结构特征
高压陶瓷电容的外观结构如图1所示,高压陶瓷电容主要由内电极、端电极及介质材料等部分组成。高压陶瓷电容的电极材料为Ni,介质材料为以BaTiO3为主的复合掺杂材料[12-13]。

图1 高压陶瓷电容外观结构示意图[12-13]Fig.1 Structure diagram of high-voltage ceramic capacitor[12-13]
单个电容容值主要受层间距、介质材料的介电性能等方面的影响。常温(20 ℃)下Ni与BaTiO3材料参数如表1[14-15]所示,根据电极材料与介质材料的弹性模量,在1 GPa的表面压力作用下,材料的变形不足1%,因此可以看出外力对于电容层间距的影响十分有限。从高压陶瓷电容的结构可以看出,高压陶瓷电容可以看做数个平行板电容并联而成。当在端电极间施加千伏级别高电压时,内部每个电容的微米尺度内电极间电压均为千伏级别,内部场强将高达107V/m。而电容内部介质材料BaTiO3为铁电材料,内部高场强将影响材料的介电性能进而影响电容的容值。
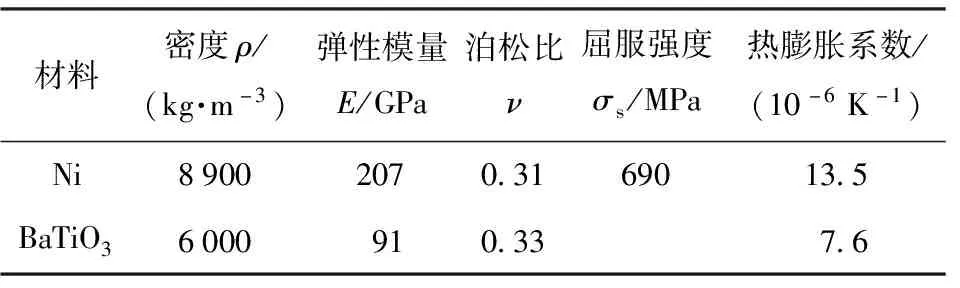
表1 内电极与介质材料的材料参数[14-15]Table 1 Material parameters of the electrode and dielectric material[14-15]
2 外力作用下电容介质材料的介电性能分析
为分析介质材料自发极化引起的自由能,文献[16-17]将Devonshire提出的唯象热力学模型中使用的系数进行了修改,引入了序参量的8次方项,并考虑到了沿3个主轴方向上的极化强度分量,从而得到式(1)所示的吉布斯自由能F(P)的表达式。由于片式多层陶瓷电容器(MLCC)中的介质材料是少量掺杂的BaTiO3陶瓷,少量掺杂的存在不会对纯BaTiO3陶瓷的自由能造成很大影响,因此为简化起见,在建立唯象热力学模型时,可以把它近似看成纯BaTiO3陶瓷。
(1)
式中:P1、P2、P3分别为3个正交主轴方向上自发极化强度;α为不同晶相间的相变系数;T为温度。为分析带电状态下外力对高压陶瓷电容介电性能的影响,引入由外部应力场引起的弹性能和和偏置电场引起的静电能得到吉布斯自由能ΔG(P)的表达式为

(2)
式中:Sij和Qij分别为弹性柔顺系数和电致伸缩系数;σi为应力分量;Ei为电场强度分量。根据式(2)求解材料的介电常数,先求得吉布斯自由能的最小值及相应的自发极化强度,然后求解介电常数。式(1)与式(2)中的吉布斯自由能的相关系数如表2[18]所示。

表2 吉布斯自由能的相关系数[18]Table 2 Coefficients of Gibbs free energy[18]
本文主要研究高压陶瓷电容在高压带电状态下,电容受平行于内电极方向的压力FT及垂直于内电极方向的压力FN作用时,电容的介电性能随外部力场的变化,如图2所示。

图2 高压陶瓷电容施加外力示意图Fig.2 Force diagram of high-voltage ceramic capacitor
2.1 外部力场平行于内电极方向时
压力FT平行于内电极,即垂直于内部自发极化方向时,由于Ni电极的弹性模量明显高于BaTiO3介质材料的弹性模量,平行于电极方向的压力使内电极弯曲,在介质材料产生面内张应力,并在相应方向出现自发极化,则内部介质材料的极化强度、电场强度及应力状态分别为
P1=P2=0,P3=P≠0
σ1=σ2=0,σ3=σ>0
E1=E2=0,E3=E≠0
(3)
根据式(2),材料吉布斯自由能表达式为

(4)
首先通过数值方法求得自由能最小值及相应的自发极化强度P,即
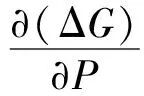
(5)
将求解得到的极化强度P代入式(4),则介质材料的介电常数为
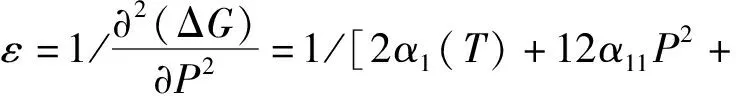
(6)
式中:ε0为真空介电常数,ε0=8.85×10-12F/m。
一般高压陶瓷电容的内电极间距为50~75 μm,本文爆炸箔冲击片起爆系统的电压为1 500 V,因此高压陶瓷电容的电场强度为20~30 MV/m。通过式(4)、式(5)、式(6)计算得到内部偏置电场分别为20 MV/m、22 MV/m、25 MV/m、27 MV/m、30 MV/m时,介质材料在0~200 MPa张应力作用下介质材料的相对介电常数变化,如图3所示。
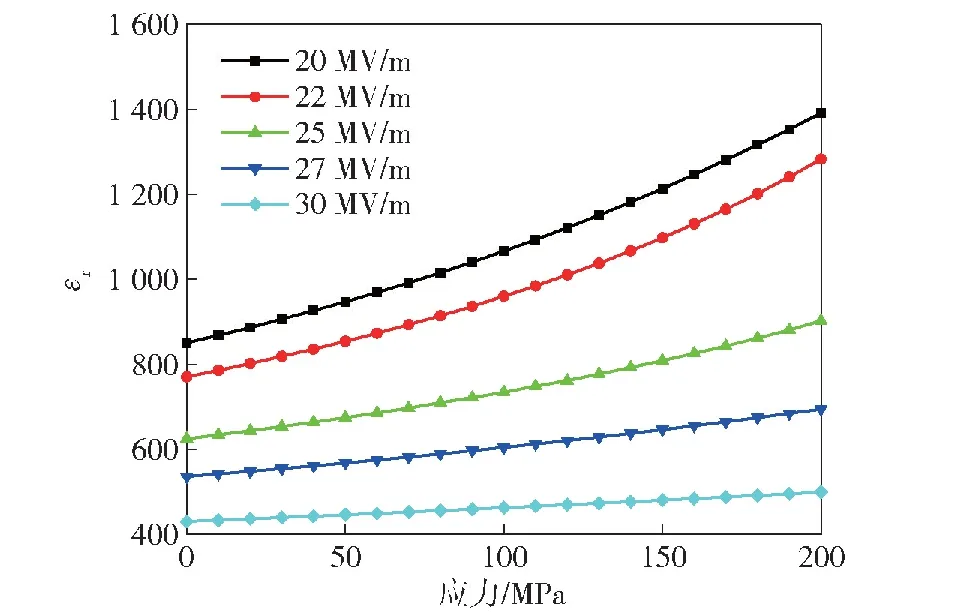
图3 介质材料的相对介电常数随张应力的变化Fig.3 Variation of relative dielectric constant of the dielectric material with tensile stress
从图3中可以看出:在平行于内电极方向的压力FT的作用下,介质材料内部将产生张应力,介质材料的相对介电常数增加,造成这一现象的原因是平行于内电极方向的压应力将推动介质材料中铁电畴壁的运动,进而增加了畴壁的运动对介电效应的影响[19];随着偏置电场强度的提高,电场对铁电畴壁的运动起主导作用,外部应力对于铁电畴壁的推动作用减弱,进而造成张应力对于材料相对介电常数的提升作用降低。
2.2 外部力场垂直于内电极方向时
压力FN垂直于内电极,即平行于内部自发极化方向时,因内电极与端电极的约束,垂直于内电极的作用力在介质材料产生面内压应力,并在相应方向出现自发极化,则内部介质材料的极化强度、电场强度及应力状态为
P1=P≠0,P2=P3=0
σ1=σ<0,σ2=σ3=0
E1=E≠0,E2=0,E3≠0
(7)
根据式(2),材料吉布斯自由能表达式为

(8)
同样地,通过式(5)、式(6)是可以得到内部偏置电场分别为20 MV/m、22 MV/m、25 MV/m、27 MV/m、30 MV/m时,介质材料在0~200 MPa压应力作用下介质材料的相对介电常数变化,如图4 所示。

图4 介质材料的相对介电常数随压应力的变化Fig.4 Variation of relative dielectric constant of the dielectric material with compressive stress
从图4中可以看出,在垂直于内电极方向的压力FN的作用下,介质材料的相对介电常数减小。造成这一现象的原因是:垂直于内电极的方向实际同样平行于内部电场方向,该方向的应力将进一步增强内部电场对于铁电畴壁的夹持作用[20],进而影响铁电畴壁的运动与翻转,最终影响材料的介电性能。
3 试验样品与试验方法
为更加深入分析高压陶瓷电容在带电状态下外部力场对于其容值的影响,采用万能材料试验机对高压电容进行静态压缩,分别从平行于内电极的方向、垂直于内电极的方向施加作用力,并在压缩过程中采用电桥盒测试高压陶瓷电容的容值。
3.1 试验样品
试验样品标称容量为404 nF,额定电压为1 500 V。高压陶瓷电容的长度、宽度、厚度分别为17.0 mm、15.0 mm、4.0 mm,如图5所示。静态压缩试验分别从高压陶瓷电容的长度方向(如图2中的1轴方向,即平行于内电极的方向)、厚度方向(如图2中的3轴方向,即垂直于于内电极的方向)对电容施加作用力。
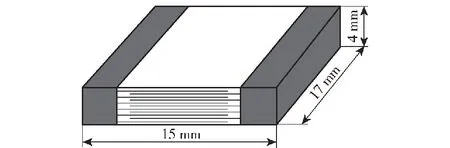
图5 高压电容试验件示意图Fig.5 Schematic diagram of capacitor test piece
如图6所示,高压陶瓷电容样品两个内电极内端间距为130 μm,外端间距为150 μm,则电容内部电极间距为60 μm,内电极厚度为10 μm。高压陶瓷电容样品的电压为1 500 V,内部电场强度为25 MV/m。

图6 高压电容断面局部图Fig.6 Partial section of high-voltage capacitor
如图7所示,采用硅橡胶导线连接高压陶瓷电容的引脚,进而对高压陶瓷电容施加高电压与电容参数测试。为保证高压陶瓷电容与万能材料试验机压头的绝缘,采用聚四氟乙烯薄膜在高压陶瓷电容表面做2层包覆。试验一共准备6块高压陶瓷电容样品,3块用于平行于内电极方向,如图7(a)所示,3块用于垂直于内电极方向,如图7(b)所示。

图7 高压电容试验样品Fig.7 Test pieces of the high-voltage capacitor
3.2 试验方法
常温条件(20 ℃)下,通过万能材料试验机对高压陶瓷电容样品进行加载,压缩过程中样品与试验机压头接触面均匀受力,通过压头上的力传感器测试得到的力来计算样品接触面承受的压力,如图8所示。
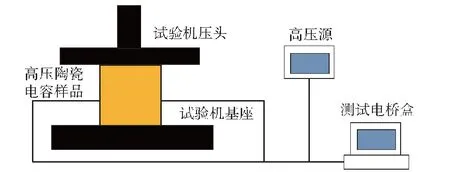
图8 压缩试验示意图Fig.8 Schematic diagram of compression test
试验过程中,电容放置于材料万能试验机夹具中间,每隔5 min加大一次压力,直到电容破损,施加的压力如表3所示。
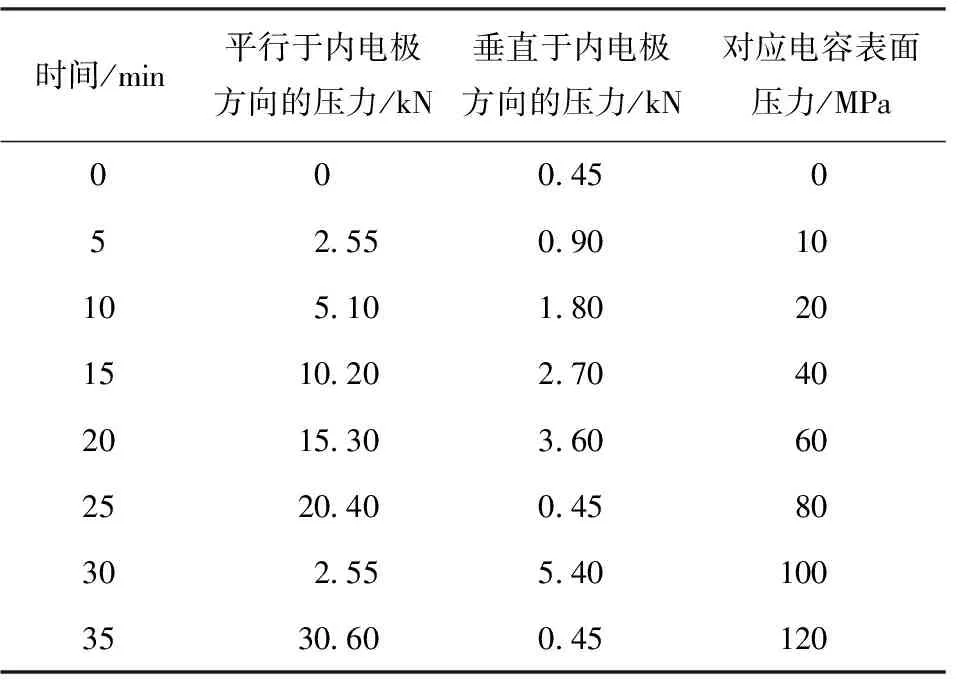
表3 不同方向施加的压力历程Table 3 Histories of stress applied to capacitor from different directions
加载过程中,通过高压源对电容两端施加1 500 V的高电压。通过测试电桥盒对压缩过程中电容的容值进行测试,测试得到电容在承受平行于内电极方向或垂直于内电极方向的压力时其容值随施加压力的变化。
4 单轴静压条件下高压陶瓷电容的容值变化
通过万能材料试验机,分别从平行于内电极的方向、垂直于内电极的方向对样品表面施加约10 MPa、20 MPa、40 MPa、60 MPa、80 MPa、100 MPa、120 MPa的静压,压力增加至电容破坏。
4.1 施加压力平行于内电极方向
当施加的压力平行于内电极方向时,电容承受应力与电容容值随时间的变化如图9所示。
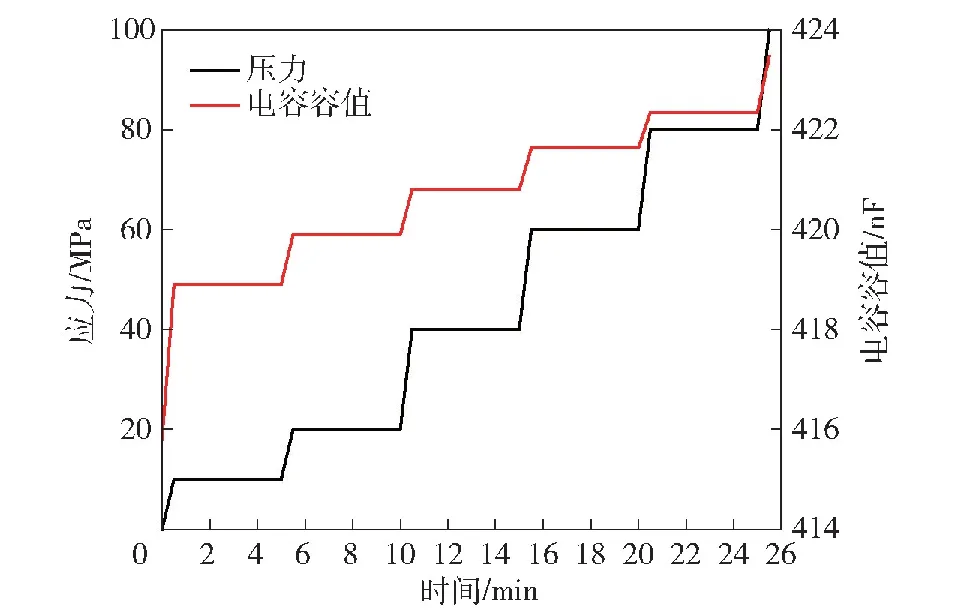
图9 电容承受应力与电容容值随时间变化Fig.9 Variations of stress and capacitance with pressure
3块高压陶瓷电容样品的电容容值随施加压力的变化如图10所示。
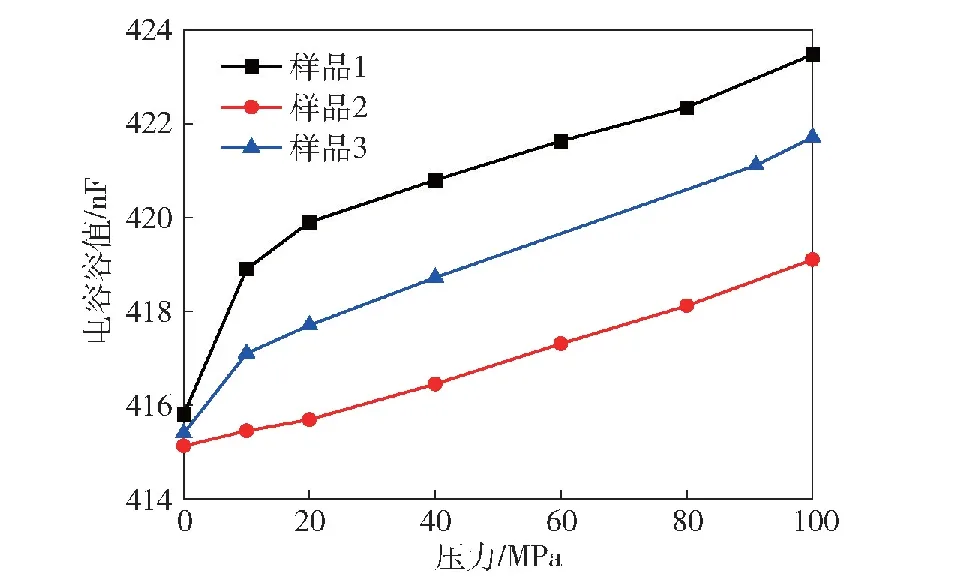
图10 压力平行于内电极方向时电容容值随压力变化Fig.10 Variation of capacitance with pressure parallel to the direction of inner electrode
由图10可知,当施加的压力平行于内电极方向时,高压陶瓷电容容值随施加压力的变大而变大,容值变化幅度分别约为5.08 μF/100 MPa、5.12 μF/100 MPa、4.67 μF/100 MPa。则对于该高压陶瓷电容样品,当受到平行于内电极方向的压力时,容值将增大,幅度约为1.2%/100 MPa。
4.2 施加压力垂直于内电极方向
当施加的压力垂直于内电极方向时,电容承受压力与电容容值随时间的变化如图11所示。

图11 电容承受压力与容值随时间变化Fig.11 Variations of stress and capacitance with pressure
3块高压陶瓷电容样品容值随施加压力的变化如图12所示。
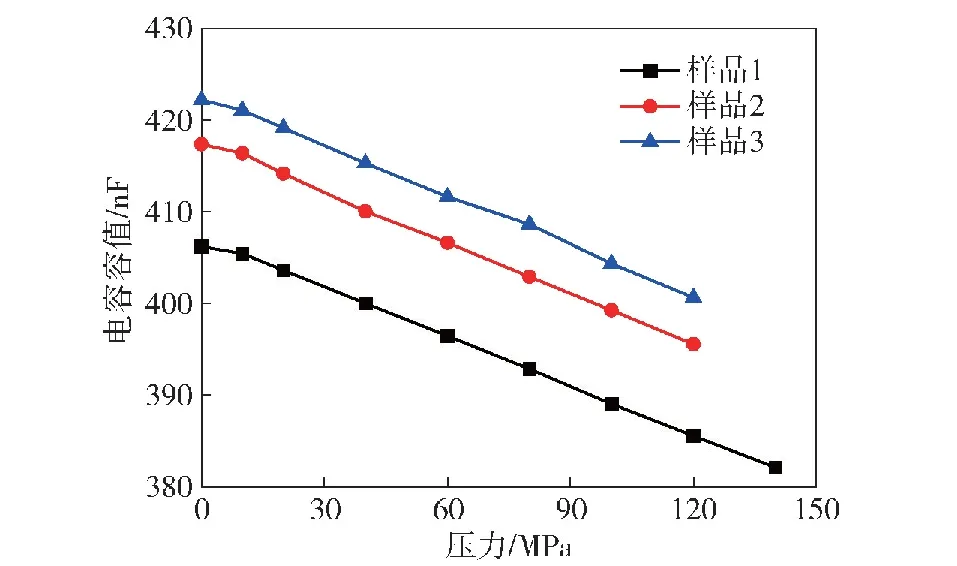
图12 压力垂直于内电极方向时容值随压力变化Fig.12 Variation of capacitance with pressure perpendicular to the direction of inner electrode
由图12可知,当施加的压力垂直于内电极方向时,高压陶瓷电容容值随施加压力的变大而减小,容值变化幅度分别约为-17.21 μF/100 MPa、-18.16 μF/100 MPa、-17.96 μF/100 MPa。则对于该高压陶瓷电容样品,当受到垂直于内电极方向的压力时,容值将减小,幅度约为-4.3%/100 MPa。
5 结果分析与讨论
在静压条件下,高压陶瓷电容的内电极、介质材料应力状态应是均匀的。利用ANSYS WORKBENCH软件建立简化的高压陶瓷电容有限元模型,模型中陶瓷体、内电极与介质材料的材料参数如表1所示,有限元模型如图13所示,其中陶瓷体与介质材料为BaTiO3,内电极材料为Ni。因内电极厚度很薄,采用壳单元模拟内电极结构,实体单元模拟介质材料。通过该模型,分析高压陶瓷电容在平行于内电极方向与垂直于内电极方向、幅值为 100 MPa的压力作用下内部介质材料的应力状态。

图13 简化高压电容局部几何模型Fig.13 Simplified geometric model of the high-voltage capacitor
5.1 施加压力平行于内电极方向时
对高压陶瓷电容平行于内电极方向的表面施加100 MPa的压力时,介质材料沿极化方向的应力状态如图14(即图2中的3轴方向)所示。

图14 电容在平行于内电极方向压力作用下的应力分布Fig.14 Stress distribution of capacitor under pressure parallel to the inner electrode
从图14中可以看出,在100 MPa、平行于内电极方向的压力作用下,内部介质沿极化方向的应力状态以张应力为主,约为2.3 MPa。结合静压试验结果,电容受到平行于内电极方向的100 MPa压力时,即内部介质材料沿极化方向的应力为2.3 MPa,容值增大1.2%。
5.2 施加压力垂直于内电极方向时
对高压陶瓷电容垂直于内电极方向的表面施加100 MPa压力时,介质材料沿极化方向的应力状态如图15(即图2中的1轴方向)所示。
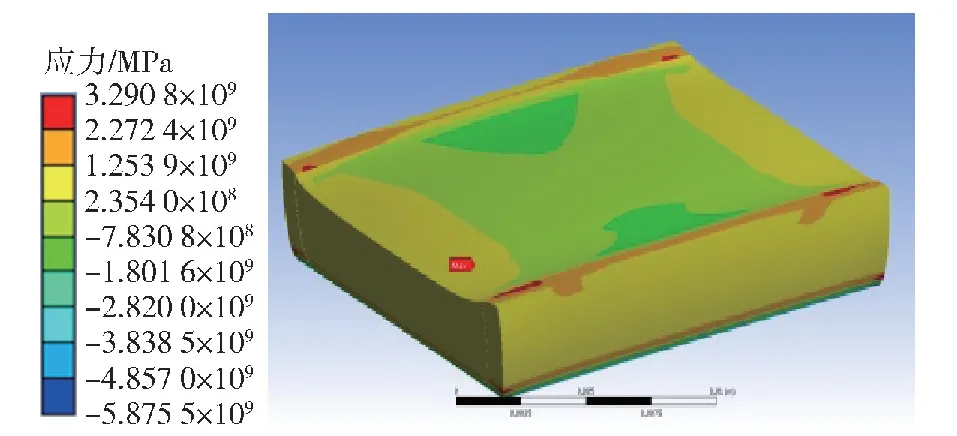
图15 电容在垂直于内电极方向压力作用下的应力分布Fig.15 Stress distribution of capacitor under pressure perpendicular to the inner electrode
从图15中可以看出,在100 MPa的垂直于内电极方向的压力作用下,内部介质材料沿极化方向的应力以收缩压应力为主,约为-81.4 MPa。结合静压试验结果,电容受到垂直于内电极方向的100 MPa压力时,即内部介质材料沿极化方向的应力为-81.4 MPa,容值减小4.3%。
5.3 试验与计算结果对比
基于建立的有限元模型,计算高压陶瓷电容在平行于内电极方向与垂直于内电极方向,大小为10 MPa、20 MPa、40 MPa、60 MPa、80 MPa、100 MPa、120 MPa的压力作用下,内部介质材料沿极化方向的应力状态(平行于内电极方向的作用力提取沿电容厚度方向的应力分量,垂直于内电极方向的作用力提取沿电容宽度方向的应力分量),如表4所示。
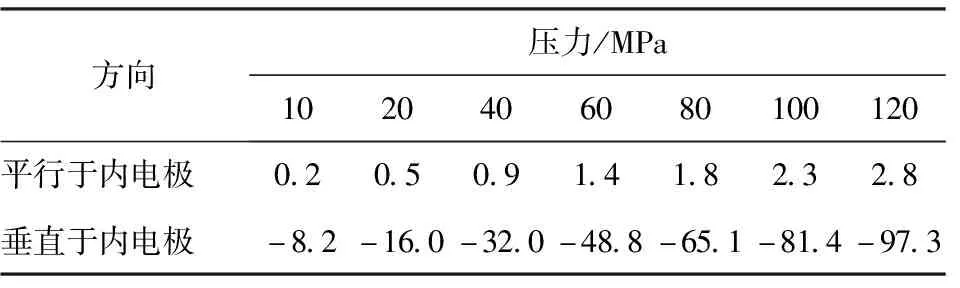
表4 不同幅值的压力作用下介质材料的应力状态Table 4 Stress state of the dielectric material under pressure of different amplitudes MPa
从表4中可以看出,内部介质材料沿极化方向的应力峰值与外部施加应力基本成线性关系。结合唯象热力学理论模型,通过式(4)、式(5)、式(6)计算得到内部电场强度为25 MV/m时,在0.2 MPa、0.5 MPa、0.9 MPa、1.4 MPa、1.8 MPa、2.3 MPa应力作用下介质材料的介电常数。对比在平行于内电极方向压力作用下的材料介电常数变化率与电容容值变化率,如图16所示;同样地,通过式(4)、式(5)、式(6)计算得到内部电场强度为25 MV/m时,在-8.2 MPa、-16.9 MPa、-32.5 MPa、-48.8 MPa、-65.1 MPa、-81.4 MPa、-97.3 MPa应力作用下介质材料的介电常数。对比在垂直于内电极方向压力作用下的材料介电常数变化率与电容容值变化率,如图17所示。
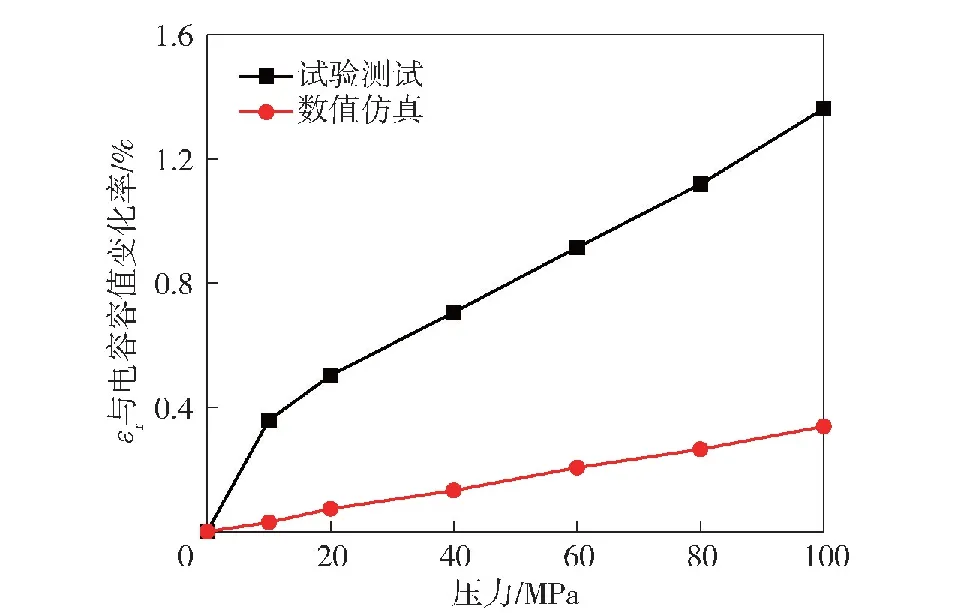
图16 平行于内电极方向的压力作用下材料介电常数变化率计算结果与高压陶瓷电容容值变化率测试结果对比Fig.16 Comparison of simulation results and test results of the change rate of dielectric constant of the material under pressure parallel to the inner electrode

图17 垂直于内电极方向的压力作用下材料介电常数变化率计算结果与高压陶瓷电容容值变化率测试结果对比Fig.17 Comparison of simulation results and test results of the change rate of dielectric constant of the material under pressure perpendicular to the inner electrode
如图16和图17所示:综合唯象热力学理论模型计算结果与高压陶瓷电容静压试验结果,可以知道平行于内电极方向的压力将在介质材料内部产生张应力,材料介电常数变大,高压陶瓷电容容值升高;垂直于内电极方向的压力将在介质材料内部产生压应力,材料介电常数减小,高压陶瓷电容容值降低。
从变化趋势来看,唯象热力学理论模拟结果和静压试验结果十分吻合。然而计算结果和测试结果在数值上之间仍然存在一定差别,产生这一差别的原因主要有两点:1)在唯象热力学理论模型中忽略了掺杂组元对体系自由能的影响;2)高压陶瓷电容在高温烧结过程中将产生残余应力,唯象热力学理论模型忽略了材料内部残余应力的影响。
6 结论
本文为分析外部力场对带电高压陶瓷电容的容值等关键性能的影响,采用唯象热力学理论模型对外力作用下介质材料的介电性能变化进行了分析。得出以下主要结论:
1) 内部压应力引起材料介电常数减小,内部张应力引起材料介电常数增大。
2) 模型计算结果、高压陶瓷电容静压试验结果与高压陶瓷电容简化有限元分析结果表明,平行于内电极方向的压力在介质材料内部产生张应力,推动铁电畴壁的运动引起材料介电常数增大,导致高压陶瓷电容容值升高。
3) 垂直于内电极方向的压力在介质材料内部产生压应力,增强电场对于铁电畴壁的夹持作用,引起材料介电常数减小,导致高压陶瓷电容容值降低。

