基于Matlab/Simulink燃料电池系统数字孪生模型开发

张依民　梁满志

摘 要：文章主要用了Matlab/Simulink软件对PEM燃料电池系统进行数字孪生模型开发，并且采用半机理半经验的模型搭建方法，将PEM燃料电池系统中的重要辅助子系统：电堆、空气供给系统与冷却系统等模型的搭建过程详尽的讲解。

关键词：PEM燃料电池系统 数字孪生模型 电堆模型 空气子系统模型 冷却系统模型 系统建模

The Development of Digital Twin Based on the Matlab/Simulink Fuel Cell System

Zhang Yimin Liang Manzhi

Abstract：This paper mainly uses Matlab/Simulink software to develop a digital twin model of PEM fuel cell system， and adopts the semi-mechanism and semi-empirical model construction method to explain in detail the construction process of the important auxiliary subsystems of the PEM fuel cell system： stack， air supply system and cooling system.

Key words：PEM fuel cell system， digital twin modelm， stack model， air subsystem model， cooling system model， system modeling

1 引言

PEM燃料电池具有许多可圈可点的优点，例如：运行时电池温度低、能效高、启动快、无污染，但是对中型和大型的燃料电池系统来说，它们的内部组成、系统的内部结构和所需的运行条件也都还较为复杂，这样使其维修拆卸与故障寻找相对困难，所以对于PEM燃料电池还有着非常大的发展前景。那么想要实现对PEM燃料电池系统的优化控制、实时的可视化监控、故障诊断以及综合管理，就不得不提到近年来在各个领域大方光彩的数字孪生技术。

数字孪生是充分利用物理模型、传感器更新、运行历史等数据，集成多学科、多物理量、多尺度、多概率的仿真过程，在虚拟空间中完成映射，从而反映相对应的实体装备的全生命周期过程[1]。通俗来说就是：数字孪生就是在一台设备上或者一个系统的基础上，创建一个与现实对象一样的数字版的对象，这样现实对象与数字世界对象就好比为亲生的“孪生兄弟”一样，并且他们一模一样并且实时同步，甚至数字世界里面的对象比现实中的对象可以更快的预测未来发生什么并提前告诉你将要怎么样去应对。所以数字孪生连接起了物理与信息数字世界，并且它有着可视化、高校分析、数据实时跟踪以及预测未来的众多应用价值。本文就是采用半机理半经验的方法对PEM燃料电池系统进行详细数字孪生模型开发建模。

2 电堆的模型建立

2.1 电堆电压模型建模

燃料电池系统的核心是电堆，而电堆的核心是电压。所以结合燃料电池电堆的欧姆极性损失、浓差极化损失、活化极性损失，并且根据现在已有的PEMFC输出特性经验公式，可以获得燃料电池单个的输出电压：

（1-1）

式中，—能斯特开路电压，可以用下列公式表示：

（1-2）

式中，为燃料电池温度（K）；为氢气分压和氧气分压。

能斯特开路电压模型模型搭建方法正如上面1.1中的（1-2）公式表達

欧姆极化损失是因为电解质中的质子与导电元件中电子的阻抗而诱发的，其公式可表达为：

（1-3）

式中，为内部电阻，单位为为质子交换膜的厚度；为传导率；为质子交换膜含水量；，为经验常数分别为：0.005139、0.00326、1268。

浓差损失是由于燃料在发生反应时消耗导致了浓度发生了变化而产生的。这些损耗也是高电流密度下电压下降迅速的原因。

浓差极化损失电压（）表达如下：

（1-4）

式中，B为经验常数；是燃料电池运作时电流密度最大值（mA/cm2）；为燃料电池运作时的电流密度（mA/cm2），参数是导致电压急剧下降时的电流密度。

活化极性损失是克服催化表面上电化学反应所需的活化能而产生的过电势，它在低电流密度的电损失里起到了主导作用，可由Butler-Volmer方程推导得到[2]：

（1-5）

式中，其中为电流密度为零时的压力损失，和为常数。活化极性损失与电堆温度及氧气分压有关。

将上述所以电压损失集合起来，所以电池工作电压表示为：

（1-6）

而电堆通常时由多个或几十个电池串联而成，为此燃料电池电堆电压表示为：

（1-7）

根据（1-6）（1-7）公式以及上述的模型，可以搭建出电堆电压模型。

2.2 阴极流量建模

阴极模型可以描述出燃料电池电堆阴极内部的气体流动特性，本文基于文献[3]中的模型基础利用质量守恒原理和空气的热力学特性来建立相关模型，并且做出下列几条合理的假设：该模型中所以的气体都认为时理想气体；流道内的温度等于电堆温度，且温度由冷却系统来控制，使其温度维持在80℃左右；阴极流出的流量变量，即压力、湿度、温度等与流入相同；忽略空间阴极内空间变化[6]。

2.2.1 质量流量模型

根据氧、氮和水的质量流动的连续性，建立了三种状态方程，即：

（1-8）

（1-9）

（1-10）

由于阴极气体的饱和状态，所以阴极内的水可以为液体与蒸汽两种状态存在。因此气体所能容纳的最大蒸汽质量，可以由蒸汽饱和压力计算出来，即：

（1-11）

如果公式（1-10）中计算的水的质量大于饱和状态的质量，则多出的蒸汽会瞬间凝结成液体。为此不难得出：

（1-12）

2.2.2 压力模型

阴极内腔中各气体压力关系为：

式中，分别是氧气、氮气、蒸气分压。

2.2.3 电化学反应模型

燃料电池工作时，气体不断地进入发生化学反应，其中反应消耗的氧气质量流量以及生成水的质量流量为：

（1-13）

2.2.4 入口质量流量特性模型

（1-14）

上述公式可以计算入口蒸汽压，其中为相对湿度、为饱和压力、为入口温度。

又因为潮湿空气是干燥空气和蒸汽混合而成，为此干燥空气分压就等于总压和蒸汽压之差：

（1-15）

相对湿度为：

（1-16）

空气的摩尔质量为：

（1-17）

干燥空气和蒸汽进入阴极的质量流量为：

（1-18）

氮气和氧气的质量流量为：

（1-19）

结合以上公式，即可得到入口质量流量特性模型。

2.2.5 出口質量流量特性模型

在已知阴极出口总流量的基础上，计算出口氧气、氮气和蒸汽的质量流量，计算方法与进口流量相似。最后得到出口质量流量特性模型。

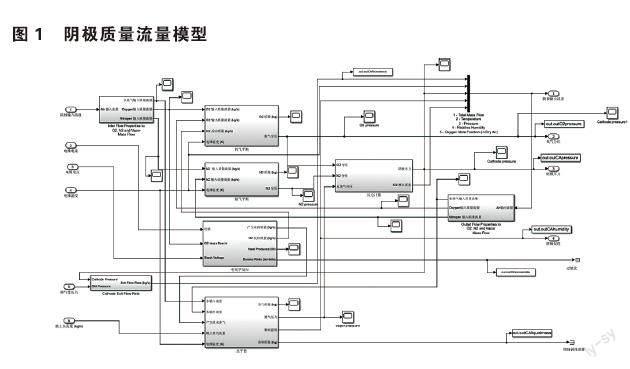
2.2.6 阴极质量流量模型

结合以上模型，就可得到阴极质量流量模型如图1所示：

2.3 阳极流量建模

与1.2阴极流动模型相同，氢分压和阳极流动湿度是通过平衡阳极中氢和水的质量流量来确定的。且阳极的气体只有氢气与蒸汽。所以就不多赘述过程，参考1.2就可以轻松得到阳极流量模型。

2.4 膜水含量模型

膜水含量模型表示膜中的含水量和水通过膜的质量流速。膜含水量和通过膜的质量流速是电堆电流和阳极、阴极流道内流体的相对湿度的函数。阴极和阳极流体的相对湿度分别是阴极质量流量模型和阳极质量流量模型的输出。本文是采用文献[3]的模型基础来进行详细搭建。

通过膜的水的总质量流量为：

（1-20）

膜水活度是阴阳两极中气体水活度的平均值为：

（1-21）

膜中的水含量由水活度计算为下：

（1-22）

而膜平均含水量在气体范围内等于相对湿度，为此电渗透阻力系数以及电渗透系数为：

（1-23）

最终得到膜渗透模型分段计算式如下：

（1-24）

由以上式子可以分别对质子交换膜上水流量、平均含水量、渗透模型分别进行建模。

2.5 电堆模型

集合1.1、1.2、1.3、1.4中的各个子模型，即可得到电堆仿真模型。

3 空气供给系统的模型建立

供给系统是对将要进入燃料电池的空气进行适当的过滤、加压、加湿，来保持燃料电池堆阴极侧的温度、压力、湿度及空气流量以达到氢氧反应与电池工作的适宜范围；而且空气供给系统中又包含了五个子模型，它们分别为空压机和单机模型、中间冷却器、进气管路模型、加湿器与回返管理模型。并且为了方便后续空气供给系统的模型建立与研究，进行下列假设：1）阴极管路内温度等于电堆温度且保持恒定；2）干燥空气是由78%的氮气与百分之21%的氧气组成。

3.1 空压机建模

空压机模型分为两部分进行研究，第一部分是静态空压机map，它确定了通过空压机的空气流速，然后用热力学方程来计算出口空气温度和所需的空压机功率[8]。第二部分表示空压机和电机的惯量，并定义空压机的转速。因此，在空压机map中使用速度来确定空气的质量流量。为此，采用非线性曲线拟合方法对空压机特性进行建模[8]。

因为压缩机性能会随着工作环境的变化而发生改变，根据文献[8]的方法对空压机转速和入口处空气流量进行了修正，修正关系为，，其中修正后的温度/288K，修正后的压力/1atm。空压机流量可用无量纲头参数修正：

（2-1）

为空压机叶轮直径（0.2268m），为气体比热容之比，在气体是空气的情况下为1.4。

（2-2）

其中为空气密度，又有：

（2-3）

其中，、、和是马赫数的多项式函数：

（2-4）

（2-5）

（2-6）

入口马赫数为：

（2-7）

其中是气体常数，所以可以得出空压机的空气流量为：

（2-8）

其中分别为：1.23（kg/m3）、0.2286（m）

计算空气离开时的温度如下：

（2-9）

由上可搭出空压机的模型。

3.2 管路模型

在供气管路体积是包括空压机与电堆之间的管路体积以及冷却器和加湿器的体积。返回管路是包括在电堆排气管道体积和背压阀的体积，本文采用文献[4]中的模型基础进行详细搭建模型。

根据质量守恒定律，对于任意管路，有：

（2-10）

其中，m为积聚在管路体积中的气体质量，和为流入和流出管路的质量流量。假设管路内温度T恒定，且等于入口气流温度T=，则管路内等温关系为：

（2-11）

其中是空气的气体常数，V是管路体积。如果管路中的空气温度发生了变化，则由能量守恒和理想气体定律可得的压力动态方程为：

（2-12）

以上述为基础，假设管路内空气温度是恒定的，则用公式（2-15）对管路进行建模；如果空气温度在管路内发生了变化，则使用公式（2-14）和公式（2-16）。

进气管路与返回管路的出口流量是由管路与容器的下游一起决定的，为此根据实际压比与临界压比得出流量表达式。

临界压比公式如下：

（2-13）

其中是气体比热容的比值，即；对于空气其值为=1.4，临界值为0.528；是内部气体压力；是容器下游气体压力。

流量与压力之间的表达式如下：

（2-14）

3.3 中冷器建模

本文中冷器模型为理想模型且参考文献[6]进行详细建模。设定中冷器保持空气进入电堆的温度在=80℃上下且内不存在压降，既气体离开中冷器的压强与进气管路压强相同，=。因为气体湿度会被温度影响，因此利用饱和压力方程：

（2-15）

来计算出离开中冷器的气体湿度：

（2-16）

式中，是为温度T相对应的饱和蒸汽压强，从而得到中冷器模型。

3.4 加湿器建模

中冷器的气体在进入电堆前，会通过向加湿器气流中注水的方式进行加湿。由于加湿器的体积较小，因此它可以被认为是供应管路体积的一部分[7]。由相对湿度公式为：，其中为混合气中蒸汽的分压，为混合气体温度下的饱和压力。

故可以得出蒸汽的压力为：，由于潮湿空气是干燥空气和蒸汽的混合物，因此干燥空气分压就是总压和蒸汽压之差：，湿度比为：，其中为干空气的摩尔质量（28.84×10-3kg/mol）。

从冷却器排出的干空气和蒸汽的质量流量为：

（2-17）

蒸汽流速和压力为：

（2-18）

由蒸汽压可以用来确定出口相对湿度：，由于蒸汽压增加，总壓也增加，总压为：，由质量连续性，加湿器出口流量为：

（2-19）

由以上公式，可得加湿器模型。

4 仿真结果对比并总结

将上述所以子系统模型进行集合并且仿真测试，其中燃料电池系统电压输出与功率、空压机转速与功率、阴极压力与输出流量、氧气分压与阴极湿度等仿真结果如图2所示。

综上对所建模型的各项数据与实际的燃料电池系统进行比对，总体上所建数字孪生模型准确率已经达到了93%左右，这已经很好的模拟了真实的燃料电池系统，这将对后续的真实燃料电池系统与燃料电池系统数字孪生模型相互融合与开发奠定了一定的基础与可用的参考价值。

参考文献：

[1]数字孪生模型在产品构型管理中应用探讨.航空制造技术．2017.

[2]AMPHLETT J C， BAUMERT R M， MANN R F， et al. Parametric modelling of the performance of a 5-kW proton-exchange membrane fuel cell stack[J]. Journal of Power Sources，1994，49（1/3）：349-356.

[3]王婷. 燃料电池汽车整车散热系统仿真模拟和实验研究.华中科技大学.动力工程.

[4]宋天助. 燃料电池动力系统特性及其控制研究[D].吉林大学，2019.

[5]Xiao， Fangzhu， Huang， Tao， et al. Optimization analysis and mechanism exploration on the removal of cesium and the solidification of secondary residue wastes in electrokinetics [D]. February 2019 Environmental Progress & Sustainable Energy 38（5） DOI：10.1002/ep.13181.

[6]于潇. 氢燃料电池系统建模与气体供给系统控制方法研究[D].吉林大学，2022.DOI：10.27162/d.cnki.gjlin.2022.005461.

[7]徐彩前. 质子交换膜燃料电池建模与湿度优化控制[D].电子科技大学，2022.DOI：10.27005/d.cnki.gdzku.2022.004995.

[8]王昭懿. 车用质子交换膜燃料电池空气供给系统建模及控制策略研究[D].吉林大学，2022.DOI：10.27162/d.cnki.gjlin.2022.005159.

[9]吕雪. 氢燃料电池发动机冷却系统建模分析及控制策略研究[D].太原理工大学，2021.DOI：10.27352/d.cnki.gylgu.2021.001620.