面向机械方向学科融合的数值分析课程教学改革与实践

胡永旭

摘 要：数值分析课程是高等院校机械类专业的公共类课程或专业选修类课程，提高数值分析课程教学质量有助于帮助学生获取利用数值计算方法解决工程实际问题的能力。针对数值分析课程与机械类专业课程融合不足的问题进行了探讨，论述了以解决机械学科专业问题为导向，以数学软件为工具，以机械学科专业知识融合为教学目的的数值分析课程教学改革的多项举措。以理论力学和汽车试验技术为例讲解了面向机械专业的数值分析课程教学改革方法，以支持向量机的求解问题讲解了数值分析课程如何与学科前沿理论知识结合。最后倡导了以学科融合为主，通过动画展示和引入学科前沿知识激发学生学习数值分析兴趣的教学理念。

关键词：数值分析 学科融合 教学改革 动画教学

Teaching reform and practice of numerical analysis course for integration of mechanical disciplines

Hu Yongxu

Abstract：The course of numerical analysis is a public course or a professional elective course of engineering subject in colleges and universities， improving the teaching quality of numerical analysis course is helpful to help students acquire the ability to solve practical engineering problems by using numerical calculation method. This paper discusses the integration of numerical analysis course and other professional courses， and discusses several measures of numerical analysis course teaching reform which is oriented to solve the professional problems of related disciplines， takes mathematical software as the tool， and takes disciplinary integration as the purpose of teaching. Taking theoretical mechanics and automobile test technology as examples， the teaching reform method of numerical analysis course for mechanical specialty was explained， the purpose of introducing frontier theory knowledge is explained by solving the problem of support vector machine. Finally， it advocates the teaching concept of integrating disciplines， stimulating students' interest in learning numerical analysis through animation display and introducing frontier knowledge of disciplines.

Key words：Numerical analysis; Integration of disciplines; Teaching reform; Teaching of animation

1 引言

數值分析课程是高等院校机械专业的公共类课程或专业选修类课程，该课程着重于锻炼学生将复杂非线性数学问题转换为简单线性数学问题的能力，并要求学生能够利用迭代或近似方法对问题进行求解。同时，数值分析课程也是培养学生实践能力的一门课程，完成数值分析课程的学习后，学生应当能够用数学语言描述机械专业的复杂问题，并且能够构造数值计算算法和利用计算机软件进行问题的求解。但传统数值分析课程的教学一般仅针对数值求解问题本身，而未与机械专业中的其他课程产生联系，导致学生无法使用数值分析工具解决机械专业的实际工程问题。将各专业学科进行交叉融合，使大学教育形成一个有机整体一直是教育者们关注的问题，各研究者也提出了很多相关的教育理念[1，2]，但数值分析课程与机械学科专业知识的学科融合教学改革研究稍显不足。

2 数值分析课程的特点及教学中的不足

数值分析课程主要包含了插值计算，拟合分析，数值积分与微分，非线性与线性方程组求解，常微分方程初值问题的数值解法等内容，其特点是：（1）公式推导较多，推导过程较复杂且需要一定抽象思维；（2）算法构建基于近似和等效，将非线性复杂问题转化为了线性问题；（3）算法便于在计算机上编程实现。这些特点决定了数值分析是一门知识丰富、理论抽象、实践性非常强的课程。

但是从现状来看，数值分析课程教学存在以下方面的问题：（1）教学内容仍偏重于理论。受到课时数的限制，数值分析课程一般都将教学重点放在数值计算的理论讲解方面，应用数值分析理论进行建模和求解的实践教学课时较少，其结果是学生仅仅初步了解了数值计算的理论原理，但没有通过深入实践学会如何提出问题和解决问题。2）理论教学没有和机械专业其他课程的理论知识融合，无法形成学科体系。对于机械专业学生来说，数值计算算法是解决本学科专业问题的有利工具，数值计算方法和专业中的其他理论问题存在着天然联系，但是目前针对数值计算的教学没有能够将机械专业课程的理论知识融入到教学内容中，使得数值分析课程的教学内容空洞且没有着力点。3）实践课题与现实工程问题联系不紧密，探讨问题过于数学模型化。数值分析针对的问题是实际工程中所面对的问题，但是目前课程教学实践的内容仍是基于一般数学问题（方程，方程组，微分方程，积分求解等），没有将实际工程问题与数值求解方法结合起来，导致实践内容无法激起学生学习的兴趣，实践效果较差。

对于数值分析课程目前存在的一些问题和不足，许多教育工作者提出了解决方法并进行了方法实践，如以数学建模为实践内容进行数值分析课程教学改革，加强理论教学与实践教学的联系，或在教学过程中加入数学史的介绍，让学生了解学科的发展过程等[3-6]。

3 以学科融合问题为导向构筑理论教学内容

从数值分析课程的特点来看，拟合分析与机械材料的疲劳曲线解析表達存在一定联系，常微分方程数值问题与机械专业的力学相关课程和专业知识联系较紧密，其他章节课程也都和学科中其他课程的专业理论知识存在一定关联，因此可以以学科融合问题为导向构筑理论教学内容。

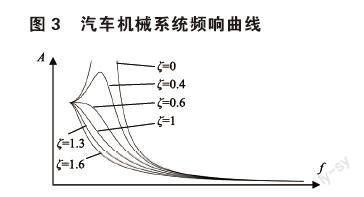
以汽车外形设计为例，如图1所示，当汽车外形的关键点的尺寸[（x1，y1），…， （x1，y1）]确定后，其余位置的汽车外形轮廓点坐标可以用三次样条插值方法进行计算，得到的设计轮廓具有过渡平滑，流线型强的特点，可以辅助工程师进行汽车轮廓设计。此外，拟合方法可以帮助学生以函数形式理解主尺寸选用的原则；非线性方程组求解方法可应用于优化问题；微分方程的初值问题可以用于求解理论力学中的动力学问题等。

学科融合的根本目的在于加强学生对机械专业知识的理解，起到温故而知新的作用，同时为后续课程的学习提供平台。由于学科融合的本质是锻炼大学生的知识综合运用能力，因此学科融合后的教学内容既有利于学生对数值分析知识的理解，又有利于机械专业的学生加强对专业理论知识的掌握，非常全面，起到了综合训练的作用。大学生的专业课程和未来的工作内容有着紧密联系，具有很强的现实意义，因此面向多学科融合的数值分析课程能够帮助学生在未来更好解决实际工作问题。将数值分析教学内容与机械专业的其他理论紧密结合也为学生的仿真分析学习提供了有力的平台，实现了教学和科研的良性互动，促进了教学和实践的联系。

4 将求解过程用动画展示，帮助学生理解，提高学生兴趣

以往数值分析计算的求解结果都是以曲线或图表进行展示，该种方法有利于学生理解结果和算法之间的内在联系，却不利于提高学生对工程问题解决方案的感性认识。例如多连杆机构的尺寸设计是机械专业理论力学课程的基本教学内容，专业课主要是教学生如何使用解析方法求解各连杆的尺寸，但是由于缺少动画展示，学生对确定尺寸后的多连杆机构运动特性没有感性认识。

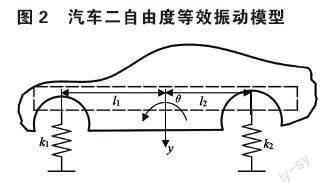
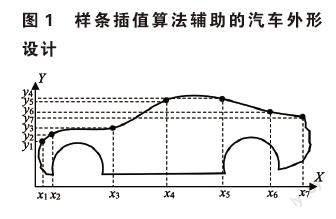
在汽车试验技术这门课中，教材用车身动力学频响曲线（如图3所示）解释车身的共振区间以及不同频率激励力下的车身振动特征，但是学生无法通过教材真实感受到不同频率激励力作用下汽车的振动位移，教学效果较差。如图2所示，汽车的垂向振动特性和俯仰振动特性可以用弹簧-质量等效动力学模型进行描述，描述微分方程为式（1）。

式中：k1为前悬架刚度，k2为后悬架刚度，M为车身质量，J为车身俯仰转动惯量，l1为前悬挂到汽车车身质心的距离，l2为后悬挂到汽车车身质心的距离，z为车身垂直运动距离，θ为车身俯仰角度，Fz为是的车身发生垂向运动的作用力，Mθ为使车身发生俯仰运动的作用力矩。在给定输入条件下，微分方程（1）可以应用数值计算中的欧拉法，梯形公式，龙格库塔法等算法求解。在使用数值方法进行求解时，输入激励力和力矩的频率可以设置为如式（2）所示的连续变化，这样既可以帮助学生理解用扫频法获取系统函数的原理，又可以通过动画演示不同激励频率下车身的振动幅度让学生对汽车的共振有更深刻的理解。

现在很多的数学软件（MATLAB， Maple等）都具有制作动画的功能，借助动画缩放功能，学生能够直观感受地到车身的微幅振动的变化，更有利于学生理解频响曲线与实际车身振动的联系。除了能更好地帮助学生理解机械专业的知识以外，制作动画的过程还极大地锻炼了学生的编程能力。动画制作训练了学生的程序规划，函数调用，程序调试等技能，对于学生掌握计算机编程语言，学会用计算机程序实现数值分析算法十分有益。

5 引入学科前沿理论知识，深化学科认识

课程教学内容的更新和改革已成为大学教学改革的一项重要内容，但总体上看数值分析课程教学内容的更新速度滞后于机械学科前沿成果的发展速度，没有将最新的机械学科理论知识与数值算法紧密结合起来。目前数值分析算法已经成为机械领域设计、材料、故障诊断等问题求解的必要手段，如有限元分析，动力学分析，人工智能的计算问题都与数值算法息息相关。例如在人工智能领域，支持向量机技术已经成为解决分类决策问题的一种重要方法，支持向量机的数学公式表述可以是不等式条件下的条件极值问题，即：

式中：γ为样本点到分类超平面的距离，y为样本的决策属性值，为±1，w为分类超平面的系数，是一个n维的向量，b是分类超平面的参数标量。引入拉格朗日乘数后，式（3）的函数表达式为：

对于仅含等式约束的条件极值问题，可以直接由式（4）对各变量求偏导数获得问题的解，但是对于含有不等式约束的条件极值问题，则必须用KKT条件将条件极值问题转化为无条件极值问题再进行求解。引入KKT条件后，式（4）的求解方程为：

关于式（5）的求解，当问题的维度较低或样本数量较少时，可以用牛顿迭代法，但是当样本较多或维度较高时，需要将式（4）化为对偶问题，再利用KKT条件求解。化为对偶问题后，式（4）的求解方程为：

目前数值分析课程中的求解方法已经不能满足式（6）的快速求解，而必须使用启发式（SMO）算法进行求解。启发式 算法由微软研究院提出，是目前运行速度最快的二次规划优化算法，特别适合线性支持向量机模型的学习或数据稀疏场景。教师通过讲解支持向量机问题可以引入新的数值求解方法，通过对新的数值求解方法的讲解有利于为学生拓宽数值计算和计算机方面的知识，深化对人工智能的理解和认识。

通过将机械专业前言理论知识与数值分析课程教学内容进行融合可以极大地拓宽学生的科学视野，有利于培养学生的创新意识，更有助于学生未来的发展。因此，教师可以基于自己的学术研究领域，在教学中通过实例讲解适当地将一些新的机械专业成果和实践经验贯彻到课堂教学和实践中，这既保证了教学内容与学科前沿的紧密结合性，又提高了学生的学习兴趣。

6 结语

作为数学理论和计算机科学结合的产物，数值分析算法和学科专业知识存在着紧密的联系。针对目前数值分析课程存在的与机械专业知识联系不紧密，结果展示方法单一，教学内容滞后于机械学科前沿理论的问题进行教学改革是必要的。面向多学科融合的数值分析课程教学改革与实践的目的是增强数值分析课程与机械专业课程的联系，借助数值计算课程将机械专业大学课程形成统一的整体，达到优化教学过程，提升教学质量，实现教师与学生良好互动的目的。

参考文献：

[1]魏朋，杨红英，张一风，等. 多学科交叉融合工程人才培养模式探索与实践——以非织造材料与工程专业为例[J]. 高分子通报，2022（3）：7.

[2]张戎，刘新建，许宁，等. 多学科协同教学的应用初探——以“人兽共患病学”教学为例[J]. 教育教学论坛，2022（30）：5.

[3]刘艳伟，司军辉. 数值分析课程教学改革若干问题探讨[J]. 黑龙江教育学院学报，2010（6）：2.

[4]沈海龙，邵新慧，宋叔尼. 数值分析课程教学改革的探索与实践[J]. 大学数学，2013（5）：1-3.

[5]袁海燕，宋成.应用型人才培养模式下《数值分析》教学改革的几点探讨[J]. 学理论，2012（3）：2.

[6]覃桂茳，涂井先，许成章，等. 翻转课堂教学模式在数值分析课程教学改革中的研究与实践[J]. 黑龙江科学，2022（009）：013.