磁悬浮流体机械喘振控制研究
关旭东 周瑾 金超武 徐园平 唐茂 崔恒斌
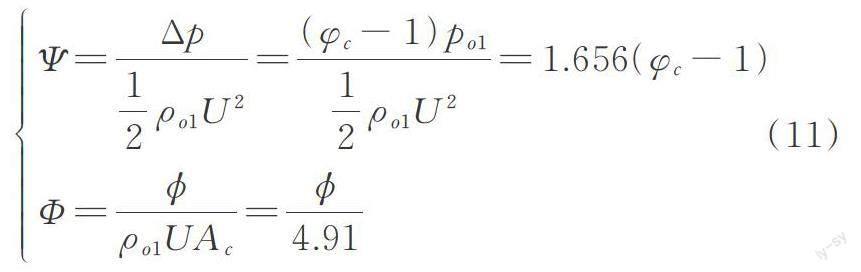
摘要 针对磁悬浮流体机械喘振问题,依据流体机械系统喘振状态时质量流量和压升的波动,采用基于质量流量的喘振控制策略。具体来说,利用喘振控制器求出叶轮轴向调节间隙值,并作为悬浮位置参考信号输入至轴向磁悬浮轴承闭环控制系统中,从而在轴向磁悬浮轴承系统作动下改变磁悬浮流体机械转子轴向位置,即改变叶轮叶尖间隙,以实现喘振的主动控制。仿真结果表明,当施加喘振控制时,可以扩展流体机械的稳定运行范围,由未控制下的15.5%节流阀开度扩展至喘振控制下的14%。通过模拟激振的方式辨识了喘振频率,并研究了PID控制器中控制参数对喘振控制性能的影响规律。
关键词 喘振控制; 磁悬浮流体机械; 磁悬浮轴承; 质量流量
引 言
当流量减少至临界稳定状态时,透平式流体机械会发生一种低频、大幅度的振动,该现象称为喘振[1]。磁悬浮流体机械也会发生喘振,能在极短的时间内损害流体机械,严重危害设备的正常运行。目前,针对喘振的解决办法大体包括喘振避免[2]和喘振控制[3]。前者的优点为结构相对简单、成本较低且运行可靠,但其縮小了流体机械的工作区域,牺牲了流体机械性能。后者则可规避前者的缺点,通过控制手段对喘振导致的流体波动予以补偿,稳定流体机械系统的流场状态,但执行机构响应时间一般较长。
实施喘振控制前需要对流体机械系统进行建模研究,可为喘振的机理及喘振控制提供前提。Badmus等[4]将流体机械系统的数学模型分成两类:一维模型与二维模型。前者可适用于预测流体机械喘振,后者则适用于流体机械的喘振与失速。通常,流体机械喘振失稳的数学模型采用第一种形式,而失速则一般发生在轴流式流体机械中,故多采用第二种形式。Emmons等[5]采用一维线性化模型研究压缩机系统稳定性,类比亥姆霍兹共振器,从而得到喘振的初始状态。Greitzer[6]针对轴流式压缩机系统采用非线性的集总参数模型,随后,Hansen等[7]将该模型应用至离心式压缩机中。Gravdahl等[1]在Greitzer模型的基础上,通过归一化避免了将额外的非线性引入系统,且模型方程平衡了转轴上的扭矩。针对二维模型,Moore等[8]研究了轴流式压缩机中不可压缩流动状态的旋转失速。随后,Ishii等[9]与Feulner等[10]将该二维模型用于可压缩流动状态。杜毅等[11]提出以电机转速和管道出口压力分别作为控制量和控制对象的风机管道模型,相比于原Greitzer模型,改进模型在计算管道出口压力时更精确。由于Greitzer模型具有结构简单及模型阶次低的优点,因此,其在喘振控制中的应用较为普遍,包括线性[12]与非线性控制[13]。Senoo等[14?15]改变离心式压缩机叶轮叶尖和蜗壳之间的间隙,研究其对压缩机性能的影响,在此基础上,文献[16?17]将Greitzer模型应用于磁悬浮压缩机中,并建立了调节管道压力的线性化模型。Yoon等[18]利用实验测试数据验证了磁悬浮压缩机系统数学模型,并通过实验辨识得到压缩机系统模型中的参数。Yoon等[19]将压缩机管道模型引入原始Greitzer方程,分析了压缩机压升对叶轮轴向间隙扰动的响应。
在传统流体机械的喘振控制中,通常采用的防喘振方法为固定与可变极限流量法[20]。通常,前者会降低流体机械的效率,而后者相对复杂且稳定性差。
Spakovsky等[21]和Wang等[22]以主动磁悬浮轴承(Active Magnetic Bearing, AMB)作为作动器,通过调整轴流式压缩机径向叶轮叶尖间隙对失速进行控制。Sanadgol等[23]指出磁悬浮压缩机中的喘振控制是利用轴向AMB系统调节叶轮的间隙来实现的,采用的物理机制是压缩机特性对叶轮叶尖间隙的敏感性,控制器的设计目标是系统运行轨迹保持在压缩机特性曲线上,从而确保叶轮的零稳态偏移并保持压缩机的效率,但其研究只限于仿真分析。基于磁悬浮压缩机试验台[24],Yoon等[25]采用轴向AMB调节叶轮叶尖间隙验证了喘振控制的有效性。Yoon等[26]基于具有可变叶轮叶尖间隙和管道声学特性的增强型压缩机系统模型,设计了磁悬浮压缩机喘振控制器,该喘振控制方法基于压缩机实验装置推导并实现,实验测试结果表明所提出的方法能够在不稳定的喘振区域运行时使压缩机系统稳定,从而将稳定流量范围扩大了21%以上。在磁悬浮流体机械喘振控制中,研究者还比较了多种流量估算方法对喘振控制的影响效果,结果表明控制器和流量观测器的最佳组合能够更大地扩展压缩机的运行范围[27]。此外,针对磁悬浮流体机械喘振控制器的设计,研究者分别成功运用了反步控制[28]、滑模控制[29]、分数阶控制[30]与H∞鲁棒控制[31]等方法。唐茂等[32]针对磁悬浮压缩机的喘振问题,分别采用了基于质量流量与输出压力的控制方法,仿真表明所采用的方法能够有效扩大压缩机的稳定运行范围。在此基础上,Guan等[33]将磁悬浮压缩机模型与磁悬浮轴承转子试验台进行联合,以获得半实物模拟喘振控制平台,分别验证了不同转速和参考调节轨迹下的模拟喘振控制效果。Ma等[34]考虑AMB控制系统的不确定性,针对轴向磁悬浮轴承转子系统设计了μ综合鲁棒控制器以抑制喘振引起的振动,并提出变平衡位置点的喘振控制策略,通过手动调节轴向平衡位置获得了抑制喘振的效果。
本文针对磁悬浮流体机械喘振问题,采用质量流量喘振控制策略,并基于PID控制器进行了磁悬浮流体机械喘振控制仿真。
1 流体机械系统Greitzer模型
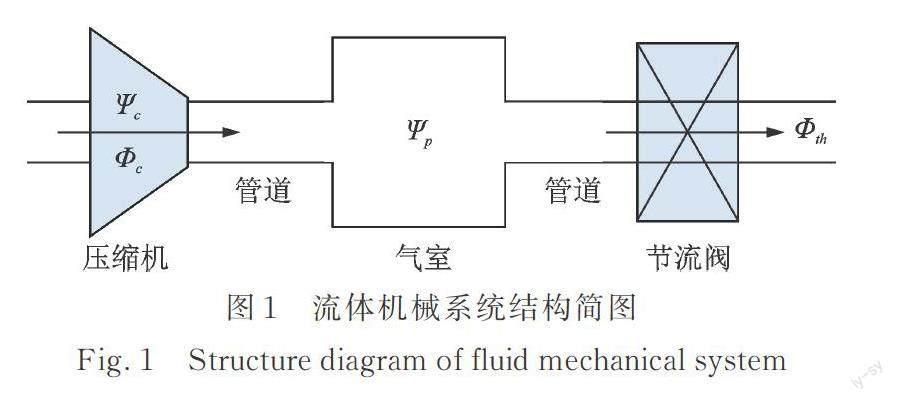
采用方程阶次相对较低、结构简单的Greitzer模型,在此基础上,引入磁悬浮轴承系统以进行喘振控制研究。以离心式压缩机系统为例,图1为流体机械系统简图,包括压缩机、管道、气室与节流阀。
图1中的符号均为无量纲,Ψ和Φ分别代表无量纲压升和质量流量;下标“c”,“p”和“th”分别代表压缩机、气室和节流阀。无量纲压升与质量流量分别表示为:
式中 ?p=pc-po1为压强增量(pc与po1分别为压缩机出口压强和进口大气压);?为有量纲质量流量;U和Ac分别为叶轮叶顶线速度和管道横截面积;ρo1为空气密度。
通常,压缩机系统Greitzer模型[6]表示为:
式中 ωH为亥姆霍兹频率;B为Greitzer稳定参数;τ?为时间常数;Ψc,ss为在设计间隙下的无量纲压升。在Greitzer模型中,依据流体动量守恒定律得出Φc和Φth的微分方程,依据质量守恒定律得出Ψp的微分方程,Ψc的微分方程可表示特性曲线上工作点的动态压缩特性。
亥姆霍兹频率ωH与流体机械喘振频率大小相关,可表示为:
式中 ao1,Vp和Lc分别为压缩机入口声速、气室容积和管道长度。
式(3)中的常数G和Greitzer稳定参数B分别为:
式中 Lth与Ath分别表示节流阀的长度与横截面积。
当管道长度远大于节流阀流道长度时,常数G约等于零。当忽略时间常数时,则得到式(3)中的Greitzer模型为:
在亚声速流动条件下,可利用节流阀开度uth和气室压升Ψp表示节流阀质量流量:
式中 cth为节流阀系数。
通常由式(8)绘制的曲线称为载荷曲线或负载曲线,通过实验改变节流阀开度uth并测试压升与质量流量,可计算节流阀系数cth。
喘振点将流体机械的特性曲线分为两部分,分别为稳定运行区域和非稳定区域(喘振区域),前者通过实验测试得到,后者通过理论公式进行预测。
通过实验测试,流体机械的特性曲线可根据如下所示多项式进行拟合[35]:
式中 φc为压缩机的压比pc/po1;φc0为流量等于零时的压比pc0/po1。系数H和W可根据实验测试得到的压升和质量流量计算获取。此外,式(9)中第一项为稳定运行区域特性曲线表达式,第二项为非稳定区域特性曲线表达式。
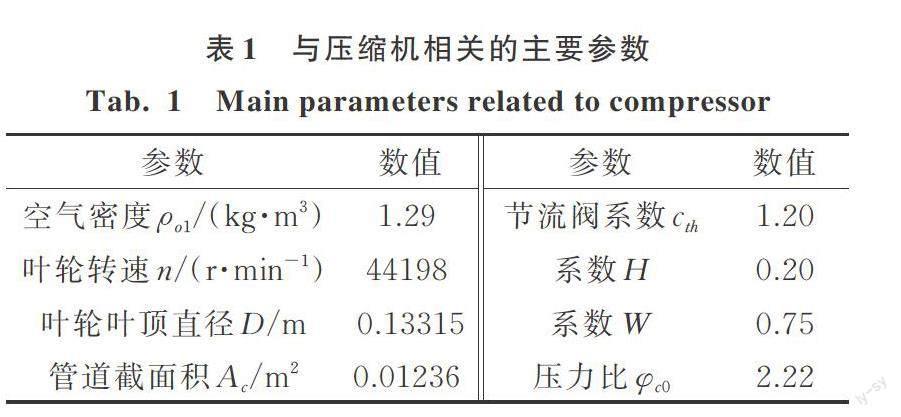
本文喘振控制仿真中,选用的流体机械为美国Honeywell公司生产的GT70单级离心式压缩机[36],将其相关的主要参数列于表1中。将表1的相关参数代入式(9)中,可得到压缩机特性曲线的表达式:
将表1中参数代入式(1)和(2)可得:
将式(11)代入式(10)中,可得无量纲特性曲线的表达式:
结合无量纲特性曲线式(12)和载荷曲线式(8),绘制压缩机无量纲特性曲线与负载曲线如图2所示。图2中,特性曲线与负载曲线的交点称为工作点。特性曲线上斜率为零的点为喘振点,在喘振点左侧,压升随着质量流量的增大而增大,表现为喘振失稳且会出现喘振环。在喘振点右侧,压升随着质量流量的增大而减小,为稳定运行状态。当节流阀开度uth=16%时,压缩机的工作点处于临界稳定状态,随着节流阀开度继续减小便会出现喘振现象。当发生喘振时,压升与质量流量均表现为周期性的振动,则会出现如图2所示的喘振环。当持续关闭节流阀,则会出现更大的喘振环,此时喘振程度加深,振动幅值变大。对比图2中15%,13%和11%三个不同节流阀开度下的喘振环,当开度减小至一定程度时(如开度为11%和13%),流量出现了负值,此时的喘振程度已经非常剧烈。
以图2中喘振状态下的节流阀开度为例,将三个开度对应的无量纲压升与质量流量的时域振动曲线绘制于图3中。由图3可知,压升与质量流量为同频率振动。此外,还可以看出,压升和质量流量的相位相差约82°,因此也导致了在特性曲线上表现为圆环。
2 叶尖间隙调压模型建立
磁悬浮流体机械喘振控制的本质是利用AMB作为作动器,控制流体机械叶轮与蜗壳间的轴向间隙,进而调整流体机械的流场分布以实现喘振控制。图4所示为磁悬浮流体机械中通常采用的半开式叶轮和叶轮叶尖间隙示意图,本文忽略叶轮背部变化对流体机械系统的影响。然而,如何使用AMB这一作动器控制叶轮的位置是喘振控制中的关键环节。
流体机械的性能和效率高度依赖于叶轮叶尖间隙,叶尖间隙对流体机械压力调节起到了关键作用,通常将叶尖间隙的变化与流体机械效率联系起来。本文采用基于叶尖间隙的调压模型,以压缩机效率变化为基础。本文仿真中选用公称叶尖间隙cln为0.6 mm,叶轮出口处的叶片高度b2为8 mm。
为了简化表达,将实际效率η表达为与叶尖间隙变化量δcl相关的形式[16]:
式中 ηn为设计效率,δcl = cl-cln,k0=0.251+0.25clnb2。
在等熵和理想气体条件下可得:
式中 γ为绝热指数。
当δcl=0时,压比φc,ss=pc,ss/po1。结合压差公式,推导得出无量纲压升关于压比的函数为:
因此,当δcl =0时:
将式(14)代入式(15)中得到:
將无量纲稳态压升表达式(16)代入式(17)中,可得无量纲压升Ψc关于Ψc, ss和δcl的函数为:
在后续喘振控制仿真中,可根据式(18)指导磁悬浮轴承作动器调节叶轮轴向悬浮位置。
根据式(18)绘制如图5所示的不同叶轮叶尖间隙对特性曲线的影响曲线。其中,图5(a)为三维曲线图,图5(b)为5个不同间隙下的压缩机特性曲线图。由图5可知,质量流量一定时,叶轮叶尖间隙越大则压升越小,这是由于间隙泄漏增大导致效率降低。
3 系统模型线性化分析
第2节中式(14)为压缩机叶轮叶尖间隙调压模型的非线性化形式,同时,前文介绍的Greitzer模型也包含非线性项。为了使控制问题得到简化,有必要对两者进行线性化。
3.1 调压模型线性化
在δcl = 0处,对式(14)中的1/(1+k0δcl / b2) 进行泰勒展开:
式中 kcl=γγ?1k0b2φ1γc,ss(1?φγ?1γc,ss)。
将式(19)中φc与φc,ss进行无量纲化,得到:
定义调压模型线性化后的误差为:
式中 Ψ'c为线性化调压模型的压升;Ψc为未线性化调压模型的压升。
将调压模型线性化误差el随质量流量和叶轮叶尖间隙的变化绘制于图6中,其中,叶轮叶尖间隙变动范围设置为±70%,质量流量变动范围设置为-0.2~0.6。在给定的叶轮叶尖间隙和质量流量波动范围内,误差el均较小,其范围约在0.03%以内。线性化误差整体较小,表明线性化模型可以代替原始非线性模型而不会损失精度。此外,由式(18)和(20)可知,在δcl = 0情况下,模型线性化前后的压升大小相等,得到如图6中所示的零误差线。
将线性化模型与原始非线性化模型下的特性曲线分别绘制于图7中,其中5对特性曲线均具有较高的重合度,即误差很小,尤其在公称叶尖间隙下误差为零。随着叶尖间隙相对公称叶尖间隙变大时,误差才逐渐有所变大,但仍然可忽略不计,正如图6所示的误差在较大范围内处于0.03%以内。因此,线性化之后的高精度可以保障后续控制器设计的顺利实施。
将线性化后的叶轮叶尖间隙调压模型代入Greitzer模型,得到含线性化调压模型的Greitzer模型为:
3.2 Greitzer模型线性化
虽然式(22)中的Greitzer模型包含线性化的叶尖间隙调压模型,但是整个系统模型仍是非线性的。
当δcl = 0时,在给定的节流阀开度ueq下,特性曲线和负载曲线的交点称为工作平衡点(Φeq, Ψeq)。定义状态变量ζi为:
在工作平衡点(Φeq, Ψeq)处,将式(23)的导数泰勒展开并代入式(23)。不计二阶及以上的高阶项,得到如下所示线性化系统模型:
式中 状态变量和系数矩阵分别为:ζ=[ζ1ζ2]和
式(24)中,将无量纲特性曲线表示为:
式中 a,b,c和d为特性曲线多项式系数。
依据线性化的Greitzer系统模型,以不同节流阀开度为变量,绘制系统的极点变化轨迹如图8所示。
由图8可知,对于二阶线性Greitzer系统,每个压缩机运行状态下均对应有一对极点。当节流阀开度逐渐减小时,系统的极点开始向右移动,开度减小至15%时开始出现了临界状态的极点。当节流阀开度大于15%时系统稳定,而小于15%则表现为失稳状态。
4 质量流量反馈的喘振控制
施加喘振控制是为了使流体机械系统能够保持稳定运行,从而使工作点处在特性曲线上。特性曲线上主要有兩个变量,分别为压升和质量流量。压升随节流阀开度的变化有增有减,而质量流量随节流阀开度的减小而减小。因此,选取后者为反馈变量实施喘振控制。
4.1 喘振控制策略
令压升和质量流量的误差为:
基于质量流量反馈的控制策略为:
式中 kp表示比例系数。
4.2 考虑轴向AMB系统的喘振控制
喘振控制实施的具体步骤为:利用喘振控制器并结合质量流量反馈信号,计算轴向磁悬浮轴承控制系统参考位置;将轴向参考位置输入AMB闭环控制系统,进行考虑实际作动器性能的计算,获得压缩机实际叶轮叶尖间隙的变化量;将间隙变化量输入至压缩机系统进行动态调整,从而影响压缩机系统中压升和质量流量的变化。上述过程即为喘振控制的一个闭环周期,如图9所示为基于质量流量反馈的喘振控制原理框图。在图9中,将喘振控制器计算的叶轮调整间隙量作为参考信号输入至悬浮控制器中,从而通过悬浮控制器参考位置的改变而改变转子轴向位置。轴向AMB采用环形单极结构,其主要参数如表2所示。
图9中AMB闭环控制系统模型的Bode图如图10所示,该模型通过将五自由度磁悬浮轴承转子系统静态悬浮后对轴向AMB闭环控制系统进行扫频得到[35]。
将PID控制器作为喘振控制器,对磁悬浮流体机械喘振控制进行仿真分析。其中,比例系数、微分系数和积分系数分别以kp,kd和ki表示,喘振控制仿真中,三者取值分别为10,0.2和0.5。
当节流阀开度分别为15%和14.5%时,得到如图11和12所示的喘振控制前后对比结果。其中,图11(a)和12(a)为给定的节流阀开度,图11(b)和12(b)以及图11(d)和12(d)分别为给定节流阀开度下压缩机压升和质量流量曲线,并给出了施加和未施加喘振控制的对比结果。图11(c)和12(c)给出了特性曲线、给定节流阀开度下的负载曲线、喘振控制与未控制时的喘振环。
在图11和12中,未施加喘振控制时,压升和质量流量出现了正弦波动,在特性曲线上表现为喘振环的形式。节流阀开度越小,振动的幅值越大。施加喘振控制后,压升和质量流量在小幅度波动后可快速达到稳定状态,调节时间在0.14 s以内且开度越小调节时间越长。在稳定状态下,压缩机的工作点为特性曲线和负载曲线的交点,图11和12中的最终稳定工作点分别为(0.295, 2.680)和(0.285, 2.674)。
图13对比了喘振控制器未施加与施加情况下,压升和质量流量随节流阀开度变化的频谱图。仿真中,以0.5%的节流阀开度为步长,仿真分析10%~20%节流阀开度范围内的控制效果。由图13可知,在未施加喘振控制情况下,当开度为15%时便会出现压升与质量流量的波动。然而,在控制情况下,当开度为13.5%时才开始出现压升与质量流量的波动,即发生喘振。因此,当施加控制时,可以扩展流体机械的稳定运行范围,由未控制下的15.5%开度扩展至控制下的14%。此外,由图13可以看出,喘振振动的频率约为24 Hz,后续会针对喘振频率进行辨识研究。
为了更深入地对磁悬浮流体机械的喘振控制进行研究,后续分别针对喘振频率辨识和喘振控制器中不同控制参数进行控制规律研究。
4.3 喘振频率辨识
为了对流体机械系统进行喘振频率的辨识,仿真测试了叶轮叶尖间隙扰动对压升的动态影响。对于小幅值正弦扫频输入,分析了压升信号对叶轮叶尖间隙扰动的频率响应。图14给出了正弦扫频原理框图,在叶轮悬浮位置输入小幅值、变频率正弦信号,频率步长设置为1 Hz,喘振控制器控制参数为kp=1,ki=0,kd=0,采集压缩机系统的压升信号。
如图15所示,在线性系统中,压升信号响应频率与输入扰动频率之间存在较强的对应关系。图15中的压升信号虽然也表现出了微弱的2倍频分量,但相对于同频分量可以忽略。
通过不同频率的小幅值正弦信号扰动,得到如图16所示的不同节流阀开度下的Bode图。可以看出,开度为20%,30%和40%状态下表现为过阻尼状态,而图16中其他开度下则可以展现出明显的喘振频率。当节流阀开度为16%,17%和18%时,在25 Hz附近为压力波动峰值,由此判断,该频率为喘振频率,与仿真中亥姆霍兹频率ωH的理论设定值161.36 rad/s(25.68 Hz)基本一致。同样,实际工业现场也可根据此方法以判断磁悬浮流体机械的喘振频率。然而,由图16还可以看出,当开度为15%时,喘振频率为24 Hz,这是由于16%的节流阀开度为压缩机临界稳定开度,而开度为15%时已经发生了喘振。喘振频率随着节流阀开度的变化而发生少许变化是可以接受的,工程实践中的喘振频率在小范围内波动也是合理的。
4.4 喘振控制器不同控制参数的影响研究
以PID喘振控制器为例,分析各控制参数的影响。图17所示为控制器中比例系数kp对压缩机系统压升与质量流量的影响曲线。在仿真中,为了观察比例系数kp的作用,将微分系数和积分系数均设置为0,并将节流阀开度设置为14%(喘振状态)。通过将比例系数由0逐渐变化至10,进行多组仿真得到如图17所示结果。图17中,当kp=7.0时停止喘振。可以看出,随着比例系数kp的增大,压升与质量流量的波动幅值近乎线性减小,最后喘振波动逐渐消失。
图18为控制器中微分系数kd对压缩机系统压升与质量流量的影响曲线。在仿真中,为了观察微分系数kd的作用,令比例系数kp=1、积分系数ki=0,并将开度设置为14%(喘振状态)。通过将微分系数由0逐渐变化至0.15,进行多组仿真得到如图18所示结果。图18中,当kd=0.075时停止喘振。可以看出,当仅有kp=1作用时,不能有效地控制喘振状态,而随着微分系数kd的增大,压升与质量流量的波动幅值近乎线性减小,最后喘振波动逐渐消失。
图19所示为控制器中积分系数ki对压缩机系统压升与质量流量的影响曲线。在仿真中,令比例系数kp=0.5、微分系数kd=0.2,并将节流阀开度设置为14%(喘振状态)。可以看出,随着积分系数ki的增大,压升与质量流量均未出现明显变化,这是由于此时在比例系数和微分系数的作用下系统已经处在稳定状态。因此,积分系数仅仅起到将静态误差减小的作用。
图20所示为在图19情况下,叶轮叶尖间隙调节位移随积分系数ki变化的曲线。随着积分系数ki的增大,调节位移量逐渐变大,用以抵消质量流量的静态误差。
综上所述,三个控制参数的调节直接影响喘振控制效果。其中,比例系数和微分系数起到稳定流体机械运行状态的关键作用,而积分系数在系统稳定的前提下,可使质量流量的静态误差进一步减小。
5 结 论
依据流体机械系统Greitzer模型,得到了叶轮叶尖间隙调压模型。为了便于控制器设计与控制分析,对非线性模型进行了线性化处理,在设定的调节间隙内误差仅在0.03%以内。采用了质量流量的反馈控制方法,将軸向AMB系统作为作动器进行喘振控制仿真。仿真结果表明,在给定PID喘振控制器控制参数下,扩展了流体机械的稳定运行范围,稳定状态由未控制下的15.5%节流阀开度扩展至喘振控制下的14%。仿真测试了叶轮叶尖间隙扰动对压升的动态影响,分析了压升信号对叶轮叶尖间隙小幅值正弦扫频扰动的频率响应,辨识得出流体机械系统模型的喘振频率约为25 Hz,与理论设定的亥姆霍兹频率ωH数值161.36 rad/s(25.68 Hz)基本一致。为更深入地对磁悬浮流体机械的喘振控制进行研究,针对PID喘振控制器中不同控制参数进行了研究,研究结果表明,随着比例系数kp和微分系数kd的增大,压升与质量流量的波动幅值近似线性减小,最后喘振波动逐渐消失,而积分系数仅起到将静态误差减小的作用。
参考文献
1Gravdahl J T, Egeland O. Compressor Surge and Rotating Stall: Modeling and Control[M]. London: Springer, 1999.
2Kurz R, White R C. Surge avoidance in gas compression systems[J]. Journal of Turbomachinery, 2004, 126(4): 501-506.
3Shafieian M, Zavar M, Rahmanian M. Simulation and control of surge phenomenon in centrifugal compressors[J]. Traitement du Signal, 2019, 36(3): 259-264.
4Badmus O O, Nett C N, Schork F J. An integrated, full-range surge control/rotating stall avoidance compressor control system[C]. American Control Conference, Boston, MA, 1991: 3173-3180.
5Emmons H W, Pearson C E, Grant H P. Compressor surge and stall propagation[J]. Transactions of the ASME, 1955, 77(4): 455-469.
6Greitzer E M. Surge and rotating stall in axial flow compressors-part I: theoretical compression system model[J]. Journal of Engineering for Gas Turbines and Power, 1976, 98(2): 190-198.
7Hansen K E, J?rgensen P, Larsen P S. Experimental and theoretical study of surge in a small centrifugal compressor[J]. Journal of Fluids Engineering, 1981, 103(3): 391-395.
8Moore F K, Greitzer M E. A theory of post-stall transients in axial compression systems: part I-development of equations[J]. Journal of Engineering for Gas Turbines and Power, 1986, 108(1): 68-76.
9Ishii H, Kashiwabara Y. A numerical study of surge and rotating stall in axial compressors[C]. The 27th Joint Propulsion Conference. Sacramento, CA, 1991: 1-8.
10Feulner M R, Hendricks G J, Paduano J D. Modeling for control of rotating stall in high speed multi-stage axial compressors[J]. Journal of Turbomachinery, 1994, 118(1): 1-12.
11杜毅, 宋欣達, 韩邦成. 高速磁悬浮鼓风机系统模型改进与实验[J]. 振动、测试与诊断, 2019, 39(3): 512-517.
DU Yi, SONG Xinda, HAN Bangcheng. Improvement and experimental research on high-speed magnetic blower and pipeline system[J]. Journal of Vibration, Measurement & Diagnosis, 2019, 39(3): 512-517.
12Boinov K O, Lomonova E A, Vandenput A J A, et al. Surge control of the electrically driven centrifugal compressor[J]. IEEE Transactions on Industry Applications, 2006, 42(6): 1523-1531.
13Chaturvedi N A, Bhat S P. Output-feedback semiglobal stabilization of stall dynamics for preventing hysteresis and surge in axial-flow compressors[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 301-307.
14Senoo Y. Pressure losses and flow field distortion induced by tip clearance of centrifugal and axial compressors[J]. JSME International Journal, 1987, 30: 375-385.
15Senoo Y, Ishida M. Deterioration of compressor performance due to tip clearance of centrifugal impellers[J]. Journal of Turbomachinery, 1987, 109(1): 55-61.
16Sanadgol D. Active control of surge in centrifugal compressors using magnetic thrust bearing actuation[D]. Charlottesville: The University of Virginia, 2006.
17Ahn H J, Park M S, Sanadgol D, et al. A pressure output feedback control of turbo compressor surge with a thrust magnetic bearing actuator[J]. Journal of Mechanical Science and Technology, 2009, 23(5): 1406-1414.
18Yoon S Y, Lin Z L, Lim K T, et al. Model validation for an active magnetic bearing based compressor surge control test rig[J]. Journal of Vibration and Acoustics, 2010, 132(6): 061005.
19Yoon S Y, Lin Z L, Goyne C, et al. An enhanced Greitzer compressor model with pipeline dynamics included[C]. American Control Conference, San Francisco, 2011: 4731-4736.
20宋海成. 離心式压缩机的防喘振控制[J]. 自动化技术与应用, 2015, 34(12): 9-14.
SONG Haicheng. Anti surge control of centrifugal compressor[J]. Industry Control and Applications, 2015, 34(12): 9-14.
21Spakovsky Z S, Paduano J D, Larsonneur R, et al. Tip clearance actuation with magnetic bearings for hig-speed compressor stall control[J]. Journal of Turbomachinery, 2001, 123(3): 464-472.
22Wang Y, Paduano J D, Murray R M. Nonlinear control design for rotating stall with magnetic bearing actuators[C]. IEEE International Conference on Control Applications. Kohala Coost, HI, 1999: 730-736.
23Sanadgol D, Maslen E. Effects of actuator dynamics in active control of surge with magnetic thrust bearing actuation[C]. IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, California, 2005: 1091-1096.
24Lim K T, Yoon S Y, Goyne C P, et al. Design and characterization of a centrifugal compressor surge test rig[J]. International Journal of Rotating Machinery, 2011, 2011: 738275.
25Yoon S Y, Lin Z L, Allaire P E. Control of Surge in Centrifugal Compressors by Active Magnetic Bearings[M]. London: Springer, 2012.
26Yoon S Y, Lin Z L, Allaire P E. Experimental evaluation of a surge controller for an AMB supported compressor in the presence of piping acoustics[J]. IEEE Transactions on Control Systems Technology, 2014, 22(3): 1215-1223.
27Yoon S Y, Lin Z L, Jiang W, et al. Flow-rate observers in the suppression of compressor surge using active magnetic bearings[J]. Journal of Turbomachinery, 2013, 135(4): 041015.
28Sanadgol D, Maslen E. Backstepping for active control of surge in unshrouded centrifugal compressors with magnetic thrust bearing actuation[C]. Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air. Reno, NV,2005: 883-889.
29Sanadgol D, Maslen E. Sliding mode controller for active control of surge in centrifugal compressors with magnetic thrust bearing actuation[C]. The 9th International Symposium on Magnetic Bearings, Lexington, 2004.
30Anantachaisilp P, Lin Z L. Fractional-order surge control of active magnetic bearings suspended compressor[J]. Actuators, 2020, 9(3): 9030075.
31Yoon S Y. Surge control of active magnetic bearing suspended centrifugal compressors[D]. Charlottesville: The University of Virginia, 2011.
32唐茂, 周瑾, 崔恒斌. 磁懸浮离心式压缩机的推力轴承喘振控制[J]. 自动化仪表, 2017, 38(5): 15-19.
TANG Mao, ZHOU Jin, CUI Hengbin. Surge control of the centrifugal compressor with magnetic thrust bearing[J]. Process Automation Instrumentation, 2017, 38(5): 15-19.
33Guan X D, Zhou J, Jin C W, et al. Influence of different operating conditions on centrifugal compressor surge control with active magnetic bearings[J]. Engineering Applications of Computational Fluid Mechanics, 2019, 13(1): 824-832.
34Ma X, Zheng S Q, Wang K. Active surge control for magnetically suspended centrifugal compressors using a variable equilibrium point approach[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9383-9393.
35唐茂. 离心式压缩机的磁悬浮喘振控制研究[D]. 南京:南京航空航天大学, 2017.
TANG Mao. Active control of surge in centrifual compressors by magnetic actuation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017.
36李瑭珺. 离心压缩机喘振模型与稳定性分析[D]. 上海: 上海交通大学, 2011.
LI Tangjun. Surge modeling and stability analysis in centrifugal compressors[D]. Shanghai: Shanghai Jiao Tong University, 2011.
Surge control of magnetic suspension fluid machinery
GUAN Xu-dong 1 ?ZHOU Jin 2 ?JIN Chao-wu 2XU Yuan-ping 2TANG Mao 3CUI Heng-bin 2
1. Department of Mechanical and Electronic Engineering, School of Mechanical Engineering and Rail Transit, Changzhou University, Changzhou 213164, China;
2. Department of Design Engineering, College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. CSIC(Chongqing) Southwest Equipment Research Institute Co.,Ltd., Chongqing 401123,China
Abstract Aiming at the surge problem of magnetic suspension fluid machinery, a surge control strategy based on mass flow is adopted according to the fluctuation of mass flow and pressure rise in the surge state of fluid machinery system. Specifically, the surge controller is used to calculate the axial adjustment clearance of the impeller. It is input into the closed-loop control system of the axial magnetic bearing as the reference signal of the suspension position, to change the axial position of the magnetic suspension fluid mechanical rotor under the action of the axial magnetic bearing system. The tip clearance of the impeller is changed to realize the active control of surge. The simulation results show that when surge control is applied, the stable operation range of fluid machinery can be extended from 15.5% throttle valve opening under uncontrolled control to 14% under surge control. The surge frequency is identified by simulating excitation, and the influence of control parameters in PID controller on surge control performance is studied.
Keywords surge control; magnetic suspension fluid machinery; magnetic bearing; mass flow

