随机振动下产品包装系统传递路径分析
陈俊菲 张元标 林聪


摘要 实验研究不同激励谱型、不同振动等级、不同缓冲衬垫厚度和不同衬垫分配方式下产品包装系统的振动响应规律,利用工况传递路径分析法(OTPA)量化随机振动下产品包装系统各传递路径的振动贡献量。结果表明:当振动等级较高时,包装件出现轻微跳动现象,系统振动响应增大,共振频率略微减小;随着缓冲衬垫厚度的增加,系统共振频率减小,不同激励谱下关键元件的加速度响应功率谱密度(PSD)有所差异,振动响应与系统共振频率处的激励能量大小有关,衬垫厚度对各路径的振动贡献量影响较小;衬垫分配方式对关键元件上的响应PSD影响较大,不同衬垫分配方式可调节各传递路径的振动贡献量大小;当缓冲衬垫面积均匀分配时,利用OTPA方法识别出系统的主要振动贡献路径,将其定义为关键振动传递路径,关键元件的响应与关键振动传递路径在共振频率附近的振动贡献量紧密相关,缓冲包装设计应重点关注关键振动传递路径的减振设计。研究结果为进一步研究缓冲包装设计方法提供理论支撑。
关键词 随机振动; 包装系统; 功率谱密度; OTPA; 振动贡献量
引 言
在公路物流运输过程中,路面不平、行驶突变等会产生随机振动信号。缓冲包装是保护产品的有效形式,通过确定产品所需的缓冲衬垫厚度和面积,以保护产品、减少产品受到来自随机激励的损害。实际物流中的产品形状、结构通常是不规则的,产品重心偏置、各零件材料结构的差异会导致从产品底部至关键元件处的各路径振动传递能力不同,而不同缓冲衬垫面积大小的减振效果差异较大,合理地分配各角垫处缓冲衬垫面积是对缓冲包装设计的完善和补充。
国内外学者对随机振动下产品包装系统的动态响应做了大量研究,主要集中在产品包装件随机振动实验研究和有限元分析验证上[1?6]。部分学者对产品包装系统内各振动路径传递能力的差异性展开了讨论。文献[7?9]通过力锤实验,应用逆子结构多点耦合法对产品运输系统进行研究,发现产品和包装的四个耦合点在不同频率下对产品的振动贡献率是不同的。王启利等[10]研究了包装耦合界面的物理参数对路径贡献的影响,得到产品运输系统各种结构承载路径的主要控制因素和贡献。
传递路径分析(TPA)是分析结构振动、噪声传递的重要工具,常用于分析各传递路径的振动贡献量,以识别出主要振动贡献路径[11?14]。工况传递路径分析方法(OTPA)由TPA发展而来,以简便、快捷著称,极大地缩短了测试与建模时间[15?17]。在实际公路运输工况下,研究产品包装系统内不同传递路径的振动贡献是具有重要意义的。本文以不规则产品包装系统模型为研究对象,应用OTPA方法作为振动传递路径分析的主要工具,识别出产品包装系统的主要振动贡献路径,量化分析不同衬垫分配方式下各路径的振动贡献量。根据分析结果,合理地分配各角垫处的衬垫面积,精确地设计缓冲包装结构,在达到相同缓冲和减振效果的条件下,节省缓冲材料,减少货物在运输过程中的经济损失。
1 随机振动试验方法
1.1 产品包装系统参数
实验用的产品模型和缓冲衬垫如图1所示。产品由三个质量块构成,其中顶块为产品的关键元件,产品的具体尺寸和质量如表1所示。缓冲材料为发泡聚乙烯泡沫(EPE),选用20,30和40 mm三种不同厚度的EPE作缓冲衬垫,密度分别为14.3, 16.7和15.7 kg/m3,采用五种不同衬垫分配方式进行包装,各分配方式下缓冲衬垫的总缓冲面积均为144 mm2。不同衬垫分配方式在各角垫处的缓冲面积不同,四块角垫分为两组:A组衬垫和B组衬垫,同组衬垫的尺寸一致,两组衬垫的长度在不同分配方式下均相同,均为90 mm,从分配方式1至分配方式5,A组衬垫的宽度逐渐变窄,B组衬垫的宽度逐渐变宽,如图2所示。不同分配方式下缓冲衬垫尺寸如表2所示。
通过缓冲衬垫扫频实验[18]和半功率带宽法[19]得到不同厚度EPE缓冲衬垫的刚度和阻尼,如表3所示。随着缓冲衬垫厚度的增加,缓冲衬垫的刚度和阻尼均减小。
1.2 试验设备和方法
采用美国Lansmont公司振动测试系统(Model 7000—10)对产品包装系统进行随机振动实验,TVT系统用于控制振动台,DASP系统用于采集时域信号,如图1所示。采用美国材料与试验协会(ASTM)中的D4169—16测试标准中的卡车激励谱作为随机激励[20],共3个振动等级,分别为Level 1,Level 2和Level 3,其中Level 1为高强度等级,Level 2为中强度等级,Level 3为低强度等级。为探究激励谱谱型对产品动态响应的影响,添加了一组限带白噪声激励谱作为对比[4],为保证两种谱型的总体振动强度相同,两种激励谱的各振动等级的加速度均方根值均相等,两种功率谱密度谱型如表4,5和图3所示。
将产品包装系统置于振动台中央,在P1, P2, P3, P4和产品顶块处分别安装加速度传感器,同时将加速度传感器与时域数据采集仪DASP相连接,P1, P2, P3, P4位置见图1。在振动过程中,产品与衬垫可能因随机激励过大而脱离,影响响应结果的准确性,需用少量双面胶固定产品与衬垫。每组实验振动持续时间为2 min,采样频率为1024 Hz,记录产品P1, P2, P3, P4和关键元件的加速度响应。调用MATLAB中的Pwelch函数进行功率谱密度的计算,对每一段信号进行加窗处理,设置每段数据长度为1024,汉宁窗加窗数为512,每段数据的重叠长度为256。
2 随机振动结果分析
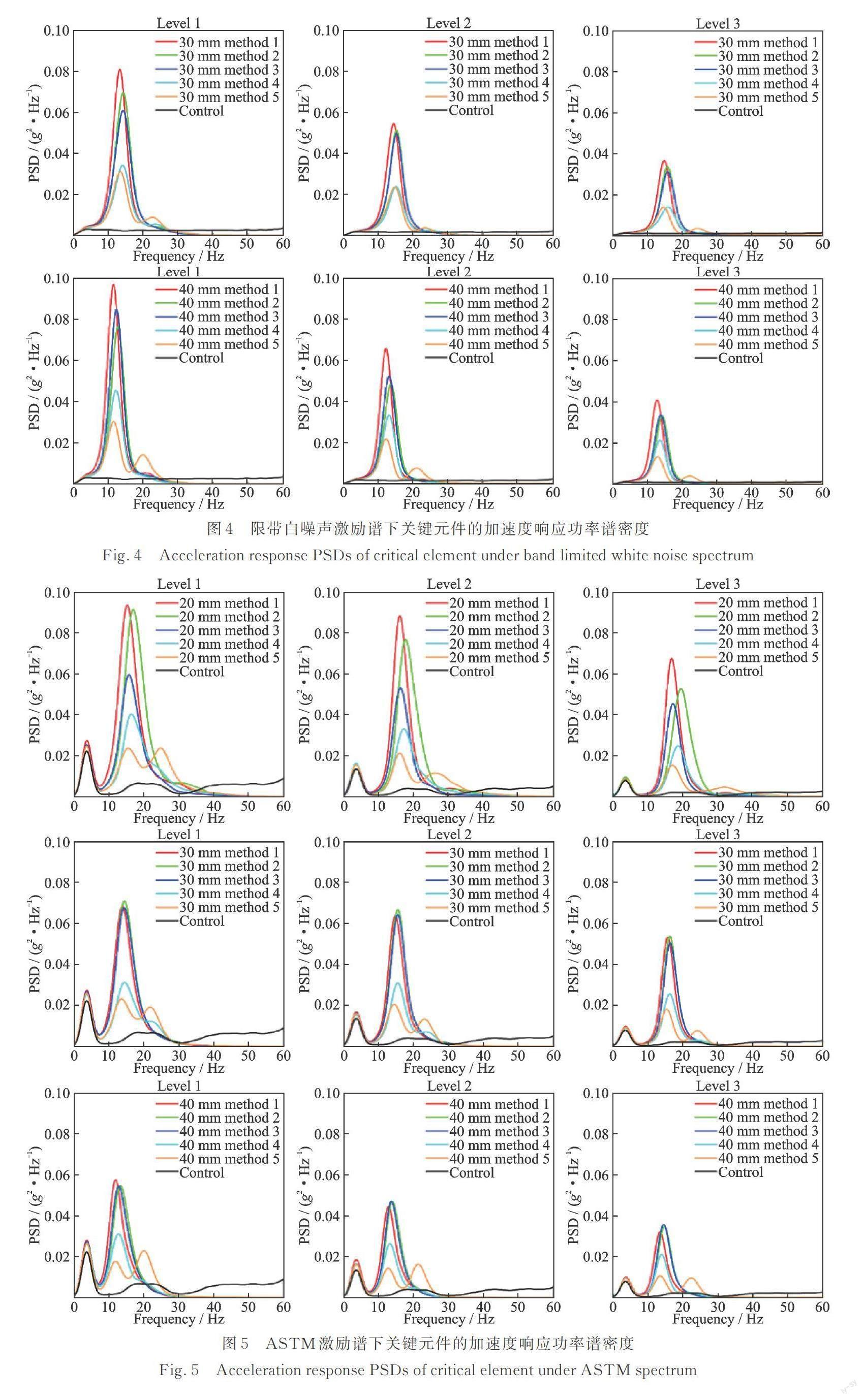
关键元件上响应能量集中在0~60 Hz频段内, 响应PSD曲线仅展示0~60 Hz频段的曲线。在两种激励谱型、三种振动等级、三种缓冲垫厚度和五种缓冲衬垫分配方式下关键元件上加速度响应功率谱密度如图4和5所示。在两种功率谱下,响应PSD曲线在缓冲衬垫分配方式1, 2, 3和4下仅有一个共振峰,在分配方式5下,关键元件上高阶共振峰被激发出来,方式5的一阶共振峰值明显低于方式1, 2, 3, 4的一阶共振峰值,关鍵元件上的加速度响应PSD主要由一阶共振峰控制。
三种振动等级下的结果对比:随着振动强度从Level 3增加到Level 1,关键元件上的加速度响应PSD整体增大,共振频率随着激励谱振动强度等级的增加而逐渐减小,外部激励强度的增加会引起产品包装系统的跳动,导致缓冲衬垫的等效刚度降低,从而出现共振频率左移的现象。
三种缓冲垫厚度和两种功率谱下的结果对比:两种激励谱下,响应PSD随厚度增加的动态表现不同,关键元件上的加速度响应大小由产品包装系统的自身振动传递特性和共振频率附近的激励谱能量大小共同控制。在ASTM激励谱下,关键部件上的加速度响应PSD值随着衬垫厚度的增加而减小,而在带限白噪声激励谱下,情况则相反。这是由于衬垫厚度的增加会导致其刚度降低,产品包装系统的共振频率随着衬垫刚度的降低而逐渐减小,响应PSD曲线趋于尖锐。不同厚度和分配方式下产品包装系统的共振频率在12~18 Hz之间,白噪声激励谱在该频段的能量保持不变,而ASTM激励谱能量在该频段内处于逐渐增加的状态。在ASTM激励下,较厚的缓冲衬垫下产品包装系统在共振频率附近受到的激励能量较小,此时关键元件的加速度响应也较小,厚衬垫的减振效果更好。
不同的缓冲衬垫分配方式下的结果对比:不同分配方式的减振效果差异较大,关键元件的加速度响应PSD大小随着分配给P3和P4位置处的缓冲面积增加而减少。在衬垫分配方式4和5下,关键元件的响应PSD远小于衬垫分配方式1,2,3下的响应PSD,缓冲衬垫分配方式4和5的缓冲减振效果更为显著。为了探究导致不同衬垫分配方式下减振效果差异的原因,将通过传递路径分析作进一步的讨论。
3 振动传递路径分析方法
3.1 工况传递路径分析方法
根据OTPA理论,假设系统是线性的,输入信号和输出信号的关系可以表示为[21]:
式中 H(jω)为传递函数矩阵;X(jω)为激励矩阵;Y(jω)为响应矩阵。
在OTPA方法中,式(1)中的输入信号和输出信号在工况下被同时测量,工况下的传递函数矩阵H(jω)成为传递率矩阵A,即可得到下式:
矩阵表达式为:
式中 r为测试工况数;m为路径数;n为数据采集点数,那么传递率矩阵可以表达为:
然而,在大多数情况下,输入矩阵不是方阵(即m≠n)。在这种情况下,可用最小二乘法求得传递函数矩阵:
式中 X+为输入矩阵X的伪逆矩阵,且X+=(XTX)?1XT。为了使式(5)可解,测试工况数目需大于传递路径数,即r>m。
由于参考输入信号存在相互耦合的现象,直接求解得到传递函数可能会存在一定误差,可采用奇异值分解(SVD)来确定输入矩阵X+的伪逆,即:
式中 U,V为酉矩阵;Λ为对角方阵; Λ称为X的奇异值矩阵,得到伪逆矩阵X+为:
得到奇异值分解后的传递率矩阵为:
合成响应Y?可根据目标工况下输入信号矩阵X计算得到:
各路径的振动贡献为:
3.2 OTPA振动传递模型
在随机振动实验中,振动台产生的随机激励信号通过4个缓冲衬垫传递到产品的底部,然后经由产品底部传递至关键元件上,构成了产品包装系统的4条振动传递路径,P1,P2,P3,P4位置处的振动加速度为输入变量,关键元件上的振动加速度为输出变量,构成了多输入单输出的振动传递模型,如表6所示。
3.3 OTPA工况条件
选择合适的运行工况是OTPA传递路径研究的一个关键点,通过改变随机激励谱的谱型和振动强度等级来改变产品底部P1,P2,P3,P4和关键元件处的动态响应,测取P1,P2,P3,P4和关键元件处的加速度响应时域信号,利用傅里叶变换得到加速度响应频域信号,通过式(8)计算得到4条振动传递路径的传递率矩阵。
测试工况用于计算4条路径的振动传递率矩阵,利用振动传递率矩阵来分析目標工况下各路径的振动贡献量。ASTM激励谱更能反映产品包装系统在实际公路路况下所历经的随机过程,中等强度等级Level 2的应用范围较广,因此本文选择ASTM激励谱Level 2振动强度等级作为目标工况,分析该工况下各路径的振动贡献量。测试工况包含2种类型和3种强度等级的随机激励谱,共5种测试工况。测试工况和目标工况列于表7中,满足测试工况数量大于振动传递路径数量的要求。
4 随机振动下传递路径分析
应用OTPA方法对随机振动下的各路径进行振动贡献分析,根据测试工况下测得的传递率矩阵和目标工况下的输入矩阵,合成关键元件上的输出信号,与实测信号进行比较,以验证OTPA计算得到的传递函数矩阵的正确性。图6对比了ASTM卡车运输谱Level 2下的关键元件上响应加速度频域信号的合成值与实验值。结果表明:在不同衬垫分配方式和衬垫厚度下,合成值曲线和实验值曲线的趋势均保持一致,两者吻合程度高,验证了OTPA方法应用于产品包装系统传递路径分析的正确性。
不同分配方式下各路径的振动贡献量差异较大,厚度对路径的振动贡献量影响不明显,如图7所示。在分配方式1下,路径3和4的振动贡献量远大于路径1和2的振动贡献量,这表明缓冲衬垫面积均匀分配时,产品包装系统的4条振动传递路径的振动传递能力不同,其中路径3和4为产品包装系统的主要振动贡献路径,将路径3和4定义为系统的关键振动传递路径,在进行包装设计时,应该重点关注关键振动传递路径的减振设计。
关键元件上的响应大小与关键振动传递路径在共振频率附近的振动贡献量大小紧密相关。相较于分配方式1,分配方式2和3在关键振动传递路径上分配了更大的衬垫面积,但关键振动传递路径上的振动贡献量没有明显变化,导致前三种分配方式下关键元件上的响应变化不大。在分配方式4和5下,路径1和2的振动贡献量超过路径3和4,成为系统的主要振动贡献路径。在分配方式5下,路径1和路径2的响应激发出二阶共振峰,致使关键元件的加速度响应PSD也产生了二阶共振频率。当衬垫分配方式为4和5时,关键振动传递路径处的衬垫面积进一步增加,经过缓冲衬垫传递至关键振动传递路径P3和P4处的激励减少,关键振动路径上传递的总能量减少,而路径1和路径2上传递的能量增多,实现了能量转移,此时缓冲衬垫的减振效果较好。
共振频率处各路径的振动贡献量是各路径振动传递能力的重要体现,降低共振频率处路径的振动贡献量是实现减振包装设计非常关键的一步。在不同厚度和缓冲衬垫分配方式下,各路径在共振频率处的振动贡献量如图8所示。
在共振频率处各路径的振动贡献量差异较为显著。在分配方式1, 2, 3下,关键振动传递路径(路径3和路径4)在共振频率处的振动贡献量为路径1和路径2振动贡献量总量的3~5倍;在缓冲衬垫分配方式4和5下,路径1和2在共振频率处的振动贡献量总量为关键振动传递路径振动贡献量的3~6倍。不同分配方式下,在共振频率处各路径的振动贡献总量差距较大,分配方式1, 2, 3下各路径的振动贡献总量远大于分配方式4和5下各路径的振动贡献总量。
为了宏观地描述在频域范围ω1~ω2内,通过第p条路径传递到关键元件上的振动贡献量,定义在随机振动下频段内ω1~ω2总振动贡献量为:
通过对?(p)ω1:ω2的定义,可以评价频段ω1~ω2内,第p条路径在随机振动下的振动传递的总体能力,用于指导缓冲包装设计。关键元件上各路径在频段0~60 Hz的振动贡献如图9所示。
在分配方式1, 2, 3下,关键振动传递路径在0~60 Hz频段的总振动贡献量为路径1和路径2的总振动贡献之和的1.4倍以上;在缓冲衬垫分配方式4和5下,路径1和路径2在0~60 Hz频段的总振动贡献之和为关键振动传递路径的2倍以上。随着缓冲衬垫厚度的增加,不同分配方式下各路径的0~60 Hz频段总振动贡献量减小,这与加速度响应功率谱密度结果一致。
5 结 论
本文研究了随机振动下振动等级、加速度功率谱谱型、缓冲衬垫厚度和衬垫分配方式对产品包装系统中关键元件振动响应的影响,分析和量化了各传递路径的振动贡献量,得到以下结论:
(1)振动强度等级、缓冲衬垫厚度和分配方式对产品包装系统的振动响应有显著的影响。系统的共振频率随着缓冲衬垫厚度和振动等级的增加而减小。在不同激励谱下,衬垫厚度对关键元件上动态响应的影响不同,关键元件上的加速度响应大小由产品包装系统的自身振动传递特性和共振频率附近的激励谱能量大小共同控制。保持衬垫面积大小不变,改变衬垫分配方式,向局部角垫处分配更多的衬垫面积时,可减小关键元件的振动响应。
(2)利用OTPA方法分析了随机振动下产品包装系统各路径的振动贡献量,关键元件上响应信号的合成值与实测值吻合程度高,验证了该方法的正确性,为进一步研究缓冲包装设计方法提供理论支撑。应用OTPA方法,识别出衬垫面积均匀分配时产品包装系统的主要振动贡献路径,将其定义为系统的关键振动传递路径,其共振频率处振动贡献量和0~60 Hz频段总振动贡献量均大于其他路径,减振包装设计应重点关注关键振动传递路径。
(3)产品内部各路径的振动传递能力难以轻易改变,调整衬垫面积的分配方式可减少关键振动传递路径的振动贡献量,增大其他传递路径的振动贡献量,实现能量转移,从而达到减振目的。随着更多的缓冲面积分配到关键振动传递路径上,关键振动传递路径上在共振频率处的振动贡献量和0~60 Hz频段的总振动贡献量均减小,关键元件的加速响应也明显减小。关键元件的响应大小与关键振动贡献路径在共振频率附近的振动贡献量大小紧密相关。
参考文献
1朱大鹏, 魏洁. 包装件振动可靠性的不确定度量化及灵敏度分析[J]. 振动与冲击, 2021, 40(3): 204?211.
ZHU D P, WEI J. Uncertainty quantification and sensitivity analysis of package vibration reliability[J]. Journal of Vibration and Shock, 2021, 40(3): 204-211.
2王志伟, 伍炼. 托盘运输包裝单元冲击响应的试验与有限元分析[J]. 振动与冲击, 2021, 40(16): 124-131.
WANG Z W, WU L. Experimental and finite element analysis of the impact response of a pallet transport packaging unit[J]. Journal of Vibration and Shock, 2021, 40(16): 124-131.
3王志伟, 房树盖. 不同谱型激励下包装件动态响应研究[J]. 振动与冲击, 2019, 38(24): 218-226.
WANG Z W, FANG S G. A study on dynamic responses properties of packaged products under different spectral excitation[J]. Journal of Vibration and Shock, 2019, 38(24): 218-226.
4孙君, 王志伟. 啤酒瓶周转箱随机振动响应的实验研究[J]. 振动工程学报,2018, 31(5): 759-771.
SUN J, WANG Z W. Experimental investigation of dynamic response of beer bottle-turnover boxes in random vibration[J]. Journal of Vibration Engineering, 2018, 31(5): 759-771.
5钟琳琳. 啤酒瓶周转箱运输单元随机振动的有限元分析和试验验证 [D]. 广州:暨南大学, 2019.
Zhong Linlin. Finite element analysis and experiment verification on the random vibration of transport unit of beer bottle-turnover boxes[D]. Guangzhou: Jinan University, 2019.
6李晓刚. 运输包装系统随机振动频域分析[J]. 包装工程, 2012, 33(15): 50-54.
LI X G. Random vibration frequency domain analysis of transport packaging system[J]. Packaging Engineering, 2012, 33(15): 50-54.
7WANG Z W, WANG J, ZHANG Y B, et al. Application of the inverse substructure method in the investigation of dynamic characteristics of product transport system[J]. Packaging Technology and Science, 2012, 25(6): 351-362.
8ZHANG Y B, WANG Z W. Investigation of frequency response function of product-transport system based on multi-coordinate coupled inverse substructure method[J]. Packaging Technology and Science, 2014, 27(5): 364-375.
9WANG Z W, ZHANG Y B. Dynamic characteristic analysis of refrigerator-truck transport system by using inverse substructure method[J]. Packaging Technology and Science, 2014, 27(11): 883-900.
10王启利, 王军. 基于逆子结构的产品包装耦合系统传递路径分析[J]. 包装工程, 2015, 36(19): 7-12.
WANG Q L, WANG J. Transfer path analysis of product packaging system based on dynamic inverse sub-structuring theory[J]. Packaging Engineering, 2015, 36(19): 7-12.
11舒俊成, 贺尔铭. 振动传递路径频域分析方法研究进展[J]. 机械科学与技术, 2020, 39(11): 1647-1655.
SHU J C, HE E M. Review on vibration transfer path analysis methods in frequency domain[J]. Mechanical Science and Technology for Aerospace Engineering, 2020, 39(11): 1647-1655.
12TAN J J, CHAIGNE A, ACRI A. Operational transfer path analysis of a piano[J]. Applied Acoustics, 2018, 140: 39-47.
13LEE D, LEE J W. Operational transfer path analysis based on deep neural network: numerical validation[J]. Journal of Mechanical Science and Technology, 2020, 34(3): 1023-1033.
14Putner J, Lohrmann M, Kaltenhauser A. Operational transfer path analysis predicting contributions to the vehicle interior noise for different excitations from the same sound source[C]. 41st International Congress and Exposition on Noise Control Engineering 2012. New York: INTER-NOISE, 2012: 9849-9860.
15CHENG W, BLAMAUD D, CHU Y, et al. Transfer path analysis and contribution evaluation using SVD- and PCA-based operational transfer path analysis[J]. Shock and Vibration, 2020, 2020: 1-23.
16姜少瑋. 基于工况传递路径分析方法的车内噪声识别研究[D]. 沈阳:沈阳理工大学, 2019.
Jiang Shaowei. Based on operational transfer path analysis method research on identification of vihicle interior noise[D]. Shenyang: Shenyang Ligong University, 2019.
17DE SITTER G, DEVRIENDT C, GUILLAUME P, et al. Operational transfer path analysis[J]. Mechanical Systems and Signal Processing, 2010, 24(2): 416-431.
18馮涛, 苏彬, 刘斌, 等. 泡沫材料厚度对其刚度及阻尼系数的影响[J]. 包装工程, 2012, 33(9): 37-40.
FENG T, SU B, LIU B, et al. Experimental research of influences of foam material thickness on its stiffness and damping coefficient[J]. Packaging Engineering, 2012, 33(9): 37-40.
19RENJI K, DIVYA K, JOSEPH T K. Effect of sine sweep on the damping factor estimated through half-power bandwidth method[J]. Advances in Vibration Engineering, 2011, 10(2): 149-156.
20ASTM. Standard practice for performance testing of shipping containers and systems: ASTM D4169—2022[S]. ASTM,2016.
21陈克, 房旭. 基于OTPA方法的乘用车路面噪声传递路径分析[J]. 沈阳理工大学学报, 2020, 39(6): 76-81.
CHEN K, FANG X. Investigation of vehicle road noise transfer path based on operational transfer path analysis[J]. Journal of Shenyang Ligong University, 2020, 39(6): 76-81.
Transfer path analysis of product packaging system under random vibration
CHEN Jun-fei 1,2,3 ?ZHANG Yuan-biao 1,2,3 ?LIN Cong 1,2,3
1. Packaging Engineering Institute, Jinan University, Zhuhai 519070, China;
2. Key Laboratory of Product Packaging and Logistics of Guangdong Higher Education Institutes, Jinan University, Zhuhai 519070, China;
3. Zhuhai Key Laboratory of Product Packaging and Logistics, Jinan University, Zhuhai 519070, China
Abstract The vibration response of the product packaging system under different excitation spectra, different vibration levels, different cushion thicknesses and different cushion distribution methods are investigated, and the vibration contribution of each transfer path of the product packaging system under random vibration is quantified by using the OTPA method. The results show that when the vibration level is high, the packaging system show slight jumping phenomenon, and the vibration response of the system increases while the resonance frequency decreases slightly. With the increase of the cushion thickness, the resonance frequency of the system decreases, the acceleration response power spectrum (PSD) of the critical element under different excitation spectra is different, the vibration response is related to the excitation energy at the resonance frequency of the system, and the cushion thickness has a small effect on the vibration contribution of each path. When the cushion pad area is uniformly distributed, the OTPA method is used to identify the main vibration contribution path of the system, which is defined as the critical vibration transfer path, and the response of the critical element is closely related to the vibration contribution of the critical vibration transfer path near the resonant frequency, and the design of the cushion package should focus on the vibration damping design of the critical vibration transfer path. The results of the study provide theoretical support for further research on cushion packaging design methods.
Keywords random vibration; packaging system; PSD; OTPA; vibration contribution

