随机车载激励的斜拉索非线性振动响应极值预测

赵辉 陈水生 李锦华 任永明

摘要 为了预测随机车辆荷载作用下斜拉索非线性振动的响应极值，采用蒙特卡罗随机抽样法生成随机车流荷载，求解随机车流荷载在斜拉索梁端和塔端产生的位移；将索端车致位移作为斜拉索的外部激励输入，采用龙格?库塔数值方法求解斜拉索的非线性空间耦合振动响应；基于经典Rice公式极值预测理论，提出随机车载激励的斜拉索非线性振动响应极值预测方法。实际工程的应用结果表明：车辆荷载为斜拉索的梁端提供了较大的竖向和纵向位移激励，为塔端提供了较大的纵向位移激励，其对拉索的轴向和面内振动响应影响较大，对拉索的面外振动响应影响较小；斜拉索的车致振动响应极值随着车流密度和重现期的增大而增大；经典Rice公式对斜拉索车致振动响应界限跨阈次数的拟合效果很好，提出的斜拉索非线性振动响应极值预测方法有效可靠且在工程实践中应用方便。

关键词 极值预测; 斜拉索; 非线性振动; 随机车载; 经典Rice公式

引 言

随着中国综合国力和桥梁建造技术的提高，大跨度斜拉桥因其造型美观和跨越能力较大而在公路交通中迅速发展。但斜拉桥本身属于柔性结构，其最为关键的受力构件斜拉索，在外部荷载激励下会产生不同程度的非线性振动响应［1?4］，斜拉索的使用寿命和运营安全备受关注。过桥车辆荷载每时每刻都会在斜拉桥上出现，在某些时段甚至是密集出现，具有较大的波动性和高度的随机性，是斜拉索产生振动的主要激励源。因此，研究斜拉索在车辆荷载激励下的振动响应显得非常必要，也很有实际意义。

针对移动车辆荷载激励的斜拉索振动问题，学者们已经从两个方面开展了相关的研究：（1）车辆荷载激励的斜拉索线性振动，如：XIE等［5］对比分析了二轴汽车作用下的CFRP斜拉索和钢斜拉索的車致振动响应；ZHANG等［6］基于LS?DYNA显式动力分析软件，分析了公铁两用斜拉桥斜拉索在列车荷载作用下的振动响应；MU等［7］采用改进的抛物线索单元，分析了列车行车速度和轨道不平顺对拉索动张力的影响；SUN等［8］从静力和动力两个方面对比分析了车辆荷载作用的钢索斜拉桥、CFRP索斜拉桥、钢索+CFRP索斜拉桥的拉索振动响应；李永乐等［9］建立大跨度铁路斜拉桥的有限元模型，采用瞬态分析方法讨论了不同方向索端位移激励下斜拉索线性振动响应。（2）车辆荷载激励的斜拉索非线性振动，如：杨孚衡等［10］在研究铁路斜拉桥在高速列车荷载作用下的振动响应时指出，斜拉索的振动应该考虑其非线性的影响；ZHU等［11?12］在非线性范围内对铁路斜拉桥在重载列车荷载作用下的斜拉索振动响应进行研究；SONG等［13］分析移动独轮车过桥时的斜拉索非线性振动响应；张鹤等［14］基于车桥耦合振动理论，将二轴汽车简化为半车模型，研究公路斜拉桥斜拉索在汽车荷载作用下的非线性振动响应；ZHOU等［15］综合考虑风荷载和车辆荷载的共同作用，对比分析等效静力法和非线性动力法的索力值。

可以看出，上述学者对斜拉索的车致振动研究做了很多工作。但是，有关该领域的研究还需要继续完善：（1）有关公路斜拉桥斜拉索的车致振动研究有待进一步探索，特别是随机车流荷载激励的斜拉索非线性空间耦合振动研究还是空白。（2）在大宗货物运输不断增加和汽车工业飞速发展的情况下，为了保证大跨度斜拉桥的运营安全，桥梁建设者和管养单位越来越关注斜拉索在未来服役时间内可能出现的极端振动响应。那么，如何得到在役斜拉索在随机车辆荷载作用下的振动响应极值就显得至关重要。鉴于此，本文基于经典Rice公式极值预测理论，综合考虑过桥车辆的随机性和斜拉索空间耦合振动的非线性，提出公路斜拉桥斜拉索的车致振动响应极值预测方法。为类似桥梁的建造、管养、安全评估和修复加固提供科学的事前决策依据。

1 索端位移激励的斜拉索非线性振动响应求解

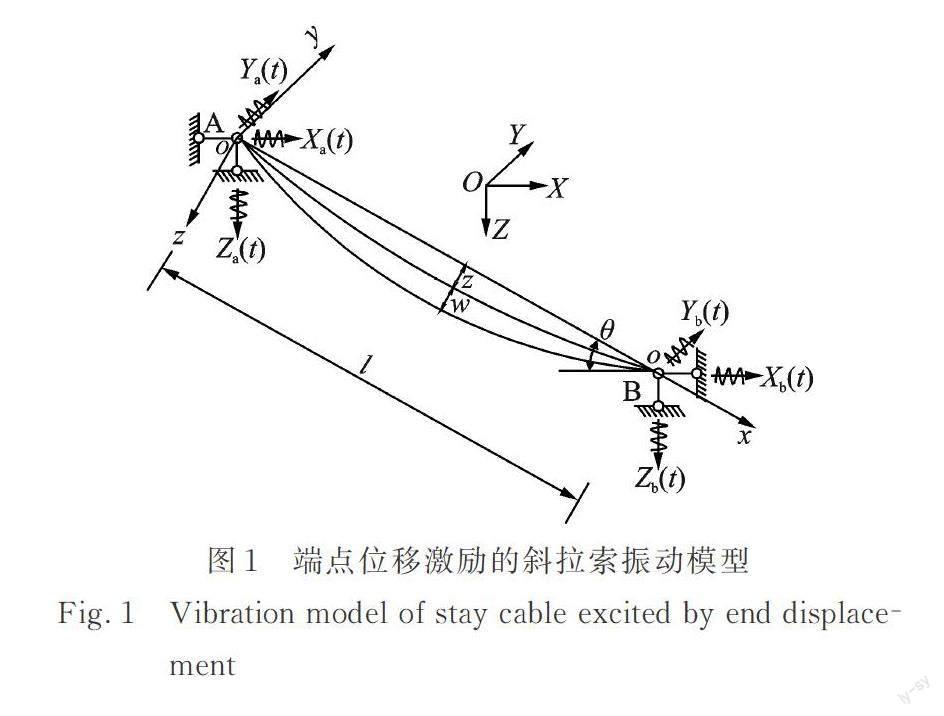
为了求解斜拉索的非线性空间耦合振动响应，在此采用图1端点位移激励的斜拉索振动响应计算模型，并做如下的基本假设：①斜拉索材料为线弹性，变形满足胡克定律；②忽略拉索的抗扭刚度和抗剪刚度；③考虑拉索的几何非线性、抗弯刚度和轴向惯性力；④斜拉索的初始静态线形为抛物线。

在图1中，整体坐标用X?Y?Z描述，斜拉索局部振动用x?y?z局部坐标描述，xoz面为面内，xoy面为面外。斜拉索长度为l，A端为索塔连接处，B端为索梁连接处。考虑斜拉索的垂度和抗弯刚度，可得随机车载激励的斜拉索非线性空间耦合振动方程［16］。根据斜拉索空间振动方程的边界条件［17］，采用Galerkin方法进行模态截断，可以推得斜拉索的振动响应表达式：

式中 Xa（t），Xb（t），Ya（t），Yb（t），Za（t），Zb（t）为桥塔、主梁与斜拉索连接点的车致位移；Un（t），Vn（t）和Wn（t）分别为斜拉索轴向、面外和面内的模态广义坐标［16］；φu，n（x），φv，n（x），φw，n（x）为斜拉索在各个方向的振型函数。

根据Tagata［18］的研究结果，对于端部激励下的张紧弦振动，其一阶模态占主导地位，故斜拉索的振动响应分析取一阶模态可以满足实际工程精度要求［19］。但本文为了考虑斜拉索多阶模态的耦合效应，取前十阶模态进行斜拉索振动响应的求解。

2 斜拉索车致非线性振动响应的极值预测方法

2.1 经典Rice公式极值预测理论

已有的研究表明，如果桥梁的车致荷载效应假定为平稳高斯随机过程［20］，则斜拉索车致振动响应与给定界限的交叉次数就可以采用经典Rice公式［21］来拟合。若x为斜拉索的车致非线性振动响应随机过程，则单位时间内x的跨阈率v（x）可以表示为：

式中 m，σ和σ˙分别为随机变量x的均值、标准差和x导数的标准差。

将式（4）两边取对数，经整理可得：

采用最小二乘法对跨阈率v（x）的高尾部分进行拟合，并对拟合结果进行K?S检验，以选择最优的拟合起点和界限区间值。那么，R重现期的斜拉索车致振动响应极值xmax（R）可以表示为：

式中 vopt，mopt和σopt分别为经典Rice公式的均值点跨阈率、均值和标准差的最优拟合参数。

随机过程x在桥梁服役期T内的极值概率分布函数和概率密度函数分别为：

根据高速公路桥梁的车流数据特征，过桥车流状态与车流密度密切相关，其体现了行车间距的大小和人类作息时间的变化。然而，中国各地区的经济发展速度、公路交通车流量及车流中车型的组成存在较大差异，有关车流运行状态的划分还没有明确的界限。因此，本文在考虑车流状态对斜拉索车致振动响应的影响时，参考已有的研究［22］，以车流密度200和400 veh/h作为划分界限，将日过桥车流划分为稀疏（车流密度<200 veh/h）、一般（200 veh/h<车流密度<400 veh/h）和密集（车流密度>400 veh/h）三种状态。那么，根据跨阈率叠加原理，可以将不同车流状态的斜拉索车致振动响应界限跨阈率进行叠加，得到实际车流的斜拉索车致振动响应界限跨阈率：

式中 vx（x），vy（x）和vm（x）分别为稀疏、一般和密集车流的斜拉索车致振动响应界限跨阈率；px，py，pm为不同车流状态的占比。

将式（9）代入式（4），拟合经典Rice公式的最优待定参数，进而得到实际车流荷载作用的斜拉索振动响应极值的概率分布，并预测斜拉索在未来服役时间的车致振动响应极值。

2.2 斜拉索车致振动响应的极值预测流程

斜拉索车致非线性振动响应极值预测主要分为四大部分：随机车辆荷载的模拟、斜拉索梁端和塔端车致位移的求解、索端位移激励的斜拉索非线性振动响应求解、斜拉索非线性振动响应极值预测模型的建立，其主要计算步骤如下：

（1）根据过桥车辆的車辆类型、车辆行驶车道、车辆载重量、车辆行驶间距和车辆行驶状态统计参数，采用蒙特卡罗随机抽样的方法生成满足实际交通状况的随机车流荷载。

（2）采用ANSYS软件建立斜拉桥的有限元模型，得到单位荷载作用的桥梁任意位置的位移影响面。将随机车流中各车辆的车轮荷载等效为集中力，利用影响面加载的方法计算随机车流荷载作用的斜拉索梁端和塔端X，Y和Z方向的位移。

（3）将斜拉索塔端和梁端的车致位移作为斜拉索非线性振动的外部激励源，代入公式（1）～（3），采用龙格?库塔数值方法求解斜拉索的轴向、面内和面外振动响应。

（4）根据1000天的斜拉索车致非线性振动响应样本，建立不同车流状态的界限跨阈率模型并进行跨阈率叠加；采用最小二乘法和K?S检验法拟合经典Rice公式的最优参数，建立斜拉索车致非线性振动响应极值的预测模型，进而预测斜拉索车致非线性振动响应的极值。

随机车载激励的斜拉索非线性振动响应的极值预测流程图如图2所示。

3 工程应用

以鄱阳湖二桥为工程背景，该桥跨越有中国内陆“百慕大”之称的鄱阳湖老爷庙水域，为五跨双塔空间双索面钢?混凝土组合梁斜拉桥。主桥各跨径为：68.6 m+116.4 m+420 m+116.4 m+68.6 m，72对斜拉索呈双索面扇形布置，拉索最大长度为223.042 m（编号：Z18），拉索最小长度为60.168 m（编号：Z1）。设计荷载为公路?Ⅰ级，双向四车道，设计车速为100 km/h，桥面宽度为24.5 m。因桥梁为完全对称结构，半桥布置图如图3所示，图中各拉索分别编号。

3.1 随机车载模拟

3.1.1 车型及车道

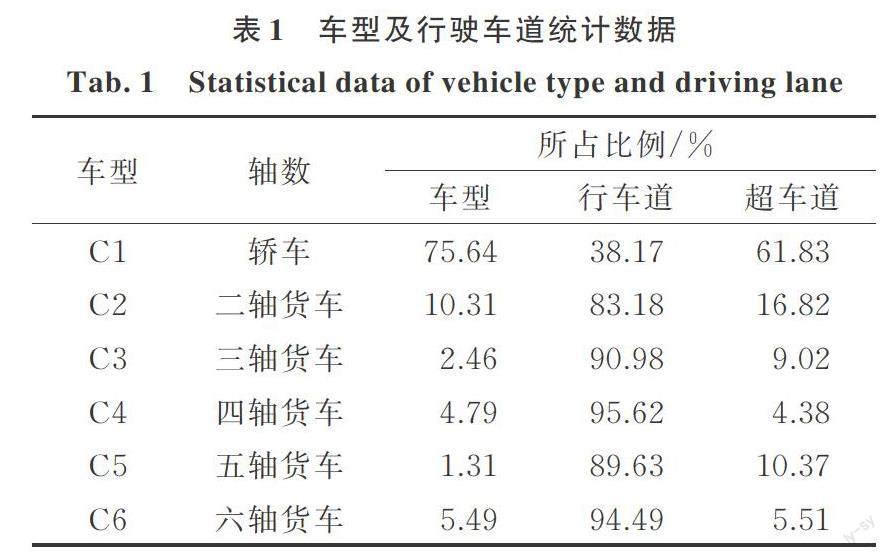
高速公路上行驶车辆的类型较多，根据现场调查结果并参考已有的研究［23］，可以将车辆分为六种代表性车型，各车型及其行驶车道的统计数据如表1所示，各车型出现的频率和车辆车道的选择可以采用均匀分布函数来生成［24］。

3.1.2 车 重

通常情况下，行驶车辆的载重可以分为空载、一般载重和重载三种情况，车重的最小值是空载情况下车辆自身的重量，车重的最大值与车辆的超载有关。根据实际交通监测数据，各车型的车重统计结果呈现出多峰分布的特点，可以采用混合正态分布拟合各车型的车重［25］，拟合的混合正态分布参数如表2所示，表中μi和σi分别为第i个正态分布的均值和标准差。以C6车型为例，图4给出了其车重的直方图和混合正态分布的概率密度拟合结果，可以看出，车重具有明显的多峰分布特征。

3.1.3 车 距

根据实际交通状况，稀疏、一般和密集车流的占比分别约为0.474，0.329和0.197，单向日通行量分别约为2988，2400和1020辆。稀疏和一般车流的车辆间距可以采用对数正态分布生成车距样本，密集车流的车辆间距可以采用伽马分布生成车距样本［26］，其分布参数分别为（7.21，0.42），（6.52，0.68）和（6.43，9.15）。根据不同车流的车辆间距样本拟合的概率密度曲线如图5所示，从图中可以看出，随着车流密度的增大，车辆间距的均值减小，概率密度曲线的峰值越来越大，车距样本的离散性越来越小。

以一般车流为例，综合考虑车型、车道、车重和车辆间距的随机性特征，采用蒙特卡罗随机抽样的方法生成某一时段的车流样本如图6所示。

3.2 索端位移激励的求解

过桥随机车流中的车辆数量很多，如果所有车辆都采用整车模型，计算时间将很长。为简化计算，按照文献［27］的车辆轴重分配比例将各车轮荷载简化为一个集中力，采用影响面加载的方法计算斜拉索塔端和梁端的车致位移。以最长斜拉索Z18为研究对象，当单位集中荷载在桥面上移动时，斜拉索梁端Z方向和塔端X方向的位移影响面如图7所示。

在一般车流荷载作用下，斜拉索Z18梁端和塔端的位移时程曲线如图8所示。从图8中可以看出，斜拉桥车致位移的随机性很强，任意一个峰值点的出现都说明有一辆重型货车过桥；梁端竖向位移大于纵向位移，而横向位移最小；塔端纵向位移大于横向位移，而竖向位移最小，且塔端位移小于梁端位移。可见，随机车流荷载给斜拉索的梁端提供了较大的竖向和纵向位移激励，也给斜拉索的塔端提供了较大的纵向位移激励。

同时，为了探究过桥随机车流的荷载效应是否具有平稳高斯随机过程的特征，以斜拉索Z18梁端Z方向的车致位移为例，图9给出了该随机过程的均方差随时间的变化曲线，图10给出了该随机过程的频数直方图及其拟合的正态分布概率密度曲线。从图9中可以看出，Z18梁端Z方向车致位移的均方差随着时间的增加而趋于稳定，即随机车辆荷载效应样本数量较大时，该随机过程呈现出平稳随机过程的特征；从图10中可以看出，正态分布概率密度曲线对Z18梁端Z方向车致位移频数直方图的拟合效果很好，即该随机过程具有高斯随机过程的特征。

3.3 索端激励的斜拉索非线性振动响应求解

当一辆载重量为44.5 t的六轴货车过桥时，图11给出了单车荷载激励的最长斜拉索Z18中点的线性和非线性振动响应。从图11中可以看出，拉索面内振动响应最大，轴向振动响应次之，而面外振动响应最小；拉索非线性空间耦合振动响应大于线性振动响应，前者的轴向、面外、面内振动响应最大值分别是后者的1.41倍、1.3倍、2.81倍。因此，研究公路斜拉桥斜拉索的车致振动响应，很有必要考虑拉索的非线性和拉索不同方向振动的空间耦合关系。

在车辆荷载作用下，为了分析索端车致位移激励对斜拉索非线性空间耦合振动响应的影响，在此考虑五种索端位移激励工况：工况1，索端纵向位移激励，即Xa（t）和Xb（t）；工况2，索端竖向位移激励，即Ya（t）和Yb（t）；工况3，索端横向位移激励，即Za（t）和Zb（t）；工况4，工况1+工况2共同作用；工况5，工况1+工况2+工况3共同作用。

在不同的索端位移激励工况下，斜拉索Z18中点的非线性空间耦合振动响应如图12所示。从图12中可以看出：（1）工况4和工况5的拉索轴向和面内振动响应相同，工况3和工况5的拉索面外振动响应相同，说明索端横向位移激励对拉索轴向和面内的振动响应影响很小，但对拉索面外振动响应的影响较大。（2）索端竖向位移激励对拉索面内和轴向振动响应的影响大于索端纵向位移激励对拉索面内和轴向振动响应的影响；索端纵向和竖向位移激励对拉索的面外振动响应影响较小。（3）工况4和工况5的拉索面内振动响应小于工况2的拉索面内振动响应，说明索端纵向和竖向位移的联合激励导致拉索面内振动响应有所减小；工况4和工况5的拉索轴向振动响应大于工况1和工况2的拉索轴向振动响应，说明索端纵向和竖向位移的联合激励增大了拉索轴向振动响应。

当考虑过桥车辆的随机性时，斜拉索Z18在一般车流荷载作用下的中点非线性空间耦合振动响应如图13所示。从图13中可以看出，斜拉索非线性振动响应随机性很强，振动响应值的大小与索端位移激励的大小有很大关系。斜拉索非线性振动响应主要以面内和轴向振动响应为主，而面外振动响应相对较小；在该时段，面内振动响应的最大值为105 mm，轴向振动响应的最大值为27.8 mm，面外振动响应的最大值为1.8 mm。

那么，根据斜拉索的轴向振动响应可得随机车辆荷载作用的斜拉索应力，不同的车流状态和车流占比，斜拉索Z18在某一天内的应力时程如图14所示。从图14中可以看出，密集车流的拉索应力最大，一般车流的拉索应力次之，稀疏车流的拉索应力最小；在该天的应力时程样本中，密集车流的拉索应力最大值为40 MPa，一般车流的拉索应力最大值为28.8 MPa，稀疏车流的拉索应力最大值为25.2 MPa。

3.4 斜拉索振动响应的界限跨阈率拟合

如果每年按250个有效日历天来计算，基于斜拉索的车致振动响应模拟数据，用1000天的斜拉索车致振动响应样本来拟合经典Rice公式。图15给出了不同的过桥车流状态，斜拉索Z18中点的车致振动响应界限跨阈率曲线拟合结果。从图15中可以看出，经典Rice公式对斜拉索车致振动响应年跨阈次数的拟合效果很好，实际车流荷载作用的斜拉索振动响应年跨阈率曲线是稀疏、一般、密集车流荷载作用的斜拉索振动响应年跨阈率叠加的结果。斜拉索Z18中点的车致位移和车致应力的vopt，mopt，σopt最优拟合结果分别如表3和4所示，由表中数据可知，不同的车流状态，斜拉索车致振动响应的均值和标准差随着过桥车流密度的增大而增大。

3.5 斜拉索车致振动响应的极值预测

根据公式（6）预测的斜拉索Z18中点的车致振动响应极值如图16所示。从图16中可以看出，斜拉索的轴向、面外、面内振动响应极值随着重现期的增大而增大；密集车流荷载作用的拉索振动响应极值最大，稀疏车流荷载作用的拉索振动响应极值最小，而综合考虑各车流占比的实际车流荷载作用的拉索振动响应极值与密集车流荷载作用的拉索振动响应极值接近；虽然密集车流的占比最小，但其控制了斜拉索振动响应极值的大小。鄱阳湖二桥于2019年建成通车，已服役2年，按照目前的过桥车流状态，斜拉索Z18在剩余设计使用年限18年重现期的轴向、面外、面内振动响应极值分别为59.03，3.276，176.6 mm。

图17给出了斜拉索Z18在桥梁设计基准期100年内的车致振动响应极值的概率密度函数（PDF）和累积分布函数（CDF）。文献［28］对车辆荷载效应的重现期定义为设计基准期内具有95%保证率的最大值。从图17中可以看出，斜拉索轴向、面外、面内车致位移极值的期望分别为62.8，3.5，184.39 mm，95%保证率的位移极值分别为68.6，3.9，198.8 mm。

不同的车流状态，斜拉索Z18在不同重现期的车致应力极值如图18所示。从图18中可以看出，斜拉索的车致应力极值随着重现期的增大而增大；密集车流荷载作用的拉索应力极值最大，稀疏车流荷载作用的拉索应力极值最小，而实际车流荷载作用的拉索应力极值仅次于密集车流作用的拉索應力极值。按照目前的过桥车流状态，斜拉索Z18在剩余设计使用年限18年重现期的应力极值为51.69 MPa。

同时，图19给出了斜拉索Z18在设计基准期100年内的车致应力极值的PDF和CDF。从图19中可以看出，随机车辆荷载激励的斜拉索应力极值的期望为55 MPa，95%保证率的应力极值为60.4 MPa。

4 結 论

（1）在过桥车辆荷载作用下：公路斜拉桥斜拉索的梁端产生了较大的竖向和纵向位移，塔端产生了较大的纵向位移；斜拉索的轴向和面内振动响应取决于索端纵向和竖向位移激励，受索端横向位移激励的影响很小；斜拉索的面外振动响应取决于索端横向位移激励，受索端纵向和竖向位移激励的影响很小；斜拉索的非线性振动响应大于线性振动响应，且斜拉索的面内振动响应最大，轴向振动响应次之，而面外振动响应最小。

（2）经典Rice公式对斜拉索车致振动响应界限跨阈次数的拟合效果很好，可以保证斜拉索车致振动响应极值预测模型的可靠性。斜拉索的车致振动响应极值受过桥车流密度的影响较大，其随着车流密度的增大而增大；在未来服役时间内，斜拉索的车致振动响应极值随着重现期的增加而增大。

（3）提出的随机车载激励的斜拉索非线性振动响应极值预测方法是在经典Rice公式极值预测理论的基础上，通过严谨的数学推导而得到的；其有效解决了公路斜拉桥斜拉索的车致振动响应极值预测问题，可为新建斜拉桥和在役斜拉桥的斜拉索安全评估、修复加固和剩余寿命预测提供有效的事前决策数据。

（4）有关风、雨、随机车流联合激励的斜拉索振动响应极值预测，有关考虑斜拉索抗力退化时变性及外部激励荷载非平稳性的斜拉索振动响应极值预测等研究工作有待进一步探索，将更有挑战性和现实意义。

参考文献

1KANG H J， ZHU H P， ZHAO Y Y， et al. In-plane nonlinear dynamics of the stay cables［J］. Nonlinear Dynamics， 2013， 73（3）： 1385-1398.

2YI J， LI J Z. Modelling of stay cables with large earthquake-induced force variations in cable-stayed bridges［J］. Structures， 2021， 33： 627-636.

3LI S Y， WANG Y Y， ZENG Q Y， et al. Coupled responses of stay cables under the combined rain-wind and support excitations by theoretical analyses［J］. Advances in Structural Engineering， 2020， 23（11）： 2261-2275.

4CONG Y Y， KANG H J， GUO T D. Analysis of in-plane 1∶1∶1 internal resonance of a double cable-stayed shallow arch model with cables external excitations［J］. Applied Mathematics and Mechanics （English Edition）， 2019， 40（7）： 977-1000.

5XIE X， LI X Z， SHEN Y G. Static and dynamic characteristics of a long-span cable-stayed bridge with CFRP cables［J］. Materials， 2014， 7： 4854-4877.

6ZHANG X Y，JIN X L，CHEN X D. Simulation of the interactions between a train and a long-span cable-stayed bridge using parallel computing with domain decomposition［J］. Proceedings of the Institution of Mechanical Engineers， Part F： Journal of Rail and Rapid Transit， 2012， 226（4）： 347-359.

7MU D，GWON S G，CHOI D H. Dynamic responses of a cable-stayed bridge under a high speed train with random track irregularities and a vertical seismic load［J］. International Journal of Steel Structures， 2016， 16（4）： 1339-1354.

8SUN S J， MEI K H， SUN Y M， et al. Structural performance of super-long-span cable-stayed bridges with steel and CFRP hybrid cables［J］. Arabian Journal for Science and Engineering， 2020， 45（5）： 3569-3579.

9李永乐， 孙超， 向活跃， 等. 三维随机激励作用下斜拉索参数振动的有限元分析［J］. 桥梁建设， 2017， 47（2）： 19-24.

LI Yongle， SUN Chao， XIANG Huoyue， et al. Finite element analysis of parametric vibration of stayed cable under three-dimensional random excitation［J］. Bridge Construction， 2017， 47（2）： 19-24.

10杨孚衡， 黎志光. 考虑斜拉桥非线性的车桥耦合振动分析［J］. 中国铁道科学， 2001， 22（3）： 67-71.

YANG Fuheng， LI Zhiguang. Dynamic response of cable-stayed bridge under moving forces with consideration of nonlinearity of stay-cables［J］. China Railway Science， 2001， 22（3）： 67-71.

11ZHU Z H， WANG L D， DAVIDSON M T， et al. Nonlinear dynamic analysis of long-span cable-stayed bridges with train-bridge and cable coupling［J］. International Journal of Advanced Structural Engineering， 2019， 11： 271-283.

12朱志輝， 刘宇， 龚威， 等. 重载列车引起的大跨度斜拉桥拉索振动研究［J］. 振动工程学报， 2020， 33（1）： 149-157.

ZHU Zhihui， LIU Yu， GONG Wei， et al. Analysis of cable vibration of long-span cable-stayed bridge induced by heavy haul train［J］. Journal of Vibration Engineering， 2020， 33（1）： 149-157.

13SONG M T， CAO D Q， ZHU W D， et al. Dynamic response of a cable-stayed bridge subjected to a moving vehicle load［J］. Acta Mechanica， 2016， 227（10）： 2925-2945.

14张鹤， 谢旭. 车辆荷载作用下大跨度斜拉桥钢和CFRP拉索的非线性振动［J］. 工程力学， 2009， 26（8）： 123-130.

ZHANG He， XIE Xu. Nonlinear vibration of steel and CFRP cables of long span cable-stayed bridge under vehicular loads［J］. Engineering Mechanics， 2009， 26（8）： 123-130.

15ZHOU Y F， CHEN S R. Numerical investigation of cable breakage events on long-span cable-stayed bridges under stochastic traffic and wind［J］. Engineering Structures， 2015， 105： 299-315.

16雷大根， 郑久建， 刘晓丰， 等. 端部激励下斜拉索三维振动统一方程的精细推导［J］. 中国公路学报， 2019， 32（8）： 92-100.

LEI Dagen， ZHENG Jiujian， LIU Xiaofeng， et al. Fine derivation of the unified equation for three-dimensional vibration of stayed cable under end excitation［J］. China Journal of Highway and Transport， 2019， 32（8）： 92-100.

17孙测世， 彭剑， 赵珧冰， 等. 斜拉桥主梁纵向漂移对拉索非线性振动影响［J］. 工程力学， 2014， 31（11）： 86-91.

SUN Ceshi， PENG Jian， ZHAO Yaobing， et al. Effect of longitudinal floating of girder on nonlinear vibrations of stay cables［J］. Engineering Mechanics， 2014， 31（11）： 86-91.

18TAGATA G. Harmonically forced， finite amplitude vibration of a string［J］. Journal of Sound and Vibration， 1977， 51（4）： 483-492.

19陈水生， 孙炳楠. 斜拉桥索-桥耦合非线性参数振动数值研究［J］. 土木工程学报， 2003， 36（4）： 70-75.

CHEN Shuisheng， SUN Bingnan. Numerical study on nonlinear parametric vibration of coupled cables and bridge decks［J］. China Civil Engineering Journal， 2003， 36（4）： 70-75.

20LEAHY C， OBRIEN E， OCONNOR A. The effect of traffic growth on characteristic bridge load effects［J］. Transportation Research Procedia， 2016， 14： 3990-3999.

21CREMONA C. Optimal extrapolation of traffic load effects［J］. Structural Safety， 2001， 23（1）： 31-46.

22魯乃唯， 刘扬， 肖新辉. 实测车流作用下大跨桥梁荷载效应极值外推法［J］. 交通运输工程学报， 2018， 18（5）： 47-55.

LU Naiwei， LIU Yang， XIAO Xinhui. Extrapolating method of extreme load effects on long-span bridge under actual traffic loads［J］. Journal of Traffic and Transportation Engineering， 2018， 18（5）： 47-55.

23BAILEY S F， Bez R. Site specific probability distribution of extreme traffic action effects［J］. Probabilistic Engineering Mechanics， 1999， 14： 19-26.

24刘扬， 张海萍， 鲁乃唯， 等. 基于WIM的随机车流建模和简支梁桥荷载效应研究［J］. 桥梁建设， 2015， 45（5）： 13-18.

LIU Yang， ZHANG Haiping， LU Naiwei， et al. Study of random vehicle flow modeling and load effect of simply-supported beam bridge based on WIM data［J］. Bridge Construction， 2015， 45（5）： 13-18.

25CHEN W Z， Ma C， XIE Z L， et al. Improvement of extrapolation of traffic load effect on highway bridges based on Rices theory［J］. International Journal of Steel Structures， 2015， 15（3）： 527-539.

26OBRIEN E J， CAPRANI C. Headway modelling for traffic load assessment of short to medium span bridges［J］. Structural Engineer， 2005， 83（16）： 33-36.

27张喜刚. 公路桥梁汽车荷载标准研究［M］. 北京： 人民交通出版社， 2014.

ZHANG Xigang. Study on Automobile Load Standard of Highway Bridge［M］. Beijing： China Communications Press， 2014.

28中交公路规划设计院有限公司. 公路工程结构可靠性设计统一标准： JTG 2120―2020［S］. 北京： 人民交通出版社， 2020.

Zhongjiao Highway Planning and Design Institute Co.， Ltd.. Unified standard for reliability design of highway engineering structures： JTG 2120―2020［S］. Beijing： China Communications Press， 2020.

Extreme prediction of nonlinear vibration response of stay cable under random vehicle excitation

ZHAO Hui 1 ?CHEN Shui-sheng 2LI Jin-hua 2REN Yong-ming 2

1. College of Architecture and Civil Engineering， Xinyang Normal University， Xinyang 464000， China；

2. School of Civil Engineering and Architecture， East China Jiaotong University， Nanchang 330013， China

Abstract In order to predict the extreme value of nonlinear vibration response of stay cable under random vehicle load. Firstly， Monte-Carlo random sampling method is used to generate random traffic flow load， and the displacement of stay cable beam end and tower end under random traffic flow load is solved. Then， the vehicle induced displacement at the beam end and tower end of the stay cable is taken as the external excitation input of the stay cable， and the nonlinear spatial coupling vibration response of the stay cable is solved by Runge-Kutta numerical method. Finally， based on the extreme value prediction theory of classical rice formula， an extreme value prediction method of nonlinear vibration response of stay cable under random vehicle excitation is proposed. The practical engineering application results show that the vehicle load provides a large vertical and longitudinal displacement excitation for the beam end of the cable， and a large longitudinal displacement excitation for the tower end， which has a great influence on the axial and in-plane vibration response of the cable， and a small influence on the out-of-plane vibration response of the cable. The extremum of vehicle-induced vibration response of stay cable increases with the increase of traffic density and recurrence period. The classical Rice formula has a good fitting effect on the threshold crossing times of vehicle-induced vibration response limit of stay cable. The prediction method of extreme value of nonlinear vibration response of stay cable proposed in this paper is effective， reliable and convenient to be applied in engineering practice.

Keywords extreme value prediction; stay cable; nonlinear vibration; random traffic load; classical Rice formula