岱山大坝渗流预测模型研究及渗漏问题分析

窦 飞，薛江寒

（1.安徽水安建设集团股份有限公司，安徽 合肥 230601；2.华北水利水电大学水利学院，河南 郑州 450046）

土石坝是历史上最为悠久且建设过程中应用最为广泛的一种坝型，其凭借着地基适应能力强、经济性好、就地取材等特点在坝工界占有十分重要的地位[1]。据不完全统计，我国现有水库大坝共9.8万余座，其中95%以上为土石坝[2]。在全世界所建造的百米级高坝中，土石坝所占比重也在逐年增长，从20 世纪50 年代以前的30%增至20 世纪80 年代的70%以上。由渗流问题引发的大坝安全事故占据大坝失事的40%以上，因此渗流安全就是保证石坝安全运行的重要条件之一。现如今，我国的土石坝大多为中、小型水库，其受历史条件、设计水平、施工及运行管理等因素影响，已成为需除险加固的“病害”水库。其中，绝大多数水库蓄水运行之后，均质土坝的坝体、坝肩及坝基会出现不同程度的渗漏问题，若大坝的防渗措施布置不到位或监测设施损坏，则渗透压力会导致坝体发生渗流破坏；同时，坝体浸润线以下的土体也会因含有饱和水而降低抗剪强度指标，从而导致坝体发生滑坡破坏[3]。

国内大坝建设水平世界领先，但管理水平相对滞后，智能诊断与协调管理能力相对薄弱[2]。为保证大坝运行期间的安全稳定性，需水库管理人员现场检查并结合监测资料对土石坝渗流情况进行控制。渗流预测的目的就是为防渗布置设计、选择合理的渗控方案提供技术依据，保障大坝各部位的渗流稳定性，防止发生管涌、流土等渗流破坏。但由于监测设施年久失修、人为疏忽等不可控因素，更凸显了一个精确且合理的渗流预测模型的重要性。目前，机器学习已在渗流预测领域发挥着十分重要的作用，在已有的土石坝渗流安全预测模型中，吴云星等[4]采用了收敛速度更快、拟合和预测精度更高的改进LMBP 神经网络对土石坝渗流压力进行预测，证明了LMBP 神经网络模型在土石坝压力分析和预测方面是可行的；李瑞光等[5]采用主成分分析法对支持向量回归进行模型优化，建立了均质坝渗流测压管水位的预测模型，可为类似水利工程的坝体监测提供可靠的预测数据；缪长健等[6]利用云模型改进人工鱼群算法（CM-AFSA）的BP 神经网络预测模型，具有高精度和训练效率，在土石坝渗流压力预测和分析方面具有良好的适用性。

但由于中小型水库的监测设施较少，只有测压管水位、库水位2种监测数据，并不像上述研究所示为多因素影响结果。所以，挑选出一种适用于中小型水库渗流预测的模型是十分必要的。时间序列预测一般只需要一组预测变量的历史数据且在短期预测中的效果要比长期预测好，可以完美解决中小型水库中面临监测数据少以及其他影响数据缺失的问题[7]。

本文以岱山水库的实测渗流数据为研究对象，采用3 种经典的机器学习预测方法——BP 神经网络、随机森林RF、支持向量回归SVR模型，通过纳入过去不同时间尺度的输入序列，对考虑库水位、不考虑库水位背景下的测压管水位进行滑动预测。对比不同模型的均方根误差RMSE、均方误差MSE、百分比偏差PBIAS值，从而选择出精度最优、误差最小、鲁棒性最强的预测模型。同时，根据有限元计算及实测资料分析渗漏问题成因，为岱山水库未来分析研究弥补数据信息不足的同时也为后续的工程管理及除险加固提供合理性参考。

1 预测模型原理

神经网络BP是一种误差反向传播神经网络，由输入层、输出层和隐含层三部分组成，三层之间的所有神经元节点都是互相连通的。正向传播是指信号从输入层经隐含层到达输出层，层间非线性激活函数f在此选用Sigmoid 型函数，但当输出预测结果与实际测试结果相差较大时，系统进入误差的反向传播阶段，按照误差梯度下降的方法不断修正隐含层权值、偏置的数值，通过不断修改隐含层中数值进行网络学习，减少输出预测值误差[6]，直至误差符合设置标准时停止。BP 神经网络预测模型，如图1所示。

图1 BP神经网络模型

随机森林RF 是Bagging 算法和Random Sub⁃space 算法的组合，由决策树构成基本单元，通过多棵决策树的组合提高分类精确性的算法。其拥有很好的容错性和鲁棒性，具有操作简单、训练速度快、不易陷入过拟合等特点，成为现今热点的研究预测模型。输入原始样本N后，采用Boostrap抽样从原始样本N中随机且有放回地抽取M个样本集用于构建M棵回归树，每次被抽到的样本数据集M约为原始样本N的2/3。生成决策树时，随机产生每棵树上的节点，每个节点的分割变量分别由随机选取的变量决定，这样就会产生许多决策树，这些决策树就组成了“随机森林”。随机森林模型还基于误差和节点纯度，可对各自变量的重要性进行评估，从而识别出影响变量的关键因素。随机森林的结构，如图2所示。

图2 随机森林模型

支持向量回归SVR预测模型，如图3所示。

图3 支持向量回归模型

支持向量回归SVR 预测模型可以将非线性问题转化、映射到高维空间中的线性回归问题，本质为寻找一个最优的分类面，使得所有训练样本离该最优分类面的误差最小；通过控制模型的3 个参数即惩罚系数C、径向基函数的核函数K(x,xi)=ϕ(x)Tϕ(xi)及不敏感损失系数ε来优化模型，以达到最优的效果。SVR模型的表达式为：

式中：α和b分别为控制着超平面的参数，通过改变α和b决定鲁棒性和准确性的较强回归趋势函数；x和f（x）分别为输入值和预测值。

模型算法的具体研究见文章末尾的参考文献[4-13]。

2 工程基本情况

岱山水库位于安徽省定远县东南部，为塑性混凝土心墙坝，是一座集供水、防洪、灌溉、水产养殖为一体的综合利用的中型水库，坝顶高程53.76 m，坝顶宽度6.70 m。岱山水库于1957 年动工兴建，1958 年基本建成并开始发挥效益。由于工程是在特殊的历史背景下兴建的且兴建时受财力、物力限制，施工质量差，工程存在坝基防渗措施不完善、土坝坝体渗漏并有渗透破坏的可能、溢洪道开裂渗水等主要问题。岱山大坝平面布置，如图4所示。

图4 岱山大坝平面布置

2.1 工程渗漏问题

水库枢纽工程建筑物主要有主坝、副坝、正常溢洪道、副溢洪道、放水涵、安全监测设施。溢洪道堰体及两侧坝体运行历史上均出现渗漏情况，上次除险加固后情况有所缓解。现状溢洪道南侧坝体库水位高于48.50 m时有严重的集中渗漏，近些年渗漏量逐年增大，实测最大值达30 m3/h。

自2010 年起，北放水涵南侧背水坡抗震平台高水位时有大面积潮湿、散浸；2011 年起水库高水位运行时，北涵段背水坡人行梯道与坝脚平台相接处存在渗漏出逸点。2019 年5 月对坝体渗漏处采取应急灌浆处理后，现状仍存在渗漏；渗漏段坝体防渗墙为正常溢洪道南侧原浆砌石刺墙加高段，运行过程中存在很大的安全隐患。水库渗漏现状，如图5所示。

图5 水库渗漏现状

2.2 渗流监测资料分析

目前，岱山水库的测压管水位采用测探钟观测，若在观测中发现管水位有异常变化和受降雨影响时会及时复测、加测，认真分析资料，查明原因。观测使用的测绳每季度校核1次。本文选取接近于坝身集中渗漏点的桩号0+300 断面，此处埋设4 根坝身测压管（分别为Ⅱ-1、Ⅱ-2、Ⅱ-3、Ⅱ-4），断面测压管分布如图6所示。

图6 岱山水库桩号0+300断面测压管分布

选取大坝管理中心2012年1月—2019年1月测压管水位、库水位等实测数据，每个数据点间隔10 d，共355 组数据。库水位与坝身桩号0+300 断面测压管水位随时间的变化曲线，如图7所示。

图7 库水位与测压管水位变化曲线

其中，2013 年Ⅱ-4 测压管水位数值基本大于Ⅱ-3 测压管，经过现场调查和与相关管理人员沟通，得知该年份数据出现异常主要为记录人员在统编观测数据时出现数据汇总错误。

由图6—7可知，库水位仅在2013—2014年处于47 m 较低的水位运行，这是因为当年7、8 月平均气温达到了多年的峰值，库水位相应出现了下降。其余年份库水位并没有较大的落差，均处于48～50 m，且年内汛旱期特征明显。其中，测压管Ⅱ-1 位于防渗墙前，水位接近库水位，部分有高于库水位的现象；同时，测压管Ⅱ-1 水位的变化趋势较大，受库水位影响较为明显，当库水位升高时测压管Ⅱ-1 水位升高，反之降低。测压管Ⅱ-2 水位偶有高于库水位的现象，可能因为降雨通过下游坝壳下渗，影响下游侧水位，导致个别测压管水位异常，不影响数据分析；测压管Ⅱ-2位于防渗墙之后，水位在46～48 m内变化，无明显的突变产生，但变化趋势与测压管Ⅱ-1的变化趋势大致相同；同时，测压管Ⅱ-2 相对于测压管Ⅱ-1，水位平均约降低了1.54 m，经分析得出防渗墙防渗效果一般。测压管Ⅱ-1、Ⅱ-2 水位变化趋势较大，且年内极大极小值差异较大，对各模型的学习能力提出了挑战。测压管Ⅱ-3 位于下游坝坡马道处，水位数值更趋于稳定，基本不受库水位变化趋势的影响，一般约为42 m，无明显的突变发生，非常适合模型的学习。

3 渗流模型预测结果与分析

3.1 模型参数及评价指标介绍

本研究利用Python3.10下的Sklearn机器学习库进行计算，硬件所采用的计算平台为12th Gen Intel（R）Core（TM）i7-12700H CPU@2.70 GHz with 16G RAM。本文采用神经网络BP、随机森林RF、支持向量回归SVR模型进行预测，模型具体参数详见表1。

表1 预测模型参数

本文采用评价指标均方根误差RMSE、均方误差MSE、百分比偏差PBIAS对模型的预测精度进行评价[14]。

均方根误差RMSE是预测值与真实值偏差的平方与数据集m比值的平方根，RMSE值越低表明数据越合适，并且对异常值十分敏感。RMSE的计算公式为：

式中：yi为模型真实值；为模型预测值；m为模型测试集。

均方误差MSE是真实值与预测值之差平方的期望。MSE值越小，表明预测模型在测试集的整体表现越好。MSE的计算公式为：

百分比偏差PBIAS可以体现出实测值与预测值的累计偏差，当模拟预测结果与实测结果趋势贴合良好且数据相差较小时，PBIAS可以更加精确地评估模型测压管水位的效果。PBIAS为正值时表示模型模拟值过低，为负值时表示模型模拟值过高，数值越接近0表示模型预测效果越好。PBIAS的计算公式为：

3.2 预测结果分析

选取测压管Ⅱ-1、Ⅱ-2、Ⅱ-3（测压管Ⅱ-4因淤堵导致数据有误）监测数据与库水位进行模拟分析，以数据前80%为训练集、后20%为测试集。为全面比较各种预测模型，在是否考虑库水位条件下，研究输入时间序列长度对模型性能的影响。在试验中，单个步长时间尺度为10 d，先在测试周期内使用滑动窗口法对1、2、3、4、5、7、9、11 步长内的数据进行预测，再预测出未来1 个步长（10 d 后的测压管水位）的数据[15，16]。

3.2.1 预测结果评价指标分析

挑选测压管Ⅱ-1 的模型训练评价指标，其变化曲线如图8—9所示。

图8为在未考虑库水位的情况下，通过对3种预测模型即BP、RF、SVR 模型输入不同时间预测步长得到的模型评价指标RMSE、MSE、PBIAS变化曲线。其中，BP 模型评价指标较RF、SVR 模型的优秀，其RMSE值为0.08～0.12，处于相对较低的水平；MSE值为0.005～0.014，在模型预测中表现极好，说明预测模型的测压管水位与实际测压管水位相差不大；PBIAS值基本为负值，表示预测值较实际值略高，尤其是预测步长为2～3 时BP 模型的PBIAS值接近于0，说明预测值基本可以代替实测结果。3种模型在输入步长为11 时，评价指标均发生了较大的突变，有了质的提升，即时间预测步长对其结果影响较大。

图9为在考虑库水位的情况下，通过对3种预测模型即BP、RF、SVR 模型输入不同时间预测步长得到的模型评价指标RMSE、MSE、PBIAS变化曲线。由图9 可知，3 种模型在考虑库水位影响下进行预测，同样从评价指标RMSE、MSE、PBIAS值进行分析。其中，BP 模型仍然凭借较强的鲁棒性和优秀的评价指标“胜出”，其RMSE、MSE值在时间预测步长为11 时达到最优，但此刻PBIAS值却不如其他时间预测步长时结果好，这表明其预测性能仍受输入时间序列尺度的影响较大。

图9 考虑库水位影响下预测的评价指标

通过对图8 和图9 进行对比分析发现，BP 模型在考虑库水位影响下的各项评价指标较不考虑库水位影响下低，但库水位影响不明显，这表明坝体测压管水位时间序列的自相关性对其未来变化趋势起着更为重要的作用。经综合分析发现，BP 模型在考虑库水位影响下输入不同时间预测步长，无论是RMSE、MSE还是PBIAS的值都相对其他模型较小，这说明BP模型相对于其他模型具有很好的精度、鲁棒性，更适用于岱山大坝的渗流预测。

同样地，利用3种模型对测压管Ⅱ-2、Ⅱ-3水位分别进行预测，得出评价指标结果详见表2—3。

表2 测压管Ⅱ-2预测模型评价指标

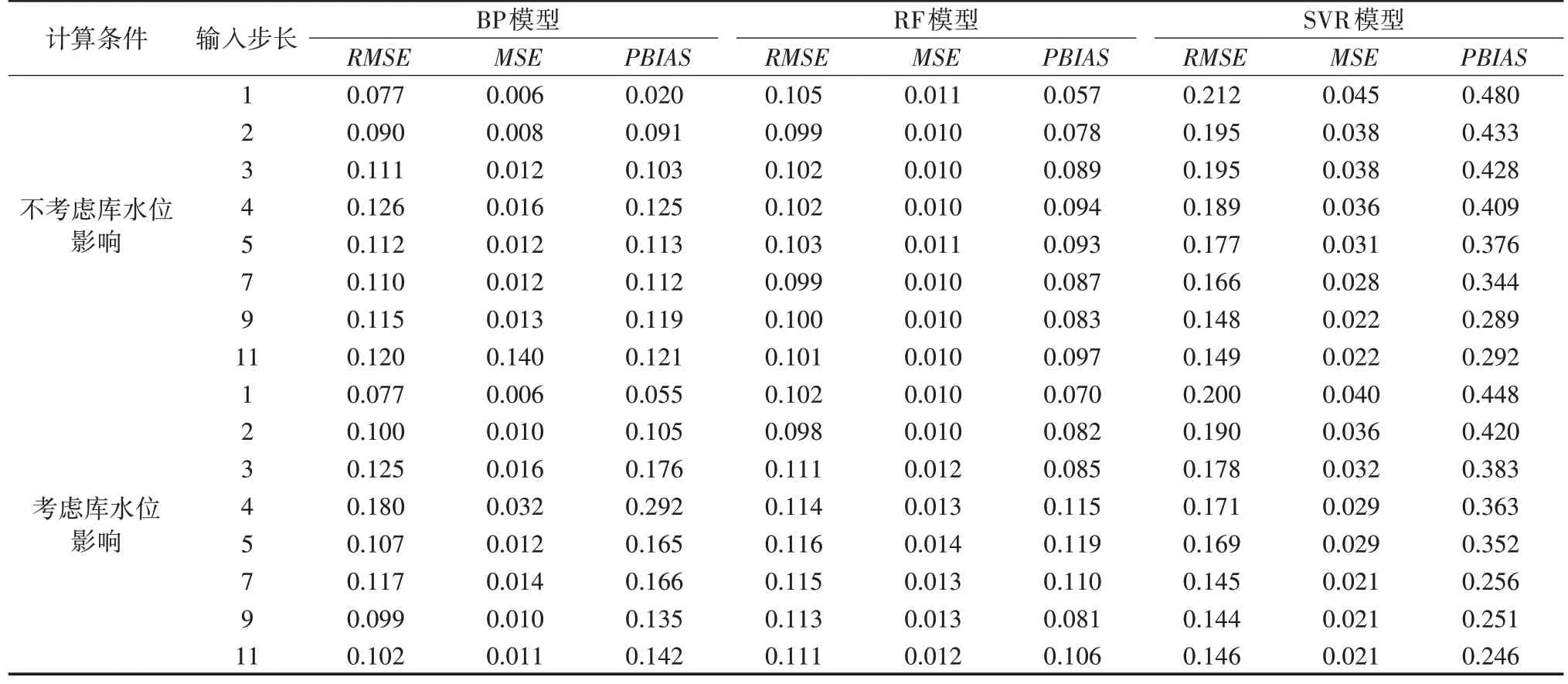
表3 测压管Ⅱ-3预测模型评价指标

由表2—3 可知，测压管Ⅱ-2、Ⅱ-3 预测模型的评价指标仍处于相对较低的水平，且BP模型的预测结果同样优于RF、SVR 模型。但是，测压管水位在是否考虑库水位的条件下，其评价指标相差不大，这是因为测压管Ⅱ-2、Ⅱ-3 均位于防渗墙之后，库水位对其测压管水位的影响较小。

综上可得，BP 模型在考虑库水位影响下输入步长为2～3时（考虑过去20～30 d数据）预测精度最高、效果最好。

3.2.2 测压管水位预测结果及误差分析

选取上述分析出的最优模型即考虑库水位影响下输入步长为3 时的BP 模型的预测值与实测值进行比较，水位预测和实测数据如图10 所示，水位误差分析如图11所示。

图10 测压管水位预测和实测数据对比

图11 测压管水位误差

由图10 可知，模型的预测效果较好，预测值与实测值的变化趋势相同且结果相差不大；由于数据量较小的原因，在预测初期有一个较大的误差点，即出现明显的滞后；而后，经过一段时间的滚动预测后，两者变化趋势开始逐步相似，模型预测对于局部范围内的突变过程表征较为合理，且实测值与预测值几乎相同。同时，由图11 可以看出，仅有一个测压管水位的误差较大，而其他误差均保持在约0.1 m，是一个相对较低的水平。

综上分析，BP 模型较RF、SVR 模型的预测精度更高、鲁棒性更强，在考虑库水位影响下，当输入步长为2～3 时能够很好地模拟出测压管水位的具体数值及其变化趋势，可以对后期水库的监测管理、风险评估提供参考和依据。但由于数据集量级较小的原因，模型会产生较小的误差，后续需要多种优化算法对模型的参数进行选优，同时继续提供监测数据以便模型进行训练。

4 工程渗漏成因及分析

本文采用有限元法计算方法来进行大坝的渗流稳定计算，坝体、坝基及防渗墙的渗透系数按照地勘资料综合确定，工具采用河海大学工程力学研究所编写的水工结构有限元分析系统Autobank v7.7，计算结果如图12—13所示。

图12 稳定渗流计算结果

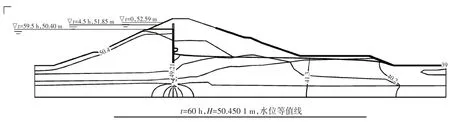
图13 非稳定渗流计算结果

根据图12—13 有限元计算结果，可以得出以下结论：坝身桩号0+300断面处的稳定渗流（正常蓄水位条件下）、非稳定渗流（校核洪水位骤降到正常蓄水位）时的渗透比降均小于土体允许比降，溢出点高程为39.20～39.70 m，位于反滤排水体顶部高程以下，最大渗流量为0.554 455 m3/d，计算上述工况的最大出逸比降为0.332，小于坝体填土允许比降0.51，即桩号0+300 断面的坝基和坝体渗透稳定性基本满足要求。

但是，渗漏各断面的具体情况不同，实际情况较难模拟。因此，根据大坝的巡检资料进行分析可得：整个坝身内遗留有建库时部队埋设的铸铁引水管，铸铁管锈蚀严重，运行中存在较大的渗流安全隐患，如图14 所示。并且，根据运行资料，溢洪道南侧坝体经过简单灌浆处理后，仍有渗漏情况发生。渗漏段坝体防渗墙为正常溢洪道南侧原浆砌石刺墙加高段，紧邻正常溢洪道，位于最大坝高段。渗漏段坝体单薄且坝体结构复杂，渗漏原因是坝内刺墙加高段存在损坏，运行中有重大安全隐患。北涵背水坡人行梯道与坝脚平台相接处有渗漏水流出逸，如图15所示。北放水涵南侧背水坡抗震平台自2010 年起高水位时有大面积潮湿、散浸，经分析判断该段坝体填筑土部分碾压效果较差、透水性强，各层填土胶结处渗透系数偏大，导致坝体浸润线偏高。同时，根据现场钻孔注水试验，岱山水库坝基基岩渗透性为弱透水，属相对不透水层；但坝体与坝基结合部位施工处理较差，存在清基不彻底问题，渗透性不满足规范要求。

图14 坝身内部铸铁引水管

图15 渗漏逸出点现场

综上所述，岱山大坝在运行中已出现严重渗流异常现象，大坝渗流性态不安全。后续结合大坝渗漏的特点及其对工程的安全影响程度，采取相应措施（布设混凝土防渗墙、土工膜、灌浆等）进行除险加固；同时，建议挖除坝身内部铸铁引水管，并加强工程管理和大坝安全监测，添加水情自动测报系统，确保大坝的安全运行。

5 结论

（1）在岱山大坝渗流预测中，BP 模型的评价指标高于RF、SVR 模型，具有高精度、鲁棒性强等特点；在考虑库水位的背景条件下，输入步长为2～3 时预测精度最高、效果最好，能较合理地预测出测压管水位的变化趋势和水位值。该模型为未来岱山大坝的安全管理及风险评估提供了一种合理方法，后续也需要多种优化算法对模型的参数进行选优，同时继续提供监测数据以便模型进行训练。

（2）有限元计算得出坝身桩号0+300 断面处的稳定渗流（正常蓄水位条件下）、非稳定渗流（校核洪水位骤降到正常蓄水位条件下）时的渗透比降均小于土体允许比降，溢出点高程均位于反滤排水体顶部高程以下，最大渗流量为0.554 455 m3/d，即坝基和坝体渗透稳定性基本满足要求。但是，结合有限元计算结果和现场调查情况分析，岱山大坝坝身内部的铸铁引水管、北涵的渗漏出逸点、溢洪道南侧的刺墙加高段渗漏等问题严重影响大坝的渗流安全。

（3）岱山大坝后续应结合大坝渗漏的特点及其对工程的安全影响程度，采取相应措施（布设混凝土防渗墙、土工膜、灌浆等）进行除险加固；同时，建议挖除坝身内部铸铁引水管，并加强工程管理和大坝安全监测，添加水情自动测报系统，确保大坝的安全运行。