楼板假定对于平面凹进框剪结构抗震计算的影响

张元琦 中石油吉林化工工程有限公司 吉林 132002

框架剪力墙作为受力状态复杂的结构形式，框架和剪力墙两类抗侧体系刚度相差较为悬殊，在水平地震作用下，楼板起到传递水平力、协调层间变形的重要作用，因而楼板的平面内变形及刚度对框剪结构抗震性能的影响不可忽略。常规结构计算分析中，一般采用楼板平面内刚度无限大的假定以简化计算，在框架剪力墙的计算中往往存在较大误差，以带有狭长楼板或楼板不连续、不规则的框剪结构尤甚，其中平面凹进的框剪结构不仅显著削弱楼板的平面内连续性，还使得位于边榀的抗侧体系不再完整，凹槽处水平地震作用没有明确传递路径，受力复杂，楼板应力集中明显，并会造成结构质量和刚度不均匀不对称，加重扭转效应。本文以平面双向均有凹进的框架剪力墙结构工程为例，研究此类结构在刚性/弹性楼板假定下地震动力响应、抗震性能的异同，为结构设计提供参考。

1 工程简介及模型建立

某工程商用公寓楼为单塔大底盘结构，地下2层车库，地上首层层高4 米，标准层层高3 米，建筑高度34 米。抗震设防烈度为8 度（0.2 g），Ⅱ类场地，抗震设防类别为丙类，建筑设计使用年限为50 年。由于首层嵌固，计算模型仅考虑地上部分，平面布置见图1。

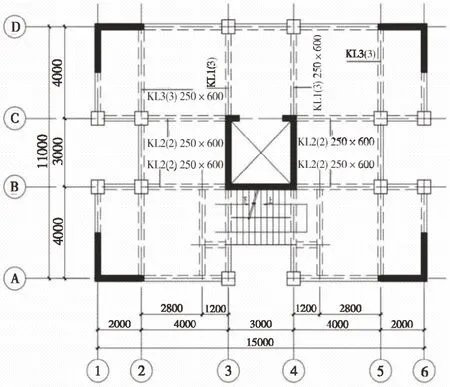
图1 标准层结构平面布置图

根据《结构设计统一技术措施》[1]，区分楼板开洞与平面凹凸的原则是：凹凸主要是建筑外立面的变化，考察结构在水平力作用下，结构抗侧体系的完整性及在平面凹凸处的传力路径；楼板开洞则是从结构内部完整性角度，考察抗侧力构件协同工作的能力。遇电梯井开洞处，宜将电梯井用剪力墙围住，可视为楼板开洞，不作平面凹进。根据上述原则及规范对建筑平面凹凸的规定，该工程Y 向凹进4 m，凹进程度4/11=0.36 ＞0.3，为一般平面不规则结构。

该建筑疏散步梯梯板采用滑动支座与梯梁连接，计算中不计楼梯刚度，仅作为静力荷载。

根据《高规》[2]7.1.4 规定，剪力墙结构底部加强部位从地下室顶板算起，高度为max{H/10，底部2 层}，一、二层剪力墙为一般剪力墙-加强位置。罕遇地震波选取Pacoima1 波，《抗规》[3]第5.1.2 条和第5.2.3 条规定，限定最大峰值加速度220 cm/s2，地面时程以X 为主向，主次向加速度比值指定为1 : 0.85，地震持续时间取15 s，加速度时程见图2。

图2 Pacoima1 波加速度时程

2 模型初始设定

建筑东西两侧凹进2 m，凹进率13.3%<30%；南侧凹进4 米，凹进率36%>30%，为平面一般不规则结构。将工程项目结构原型建入midas gen，记为MOD-0，结构模型立面见图3。

图3 MOD-0 立面示意

3 单元类型特性指定及构件材料

（1）墙单元：墙为板壳单元并考虑真实厚度。塑性铰选择钢筋混凝土纤维模型，静力及小震分析完成后更新剪力墙配筋信息，然后定义非弹性材料特性值，由程序自动生成纤维铰模型。砼本构选择《混规》[4]附录C 单轴受压本构模型（过-王准则），钢筋本构选择二折线模型，二段折线斜率取b=0.01。

（2）框架：gen 在前处理阶段不区分梁柱，均视作一般线单元；若梁柱采用纤维铰模型则迭代结果收敛性不佳，故梁柱均采用传统集中铰设定。框架柱受压弯作用，塑性铰定义为P-M-M 相关，滞回模型为修正武田三折线。修正后的三折线模型对屈服段及卸载状态予以一定校正，修正后承载能力较三折线模型略有下降，滞回曲线更为饱满，耗能能力更强（材料本构及滞回模型曲线见图4）。

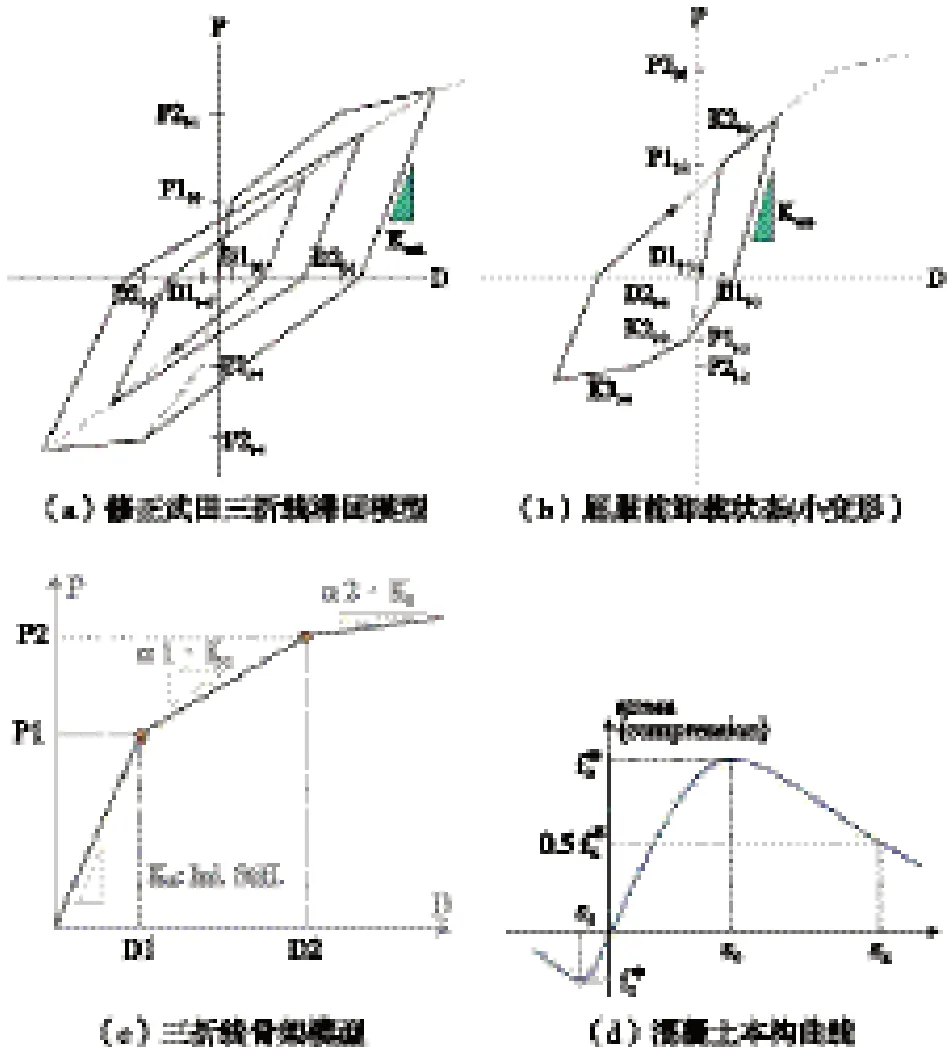
图4 材料本构及滞回模型曲线

刚度退化曲线中，第一刚度折减系数α1=0.5，第二刚度折减系数α2=0.1，P1 对应开裂阶段起点荷载，P2 对应屈服阶段起点荷载。

4 刚性假定计算偏差

根据分析结果，将初始模型MOD-0 设置为刚性楼板假定/弹性楼板假定两个子模型分别进行小震弹性分析，整理结构动力特性、凹槽处典型竖向构件内力及位移结果，见图5 及表1。内力分析结果为X 向小震单工况内力标准值，两种假定下Y向地震内力计算结果相差甚微，故未列出。

表1 弹性分析结果

结果表明，在小震弹性工况下，除电梯井的X向单片墙外，构件内力分配、结构动力特性及变形，两种假定计算差异不大；楼板假定对弹性层间位移影响甚微，可以忽略不计。由于结构平面布置中剪力墙间距、板跨较小，虽然楼板存在开洞，但仍保持较大平面内刚度，在地震作用下未产生明显的平面内变形。

整理MOD-0 在罕遇地震下，两种假定的对比结果，见表2 及图6。

图6 罕遇地震层间位移角及层间剪力对比

可见两种楼板假定在罕遇地震作用下计算结果有一定偏差，各层地震剪力存在3.3%~6.5%的偏差；弹塑性层间位移最大值出现在4、5 两层，计算偏差分别为4.6%、5.4%。采用刚性楼板假定时，结构抗侧刚度偏大，因此，尽管刚性假定下地震剪力计算结果偏大，但产生的层间位移仍小于弹性假定结果。顶层屋面板绝对水平位移见图7。

图7 顶层屋面板水平位移绝对值

位移等值线分布大体相当，但弹性模型在南侧凹槽处楼板端部产生0.6 mm 相对位移，说明楼板在罕遇地震作用下产生一定平面内变形。

剪力墙塑性铰出铰部位及屈服状态见图8~图9，取step：20s 的最终状态，铰成分指定平面内弯曲Ry。

图8 非弹性铰屈服状态

可见两组模型剪力墙出铰部位大体一致，以中部梯井根部塑性发展为最多，且各剪力墙屈服部位主要集中于底部加强2 层；两组模型墙铰屈服程度有较大区别，墙肢Q-2 在刚性模型中，底部两层延性系数为5.5/4.7，弹性模型为5.9/5.3；取4 片Q-1墙根处延性系数最大值，刚性模型为3.7/2.8，弹性模型为4.0/3.4，刚性假定下整体结构的剪力墙屈服程度小于弹性假定。故弹性假定下，剪力墙有更大塑性发展，刚度退化更多，从而进一步证明，弹性假定大震剪力较小、而位移结果反而偏大。

5 结语

对于本工程平面凹进的框剪结构，刚性楼板假定和弹性楼板假定在小震弹性计算分析中影响不大，当凹进程度不大（如算例中的Y 向地震）、剪力墙间距较小时，楼板平面内刚度较大，两种假定计算差异可忽略不计；但在罕遇地震工况下，刚性楼板假定下的分析结果无论位移指标、塑性发展程度均小于弹性假定，计算结果偏向于不安全，且该假定高估结构在弹塑性阶段的抗侧刚度，故该类型框剪结构涉及大震计算时，应慎用刚性楼板假定。

图9 非弹性铰延性系数（D/D2）