基于数值模拟的开槽法测量混凝土工作应力研究

张一，徐赵东，李今保，郭迎庆

(1. 东南大学 中国-巴基斯坦重大基础设施智慧防灾一带一路联合实验室，江苏 南京，210096；2. 江苏东南特种技术工程有限公司，江苏 南京，210008；3. 南京东瑞减震控制工程有限公司，江苏 南京，210033)

在混凝土结构的寿命期内，应力衰减、混凝土徐变、施工偏差和不均匀沉降会导致混凝土结构应力发生变化，工作应力的理论计算总是与实际应力相差很大，因此准确评估混凝土结构内的工作应力对于确保结构安全性和可靠性非常重要。测量现有混凝土结构的工作应力一直是一个难题，混凝土材料的不均匀性和随机性、应变测量技术等因素导致应力测量结果存在较大的离散性和误差。

局部破损检测技术即应力释放法，最初由MATHAR[1]提出，用来对钢结构构件中的残余应力进行测量。对金属构件所测区域进行切割或钻孔，使所测区域的应力得到释放，测量应力释放前后测点处的应变变化量，经计算得到残余应力[2-3]。

近几十年来，科研人员对应力释放法进行了大量的研究，并逐渐将其应用于混凝土材料的应力检测中。为了克服解析方法仅适用于应力沿厚度方向均匀分布的薄板的局限性，SCHAJER[4-6]提出了以标定系数为核心的积分法与幂级数法来识别沿深度方向的非均匀分布应力场，其适用性、稳定性和精度都得到了显著增强。

TRAUTNER等[7-8]将应力释放法应用于混凝土结构，使用基于表面位移的影响函数，结果具有了良好的理论精度，但由于释放位移量级极小，实际应用难度较大。影响函数是标定系数的连续形式，目前已发展为广泛使用的方法[9-12]。国内外学者逐步将影响函数应用到混凝土工作应力的检测之中，对影响函数不断进行优化以提高识别精度[13-14]。

混凝土应力释放法按钻孔或切割形式的不同，可分为盲孔法、圆孔法和开槽法[15-19]。开槽法是在圆孔法的基础上进行改进和创新得来的，按开槽形状可以分为直线形开槽法(横槽)和方形开槽法(方槽)。开槽法在实际工程中易于施工，尤其是在只关注单向应力问题时，对混凝土结构产生的损伤较小。因此，近年来部分学者对开槽法进行了深入研究，并将其应用到混凝土的应力检测中[20-25]。但是实际混凝土结构大多处于复杂受力状态，开槽法的测量结果必定与混凝土结构真实受力状态存在一定的差别，这一缺点限制了开槽法在实际工程中的应用。

本文作者对应力释放法中的开槽法进行研究，针对单向应力状态下的混凝土受压构件，采用数值模拟的分析方法研究开槽形状、开槽间距、开槽长度等因素在不同开槽深度下对应力释放程度的影响，并提出了一种新的分步测量方法。

1 基本原理

开槽法是一种局部损伤检测方法，用于评估混凝土结构内的工作应力。开槽过程中，开槽区域内外应力逐渐释放，开槽区域周围的混凝土发生弹性变形。应变传感器根据工作应力方向固定在测点上，随着开槽深度增加，应变传感器开始测量混凝土释放的弹性应变。开槽达到一定深度后，测点处混凝土的工作应力完全释放。根据应变传感器测得的应变变化值，通过混凝土弹性模量计算构件的工作应力。

式中：σ为混凝土的工作应力；E为混凝土的弹性模量；ε为释放的弹性应变。

2 数值模拟与分析

2.1 计算模型与参数

本文以单向应力状态下的受压构件为研究对象进行数值模拟，使用有限元软件建模分析，选用的模型长×宽×高为3 000 mm×400 mm×400 mm，软件内模型示意图如图1所示。模型中的混凝土强度等级为C30，钢筋的强度等级为HRB400。为方便后续对计算结果进行分析，对开槽间距H、开槽长度L、中心测点以及应力释放区域长宽比λ等因素进行规定，如图2所示。其中应力释放区域长宽比λ的计算公式为

图1 模型示意图Fig. 1 Schematic diagram of model

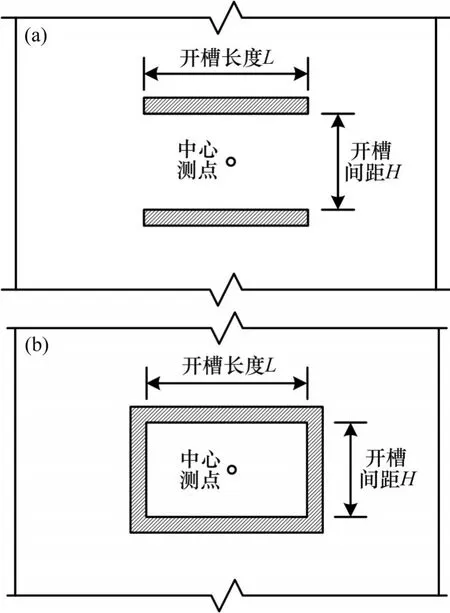
图2 开槽间距和开槽长度示意图Fig. 2 Schematic diagram of slotting spacing and slotting length

式中：λ为应力释放区域长宽比；L为开槽长度即应力释放区域长度；H为开槽间距即应力释放区域宽度。

测点应力释放率α的计算公式为

式中：σy为不同开槽深度下的测点处的Y向应力；σ0为测点处的初始Y向应力。

2.2 压应力对应力释放程度的影响

针对压应力(即构件工作应力)对应力释放的影响程度进行分析，采用轴压比u进行控制，选取轴压比u为0.1、0.3、0.5 和0.7 的4 种工况。开槽形状选取方槽H=100 mm、L=100 mm、λ=1，开槽深度取10 mm 为一步，从0 mm 分步计算至150 mm得到不同开槽深度下开槽区域中心测点处Y向应力并计算得到每一步开槽深度下的应力释放率。Y向应力的分析结果如图3所示，应力释放率的分析结果如图4所示。

图3 不同压应力下Y向应力随开槽深度的变化Fig. 3 Variation of Y-directional stress with slotting depth at different pressure stresses

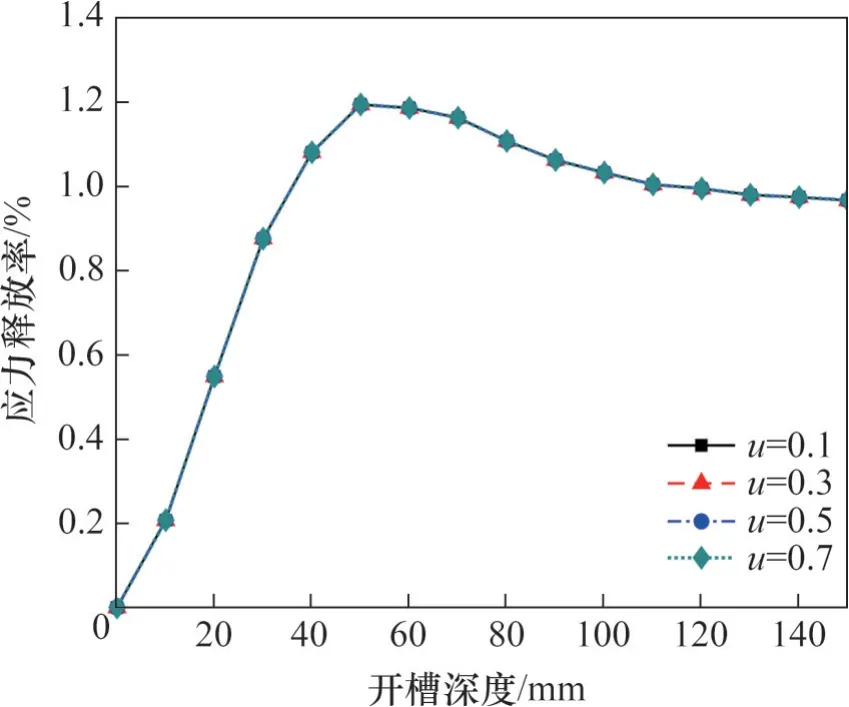
图4 不同压应力下应力释放率随开槽深度的变化Fig. 4 Variation of stress release rate with slotting depth at different pressure stresses

由图3可以看出：压应力只对构件测点处初始Y向应力和每一步应力释放值有影响，对应力完全释放即应力释放率为0时的开槽深度没有影响。随着开槽深度增加，Y向应力从初值逐渐减小，4 种工况的Y向应力均在开槽深度为36 mm 时完全释放。应力释放率到达0 时，开槽深度继续增加，Y向应力随之反向增大，在开槽深度为50 mm 时达到反向最大值，其中初始Y向应力越大的工况反向应力最大值越大。当开槽深度为50～150 mm时，Y向应力逐渐减小至0 MPa附近。

由图4 可以看出：在开槽深度相同时，4 种轴压比下测点的应力释放率基本相同。由此可见，压应力对每一步的应力释放率没有影响，即不同开槽深度下的应力释放程度与构件当前的工作应力无关。因此，开槽法可以广泛用于检测混凝土构件的工作应力，不同开槽深度下的应力释放值不受构件工作应力的影响。

2.3 开槽长度对应力释放程度的影响

2.3.1 横槽的开槽长度对应力释放程度的影响

针对横槽的开槽长度L对应力释放程度的影响进行分析，开槽间距H选取50 mm，开槽长度L选取30、35、40、45、50、60、70、80、90和100 mm这10 种工况进行分析，即长宽比λ分别为0.6、0.7、0.8、0.9、1.0、1.2、1.4、1.6、1.8和2.0。从0 mm分步计算至100 mm得到不同开槽深度下开槽区域中心测点处Y向应力，结果如图5所示。

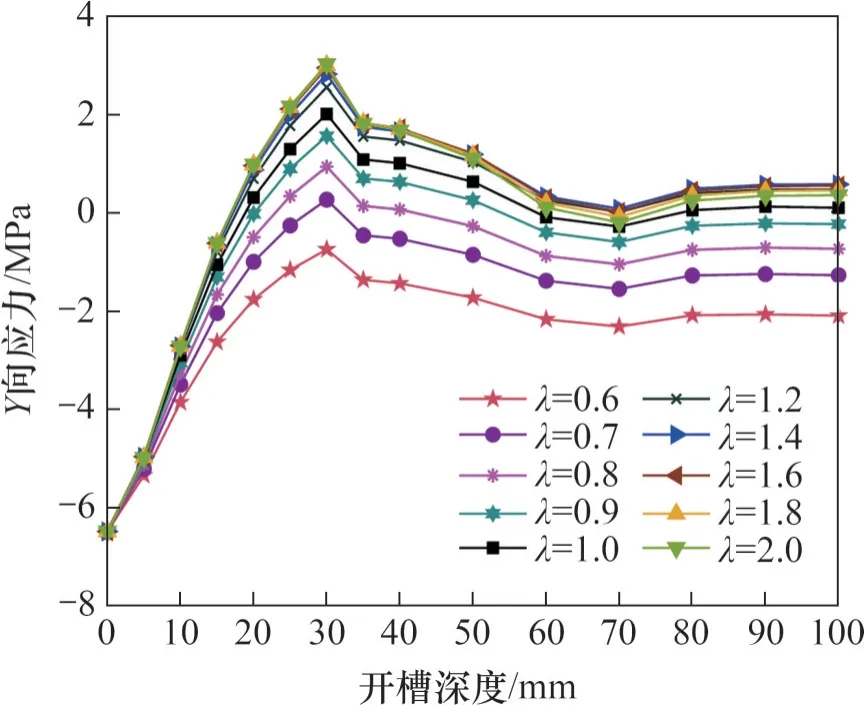
图5 横槽不同开槽长度下Y向应力随开槽深度的变化Fig. 5 Variation of Y-directional stress with slotting depth at different slotting lengths of horizontal slot

由图5可以看出：开槽长度对横槽应力释放程度的影响可以根据长宽比λ分为两种情况进行分析，即长宽比λ≤1与λ＞1。

当长宽比λ≤1时，即开槽长度L小于等于开槽间距H时，Y向应力随开槽深度的变化趋势一致，但每种工况之间差值较大。随着开槽深度增加，Y向应力从初值开始减小，在开槽深度为30 mm 时应力释放率达到最大值，随后Y向应力逐渐稳定到某一负值附近。开槽长度L越长，应力释放越快，应力完全释放时的开槽深度也较小。但当λ=0.6时，不管开槽深度为多大，中心测点的Y向应力均未达到完全释放的程度。

当长宽比λ＞1时，即开槽长度L大于开槽间距H时，Y向应力随开槽深度的变化趋势一致，但每种工况之间差值较小。λ＞1 的5 种工况中Y向应力最大差值出现在开槽深度为30 mm时，Y向应力最大差值与初始Y向应力的比值为7.24%；每步开槽深度下Y向应力最大差值与初始Y向应力的平均比值为2.74%。由此可见，长宽比λ＞1 的情况下，不同开槽长度之间的Y向应力差值较小。因此，在检测切割时只要保证长宽比λ＞1，检测结果较为精准。

2.3.2 方槽的开槽长度对应力释放程度的影响

针对方槽的开槽长度L进行分析，与2.3.1 中研究横槽开槽长度的工况相同，开槽间距H选取50 mm，开槽长度L选取30、35、40、45、50、60、70、80、90 和100 mm 这10 种工况进行分析，即长宽比λ分别为0.6、0.7、0.8、0.9、1.0、1.2、1.4、1.6、1.8 和2.0。从0 mm 分步计算至100 mm得到不同开槽深度下开槽区域中心测点处Y向应力，结果如图6所示。

图6 方槽不同开槽长度下Y向应力随开槽深度的变化Fig. 6 Variation of Y-directional stress with slotting depth at different slotting lengths of square slot

由图6 可以看出：Y向应力随开槽深度的变化趋势一致，Y向应力从初值开始减小，在开槽深度为30 mm时应力释放率达到最大值，随后Y向应力逐渐稳定到0 MPa附近。Y向应力最大差值出现在开槽深度为30 mm时，Y向应力最大差值与Y向应力初值的比值为7.26%；每步开槽深度下Y向应力最大差值与Y向应力初值的平均比值为2.81%。由此可见，当开槽形状为方槽时，开槽长度对不同开槽深度下中心测点的Y向应力影响较小。因此，在检测切割时，方槽可以用于结构狭小区域，开槽间距一定时，开槽长度变化所导致的应力释放值差值较小，检测结果较为精准。

2.3.3 横槽与方槽的对比

由2.3.2 可知，在开槽形状为方槽时，开槽长度L对不同开槽深度下中心测点的Y向应力影响较小，因此选取方槽长宽比λ=1的工况为代表值，代入到2.3.1 节中横槽不同开槽长度下Y向应力随开槽深度H的变化中。为便于区分，方槽长宽比用λ0表示，结果如图7所示。

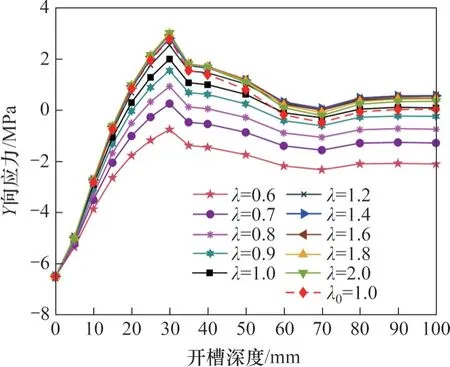
图7 横槽与方槽的Y向应力对比Fig. 7 Comparison of Y-directional stress between horizontal slot and square slot

由图7 可见：当0≤H≤40 mm 时，长宽比λ0=1的方槽Y向应力与长宽比λ＞1 的横槽Y向应力之间变化趋势一致，差值较小。当开槽深度为30 mm时，λ0=1 的方槽Y向应力与λ=1.2 的横槽Y向应力之间的差值与初始Y向应力的比值为3.57%；与λ=2.0 的横槽Y向应力之间的差值与初始Y向应力的比值为3.67%。当40＜H≤80 mm时，长宽比λ0=1的方槽Y向应力逐渐减小至0 附近，与长宽比λ＞1 的横槽Y向应力之间的差值逐渐变大。当80＜H≤100 mm 时，长宽比λ0=1 的方槽Y向应力逐渐稳定在0 附近，与长宽比λ=1 的横槽Y向应力之间差值较小。因此，在开槽深度较小时，方槽与相同开槽间距、长宽比λ＞1的横槽之间可以相互替代，两种开槽形状的中心测点的Y向应力之间差值较小，趋势一致。

2.4 开槽间距对应力释放程度的影响

针对开槽间距H进行分析，开槽长度L选取50、60、70、80、90 和100 mm 这6 种工况进行分析。为了避免开槽长度L不同对结果造成影响，控制6 种工况的长宽比λ=1 即开槽长度L均等于开槽间距H。从0 mm 分步计算至100 mm 得到不同开槽深度下开槽区域中心测点处Y向应力，结果如图8和图9所示。

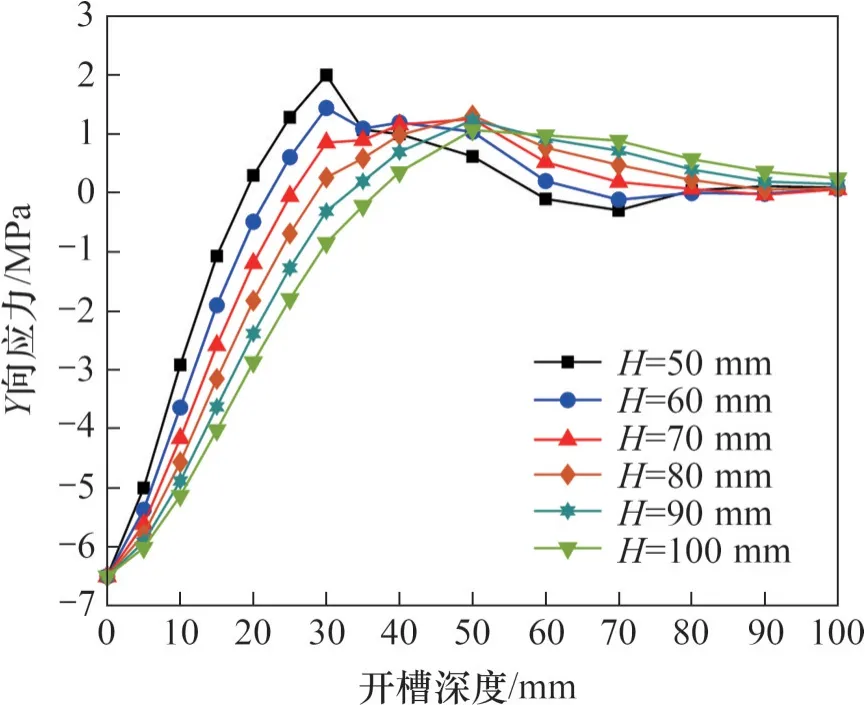
图8 横槽不同开槽间距下Y向应力随开槽深度的变化Fig. 8 Variation of Y-directional stress with slotting depth at different slotting spacings of horizontal slot

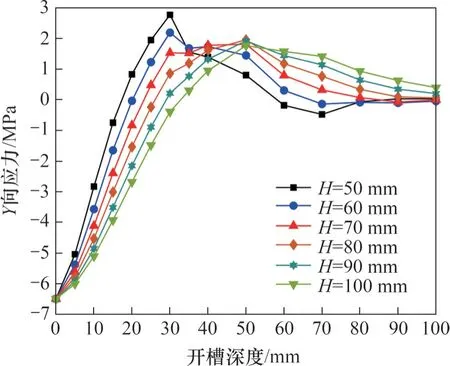
图9 方槽不同开槽间距下Y向应力随开槽深度的变化Fig. 9 Variation of Y-directional stress with slotting depth at different slotting spacings of square slot

由图8和图9可见：横槽与方槽不同开槽间距下的应力释放趋势相同。在开槽过程中，中心测点的Y向应力将经历三个阶段。在第一阶段，随着开槽深度增加，Y向应力逐渐减小，直到应力完全释放。对于应力完全释放的开槽深度称为零应力深度或应力完全释放深度，该深度在第一阶段结束后首次达到。开槽深度继续增加，应力释放进入第二阶段。此时，应力沿相反方向增加，直到达到最大值(远小于初始Y向应力)。最后进入第三阶段，Y向应力从反向最大值再次逐渐接近于0 MPa。在实际应力测量中，第一阶段的应力释放程度的变化应该是关注的焦点。因此，开槽间距越小，中心测点处的应力释放速率越大，应力完全释放深度越小。

2.5 数值模拟与试验结果对比分析

为验证数值模拟结果的准确性和适用性，选取文献[22]中6 个测点的试验结果进行对比分析，如表1所示。由表1可以看出：在相同的开槽深度下，横槽与方槽之间的应力释放率差值较小，这也验证了前文得到的结论：长宽比λ=1的方槽与相同开槽间距H、长宽比λ＞1的横槽之间可以相互替代，两种情况中心测点的应力差值较小。试验应力释放率与数值模拟结果之间的差值均较小，验证了数值模拟方法的准确性和开槽法的适用性。值得注意的是，文献[22]中扣除了水、温度和切割扰动影响后的试验结果具有较高的精度，但实测过程中对测点应变的影响与许多因素有关：包括混凝土含水量、骨料质量、钢筋位置和应变片尺寸等，由此产生扰动对测点应变的影响也会有所不同，这些因素的影响也将是未来研究的重点。

表1 应力释放率的数值模拟与试验结果对比Table 1 Comparison of numerical simulation and experimental results of stress release rate

3 开槽区域的应力分布规律分析

根据应力释放的原理对混凝土进行开槽处理后，开槽区域周围的混凝土将发生应力释放，导致局部应力重新分布。对于测量混凝土工作应力的槽孔，相邻开槽的位置应不受其他开槽区域的局部影响。在实际测量中，应在开槽区域周围合理选取测点，保证能够灵敏、准确地测量开槽引起的应变变化。测点选取不合理、测点处应力释放率小以及应变传感器的灵敏度弱等因素，都可能导致应变测量失败。

提取槽内区域和槽外区域的各测点不同开槽深度时的Y向应力，分析开槽区域的应力释放范围。选取H=50 mm、L=50 mm、λ=1的横槽与方槽进行分析，由于横槽与方槽均为对称开槽，因此测点从中心测点开始向一侧选取，测点位置如图10 所示。开槽深度从0 mm 分步计算至100 mm 得到不同开槽深度下各测点处Y向应力，结果如图11和图12所示。

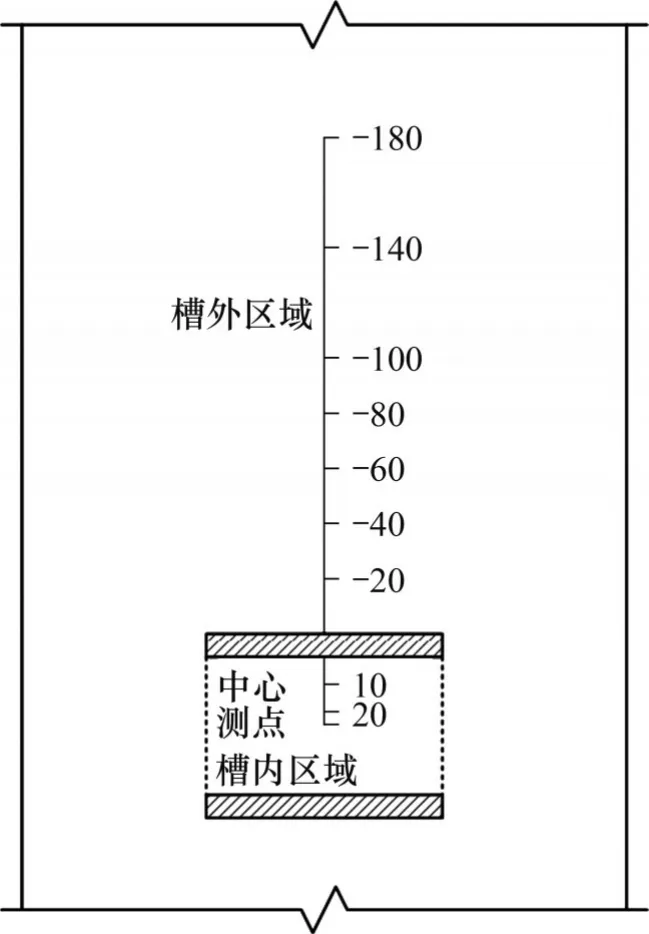
图10 应力释放范围分析测点示意图Fig. 10 Schematic diagram of measurement points for stress release range analysis

图11 横槽各测点Y向应力随开槽深度的变化Fig. 11 Variation of Y-directional stress with slotting depth at different measurement points of horizontal slot

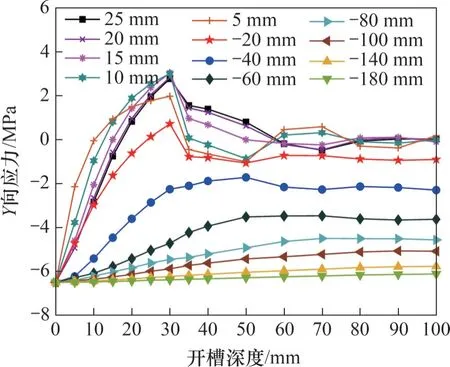
图12 方槽各测点Y向应力随开槽深度的变化Fig. 12 Variation of Y-directional stress with slotting depth at different measurement points of square slot

横槽与方槽的槽内区域内选取5 个测点，5 个测点与槽内边缘的距离分别为5、10、15、20 和25 mm(中心测点)。由图11 和图12 可见：25 mm(中心测点)与20 mm两个测点之间Y向应力差值较小，横槽每步开槽深度下的平均差值与初始Y向应力的比值为1.43%；方槽的比值为1.45%。开槽深度为0～30 mm 时，10、15、20 和25 mm 四条应力释放曲线变化趋势一致，越靠近凹槽，应力释放速度越快；5 mm工况下的应力释放曲线与中心测点的差值较大，这是由于距离凹槽过近，受到应力集中等因素的影响。考虑到凹槽切割扰动、测量差值较大等因素的影响，离凹槽过近的位置不适合进行应变测量，因此建议选取中心测点以及上下10 mm 范围内作为外贴应变片的位置，测量结果稳定，误差在可接受的范围内。

横槽与方槽的槽外区域选取7 个测点，7 个测点与槽外边缘的距离分别为20、40、60、80、100、140和180 mm。测点越靠近凹槽，应力变化越大，应力释放曲线变化趋势越接近于槽内区域测点的应力释放曲线变化趋势。因此，圆孔法测点通常选取距离切割圆孔外0～15 mm 的位置。测点距离凹槽180 mm 时，应力释放曲线接近为直线，开槽深度为100 mm时，横槽的应力释放率为3.22%；方槽的应力释放率为5.89%。因此，相邻凹槽至少应保持在200 mm之外，可认为不受相邻凹槽的影响。

对于横槽开槽法和方槽开槽法，与圆孔法相比，其优点在于可以将测点选取在槽内区域，解决了圆孔法孔内应变信息不能连续输出的问题。圆孔法由于钻孔机器的影响，测点只能选取在圆孔外部区域，因此测量结果受测点与圆孔之间的距离影响较大，越靠近圆孔测量结果越精准，但同时会受切割扰动影响。而开槽法的测点可以选取在测量区域中心位置，测量结果精准，受切割扰动等因素影响小。

4 分步测量方法

在使用圆孔法或开槽法进行实际测量时，通常的做法是钻孔或开槽至零应力深度或应力完全释放深度，得到测点处的释放应变，从而反推测点处的工作应力。但是这种方法测量得到的工作应力误差较大，分析其原因：第一，零应力深度与开槽形状、开槽间距、开槽长度等因素关系密切，在切割过程中开槽长度等因素容易发生变化，因此，零应力深度也会随之变化，导致误差变大；第二，在通常情况下，由于切割扰动等因素的影响，难以精确控制混凝土切割机器切割深度恰好达到零应力深度，导致误差存在。

为了减小测量误差，提出了一种新的分步测量方法。设置合理的开槽分步距离，通过测量每一步开槽深度下的应力释放值，与数值模拟的结果相结合，利用多步优化结果反推测点处工作应力。分步测量方法与常规测量方法最大的区别在于不需要时刻关注零应力深度的变化，而是可以采用合理的分析步距和分析步数，最大程度地减小误差。

由2.2分析结果可知，测点处现存工作应力对每一步的应力释放率没有影响。设置每一步开槽深度为5 mm，由数值模拟可以得到开槽深度从0 mm开始每步深度(5 mm)下的应力释放率α0，α1，α2，α3，…，αn(α0=0)。同时，在构件上采用相同开槽形状从0 mm开始切割，得到每步深度(5 mm)下中心测点处的应变测量值ε0，ε1，ε2，ε3，…，εn(ε0=0)。因此，工作应力σ可以通过以下公式进行计算：

式中：n为测量步数；αi为数值模拟中第i步的应力释放率；εi为实际测量中第i步的应变测量值。

5 结论

1) 提出了一种分步方法测量混凝土的工作应力，无需关注开槽过程中的零应力深度变化，通过测量多步开槽深度下的应力释放值，与数值模拟的结果相结合，减小测量误差。

2) 压应力(工作应力)只对初始应力和每一步应力释放值有影响，对不同开槽深度下的应力释放率没有影响。

3) 开槽长度对长宽比λ≤1的横槽影响较大，开槽长度L越大，应力释放速率越大，应力完全释放深度越小；对长宽比λ＞1的横槽影响较小。开槽长度对方槽的影响较小，在开槽深度较小时，方槽与相同开槽间距、长宽比λ＞1的横槽之间可以相互替代，两种情况中心测点的Y向应力之间差值较小。

4) 横槽与方槽在不同开槽间距下的应力释放趋势相同，开槽间距越小，应力释放速率越大，应力完全释放深度越小。

5) 开槽法解决了圆孔法孔内应变信息不能连续输出的问题。应力释放时，槽内区域比槽外区域的应力变化更敏感和准确，选取中心测点以及上下10 mm范围内粘贴应变片，测量结果稳定。