考虑开挖全过程的基坑坑外任意地表沉降实用计算方法

程康，徐日庆，应宏伟，李冰河，张金红

(1. 中铁十一局集团有限公司，湖北 武汉，430061；2. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058；3. 浙江省城市地下空间开发工程技术研究中心，浙江 杭州，310058；4. 河海大学 岩土工程科学研究所，江苏 南京，210098；5. 浙江省建筑设计研究院，浙江 杭州，310058)

以杭州为例，“十三五”期间城市地铁新开通里程近200 km，在地铁隧道沿线进行基坑开挖难以避免。而在建筑物、管线密集的软土地区进行基坑开挖将不可避免地对邻近既有构筑物带来扰动，如引起路面不均匀沉降、地下管线变形，甚至会引起结构的开裂和破坏[1-4]。由此可见，对基坑开挖诱发的坑外地表沉降进行预测具有较重要的现实意义。当前，针对基坑开挖诱发坑外地表沉降问题，钱建固等[5]将基坑开挖诱发的地表沉降问题简化为平面应变条件下的位移-位移弹性边值问题，结合镜像法推导了基坑刚性挡墙在平移、绕墙趾转动、绕墙顶转动下的地表沉降理论解，张戎泽等[6]通过室内模型试验，验证了该理论解的正确性；为进一步考虑挡墙变位模式，顾剑波等[7]将挡墙任意变位模式分解为梯形刚性模式和抛物线柔性模式，然后求解平面应变方程，从而推导了柔性挡墙在任意变位模式下的地表沉降公式。上述理论方法推导严谨，为类似工程问题的求解提供了很好的途径。但采用上述方法时，只有已知围护挡墙的变形分布才能进一步给出坑外地表沉降的预测值。

相较于理论分析法，数值方法则能够考虑基坑开挖过程中土体变形特性及深基坑工程的复杂性，并且可以结合基坑开挖及支护结构施工顺序进行模拟，因此被广泛应用与基坑工程中。基于工程实测和数值模拟，郑刚等[8]探究了基坑围护挡墙最大侧移所在位置对开挖性状的影响，发现可适当调整围护结构最大侧移发生位置以减小开挖对环境产生的不利影响。CHEN等[9]以某紧邻宁波地铁1号线的深基坑为研究对象，结合室内试验和现场实测资料，建立基坑-隧道共同作用的三维有限元模型。结果表明：基坑的分区开挖对邻近既有隧道的保护作用效果明显，而隔断墙及被动区土体加固效果较差。ZHANG等[10]采用硬化土(HS)模型进行了一系列三维有限元分析，给出了黏土强度、墙体刚度、开挖长度、开挖深度和宽度与墙体最大挠度包络线间的关系式。但数值法计算相对复杂，耗时较长，且结果的准确性依赖于土层参数及本构关系的合理选取。

此外，被从业人员广泛使用的还有实测分析法。应宏伟等[11]研究了杭州深厚软黏土中某深大基坑开挖的变形性状，发现时空效应是影响软黏土中大型基坑坑外水平位移的重要因素。YING等[12]对杭州地区10 个采用排桩墙为支撑的深基坑变形特点进行分析时发现，基坑开挖宽度对挡墙最大挠度的影响不可忽略。程康等[13]以杭州某30.2 m 深大基坑工程以及16 个杭州基坑案为研究对象，提出了基于基坑开挖面积与地连墙最大侧移之间的经验关系式。实测分析法简便实用，所获结果及结论对于预测墙后地表沉降及用于数值结果的校验具有较好的指导作用。

因此，在上述研究的基础上，本文作者以收集到的16 个杭州地铁基坑为研究对象，首先，建立起杭州地铁基坑施工的标准模型及土层模型，并以此为基础进行数值建模；接着，将上述数值与已有工程案例的实测值、既有文献值进行对比，验证数值模型的准确性，在此模型的基础上进一步分析其各开挖阶段变形性状。最后，结合实测统计、数值模拟以及理论分析，提出可考虑基坑开挖过程的坑外地表沉降分布的新预测方法。其优势在于：无需获知基坑围护挡墙的变形分布，即可给出坑外任意地表的沉降预测值；较之于既有研究大都只考虑基坑开挖至坑底时的坑外沉降，所提方法可动态考虑基坑开挖全过程中的地表沉降。研究成果可为合理预测基坑开挖对坑外地表影响提供一定理论支持。

1 地铁车站基坑标准化

有关杭州地区深基坑变形分析大多以单一基坑为对象进行研究，然而，研究所获规律往往对其他不同类型、不同规模、不同施工方法的基坑并不适用。地铁基坑是城市建设中常常遇到的类型，通常一个城市地铁基坑的各类参数(如基坑的长、宽、深)、围护结构以及施工方法等都比较接近。因此，有必要以这类基坑为研究对象，分析其变形特点，总结共性规律，以期获得适用范围更广、普适性更好的结论。研究成果亦可为类似地区同类工程的开展提供一定指导。

16 个杭州地区支护形式为“内支撑+地连墙”的地铁车站深基坑工程参数如表1所示。通过对16个深基坑工程围护结构的参数、土层基本参数、深基坑开挖过程及每层开挖深度等进行统计分析，得到杭州地区地铁基坑各项基本参数的标准化模型。

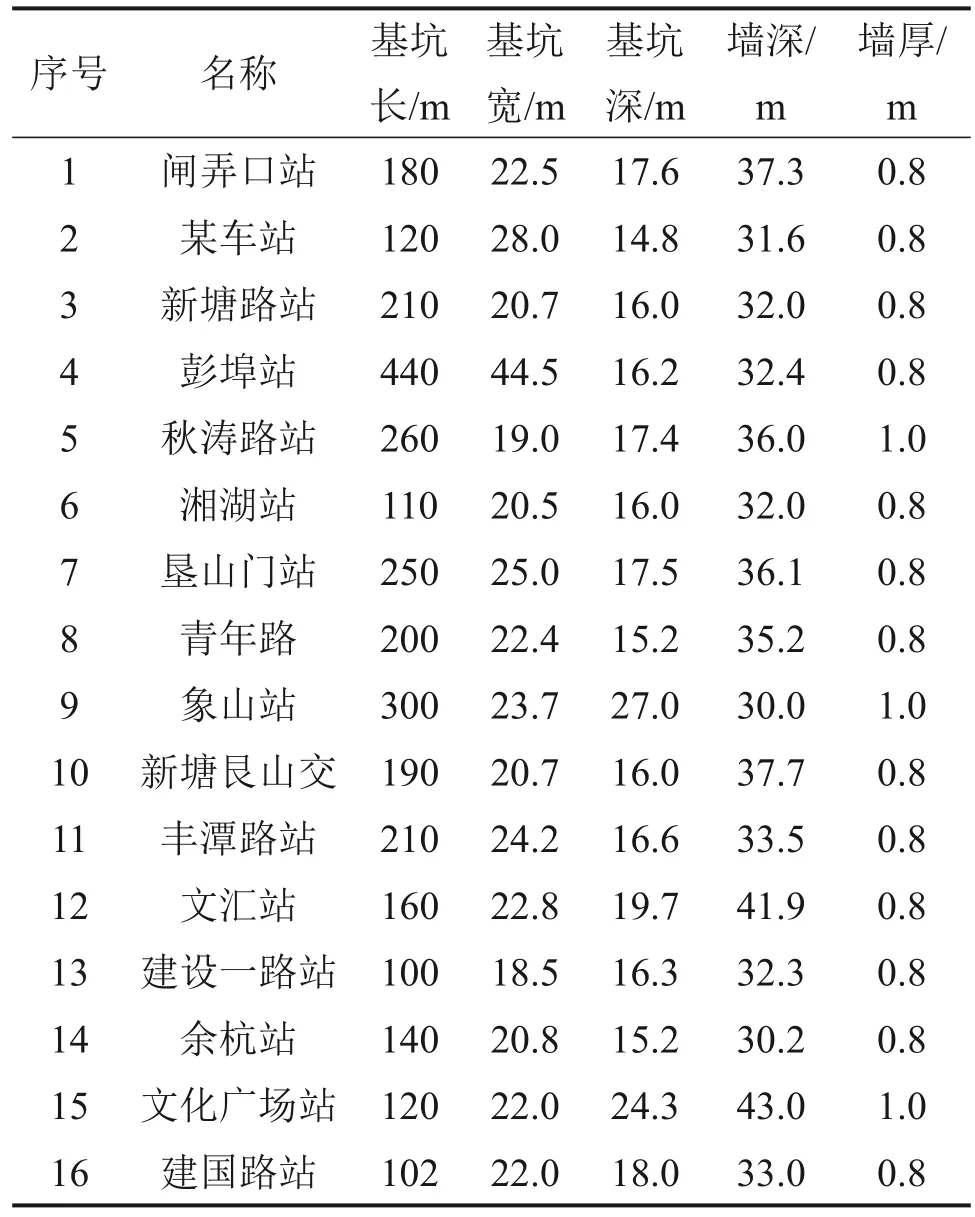
表1 地铁车站基坑参数统计Table 1 Parameter statistics of subway station basement

杭州地区地铁基坑的标准化长L、宽B、最终挖深He分别为190 m、20 m、17.5 m。采用厚为800 mm、长为37 m 的地下连续墙以及5 道支撑作为支撑围护系统，其中，地下连续墙刚度为18 GPa，首道由截面长×宽为800 mm×800 mm 的混凝土支撑，在水平方向布置间距为6 m；第二、三道由截面长×宽为609 mm×16 mm 的Q235 钢支撑；第四、五道为截面长×宽为800 mm×16 mm 的Q235 钢支撑，第二、三道和第四、五道钢支撑在水平方向上的布置间距分别为2 m 和4 m。表2 所示为标准化地铁基坑的施工开挖过程及相应标高。

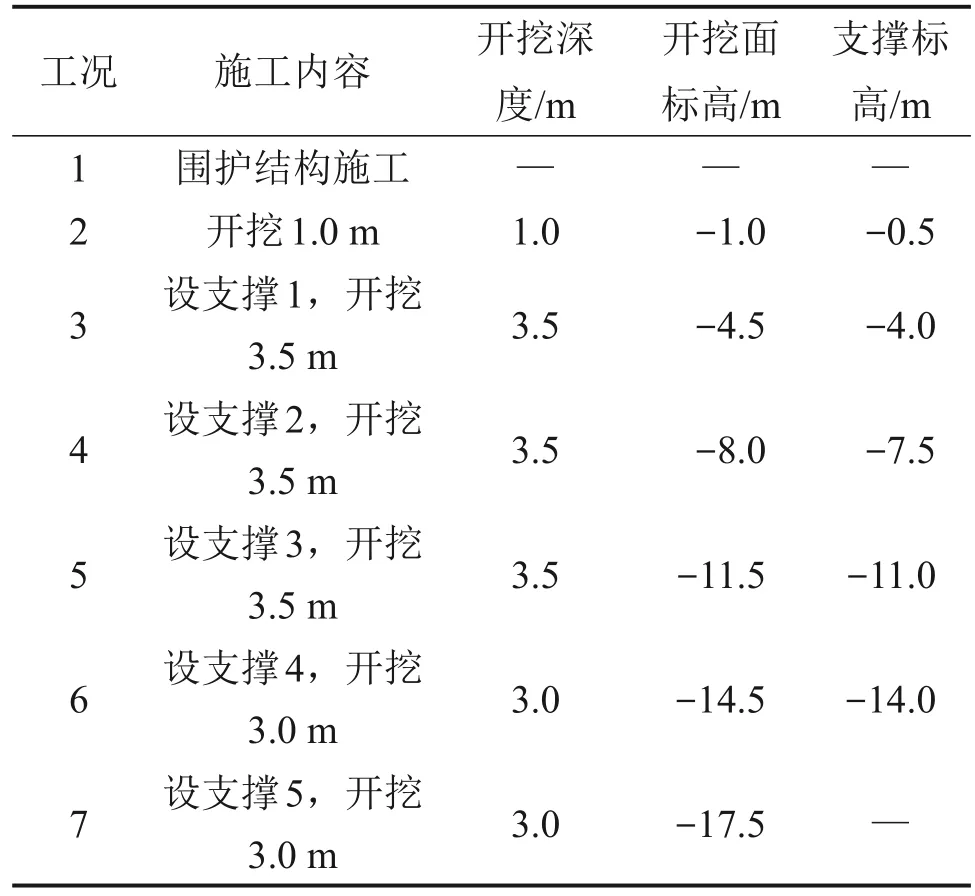
表2 基坑开挖工况Table 2 Excavation conditions of basement

2 标准化模型合理性验证

采用通用三维有限元软件PLAXIS3D 进行数值计算，沿上述标准化基坑长边的中轴线取其1/2进行有限元分析，基坑分为标准段和端头井2 部分，其中，标准段长×宽为80 m×20 m，端头井长×宽为15 m×24 m。为消除模型范围对计算结果的影响，计算边界取基坑3.5倍开挖深度以外[14]，即模型范围(长×宽×高)取155 m×140 m×60 m。模型顶面自由，侧面设置水平约束，底面设置固定约束。在计算过程中，初始应力生成后和基坑开挖前位移均重置为零。大量工程实测和研究表明，基坑周围除少数区域发生明显的塑性变形外，其余大部分区域土体处于小应变状态，且整个开挖以卸载为主。因此，考虑土体小应变特征与卸载特征的土体模型理论上更适合于基坑开挖数值分析[15]。本文采用HSS 本构模型，杭州城东地区土层的小应变参数见表3[16-18]。图1 所示为三维有限元模型的网格图，包含41 331个单元，79 865个节点。表3 所示为数值模型中地连墙以及隔离墙的相关参数。本文所建立的杭州地铁深基坑标准模型与闸弄口站基坑的几何参数类似，且闸弄口站亦位于杭州城东区，其相关参数与本数值模型所采用的参数有较好的一致性，因此，可将本数值模型的计算结果与文献[19]的相关监测结果进行对比，从而验证有限元分析结果的可靠性。

表3 杭州城东地区典型土层参数Table 3 Parameters of typical soil layers in east area of Hangzhou

图1 三维有限元网格图Fig. 1 3D finite element mesh

图2 所示为在基坑开挖完成(即工况7)时地表沉降及地连墙侧移的三维数值模拟结果与实测值对比曲线。由图2可见，由本文数值解得到的坑外地表最大沉降出现在距挡墙0.45He处，最大沉降为0.12%He；挡墙最大侧移则发生在0.5He深度处，最大侧移为0.24%He，达到了地表最大沉降的2倍。与实测值相比，不论是坑外地表沉降还是基坑挡墙水平挠曲变形，实测值和数值解均较吻合。这初步验证了本三维模型的准确性。此外，图2还给出了由王卫东等[20]提出的软土地区板式支护基坑最大变形预测公式计算得到的简化解。王卫东等[20]认为当挖深He大于7 m 时，挡墙最大侧移δhm发生在距地表0.5He处，且墙顶、底的侧移分别为0.05δhm和0.1δhm，而开挖对坑外地表的主影响区为距挡墙0～2He范围内，次影响区在2He～5He范围内，最大沉降发生在距离墙后0.5He处，紧靠墙体处的沉降为最大沉降0.5倍。经对比发现，在坑外地表沉降上，简化解略小于数值解，在挡墙变形上，简化解则是略大于数值解，综合变形趋势以及变形大小，简化解与数值解较吻合。因此，可在本数值模型的基础上进一步分析各开挖阶段性状。

图2 工况7地表沉降及地连墙侧移数值解与实测值对比Fig. 2 Comparison of numerical solution and test values of ground surface settlement and lateral wall displacement of excavation 7

在基坑各开挖阶段下，挡墙侧移和坑外地表沉降随开挖的发展情况如图3 所示。由图3 可见，各开挖阶段坑外地表沉降数值解均在TAN 等[21-22]提出的软土地区基坑的地表沉降包络线内，而且在形态上也基本一致，这间接证明了本数值模型解的有效性。此外，在坑外地表的沉降分布上，杭州地区地铁车站基坑开挖后的沉降分布与欧章煜[23]修正后的沉降分布一致性良好，即地表沉降主影响区为距挡墙0～He，次影响区为墙后1He～2He处，最大地表沉降出现在距挡墙1/3He处，由此进一步证明数值模型和材料参数的可靠性。

图3 基坑标准化模型分步开挖的地表沉降及地连墙侧移Fig. 3 Surface settlement and lateral wall displacement of each excavation condition of subway station foundation pit

3 考虑基坑开挖过程的坑外地表沉降分布预测

3.1 横向变形（垂直基坑长边）分布规律

在基坑不同开挖阶段下，x=0断面处(对应图2)的坑外地表横向沉降分布曲线如图4 所示，其中，s为距基坑外边缘的垂直距离，δv为地表沉降，H为基坑各开挖阶段的挖深，svmax为地表最大沉降。由图4可见：地表沉降曲线近似呈“勺”状分布或“三段式”折线分布。地表沉降受开挖深度影响十分明显，随着挖深增加，地表沉降显著增大，显然，与基坑浅部土体的开挖相比，深部土体的开挖可使更多的应力释放，进而产生更大的地表沉降，这进一步验证了杭州软土地区基坑开挖的深度效应[13]。此外，随开挖深度H的增大，地表最大沉降δvmax的发生位置smax也逐渐增大，地表沉降δv=0 出现的位置基本保持在s=50 m 附近，近似为基坑挖深的3倍。

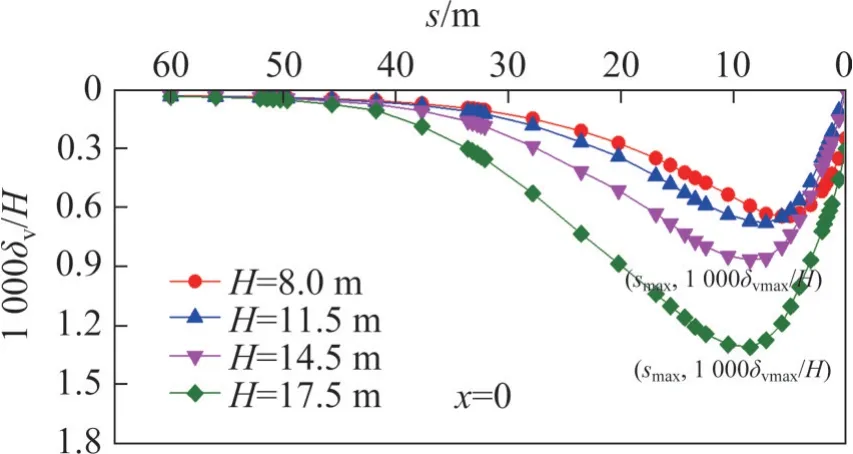
图4 不同开挖深度下地表横向沉降Fig. 4 Surface transverse settlement for different excavation depths

3.2 横向变形(垂直基坑长边)分布预测及验证

由图4可知：δvmax/H以及地表最大沉降所在位置smax受基坑挖深影响明显。若能准确地预测各开挖阶段下的δvmax/H及smax，则可较准确地得出各开挖阶段的地表沉降曲线分布。图5和图6所示分别为δvmax/H、smax与H的关系曲线。当H≥7 m 时，相应的拟合式如式(1)和式(2)所示。

图5 基坑挖深H与1 000δvmax/H的关系Fig. 5 Relationship between excavation depth H and 1 000δvmax/H

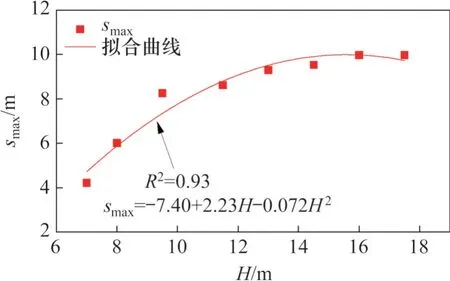
图6 基坑挖深H与地表最大横向沉降位置smax的关系Fig. 6 Relationship between excavation depth H and location smax of the maximum surface transverse settlement

由此可知：若已知基坑任意阶段的开挖深度，则可得出对应的δvmax/H及其所在位置smax。基于上述分析并结合式(1)和式(2)，考虑基坑开挖过程的地表横向沉降“三折线”分布的简化计算式如下：

由式(1)～(3)所得的预测解与模型数值解对比结果如图7 所示。由图7 可见，在地表沉降的位移、沉降范围及沉降曲线轮廓上，预测解和模型数值解均取得了较好的一致性，验证了所提预测公式的准确性。

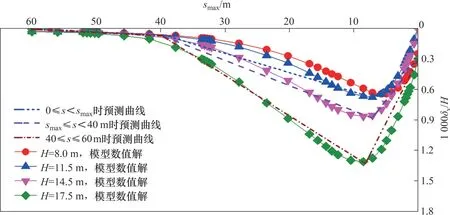
图7 不同开挖深度下的地表横向沉降预测解与模型数值解对比Fig. 7 Comparison of predictive solutions and numerical of ground surface transverse settlement for different excavation depths

3.3 纵向变形（平行基坑长边）分布规律

在距基坑外侧5、15、25 m处，当开挖深度为8.0、11.5、14.5、17.5 m时，坑外地表纵向沉降分布曲线如图8所示。由图8可见，与地表横向沉降发展规律类似，随基坑挖深增加，地表纵向沉降显著增大，这同样反映了基坑开挖的深度效应。此外，当基坑挖深一定时，地表纵向沉降从基坑端部向基坑中部逐渐增大而后趋于稳定，这是受基坑端部的“坑角效应”所致；同时，随着逐渐远离基坑端部，地表纵向沉降增大到最大并趋于稳定，表明基坑逐渐进入平面应变状态。然而，随着基坑挖深进一步增大，基坑变形进入平面应变状态的位置需要离基坑端部更远。为更清楚地解释上述现象，引入OU 等[24]提出的平面应变比(PSR)，其定义为基坑某断面的最大变形与该平面应变分析的变形最大值之比。当基坑变形符合平面应变时，平面应变比为1。平面应变比与基坑的多项特征相关，当基坑的“长深比”L/H超过一定值后，平面应变比即等于1，此时，基坑不是中部位置产生最大变形并进入平面应变状态，而是对处于基坑中部附近的一段区域都将处于平面应变状态。因此，当基坑挖深H逐渐增大时，为满足平面应变比为1，基坑中部进入平面应变状态的区域将逐渐减小。

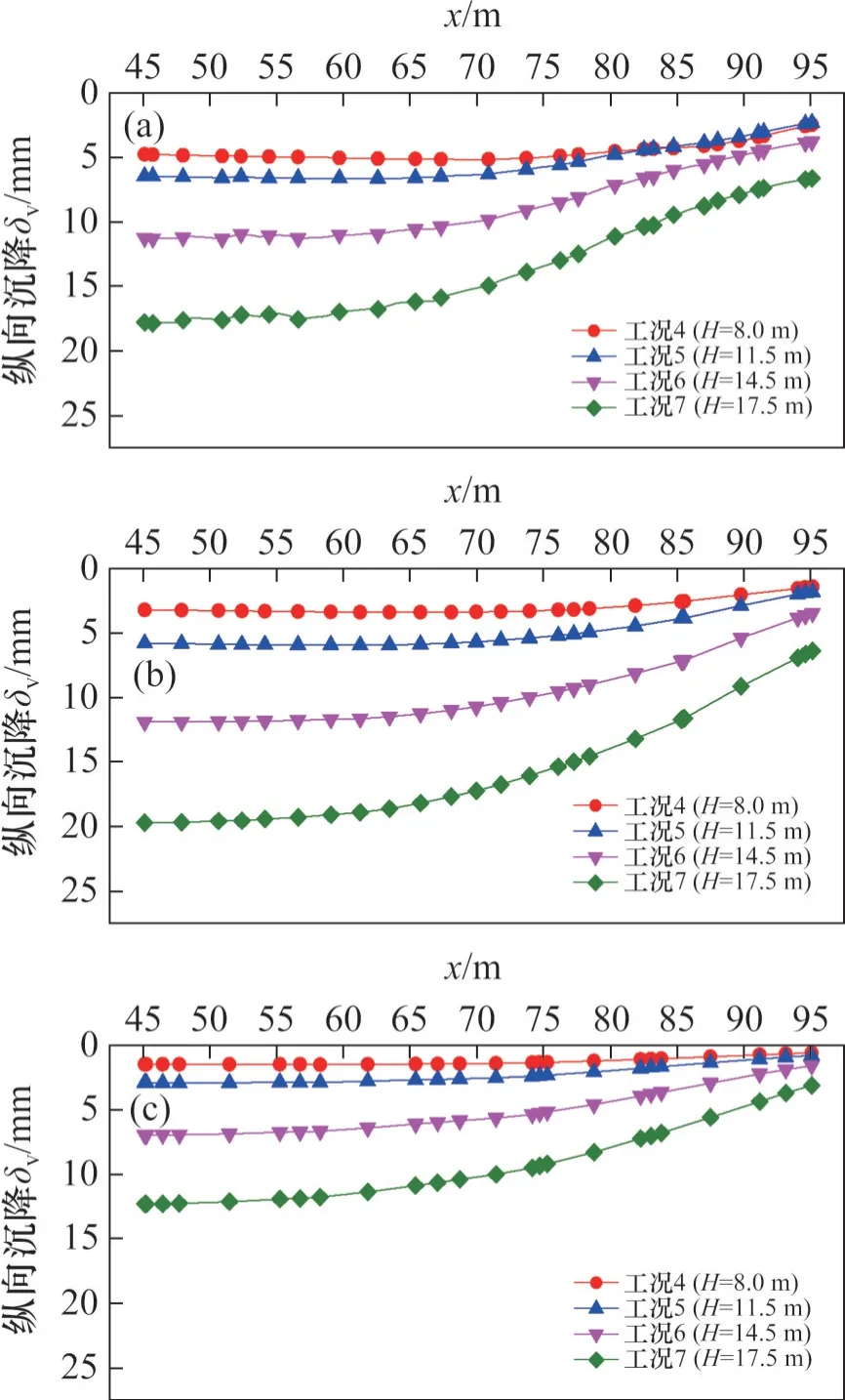
图8 不同开挖深度下地表纵向沉降Fig. 8 Curves of ground surface settlement longitudinal to wall during different excavation depths

3.4 纵向变形（平行基坑长边）分布预测及验证

在分析盾构掘进或基坑开挖等诱发邻近土体的相关变形时，常使用一些经典的轮廓函数来描述、分析开挖引起的变形形态。常见的轮廓函数是正态概率函数(正态高斯分布函数)，一些学者利用高斯函数描述隧道上方沉降槽的轮廓[25-28]。为探究芝加哥地区某基坑开挖的变形性状，ROBOSKI等[29]利用互补误差概率函数来描述基坑外侧平行于基坑围护结构方向的侧向地表沉降分布。目前对黏土地基中的开挖引起的地表沉降研究较多，而针对砂土地基中的基坑开挖的研究则非常少，RUSSO 等[30]研究意大利那不勒斯市区一火山碎屑砂中的27 m的深基坑时，对ROBOSKI等[29]所提预测公式进行了修正，使之能够由黏土地基进一步拓宽到砂土地基中的基坑开挖地表形态预测。

互补误差函数(erfc)定义为

其中：u为归一化高斯函数的归一化变量，erf(0)=0和erf(∞)=1。互补误差函数示意图如图9所示。

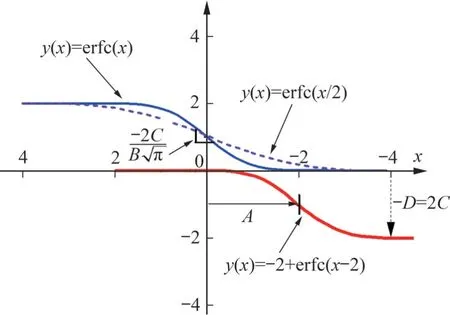
图9 互补误差函数示意图[29]Fig. 9 Diagram of complementary error function[29]

基于互补误差函数变形曲线的一般式如下：

式中：x为到原点的距离；A为互补误差函数拐点到基坑边角的距离，即δmax/2，B为拐点处斜率的形状参数；C为振幅参数；D为垂直偏移参数。坑外地表纵向沉降参数示意图如图10所示。

图10 坑外地表纵向沉降参数示意图Fig. 10 Schematic diagram of longitudinal settlement parameters outside pit

根据互补误差函数形态与开挖诱发的地表沉降分布关系可知：

式中：δmax为地表最大沉降值。

对于常规基坑开挖，分析侧的长度为L，不难发现基坑中间位置所在之处，即δmax在距离边角L/2位置，y(x=L/2)=D，代入式(5)得

当x增大到无穷大时，互补误差函数趋于零，必须进行合理截断来计算函数。GILL 等[31]基于最小二乘拟合发现当互补误差函数近似为零时，可取如下条件：

结合式(6)～(9)，式(5)可进一步写成：

由式(10)可见，仅需得到A和δmax即可得到变形曲线的控制方程。值得注意的是，对应不同的基坑开挖深度，显然也对应着不同的沉降曲线拐点即不同的A。ROBOSKI 等[29]对其实测基坑数据进行反分析，建立了A与He/L的近似关系：

结合式(10)和式(11)，即可绕过反弯点A，利用基坑挖深H、基坑长度L和最大沉降δmax这3 个控制参数给出基坑不同开挖阶段的坑外地表侧向沉降曲线。然而，式(11)是在芝加哥地区某基坑的实测数据基础上建立的，对于分布有深厚软黏土的杭州而言并不适用。因此，必须有针对性地建立起杭州地区基坑开挖坑外侧向沉降曲线的A与H/L的关系式。根据标准化有限元三维基坑模型各开挖阶段坑外沉降数据，杭州地区的2A/L与H/L关系如图11所示。

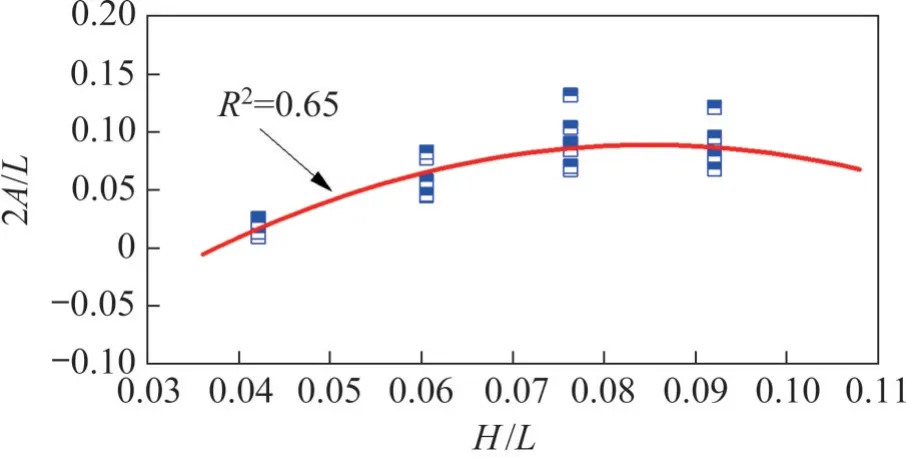
图11 2A/L与H/L关系曲线Fig. 11 Relationship curve between 2A/L and H/L

A与H/L的关系式为

结合式(10)和式(12)，可得考虑基坑各开挖阶段的坑外地表纵向沉降分布曲线如下：

在不同开挖深度以及间距下，本文的地表纵向沉降预测解与模型数值解对比结果如图12所示。由图12 可见，在沉降曲线上，尽管预测解与数值解存在一定差别，但地表最大沉降量及沉降曲线轮廓均吻合较好，且误差也在工程实践可接受范围内。由此，通过与不同开挖阶段、不同间距下的地表沉降曲线等对比，可验证所提预测公式的准确性。

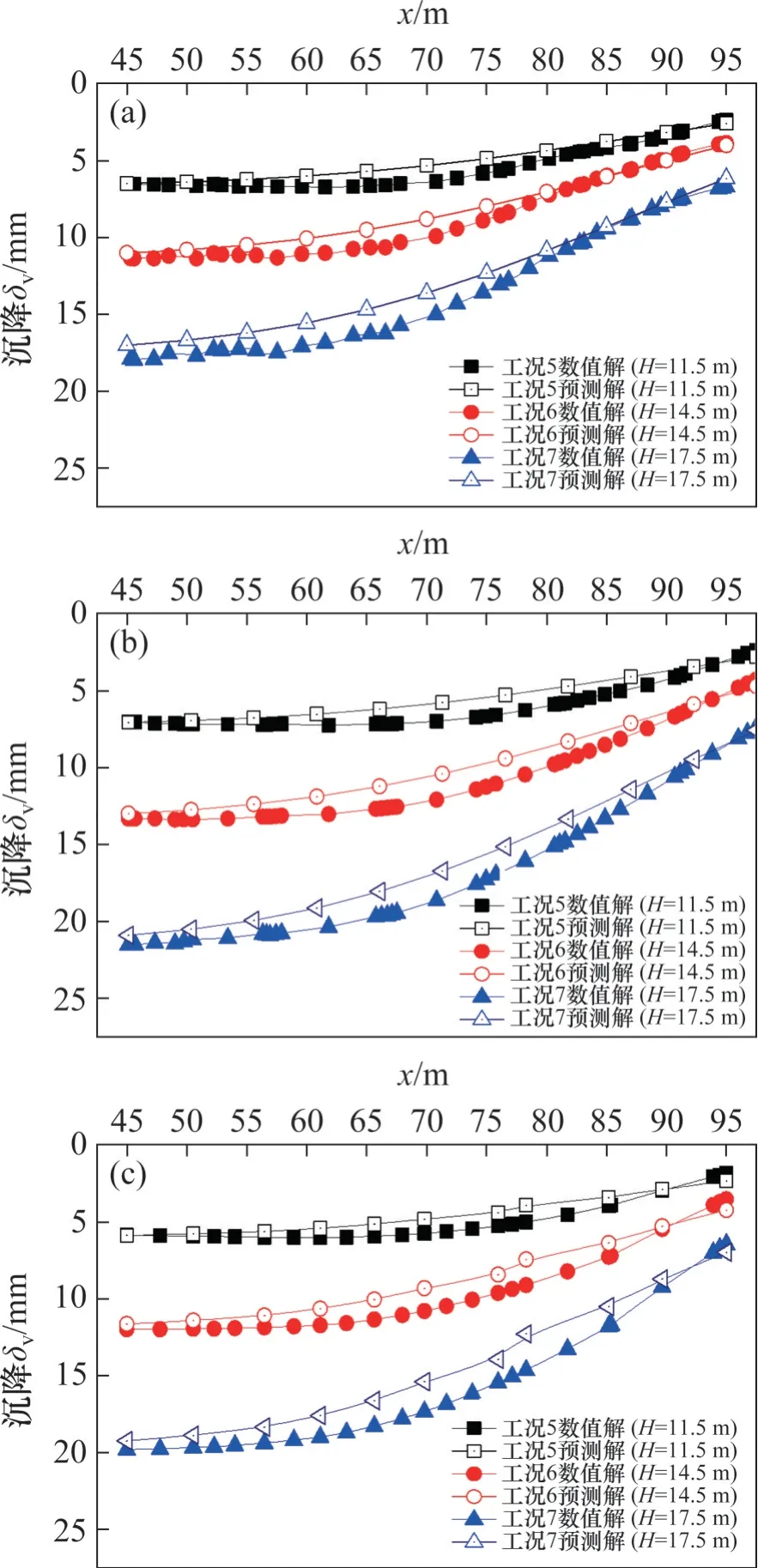
图12 不同开挖深度以及间距下的地表纵向沉降对比Fig. 12 Comparison of ground surface longitudinal settlement for different excavation depths

3.5 考虑开挖过程的坑外地表沉降分布预测流程构建

在任意开挖阶段(H)，坑外任意点的沉降值计算步骤如下：

1) 由式(1)～(2)计算基坑横向最大沉降值δmax以及所在位置smax(垂直基坑长边方向），代入式(3)即可得出坑外最大横向沉降分布曲线。

2) 利用δmax，由式(13)计算出过该横向最大沉降点的纵向(平行基坑长边方向)沉降分布曲线。

3) 当步骤2)中取坑外最大横向曲线上任意点时，也可得到对应的δ，将δ作为最大沉降代入式(13)，同样可获得过该点的纵向沉降分布曲线。

4 与工程实例结果对比

为进一步说明本文方法的合理性与适用性，选取杭州城东地区某地铁基坑为研究对象，基坑相关参数与上述标准化基坑模型一致性较好。场地土层参数以及基坑施工工况见表2 和表3，基坑几何尺寸以及地表沉降监测点布置简图如图13 所示。其中，基坑全长270 m。地表布置有A-A、B-B共2条监测线，线上各监测点距基坑长边的距离分别为3、6、10、18 m。基坑典型剖面以及各支撑情况如图13(b)所示。

图13 基坑平面及典型剖面示意简图Fig. 13 Schematic diagram of foundation pit plan and typical section

在不同开挖深度下，地表横向沉降预测解与现场实测结果对比如图14所示。由图14可见，虽然在基坑挖深较浅时，预测解与实测值存在一定差异，但整体而言，各监测点沉降及其变化趋势与本文所提预测结果基本一致，且随基坑开挖深度的增加，预测解和实测值的一致性更好。选取图14 中距基坑侧壁距离s=10 m 处(最大沉降位置)的沉降预测值作为最大沉降δmax代入式(13)，可得出基坑不同挖深下的地表纵向沉降预测解，如图15 所示。可见：尽管地表纵向沉降监测点较少，但在不同挖深下，地表纵向沉降与预测值较吻合。

图14 不同开挖深度下的地表横向沉降对比Fig. 14 Comparison of surface transverse settlement for different excavation depths

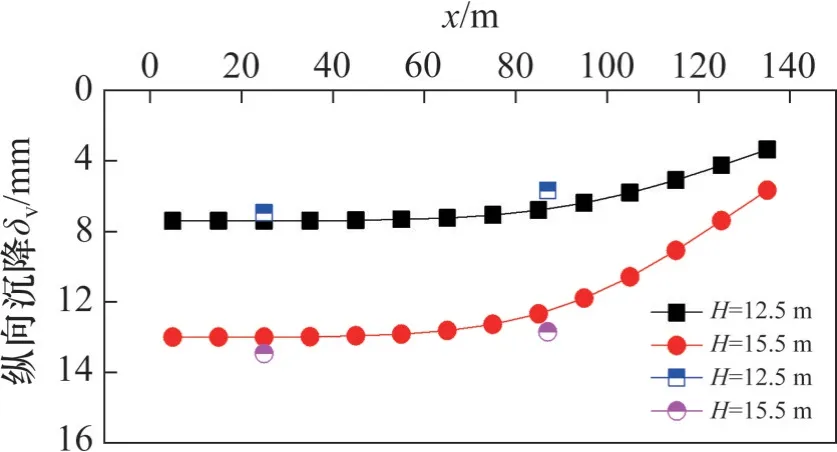
图15 不同开挖深度下地表纵向沉降对比Fig. 15 Comparison of surface longitudinal settlement for different excavation depths

以上结果进一步证明本文所提出的预测公式的适用性。本文所提出的预测公式作为一种简化实用计算公式，可对基坑开挖诱发的坑外地表沉降预测进行快速且简便预测。

5 结论

1) 基于所收集的16 个杭州地铁基坑案例，建立杭州地铁基坑标准模型，包括基坑几何参数模型、基坑施工过程模型以及场地土层参数模型。

2) 对所建立的杭州地铁基坑标准模型进行建模分析，通过将数值解与工程案例的实测结果、既有文献解进行对比，验证了所建标准基坑模型的准确性。

3) 以此数值模型为基础，分析地铁基坑在各开挖阶段的地表沉降特征。当开挖深度超过7 m时，坑外地表横向沉降曲线由“悬臂状”转化为“三段式”折线。随着挖深的增加，地表沉降显著增大，地表最大沉降的位置距基坑的距离也逐渐增大。基坑开挖的地表沉降影响范围近似为基坑最终挖深的3倍。

4) 提出可考虑基坑全过程开挖的坑外地表沉降分布的新预测方法，并验证了所提出方法的准确性。

5) 需要指出的是，本文所提出的动态预测方法主要针对杭州地铁基坑，对于其他地区基坑以及不同类型的基坑，该预测方法的适用性有待进一步验证，但是该预测方法的建立思路及方法对于其他不同地区不同类型的基坑分析仍然是适用的。