基于激光测距技术的灌浆流量检测方法测量精度研究
徐蒙,费章辉,刘磊磊,李晋峰,徐力生
(1. 中南大学 有色金属成矿预测与地质环境监测教育部重点实验室,湖南 长沙,410083;2. 中南大学 地球科学与信息物理学院,湖南 长沙,410083;3. 湖南省有色金属资源与地质灾害探查重点实验室,湖南 长沙,410083;4. 中铁上海设计院集团有限公司,上海,200070)
水电作为清洁、优质、可再生能源在我国能源体系中具有重要作用,水电开发是中国能源转型升级、实现“碳达峰”和“碳中和”目标不可缺少的重要保障[1]。灌浆因其有效性和经济性,是水利大坝基础加固、防渗、堵漏施工中必不可少的技术手段,但灌浆工程是隐蔽工程,其施工质量和灌浆效果难以进行直观检查,常常要求对施工过程参数进行检测和控制。
准确检测灌浆流量有助于精确计算耗灰量,确保灌浆效果[2-3],同时有助于工程师准确分析和判断地层状况,并指导下一步施工和设计,此外,灌浆量还关系到工程的经济效益,耗灰量异常将增大灌浆成本[4]。目前,电磁流量计被广泛应用于灌浆工程检测[5-7],但其在实际工程中对低流速状态的固液二相流测量误差很大,不能很好地满足灌浆工程动态检测浆液流量的要求。电磁流量计的正常测量流速范围为0.3~11.0 m/s,随着流速减小,测量误差以近似呈指数的形式增大,当流速在0.02 m/s 以下时,测量误差高达20%[8]。然而,屏浆阶段浆液长时间处于低流速状态,规范SL/T 62—2020 规定灌浆结束条件为[9]:灌浆段在最大设计压力且注入率降低至小于或等于1 L/min时屏浆30 min,且屏浆期间平均注入率不大于1 L/min。灌浆工程中多采用直径为40 mm 的钻杆作为注浆管道,当灌浆流量低至1 L/min 时,对应浆液流速约为0.013 m/s,在如此低的流速下,电磁流量计的测量误差将严重影响屏浆阶段流量参数的测量精度。
为了提高低流速状态下电磁流量计的测量精度,牛滨等[10]通过试验得出可以利用窄带滤波信号处理技术,扩大电磁流量计将所能检测的流量下限,从而满足对小流量、微流量的检测需求,但检测对象流速范围为0.02~0.20 m/s,明显高于屏浆阶段浆液流速,且灌浆现场环境恶劣,不可避免地对信号处理产生影响。刘林阴等[11]设计了一种基于DSP 的高频励磁电磁流量计,可显著提高低流速阶段测量准确度,但其研究的低流速仍高达1.00 m/s,远高于灌浆工程屏浆阶段浆液流速。GE 等[12]基于理论研究设计了新型电磁流量测量系统,通过搭建电磁流量检测测试平台进行试验研究,结果表明基于相关理论的电磁流量测量系统不仅能够满足传统流量测量的要求,而且在抑制外部强噪声干扰、提高小流量测量精度等方面具有独特的优势,但该研究仅限于室内试验,且所针对的低流量远高于灌浆工程屏浆阶段的1 L/min。综上所述,尽管电磁流量计在低流速状态下的测量精度不断提高,但针对屏浆阶段0.013 m/s 浆液流速,灌浆流量的测量误差仍然很大,同时,电磁流量计属于接触式仪表,在流量检测过程中直接与水泥浆液接触,易受流体性质的影响,特别是在小流速下水泥浆液易沉淀结垢,也会对电磁流量计的测量精度造成干扰。由此可见,目前检测方法和设备极大制约了灌浆技术的发展,提出全新的检测理论及方法对提高浆液流量测量精度具有重要的实际意义。
近年来,激光测距技术发展迅速,激光测距传感器具有测量检测速度快、检测精度高、测量误差小、抗干扰能力强等优点,可实现高精度的距离测量[13]。随着激光测距传感器精度不断提高[14-20],基于激光测距技术的液位测量系统也不断出现并广泛得到应用[21-24]。为此,本文作者基于激光测距技术,并结合搅浆桶的一体化结构设计,提出一种全新的浆液流量实时检测方法:通过激光测距传感器实时测量搅浆桶内液位的高度变化,根据液位高度变化与浆液瞬时流量转换关系,实现浆液流量的连续动态检测。该流量检测方法能有效克服屏浆阶段电磁流量计测量误差大的缺陷,同时,整个测量过程为非接触式测量,消除了灌浆过程中水泥颗粒对流量计测量的影响,提高了流量的测量精度。
本文首先通过理论分析,推导出液位高度变化与浆液瞬时流量转换公式。然后,基于ANSYS Fluent软件,通过数值仿真试验对该流量检测方法的测量精度进行分析。最后,利用正交法开展浆液水灰比、搅拌桨转速、排浆速度(即管道内浆液流速)对测量误差的影响程度,并对测量误差进行深入分析,完善基于激光测距技术的灌浆流量检测方法。
1 检测原理
1.1 整体检测方案
检测原理示意图如图1所示。固定在支架上的激光测距传感器连续、高频地测量搅浆桶内浆液液面高度,所测数据通过数据线实时传输到数据采集处理控制系统进行处理,并通过推导的计算公式对流量进行计算,流量计算结果和流量-时间等曲线显示在数据采集处理控制系统显示屏上。流量计算步骤如下。
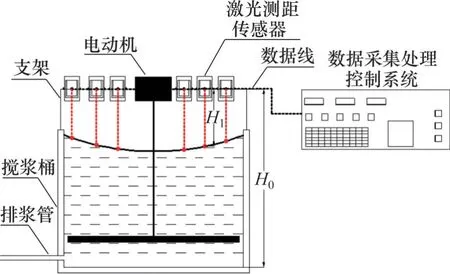
图1 基于激光测距技术的浆液流量测量方法原理示意图Fig. 1 Schematic diagram of the principle of slurry flow measurement method based on laser ranging technology
1) 液面高度换算。固定在搅浆桶上方的激光测距传感器到搅浆桶底部距离为H0,传感器所测固定点到液面的垂直距离为H1,则对应测量点液面高度为h1=H0-H1。
2) 液面函数拟合。以搅浆桶底部中心为原点建立直角坐标系xOy,各测量点坐标以(x,y)形式表示(其中,x为测量点距搅拌轴中心距离,y为测量点液面高度)。对各测量点液面高度进行拟合得到液面函数表达式为y(x)。
3) 流量计算。假设搅浆桶内浆液以搅拌轴为中心呈对称分布,根据旋转体体积积分公式得到搅浆桶内浆液体积为
式中:V为搅浆桶内浆液体积;r为搅拌轴半径;R为搅浆桶半径;y(x)为液面函数表达式。
对应时间段的流量为
式中:Qn+1是时间t为n+1 时的浆液流量;Vn和Vn+1分别是时间t为n和n+1 时的浆桶内浆液体积;Δt为两连续时间点的时间间隔。
1.2 浆液液面分布数学解
以搅浆桶底部中心为原点建立直角坐标系xOy,如图2 所示。搅拌桨旋转角速度为ω,选取液面上任一质量元dM,记为点A,其到搅拌轴轴线垂直距离为x(r<x<R),l为A点处液面的切线,l与水平线夹角为α。当液面搅拌稳定(即浆液绕着搅拌轴匀速转动)时,此质量元作匀速圆周运动,在竖直面上受到液面的支持力N和重力G的作用,二者的水平合力提供水平方向的向心力F,竖直合力提供浆液下降时的瞬时加速度a,支持力N的方向与水平线夹角为θ。
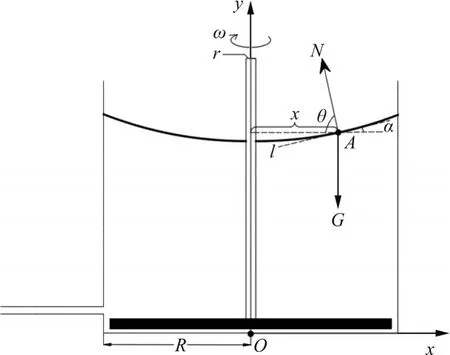
图2 浆液液面受力分析图Fig. 2 Stress analysis diagram of grout level
设浆液液面在直角坐标系xOy内的截线方程为y=y(x),对第一象限内的质量元dM进行受力分析,有
式中:G=gdM,F=ω2(x)xdM。有
式中:g为重力加速度;ω(x)为不同位置浆液旋转角速度。
液面处浆液流速不均匀,存在沿半径方向的速度梯度。当r<x<R时,以y轴为对称轴,任取圆柱面形状的液面元ΔS,设液面元ΔS与内外两侧
式中:F1和F2为两侧所受黏滞力;B为液面元ΔS的面积;μ0为浆液塑性黏度;τ0为屈服应力。在一定温度和压力下,μ0和τ0均为常数。
当液面搅拌稳定时,水平面内浆液作定常流动,此时,液面元ΔS所受内外液体施加的黏滞力相等,即
因此,沿半径方向速度梯度处处相等,即浆液流速沿半径方向按函数v(x)=kx+b分布,
式中:k和b为常数项。
由于浆液具有黏滞性,附着于固体壁上的流体与固体壁之间的相对速度为0,因此,ω(r)=ω,ω(R)=0,代入式(7)得
将式(9)代入式(4),得
假设同一时间点浆液液面各点竖向加速度近乎相等,a与x无关,对式(9)求积分,得y(x)在第一象限内的表达式为
式中:D为未知常数。
同理,当质量元dM位于第二象限内时,得y(x)在第二象限内的表达式为
综合式(10)和式(11),得y(x)表达式为
考虑函数拟合的简便性,对式(12)进行简化,得到浆液液面函数拟合表达式:
式中:f(x)为浆液液面函数拟合表达式;A、B、C和D均为未知常数。
根据各激光测距传感器所测液位高度数据,代入式(13),通过函数拟合求解得到A、B、C和D。
2 数学模型建立及求解
2.1 浆桶内浆液流动模型描述
2.1.1 模型建立
在灌浆工程中,常用搅浆桶直径为740 mm,高为500 mm。搅拌桨由搅拌轴和4 片桨叶组成,搅拌轴直径为20 mm,长为400 mm。桨叶直径接近搅浆桶直径。设置单片桨叶长度为300 mm,厚度为8 mm,高度为40 mm。搅拌桨底部距搅浆桶底部100 mm。灌浆工程中多采用直径为40 mm 的钻杆作为注浆管道。根据上述参数建立模型,如图3所示。
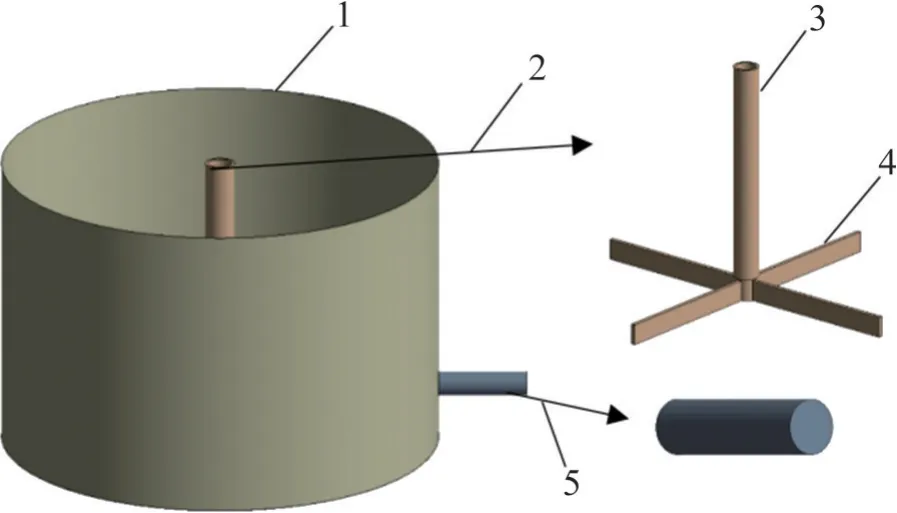
图3 搅浆桶模型结构图Fig. 3 Structure diagram of mixing bucket model
2.1.2 网格划分
利用DesignModeler模块中Slice功能将模型分解成搅拌桨、排浆管、桶壁共3个区块,并定义搅拌桨所在区域为旋转区域。设定物理场为CFD,采用MultiZone网格划分方法,定义搅拌桨区域网格尺寸为4 mm,排浆管和桶壁区域网格尺寸为5 mm,网格划分如图4 所示。整体模型网格数量为420 万个,网格偏度最低在0.840 以下,网格质量好。

图4 模型网格划分图Fig. 4 Meshing division of model
2.1.3 求解条件设置
灌浆工程采用多级水灰比配比的浆液,水灰比为3∶1~1∶1 的浆液在不同地层都得到了应用,不同水灰比配比下浆液参数如表1所示。
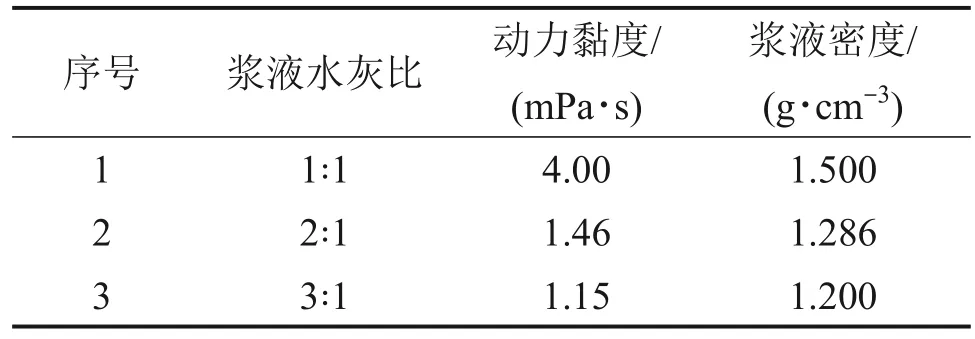
表1 不同浆液水灰比配比下浆液参数Table 1 Slurry parameters under different grout watercement ratios
由搅拌雷诺数计算式Re=nd2ρ/μ(其中,Re为雷诺数,n为叶轮转速,d为浆液直径,ρ为流体密度,μ为流体黏度)可知,在本搅拌模型下,浆桶内浆液流动状态为湍流,因此,选择k-ε标准湍流模型。搅拌不可压缩流体的流场可用下列方程组描述[25-26]。
1) 连续方程:
2) 动量守恒方程:
3) 湍动能k方程:
4) 湍动能耗散率ε方程:
式中:ux、uy、uz为相对速度分量;ui为沿i方向的速度分量(i=1、2、3);Fi为沿i方向的质量力;P为压力;v为流体运动黏性系数;K为湍动能;vt为涡黏性系数;ε为湍动能耗散率;Pr为湍动能生成率;σk=1.0;σε=1.3;Cμ、Cε1和Cε2均为经验常数;Cμ=0.09;Cε2=1.92;K为Von Kar-man常数。
将搅拌桨所在区域设为动区域,转速通过Cell Zone进行设置,模型采用瞬态计算方法求解。首先将出口边界类型设置为壁面,对浆桶内浆液搅拌至稳定,接着通过控制出口流量,使浆液沿着管路以一定速度流出。离散方程采用SIMPLEC算法求解。
2.1.4 网格无关性验证
以搅浆桶底部中心为原点建立空间直角坐标系xyz,其中排浆管方向为x轴方向,搅拌轴方向为y轴方向。为确定仿真模型网格数目,减少计算步骤和提高网格精度,设置排浆管出口边界类型为壁面,在搅浆桶内浆液初始高度为300 mm,浆液水灰比为1∶1,搅拌桨转速为40 r/min的条件下,采用2.1.3 节求解条件,控制搅拌时间为30 s,针对网格数目对搅拌后液面部分坐标点(x,z)液位高度y的影响进行研究,表2 所示为4 种网格数下液面部分坐标点液位高度。由表2可知:在相同试验条件下,随着网格数量增加,液面各点高度变化逐渐减小。当网格数量从420万个增加到760万个时,各点液面高度变化不明显,平均相对误差仅为0.1%,这表明液面高度计算结果基本不会随着网格的加密而发生改变。因此,在后续研究中,控制仿真模型的网格数量为420万个左右。
2.2 数值计算案例
本案例中,选取水灰比为1∶1的浆液作为试验材料。根据表1,设置浆液的初始密度为1.5 g/cm3,浆液黏度为4.00 mPa·s。在实际工程中,搅浆桶转速一般为30~40 r/min,本数值计算案例将搅浆桶转速设为35 r/min,桶内浆液初始高度设为300 mm。由于本研究主要针对低流速(小于0.3 m/s)下浆液流量测量精度,因此,控制出口浆液流速恒定为0.15 m/s,采用2.1 节中的模拟方法进行数值仿真。由于采用瞬态数值求解,计算要求更苛刻,计算量更大,因此,本计算案例中浆液流动时间控制为60 s。各时间点搅浆桶内浆液形态如图5和图6所示。

图5 各时间点浆液截面形态Fig. 5 Morphologies of slurry section at each time point

图6 各时间点浆液液面形态Fig. 6 Morphologies of slurry surface at each time point
从图5可知:随着排浆管处浆液流出,搅浆桶内浆液液面高度不断下降,在搅拌桨转动下,液面中心位置的浆液下陷形成漩涡。从图6可见:在排浆过程中,液面漩涡主要呈以搅拌轴为中心的对称分布。为了进一步探究排浆过程中液面高度的变化,在搅拌轴两侧同一直线上布置监控点16个,监控点初始坐标如表3所示,监控点布置如图7 所示。监控点实时反映各点液位高度y的变化。1~8号监控点的液位高度变化如图8所示。

表3 各监控点初始坐标Table 3 Initial coordinates of each monitoring point mm

图7 监控点布置图Fig. 7 Monitoring point layout plan
从图8可知:浆液流动初期,各监控点对应液位高度波动幅度较大,这是由于排浆管出口边界条件发生了改变,桶内浆液被瞬时赋予一定的流出速度,使得液面波动加剧。浆液流动20 s后的液位高度变化符合浆液正常流动时液面下降情况,因此,对浆液流动时间为20~60 s 时所对应的液位高度进行处理。以5 s 为间隔,选取20、25、30、35、40、45、50、55 和60 s 时16 个监控点的液位高度,绘制对应时间下液位高度散点图,并根据式(13)对各时间下浆液液面进行曲线拟合,得到各时间点浆液液面函数拟合表达式。
以20、30、40 和50 s 时16 个监控点的液位高度为例,利用Origin 软件绘制液位高度散点示意图,如图9所示,曲线拟合结果如图10所示。

图9 液位高度散点示意图Fig. 9 Diagram of liquid level scatter point
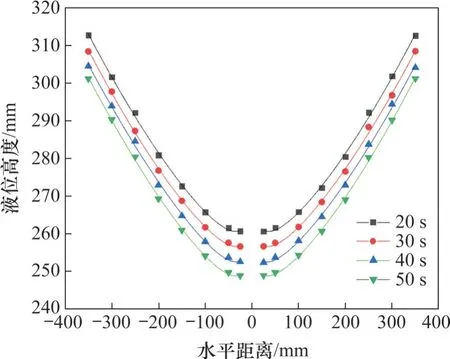
图10 液面拟合曲线示意图Fig. 10 Diagram of liquid level fitting curves
各时间下浆液液面函数拟合表达式如表4 所示。根据60 s 时液面函数拟合表达式,采用式(1)对排浆60 s后浆桶内剩余浆液体积进行积分求得拟合体积V拟合:
60 s后浆桶内实际体积V实际为
通过计算,60 s 后桶内实际体积为117.21 L,与数值仿真结果117.94 L接近,说明该数值方法是正确的。根据式(1)、式(2)与表4 计算浆液流量,结果如表5所示。

表5 不同时间段测量误差Table 5 Measurement error in different time periods
从表5 可以看出:以5 s 为单位计算浆液流量相对误差偏大,最大为4.42%,平均相对误差为1.77%;以10 s 为单位计算浆液流量整体相对误差较小,最大为2.83%,平均相对误差为1.26%。由于浆液是在0.15 m/s的低流速下流动,短时间内液面高度变化较小,使得液面波动所引起的液位高度测量误差被放大,导致相对误差较大。此外,浆液液面函数拟合与浆液体积积分也会带来不可避免的计算误差。整体而言,采用测量液面高度变化来得到低流速下浆液实时流量的检测方法具有一定可行性,测量相对误差在可接受范围内。考虑到在0.15 m/s排浆速度下,排浆10 s所对应搅浆桶内浆液液面高度下降约4 mm,建议选取桶内液面下降4 mm左右所需时间作为单位时间来计算浆液流量,以提高流量测量精度。
3 精度影响因素的正交化试验设计
3.1 正交化试验设计原理及策略
通过液面高度变化得到低流速下浆液实时流量的检测方法,该方法在测量精度方面易受灌浆材料、搅拌桨转速、排浆速度等因素的影响。水泥浆液材料的配比是影响浆液黏度和密度特性的主要因素,水灰比一般取3∶1、2∶1和1∶1,对应参数如表1所示,不考虑浆液黏度、密度的时变性,搅拌桨转速范围一般为30~40 r/min,取转速30、35和40 r/min,排浆速度取0.013、0.150和0.660 m/s。因此,针对水泥浆液配比、搅拌桨转速及排浆速度三因素开展三水平测试,探究不同因素对流量检测精度的影响。试验主要考虑多因素的主导作用,不考虑因素之间的相互影响,流量测量精度多因素水平如表6所示。
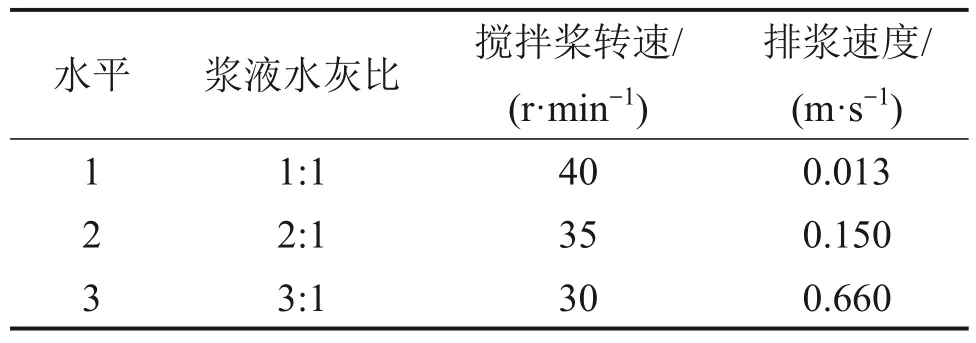
表6 流量测量精度多因素水平表Table 6 Multi-factor level table of measurement accuracy
根据正交表的正交性和均衡性设计要求,本试验采用L9(34)正交表进行试验设计,具体试验设计如表7 所示。通过表7 开展9 次数值仿真试验,模型建立与求解采用2.1 节和2.2 节中的方法,通过数值方法得到每种条件下的流量测量误差。
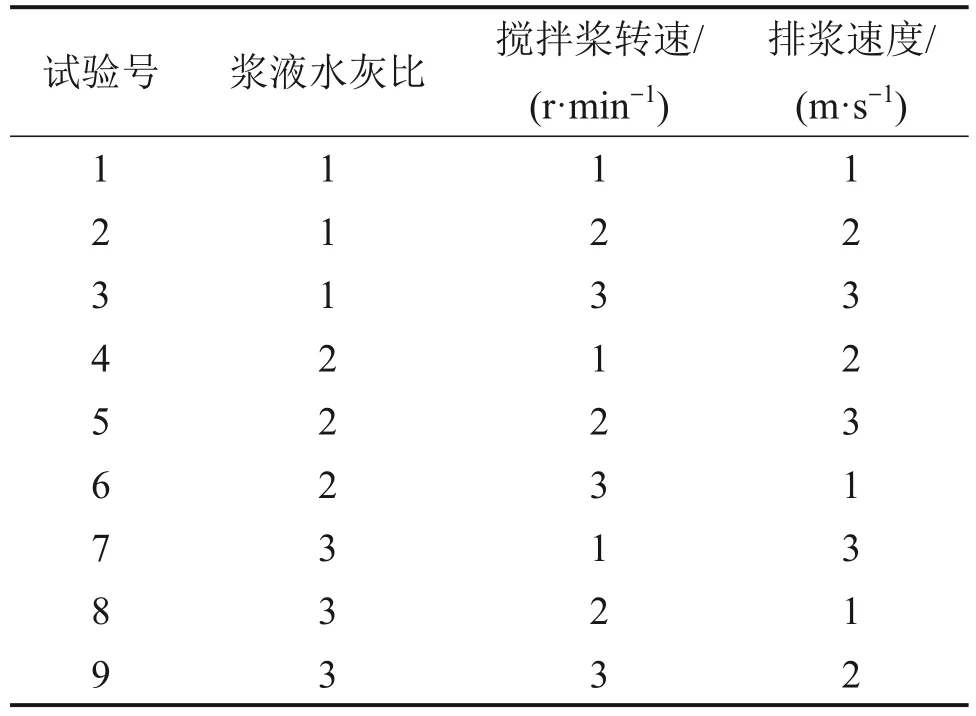
表7 流量测量精度正交试验表Table 7 Orthogonal test table for flow measurement accuracy
3.2 试验结果及分析
该试验的主要目的是测试上述9 种不同工况下,通过测量液面高度变化计算得到的流量与真实流量之间的误差,分析不同因素对该流量检测方法测量精度的影响。根据2.2节中结论,以桶内液面下降4 mm左右所需时间作为单位时间计算浆液流量,因此,0.660 m/s排浆速度下以2 s 为单位时间,0.150 m/s 排浆速度下以10 s 为单位时间,0.013 m/s排浆速度下以1 min为单位时间,并将计算流量与真实流量进行对比。
按照表7中试验号依次展开数值仿真试验,计算单位时间内的浆液流量,并与真实流量对比得出相对测量误差,同时,将各工况下多组相对测量误差取平均作为该工况下的平均相对测量误差,结果如表8所示。
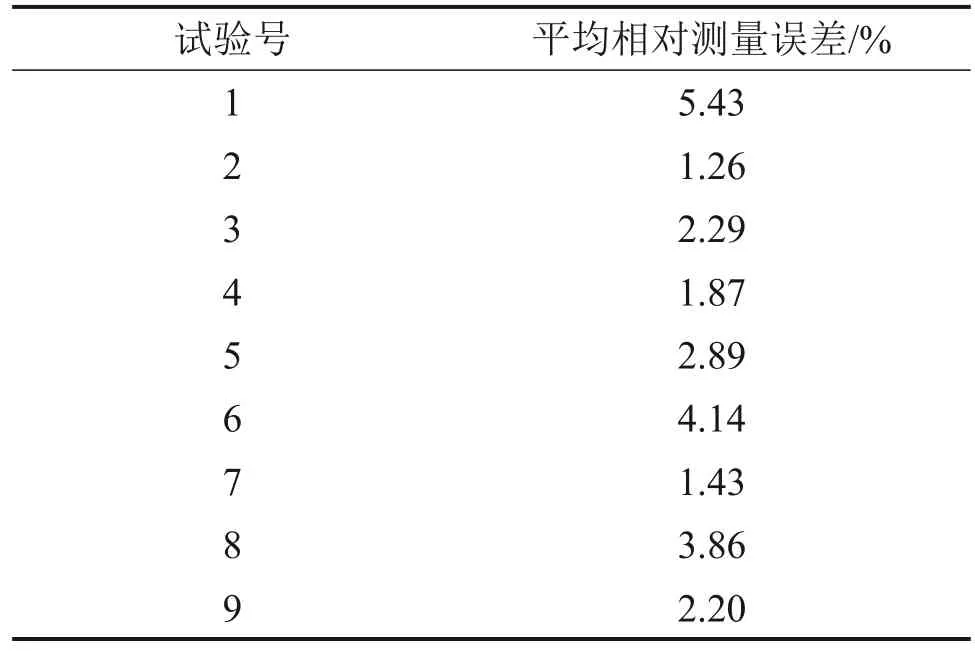
表8 各工况测量误差Table 8 Measurement error table for each working condition
由表8可知:各工况下浆液流量测量误差大部分在3%以内,1号、6号、8号试验的测量误差偏大,在3%~6%之间。为了分析各因素对流量测量误差的影响程度,按照直观分析法求取各因素各水平统计结果,各因素各水平值平均值为I1、I2和I3,极差为Rj。不同水平浆液水灰比、搅拌桨转速和排浆速度的试验分析结果如表9所示。
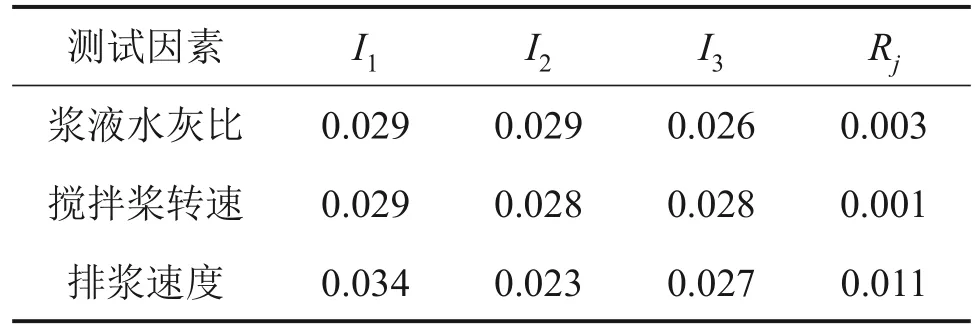
表9 各因素各水平统计表Table 9 Statistical table of various factors and levels
从表9可见影响测量误差的因素从大至小分别为排浆速度、浆液水灰比和搅拌桨转速,并且排浆速度的影响远大于其余两者的影响。1号、6号、8 号这3 组试验排浆速度均设置为0.013 m/s,流量测量误差远比其余6组试验的大,因此,对搅浆桶内浆液流场进行分析,探究0.013 m/s 低排浆速度下流量测量误差大的原因。
4 流量测量精度分析
4.1 低排浆速度下流量测量误差分析
为了分析低排浆速度下流量测量误差大的原因,利用Fluent 自带后处理软件得到搅浆桶内流场。图11 所示为上述9 组试验搅浆桶内浆液液面的速度云图,其中,图11(a)、(b)和(c)中排浆速度为0.013 m/s,图11(c)、(d)和(f)中排浆速度为0.150 m/s, 图11(g)、 (h) 和(i)中排浆速度为0.660 m/s。从图11 可以看出搅浆桶内浆液形态主要受排浆速度影响,水灰比、搅拌桨转速的影响较小,因此,选取1号试验、2号试验、3号试验为代表,分别对应排浆速度0.013、0.150 和0.660 m/s,绘制浆液液面速度矢量图,如图12 所示。从图12可知:在排浆速度为0.150 m/s 和0.660 m/s 时,浆液液面形成的切向流稳定,液面流速沿半径方向递增,形成以搅拌轴为中心的圆环状速度带,液面波动小;在排浆速度为0.013 m/s 时,浆桶内流场发生了剧烈变化,浆液液面形成的切向流不稳定,液面流速分布不均匀,形成多个低速区和高速区,影响了附近的流态分布,增大了液面的紊乱度,导致液面波动增大,不利于液位高度的准确测量。
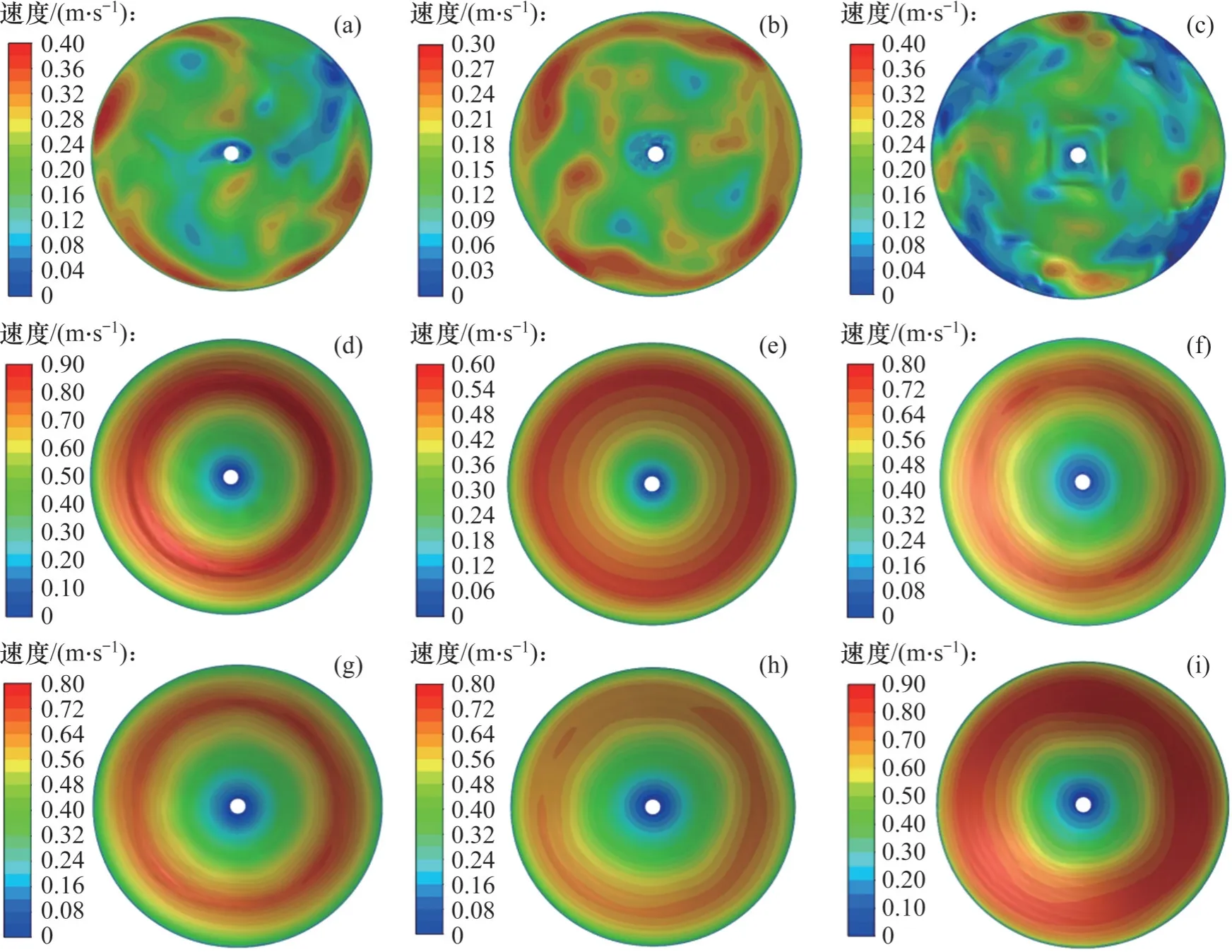
图11 浆液液面速度云图Fig. 11 Cloud diagrams of slurry surface velocity
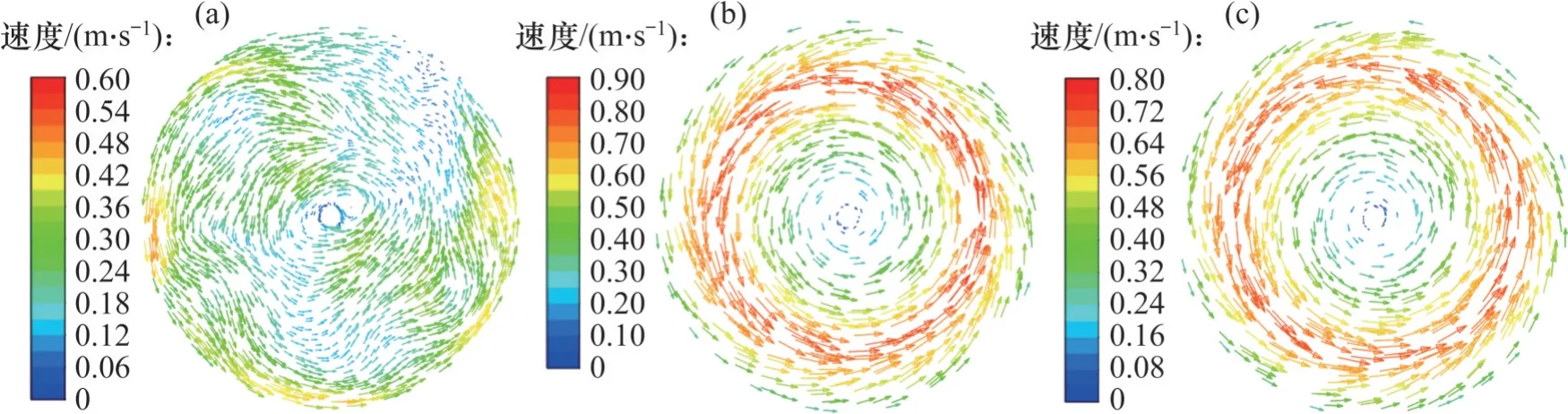
图12 浆液液面速度矢量图Fig. 12 Grout liquid surface velocity vectors
浆液液面的流态分布与浆液内部流场密切相关,图13 所示为1 号、2 号、3 号试验搅浆桶内浆液截面速度云图和速度矢量图,图14 所示为1 号试验浆液截面速度矢量细化图。从图13可以看出:在0.150 m/s 和0.660 m/s 排浆速度下,浆液截面流速以搅拌轴为中心呈对称分布,沿半径方向速度逐渐增大,浆液内部以轴向流和径向流为主,仅在两侧桶壁附近各形成1 个漩涡;而在0.013 m/s低排浆速度下,排浆管处浆液流出受阻,出现回流现象,增强了搅拌所产生的径向流和轴向流,而径向流和轴向流会促进液体混合,使搅浆桶内部流场变得混乱,在浆液内部形成多个漩涡。图14(b)、(c)和(d)中有较明显的3 处漩涡,这些漩涡起到混合搅动及悬浮的作用,导致搅浆桶内部浆液流速分布不均匀,进而加剧浆液液面不稳定。此外,在0.013 m/s 排浆速度下,排浆管处浆液流出速度很小,单位时间内搅浆桶内浆液液位高度变化较小,使得液面波动所引起的液位高度测量误差被放大,这也是导致0.013 m/s 低排浆速度下浆液流量测量误差偏大的一个重要原因。

图13 浆液截面速度云图和速度矢量图Fig. 13 Cross-section velocity cloud diagrams and velocity vector diagrams of grout
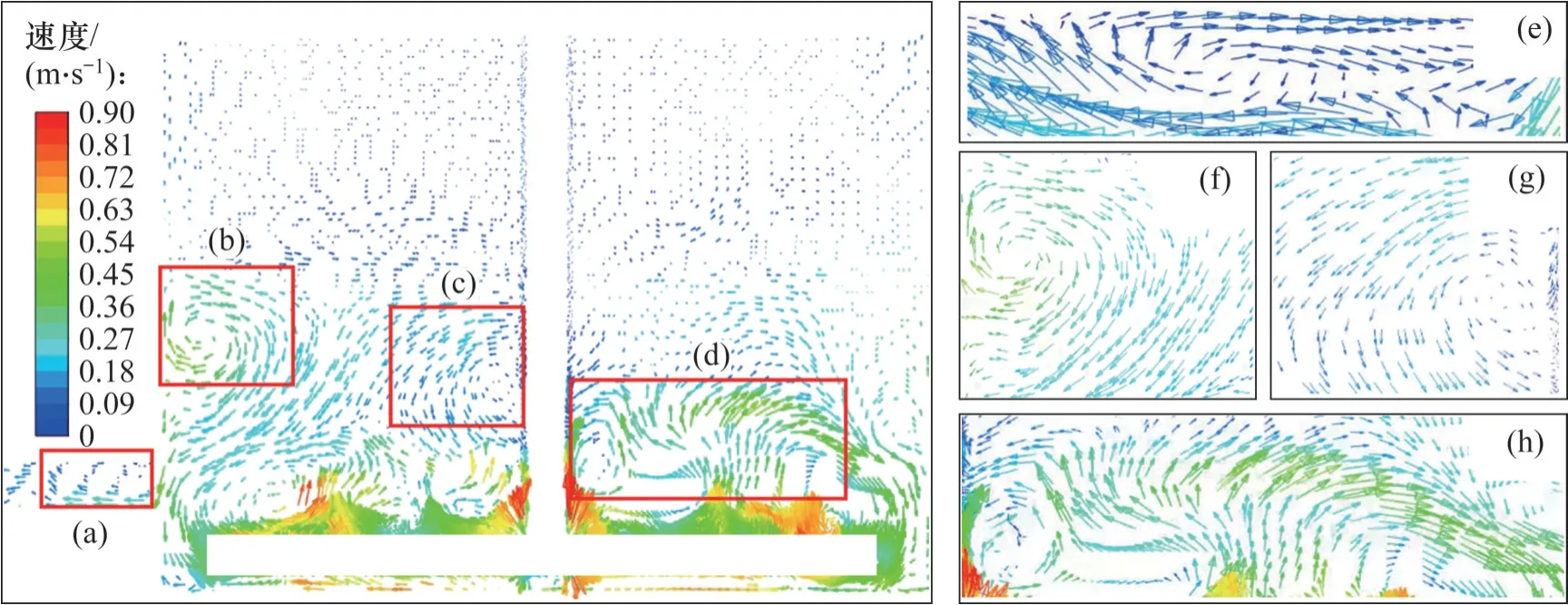
图14 1号试验浆液截面速度矢量细化图Fig. 14 Refinement diagram of cross-section velocity vector of No. 1 test slurry
4.2 电磁流量计的测量精度分析
为了进一步比较本文所提出的浆液流量检测方法所得测量精度与传统电磁流量计的测量精度,将1 号、6 号、8 号试验流量测量误差取平均值作为0.013 m/s 排浆速度下流量测量误差,将2 号、4号、9号试验流量测量误差取平均值作为0.150 m/s排浆速度下流量测量误差,将3 号、5 号、7 号试验流量测量误差取平均值作为0.660 m/s 排浆速度下流量测量误差,经整理可得0.013、0.150 和0.660 m/s 排浆速度下基于激光测距技术的浆液流量检测方法所得流量测量误差分别为4.48%、1.78%和2.20%。0.013、0.150 和0.660 m/s 排浆速度下K300 型号电磁流量计流量测量误差分别为20.0%、2.0%和1.5%[8]。通过比较可知,在流速为0.150 m/s 和0.660 m/s 时,2种检测方法的测量精度相差不大,相对误差接近2%,而在流速为0.013 m/s时,基于激光测距传感器的流量检测方法测量相对误差为4.48%,相较电磁流量计而言,测量精度大幅度提高。
5 结论
1) 推导了搅拌且排浆状态下搅浆桶内液面函数表达式,并基于此建立了搅浆桶液位高度变化与浆液流量间的转换公式。
2) 将搅浆桶内液面高度下降4 mm左右所需时间作为单位时间来计算浆液流量,相对误差在6%以内。在0.013 m/s 排浆速度下,基于激光测距技术的流量检测方法测量精度较电磁流量计而言有大幅度提高。
3) 通过正交试验极差分析,排浆速度、浆液水灰比、搅拌桨转速是影响流量测量精度的3个因素,其中,排浆速度的极差最大为0.011,这表明排浆速度是影响流量测量精度的最直接因素。
4) 在0.013 m/s 低排浆速度下,排浆管处浆液出现回流现象,致使浆液内部形成多个漩涡,加大了浆桶内部流场的紊乱程度,进而加剧了浆液液面的不稳定,导致流量测量误差偏大。

