球形破片空气阻力系数和飞行特性研究
刘建斌,郭德龙,任云燕,徐豫新,2,3,4,李旭东
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.高能量密度材料教育部重点实验室,北京 100081;3.北京理工大学 北京理工大学重庆创新中心,重庆 401120;4.北京理工大学 唐山研究院,河北,唐山 063000;5.中北大学 机电工程学院,山西,太原 030051)
破片式战斗部主要是在高能炸药爆炸作用下形 成大量高速破片,利用破片的高速撞击、引燃和引爆作用毁伤目标[1].在实战中,破片通常在空气中飞行一段距离后与目标交会,由于空气阻力的作用,破片飞行速度会逐渐减小.因此,在评估破片式战斗部实战威力时,通常会考虑破片的速度衰减因素[2−7],GJB2425-95 中给出了破片阻力系数的测试要求[8].球形破片因具有气动性能优越、空气阻力系数小等优点,被广泛运用于预制破片战斗部,且在空气中不发生翻转,易于在方法层面进行空气阻力系数特性研究,在此采用弹道枪对球形破片进行空气阻力系数特性研究,可为后续其他形状破片的阻力系数特性研究提供技术支撑.
目前国内外对球形破片的阻力系数特性早已开展了研究.例如,CHARTES 等[9]和王儒策等[10](1945)通过试验研究了ϕ9/16 in(ϕ14.3 mm)球形破片飞行马赫数在0.29~3.96 范围内空气阻力系数变化规律,分析了超音速下激波离体位置与马赫数关系,获得不同马赫数区间下的空气阻力系数.HENDERSON[11](1976)研究了球体的阻力系数与马赫数、雷诺数、球的温度和大气温度之间的函数关系,并给出了函数模型.谭多望等[12−15](2002、2007、2008、2011)通过二级氢气炮发射和静爆试验方法测量了不同材料、不同尺寸的锆珠、钢珠和钨珠的速度随飞行距离的衰减情况,结果表明:对于理想球形钨合金破片,在同一初始速度条件下,衰减系数为常数,空气阻力系数与初始速度有关,两者成线性关系.黄德雨等[16](2011)对低密度非金属球形破片在长距离飞行下的速度衰减规律进行了研究,结果表明破片在低速长距离飞行时的空气阻力系数与马赫数相关.ALLEN[17](2018)在CHARTES 和THOMAS 数据基础上基于量纲分析建立了球形破片飞行马赫数在0.2~2.0 区间下存余马赫数与飞行距离之间的函数关系式.此外,庞忠根[18](2009)、张华丽[19](2015)、李丽萍[20](2016)通过针对特定尺寸钨球速度衰减规律进行了试验研究并拟合了存余马赫数与飞行距离函数关系式,适用马赫数区间为3.0~6.0.综上所述可见,球形破片空气阻力系数研究仍十分活跃,目前对于球形破片空气阻力系数研究通常通过试验获得,一般认为破片速度与阻力系数呈现先增后减趋势,峰值点出现在马赫数1.4 左右.在亚音速至高超音速速度区间内,空气阻力系数、空气阻力随马赫数变化规律尚无系统研究,飞行距离、初始马赫数和存余马赫数三者间函数模型在工程上常用转换现有模型实现,阻力系数近似于常数,难于应用于初速2 000 m/s 以内的速度衰减效应计算以及爆炸安全领域的安全距离计算.
通过试验与数值模拟相结合的方式获得球形破片在飞行速度为6.0 马赫数以内的空气阻力系数和空气阻力随马赫数的变化规律,并在此基础上建立了球形破片飞行距离计算模型.相关研究成果可为球形预制破片战斗部威力场模型构建,毁伤效能评估以及爆炸安全领域的安全距离计算提供支撑,也可为其他类型破片空气阻力系数特性的研究提供方法借鉴.
1 破片速度测试试验
1.1 假设条件
首先,建立以下假设条件:
①试验测得的平均速度表示该区间的中点位置速度.
②通过试验测得的速度在计算空气阻力系数过程中,空气阻力系数Cd为常数.
③空气阻力系数Cd对应的速度采用计算Cd值时的速度平均值表示.
1.2 破片速度测试方案及试验装置
试验所用的破片速度加载装置选用12.7 mm 口径滑膛弹道枪,测时仪为南京理工大学LNG202G-2型,测时精度为1 μs,量程为1 μs~99 999 s.图1 为试验装置示意图,包括弹道枪、破片、测速靶和测时仪,图2 为试验现场图,每发试验最多可测量4 组速度.根据测试仪器使用说明,断通靶相对通断靶具有更高的测试精度,为提高测试精度[18],测速靶选用铝箔断通靶(简称铝箔靶),试验过程中,破片依次穿过5 个铝箔靶,靶间距分别为l1~l4;t0时刻,破片穿过Ⅰ靶,测时仪开始计时,接着依次穿过Ⅱ、Ⅲ、Ⅳ、Ⅴ靶,测时仪分别记录穿过的时刻t1~t4,通过li/(ti−ti-1)计算得到破片穿过相邻的2 个测速靶区间的平均速度v1~v4.靶间距用卷尺测量,卷尺最小刻度为1 mm.
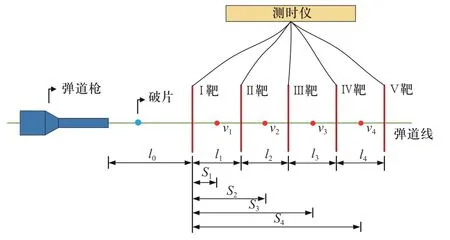
图1 破片速度测试装置示意图Fig.1 Schematic of test equipment

图2 破片速度测试实验现场图Fig.2 Layout of test site
破片速度衰减系数k由式(1)计算获得:
式中:Si为Ⅰ靶至第i个测速区间中心位置距离;n为测速区间个数;vi为球形破片经过第i个测速区间平均速度.空气阻力系数Cd可通过式Cd= 2km/(ρaS)计算获得,其中k为速衰减系数;ρa为当地空气密度;m为破片质量;S为破片迎风面积.
1.3 试验结果
试验测量的球形破片包括:ϕ6 mm 钢球、ϕ6 mm钨球、ϕ11 mm 钢球和ϕ11 mm 钨球,球形破片和弹托实物如图3 所示.空气阻力系数计算过程中,不同尺寸、材质的球形破片参数列于表1[21].试验共获得了23 组ϕ6 mm 和ϕ11 mm球形破片空气阻力系数列于表2,每组数据均由单枚破片测试获得.

表1 试验用球形破片参数Tab.1 Diameter and mass of fragments for tests

表2 球形破片空气阻力系数试验结果Tab.2 Test results of air resistance coefficient for fragments

图3 球形破片和弹托实物图Fig.3 Spherical fragments and sabots
将表2 中数据绘制成散点图如图4 所示.

图4 球形破片空气阻力系数试验结果Fig.4 Test result of air drag coefficient of spherical fragment
结合表2 和图4 可知,空气阻力系数与速度大小相关;在速度近似相同条件下,4 种不同尺寸或材质球形破片空气阻力系数试验结果未显著表现出与尺寸或材质相关.破片飞行马赫数从0.70 增大至1.05 时,空气阻力系数从0.59 增大至1.09,增大了约85%,可以看出球形破片飞行马赫数在接近1 时空气阻力系数急剧增大;马赫数大于3 时,空气阻力系数显现出随马赫数增大而减小的趋势.
2 数值模拟
2.1 模拟区域和网格划分
选用适用范围广、物理模型丰富、对网格要求不太高并且计算精度尚可的Fluent 进行计算,数值模拟区域形状为圆柱形,圆柱的高度为60D(D为球形破片直径),直径为30D,计算域尺寸设定如图5 所示.入流边界距离球心为20D,出流边界距球心位置为40D,球心距圆柱形计算域侧边界各为15D.网格由ICEM CFD 生成,近壁面边界层包含层流边界层和湍流边界层,通过计算不同马赫数下壁面函数yplus 值选取合适的第一层网格的高度,第二层网格的高度为第一层网格高度的1.2 倍,依次类推;通过数值模拟试算,第一层网格的高度与马赫数间的关系列于表3,网格类型为四面体非结构化网格.

表3 第一层网格高度Tab.3 Inner-layer grid size under different Mach numbers
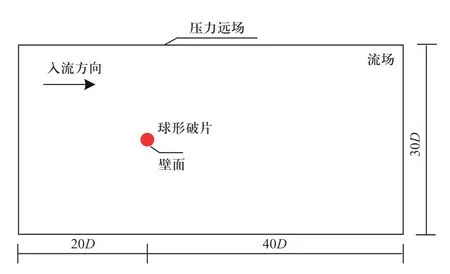
图5 模拟区域尺寸与边界设定示意图Fig.5 Schematic of calculation area size and boundary setting
2.2 求解器设置
求解器为Fluent 15.0,设置流场域四周为压力远场边界条件(pressure far field),用于模拟无穷远处的自由流条件;球形破片表面设置为壁面(wall),用于限定Fluid 和Solid 区域,如图5 所示;流体密度模型采用理想空气(ideal-gas),黏度模型采用经典的Sutherland 模型;对于湍流模型的选取,通过数值模拟试算对比了分别采用一方程模型Spalart-Allmaras(S-A)模型和二方程模型k-epsilon 模型和k-omega 模型的计算结果,结果表明在其他参数相同的条件下,S-A模型、k-epsilon 模型和k-omega 模型的计算结果相差不大,考虑到数值计算的效率,因此湍流模型选用S-A 模型.
2.3 数值模拟结果
分别对ϕ6 mm 和ϕ11 mm 球形破片建立数值模拟模型,获得2 种直径球形破片飞行马赫数小于6.0时的空气阻力系数数值模拟结果如图6 所示.选取部分马赫数下ϕ6 mm 和ϕ11 mm 球形破片空气阻力系数数值模拟结果列于表4.由图6 和表4 可见:①马赫数小于1.2 时,空气阻力系数逐渐增大;马赫数大于1.2 时,空气阻力系数逐渐减小;② 马赫数为0.7时,2 种直径球形破片阻力系数差值最大为−3.70%,可认为球形破片空气阻力系数与直径无关.

表4 2 种直径球形破片空气阻力系数数值模拟结果Tab.4 Typical numerical simulation results of air resistance coefficient

图6 2 种直径球形破片空气阻力系数数值模拟结果Fig.6 Comparison of air resistance coefficient for simulation results
表5 所示为空气阻力系数数值模拟与试验结果.
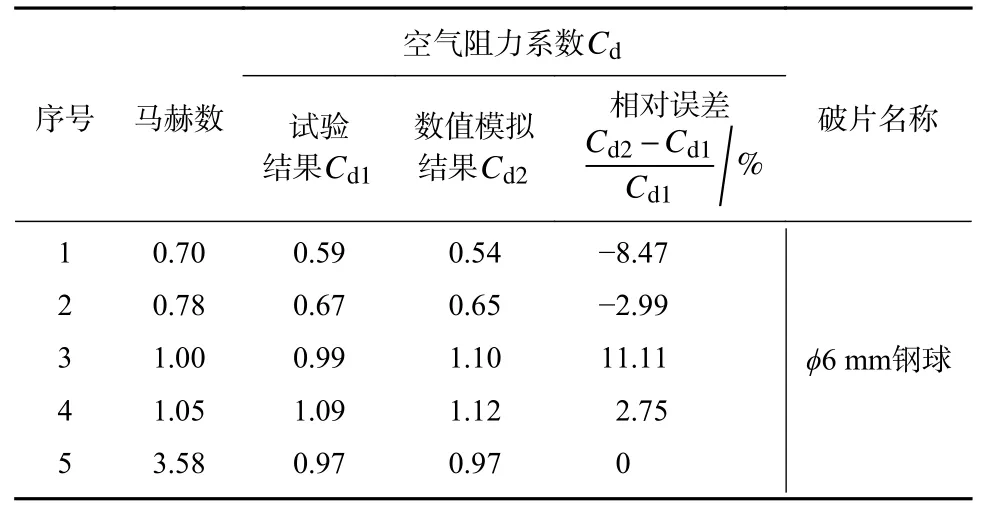
表5 试验与数值模拟结果对比Tab.5 Comparison of air resistance coefficient between test results and numerical simulation results
马赫数为1.00 时,数值模拟结果与试验结果相对误差最大,为11.11%;马赫数为0.70 时,数值模拟结果与试验结果相对误差最小,为−8.47%,误差范围未超过20%[21],但也说明在跨音速段,计算误差整体较大.
选取ϕ6 mm 球形破片空气阻力和流场静压云图数值模拟结果分别列于表6 和图7.
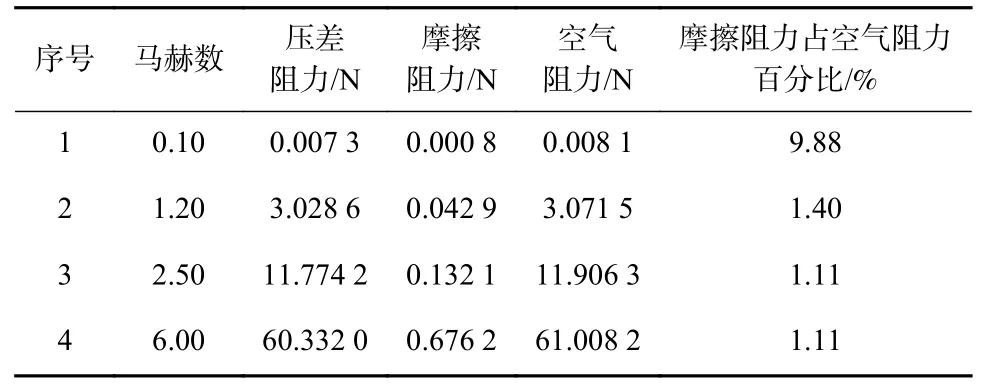
表6 ϕ6 mm 球形破片空气阻力数值模拟结果Tab.6 Numerical simulation results of air resistance for ϕ6 mm spherical fragment
从图7 中可以看出,当飞行马赫数为0.10 时,低压区(大气压为93 630 Pa)分布在球形破片的中部,随着马赫数增大,低压区向尾部聚集.结合表6 可见,空气阻力随马赫数的增大而增大,压差阻力占比总空气阻力达90%以上,摩擦阻力占总空气阻力比例10%以下.将ϕ6 mm 球形破片空气阻力数值模拟结果绘制成曲线如图8 所示.由图8 可见,空气阻力与马赫数近似呈二次方关系[19];在接近音速时,即马赫数在0.8 左右时空气阻力急剧增加.
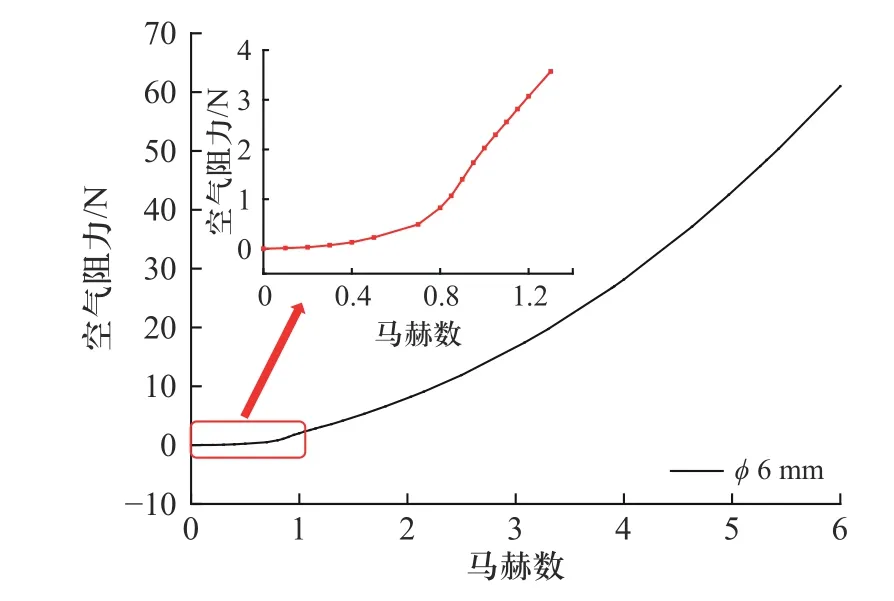
图8 ϕ6 mm 球形破片空气阻力数值模拟结果Fig.8 Numerical simulation results of air resistance for ϕ6 mm spherical fragment
3 结果与分析
3.1 空气阻力系数试验与数值模拟结果与分析
将试验与数值模拟获得的ϕ6 mm 和ϕ11 mm 形破片的空气阻力系数绘制成散点图和点线图,并与文献[10]中给出的球形破片空气阻力系数进行对比,如图9 所示.由图9 可见,破片飞行马赫数小于等于3.0 左右时,文献[10]中给出的结果显著偏小,大于3.0 左右时,数值模拟结果和文献[10]中数据较为一致.

图9 球形破片空气阻力系数对比Fig.9 Comparison of air resistance coefficient for test, reference and simulation results
对ϕ6 mm 球形破片空气阻力系数试验和数值模拟结果进行拟合,获得空气阻力系数与速度之间函数关系式,拟合结果如图10 所示.
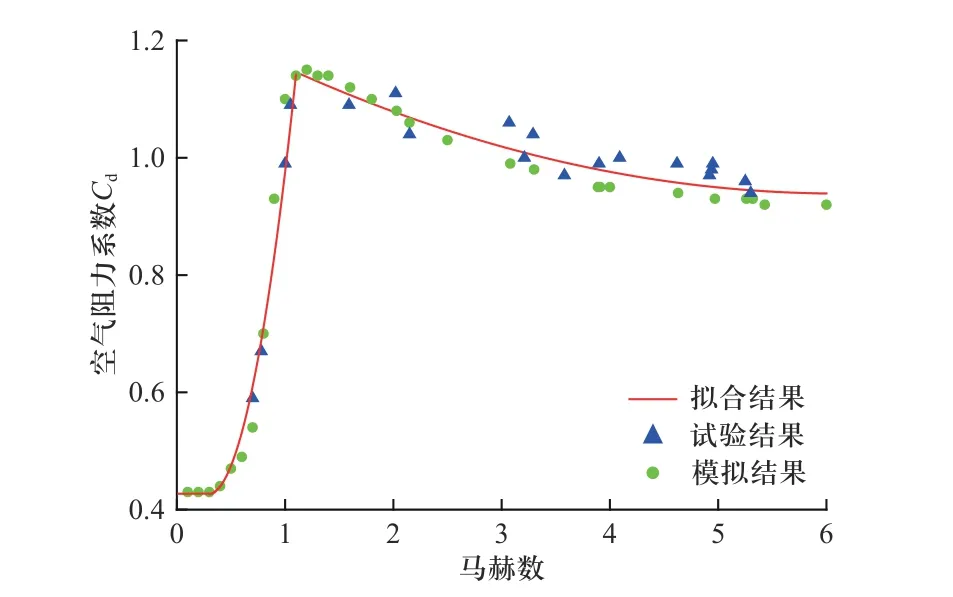
图10 ϕ6 mm 球形破片空气阻力系数拟合结果Fig.10 Fitting results of air resistance coefficient for ϕ6 mm spherical fragment
空气阻力系数与马赫数间函数关系式为
式中Ma为马赫数,
式中:v为破片飞行时的速度;vs为破片飞行时当地音速.
3.2 破片飞行距离计算模型
破片在空气中飞行时,空气阻力大小与速度的平方成正比[22],具体形式如式(4)所示,该式通常也被称之为阻力二次方定律.
式中:F为空气阻力;Cd为空气阻力系数,为量纲一量;ρa为当地空气密度;S为破片迎风面积;v为破片飞行速度.在忽略重力影响的情况下,式(4)可变换为
式中m为破片的质量.在式(5)的基础上,结合式(2)建立破片飞行距离x与初速v0和存速vx间函数模型.在过程中,对相关变量进行量纲一化,建立量纲一关系式[17].
首先,定义量纲一数z:
式中:D为球形破片的直径;ρp为破片密度;ρa为空气密度;x为破片飞行距离;kz为比例因子,与距离x单位相同.
对式(5)进行变换:
结合式(3):
球形破片质量m跟密度ρp、直径D之间存在如下关系式:
结合式(9)和(10),式(8)可变换成:
当Cd=A时,代入式(11):
当Cd=A+BMa+CMa2时,代入式(11):
式中:Ma0=v0/vs,Max=vx/vs,Max是指破片初始马赫数为Ma0时,飞行距离x后的存余马赫数;z0= 0;A、B、C为系数.
通过对式(12)和式(13)进行积分,结合式(6)可得空气阻力系数为常数和与马赫数成二次函数时的飞行距离x与初始马赫数Ma0、存余马赫数Max之间关系式:
选取试验数据和文献[12]中给出的两种材质的球形破片长距离飞行时的试验数据,对比建立的破片飞行距离计算模型计算结果分别列于表7 和表8.从表7 和表8 中可以看出,通过建立的飞行距离计算模型计算的结果与试验结果及文献[9]中给出的试验结果最大误差在3%左右.

表7 本文试验结果与模型计算结果对比Tab.7 Comparisons of flight distance between test data and calculation results of this model

表8 文献[12]试验结果结果与模型计算结果对比Tab.8 Comparisons of flight distance between references [12] test data and calculation results of this model
在战斗部动爆威力计算时,球形破片空气阻力系数通常取0.97[2−4];此外,王儒策等[10]也给出了不同速度区间球形破片空气阻力系数.对比球形破片初始马赫数为6.0,存余马赫数分别为3.0、1.1 和0.5时,采用0.97 及文献[10]中空气阻力系数和上述建立的飞行距离计算模型计算的飞行距离结果列于表9,计算过程中所需的破片参数及大气参数取表8 中钨球对应的参数.从表9 中可知,在初始马赫数取6.0条件下,当存余马赫数取3.0 时,空气阻力系数取0.97计算的飞行距离相比上述模型计算的结果偏大0.11%,近似相等,采用文献[10]中的空气阻力系数计算的飞行距离相比上述模型计算的结果偏大4.56%;当存余马赫数取1.1 时,空气阻力系数取0.97 计算的飞行距离相比上述模型计算的结果偏大6.85%,采用文献[10]中的空气阻力系数计算的飞行距离相比本文模型计算的结果偏大8.30%;当存余马赫数取0.5 时,空气阻力系数取0.97 计算的飞行距离相比上述模型计算的结果偏小10.58%,采用文献[10]中的空气阻力系数计算的飞行距离相比上述模型计算的结果大9.00%.

表9 破片飞行距离计算结果对比Tab.9 Comparisons of flight distance results for different models
4 结 论
通过对ϕ6 mm 和ϕ11 mm 2 种直径球形破片进行空气中运动阻力系数特性试验和数值模拟研究,获得了球形破片空气中飞行马赫数在6.0 内空气阻力及系数随速度的变化规律,结论如下:
①相同飞行速度下,不同直径球形破片空气阻力系数相同;球形破片的空气阻力系数随马赫数的增加先增大后减小,并非一恒定值,马赫数为1.2 时最大.
②球形破片空气阻力在马赫数为0.8 左右时急剧增加;其中,压差阻力占比90%以上,摩擦阻力占比10%以下.
③建立了球形破片空气阻力系数随马赫数变化的函数和球形破片飞行距离计算模型,具有较高的计算精度.

