基于改进SURF算法的无人机遥感图像配准
高 强, 魏利波
(沈阳大学 a. 科技创新研究院, b. 信息工程学院, 辽宁 沈阳 110044)
无人机导航技术一直是国内外研究的重点和热点,目前用无人机进行定位与导航通常是通过卫星导航系统和惯性导航系统来实现的。然而,卫星导航系统自主性能较差,也存在抗干扰能力较弱等问题[1];惯性导航系统的定位精度与其使用的惯性器件的精度紧密相关,很大程度上会受到使用成本的限制,并且导航误差的累积较为明显[2]。
随着对计算机视觉研究的深入以及图像处理技术的日渐成熟,使得视觉导航成为无人机导航研究的重要方向[3]。基于视觉的导航方法主要是无人机利用图像传感器获取目标区域的图像,与地图库中携带地理位置信息的基准图像进行匹配,通过图像配准来获得自身的位置信息,进而实现无人机的自主导航。图像配准算法在无人机视觉导航中起着关键的作用,配准效果将直接影响到无人机自主定位的精确程度[4]。因此对无人机遥感图像的配准方法进行研究能够更加促进无人机的应用和发展,具有很强的实践意义。
按照进行匹配所使用的图像信息的不同,图像的配准算法大体分为基于图像灰度信息、基于图像变换域和基于图像特征3种类型[5]。其中,基于图像特征的配准算法对于亮度不均匀、有尺度变化、存在旋转或者被遮挡的图像匹配误差更小,适合应用于会出现旋转、光照、尺度等变化的环境中,可以处理变换较为复杂的图像间的配准问题。基于点特征的图像配准算法因其稳定和高效的特点而更受研究者的青睐。其主要流程包括:图像特征点的提取、描述以及匹配[6]。
目前,基于点特征的图像配准算法主要有 SIFT算法[7-8]、SURF算法[9-11]、BRISK算法[12-13]以及ORB算法[14-15]等。其中,SURF算法[16]具有良好的旋转不变性、尺度不变性、抗噪性等特点,并且可以较快地提取特征点。但该方法的描述子维数高、所占计算资源较大,在特征描述阶段花费的时间较长。针对这个问题,本文将BRISK和SURF算法结合实现同时具备高速率和高精度的无人机遥感图像配准方法(SURF-BRISK)。
1 SURF算法
SURF算法利用盒式滤波器和积分图像,直接对积分图像进行加减运算,减小了计算的复杂度,提高了算法运行速度。
SURF算法的主要步骤如下。
1) 计算积分图像。构造积分图像是整个SURF算法流程中非常重要的一个环节,通过积分图像的使用,SURF算法降低了卷积运算的复杂度、加快了特征点检测速度。积分图像与原图像大小一致,积分图像中1个像素点(x,y)的灰度值是在原图像中从图像左上角像素点开始到该点止的、包含该点在内的矩形内的所有像素点灰度值的总和,计算过程如式(1):

(1)
式中:I(i,j)为原图像中像素点的灰度值;I∑(x,y)为积分图像中像素点(x,y)的灰度值。
2) 使用Hessian矩阵检测特征点。SURF算法检测图像特征点是通过Hessian矩阵实现的。检测到的特征点具有更高的准确性。Hessian矩阵由高斯函数的2阶微分组成,2元高斯函数G(x,y,σ)的定义如式(2):

(2)
在尺度σ上,将图像I中某一点(x,y)的Hessian矩阵定义如式(3):

(3)
式中,Lxx(x,y,σ)、Lxy(x,y,σ)、Lyy(x,y,σ)为高斯函数在点(x,y)处的2阶导数。
SURF算法采用盒状滤波器与图像进行卷积得到的结果Dxx、Dxy、Dyy代替高斯函数的2阶微分Lxx、Lxy、Lyy,则可以得到近似的Hessian矩阵行列式,如式(4):
Det(H)=DxxDyy-(ωDxy)2。
(4)
式中,ω为权重系数,是为了平衡因近似带来的误差和提高计算的效率而设置的,一般取ω=0.9。
3) 构造尺度空间。为了检测特征点检测算法的尺度不变性,要在不同的尺度空间中进行图像特征点的检测,所以需要构造尺度空间。SURF算法构造尺度空间的方法是使用不同尺寸的盒状滤波器对同一幅图像进行卷积。
SURF算法的尺度空间由若干层组成,每4层又构成1个组。在SURF算法中,最小尺度的盒状滤波器的尺寸为9×9,其他尺度空间的盒状滤波器的尺寸都是由9×9盒状滤波器扩展得到的,运算速度与盒状滤波器模板的尺寸大小无关。
4) 定位特征点。像素点经过Hessian矩阵处理后,需要与其3维邻域内的26个点进行大小比较,如图1所示,如果该点是这26个点中的最大值点,则将其作为初步确定的特征点。
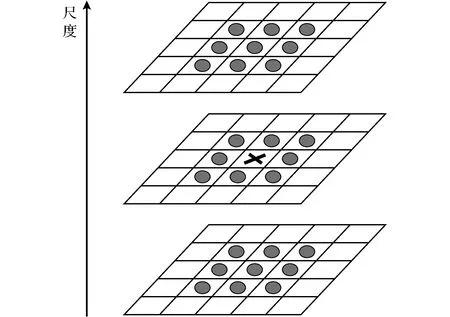
图1 尺度空间极值点检测Fig.1 Detection of extreme points in scale space
5) 确定特征点主方向。为保证算法的旋转不变性,需确定特征点的主方向。在SURF算法中,通过对特征点邻域内的Harr小波特征进行统计来确定特征点主方向,圆形邻域内模值最大的扇形指向即为特征点的唯一主方向。
6) 构造特征描述子。在特征点周围取1个正方形框,生成特征描述子时将正方形分割成16个子区域,每个子区域25个采样点。
2 SURF-BRISK算法
尽管SURF 描述子具有较强的图像配准适应性,但由于其具有较高的维数,故SURF运算占用的计算资源较大、效率较低。针对这一问题,本文提出利用BRISK二进制描述代替SURF描述子,以得到一种更高效的算子组合配准优化算法,从而实现快速和准确的图像配准过程。
SURF-BRISK算法框图如图2所示。
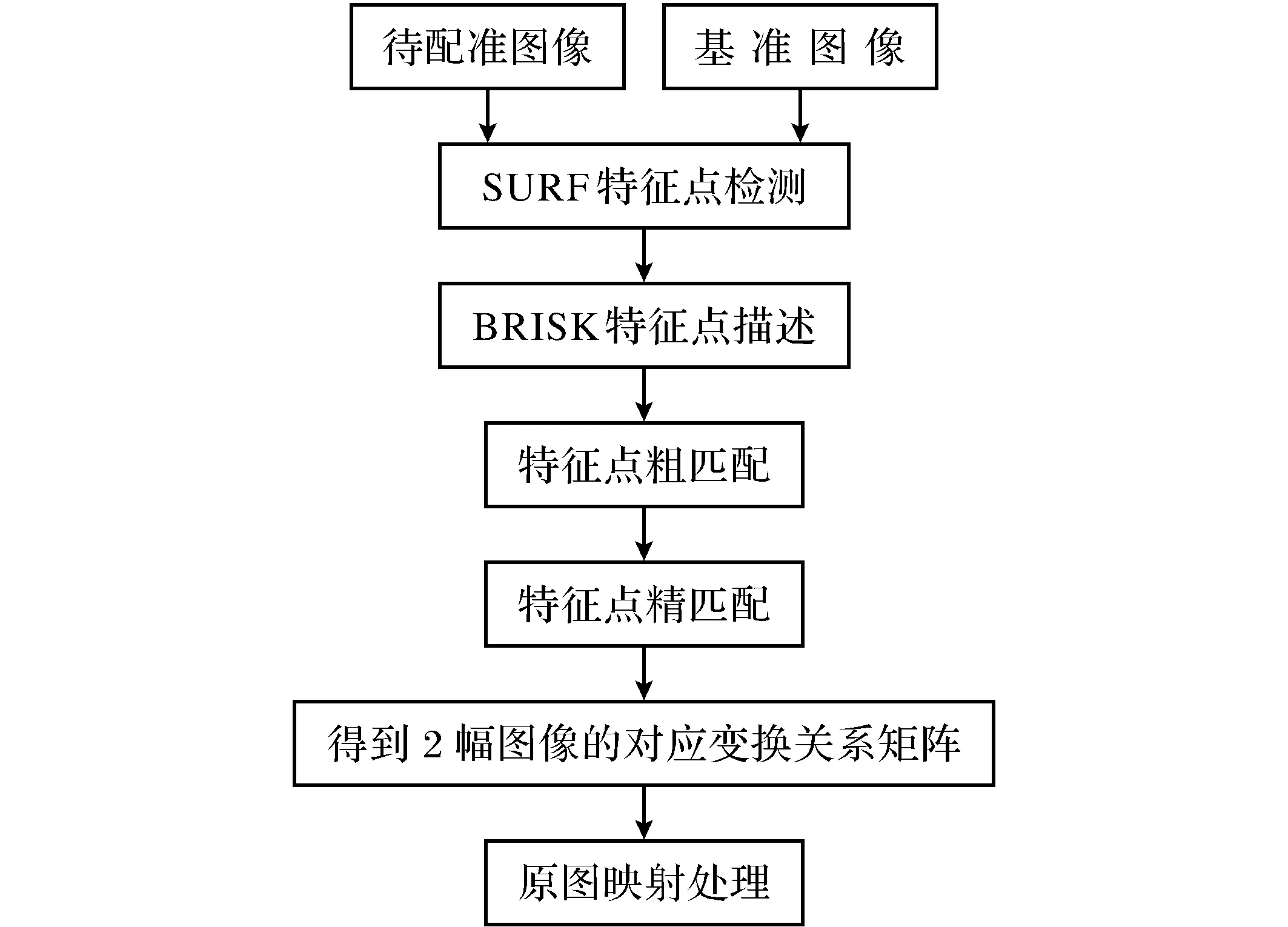
图2 SURF-BRISK算法框图Fig.2 Block diagram of SURF-BRIDGE algorithm
2.1 特征点检测与描述
1) 提取特征点。算法中的特征检测子是用来对图像特征进行提取的,检测到的特征点数量需要达到一定要求,同时冗余的特征点要尽可能的少。SURF作为特征检测子有较好的鲁棒性,可以更快速的获取到具有尺度不变性、旋转不变性以及抗噪性的特征点,且获取到的图像特征点较稳定。
2) 生成二值描述符。BRISK算子是1种二值算子,所占计算资源较小,以均匀采样模式进行特征点描述,生成描述符时间更短,具有更快的匹配速度。同时,BRISK描述子还具有良好的旋转、缩放不变性以及抗噪性。
2.2 特征匹配
在完成对待配准图像和基准图像的特征提取与描述后,需要对特征描述点进行匹配操作,从而获得相似特征点对。
作为1种常用的图像特征点匹配方法,FLANN可以对大数据集和高维特征进行快速最近邻搜索。该方法可以通过参数的调整以及阈值的设定来提高图像匹配的精度[17-18],具有较快的速度。因此,本文利用FLANN算法对无人机遥感图像进行特征点的粗匹配操作,得到待配准图像和基准图像的初始匹配点集。
2.3 特征匹配点优化
针对图像特征点的误匹配问题, 本文利用RANSAC算法[19-20]实现误匹配点的剔除。 RANSAC算法是1种常用的匹配点提纯方法, 主要是在待配准图像和基准图像的初始匹配点集中对误匹配特征点对进行筛选与剔除, 从而提高配准的精度。 其具有较好的鲁棒性, 可以在很大程度上优化匹配结果。
RANSAC算法采取的是采样与验证的策略,可以在包含误匹配点的数据集中,通过迭代寻找最优参数模型。其主要思路是求解单应性矩阵E。假设基准图像中的待匹配点坐标为(x,y),待配准图像中的待匹配点坐标为(x′,y′),则单应性矩阵E描述了图像之间的几何变换关系,如式(5):
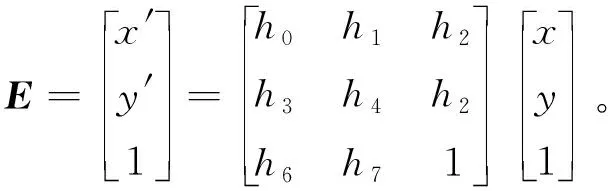
(5)
RANSAC算法的主要步骤如下:
① 在特征点初始匹配的数据集中随机选取4对非线性特征点作为样本数据,记为模型M,然后计算出单应性矩阵E,设定好阈值;
② 使用E计算出初始匹配数据集中所有数据与模型M的投影误差,若误差小于设定的阈值,则将该数据加入内点集Q;
③ 若当前内点集Q中的元素个数大于当前最优单应性矩阵的内点数,则对当前最优单应性矩阵进行更新,同时更新迭代次数。反之,不更新;
④ 根据当前最优单应性矩阵的内点数更新迭代总次数,若当前迭代次数小于总迭代次数,返回执行步骤①。反之,则当前模型M就是待求的模型。
3 实验与分析
为了验证本文提出的算法,选取城市、岛屿及河流3种场景下的无人机遥感图像进行实验,基准图像和待配准图像来源于互联网地图平台的卫星地图,如图3所示。
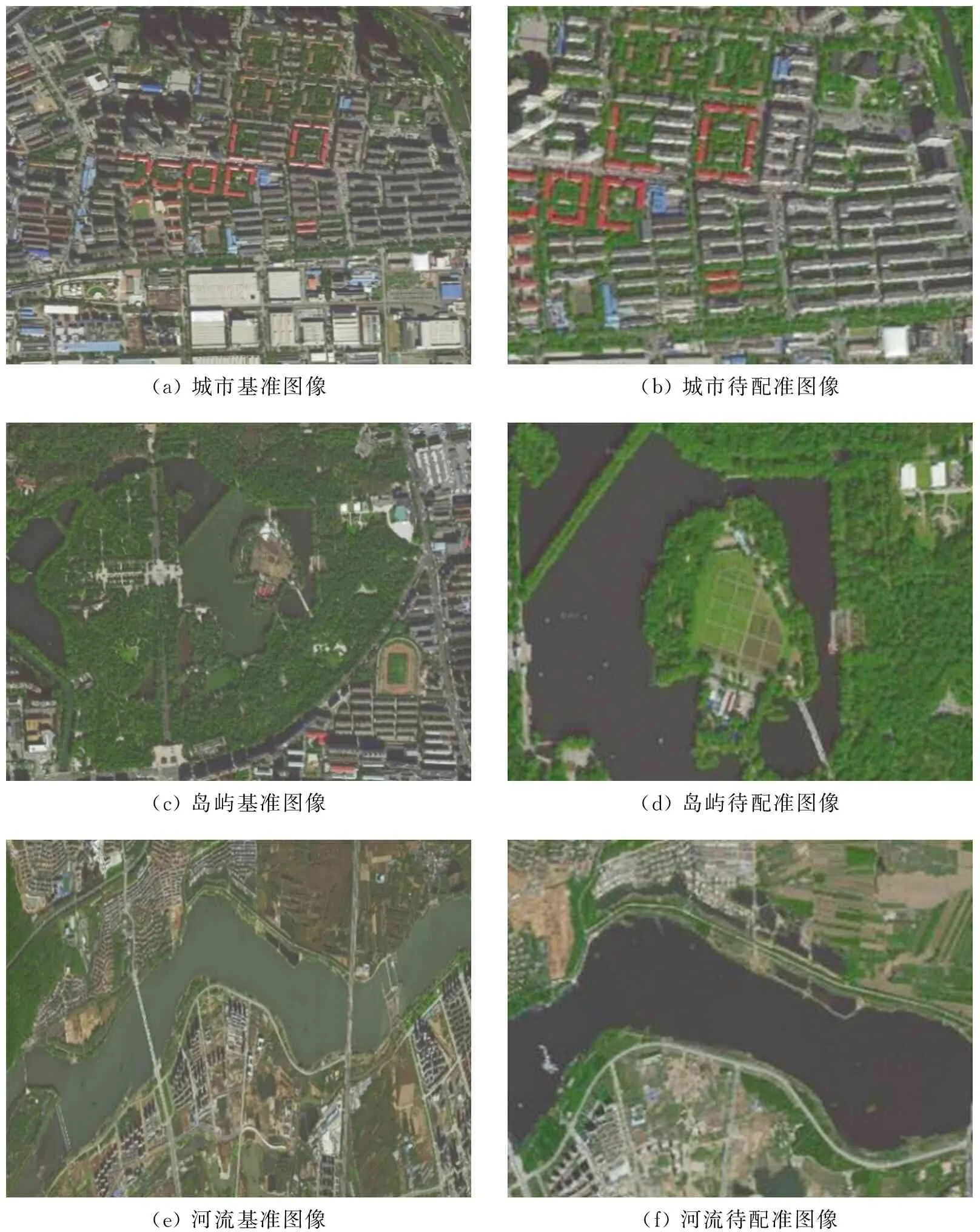
(a) 城市基准图像(b) 城市待配准图像(c) 岛屿基准图像(d) 岛屿待配准图像(e) 河流基准图像(f) 河流待配准图像
基于上述遥感图像,分别利用SIFT、SURF以及SURF-BRISK 3种算法进行图像配准,结果如图4~图9所示。将计算运行时间、匹配点对数以及匹配点对的均方根误差作为图像配准效果的评价指标, 结果如表1所示。
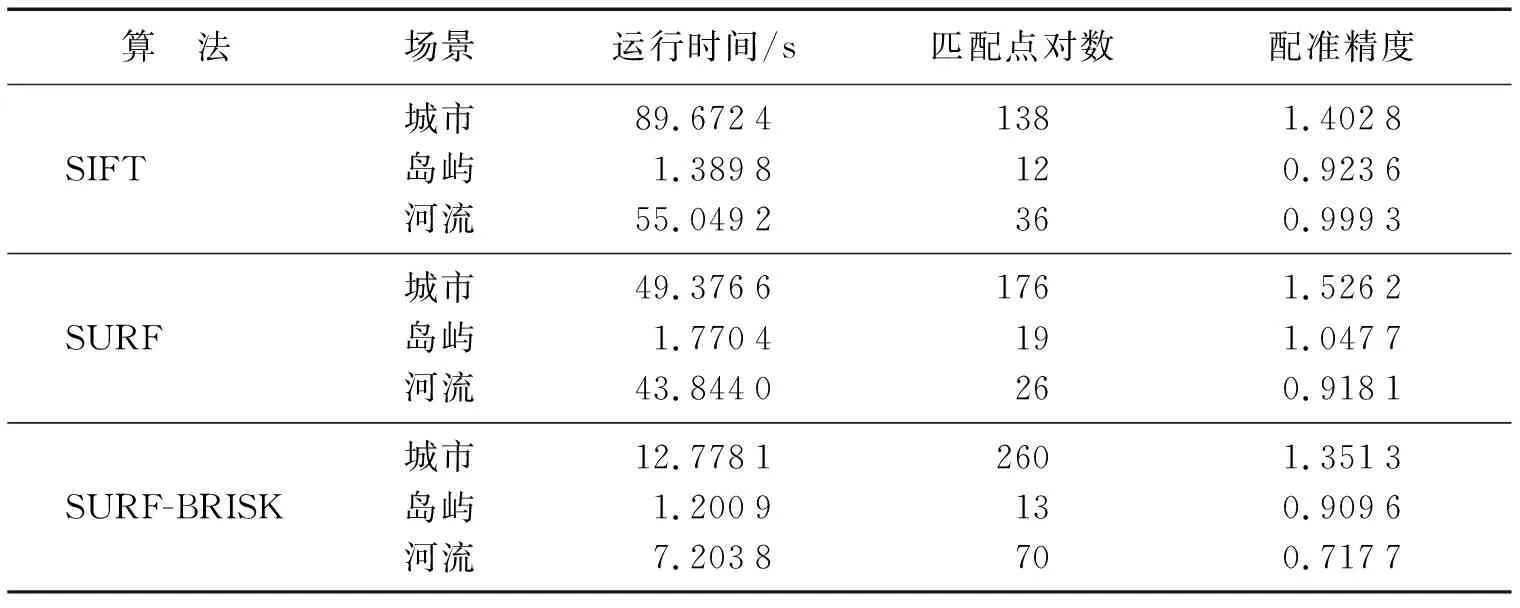
表1 SURF-BRISK算法与 SIFT算法和SURF算法的比较结果Table 1 Comparison results of surf-bridge algorithm with SIFT algorithm and SURF algorithm

(a) SIFT(b) SURF(c) SURF-BRISK

(a) SIFT(b) SURF(c) SURF-BRISK
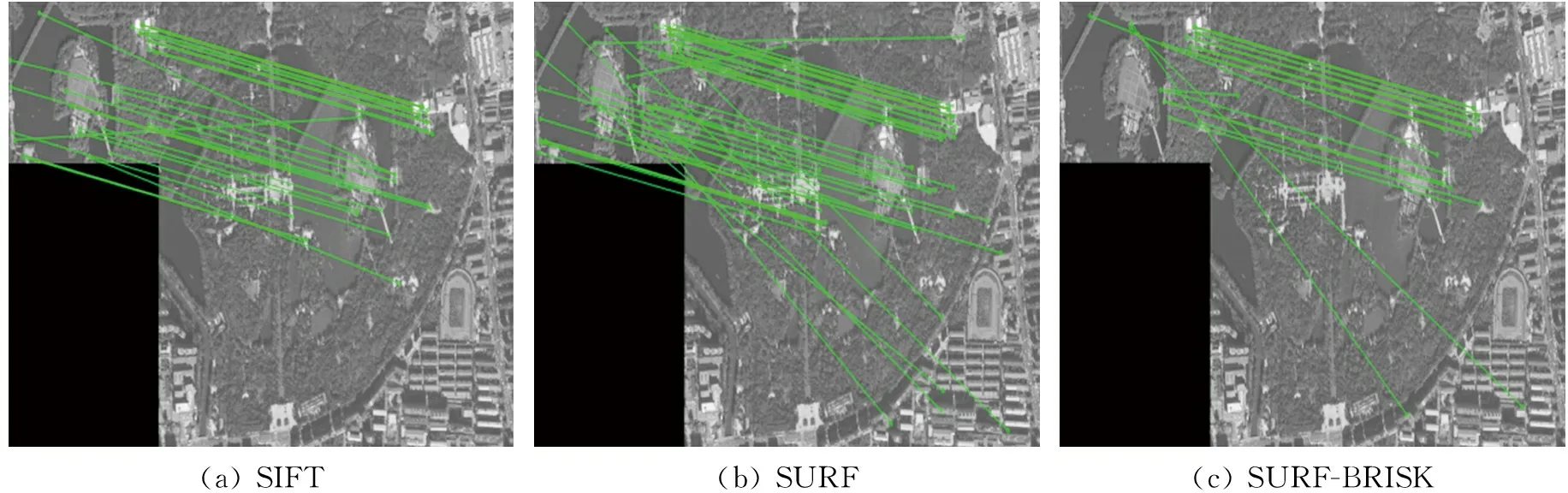
(a) SIFT(b) SURF(c) SURF-BRISK
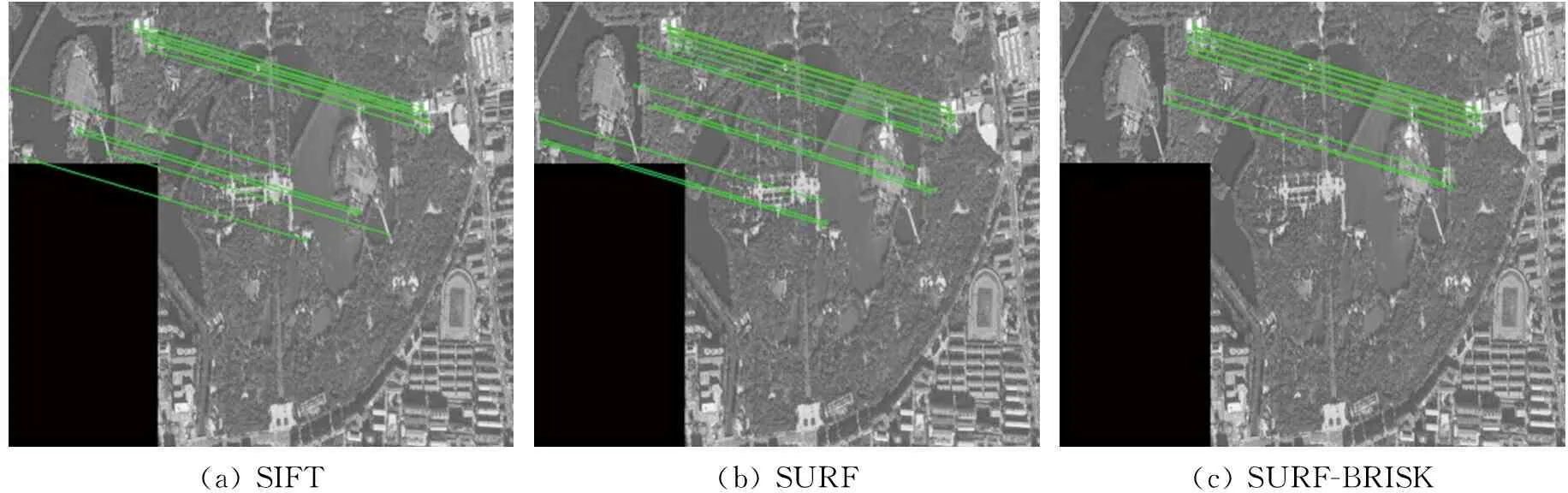
(a) SIFT(b) SURF(c) SURF-BRISK

(a) SIFT(b) SURF(c) SURF-BRISK

(a) SIFT(b) SURF(c) SURF-BRISK
通过图4~图9的配准结果以及表1中的对比数据可知:SURF-BRISK算法可以有效剔除粗匹配中的误匹配点,优化图像配准结果;和其他传统算法相比,SURF-BRISK算法对于不同场景下的无人机影像配准都能够取得较好的效果:以城市场景为例,SURF-BRISK算法的运行时间相对于SIFT算法、SURF算法分别减少了约86%、74%,而配准精度分别提高了约4%、13%,匹配点的对数也有大幅提升。
通过以上实验分析可知: SURF算法可以更快地提取出更多的图像特征点,BRISK算法可以更快地生成特征描述符,且二者均具有良好的旋转、缩放不变性及抗噪性,SURF-BRISK算法属于“强强联合”。对于无人机遥感影像配准,SURF-BRISK 算法能够取得较好的效果,相对于传统算法在运行时间上有较大的提升,配准精度虽提升不大,但对于无人机视觉导航的图像配准任务来说,细微的提高都将对定位精度产生积极的影响。
4 结 论
本文针对无人机遥感影像配准,对SURF算法进行改进, 提出了SURF-BRISK算法,将SURF特征点提取与BRISK特征点描述符相结合,在无人机影像配准中有效地提升了算法的运行速度;采用FLANN算法进行特征点粗匹配, 然后通过RANSAC算法进一步剔除误匹配点,有效地降低了误匹配率。经实验验证,SURF-BRISK算法在保证配准精度的同时可以很好的提高运行效率,满足无人机航拍图像匹配对实时性与精确度的要求。

