CFRP板加固H型钢梁抗弯承载力计算方法
周 乐, 祝梦繁, 赵同峰
(1. 沈阳大学 建筑工程学院, 辽宁 沈阳 110044;2. 辽宁省桥梁安全工程专业技术创新中心, 辽宁 沈阳 110122;3. 辽宁省交通高等专科学校 道路与桥梁工程系, 辽宁 沈阳 110122)
随着我国经济发展和科学技术水平的不断提高,建筑物呈现出高度更高、跨度更大的趋势。钢结构具有强度高、自重轻、延性好等优势,能更好地满足建筑结构的要求,是目前大面积厂房、展览馆、体育馆的主体结构[1]。由于设计、施工、材料选取不当等问题,使得现有钢结构存在各种各样的缺陷和损伤[2],而拆除重新安装则会消耗大量的财力和物力。因此钢结构的加固及改造成为研究的热点问题。
纤维增强复合(fiber reinforced polymer, FRP)材料,具有轻质高强、耐久性能好、抗疲劳性能好、可设计性强等优点,被广泛应用于结构加固领域。FRP材料根据纤维的不同可分为碳纤维增强复合材料(CFRP)、玻璃纤维增强复合材料(GFRP)等,其中CFRP材料的应用最为广泛。采用CFRP材料加固钢结构的方法主要有粘贴加固法、预应力加固法2类。
为研究CFRP材料加固后对结构力学性能的提高程度,Miller等[3]进行了CFRP板加固钢梁刚度的试验研究,结果表明,经过CFRP板加固的钢梁刚度提高10%以上;Colombi等[4]对CFRP板加固钢梁抗弯承载力进行了试验,结果表明,粘贴CFRP板可以有效提高钢梁的抗弯承载力;王勃等[5]对不同层数CFRP布加固受弯钢梁进行了有限元分析,结果表明CFRP布加固可以提高钢梁的屈服载荷、极限载荷及刚度;陈亚飞等[6]对2次受力下CFRP板加固的钢梁受弯承载力进行了有限元模拟,分析显示CFRP板可以有效提高钢梁的抗弯能力,但提高的效果受初始应力影响。
为研究CFRP材料加固后结构的承载力计算方法,周乐等[7]通过等效截面替代法将CFRP筋等效为钢筋,得到了计算梁的等效配筋率,进而得到混合配筋梁的抗弯承载力公式;曹靖[8]通过对加固钢梁界面应力的推导,得到界面剥离应力和剪切应力的通用公式,从而计算得到钢梁承受的各种外力对应值;周乐等[9]通过叠加法对FRP加固钢筋混凝土梁截面受力情况进行分析,求得外包FRP钢筋混凝土梁不同状态下的极限抗弯承载力计算公式。
1 CFRP板加固钢梁抗弯承载力计算
CFRP板加固受弯钢梁的常见方法是将CFRP板用结构胶粘贴在钢梁底部,使钢梁与CFRP板协同受力。由于钢梁与CFRP板材料属性不同,在计算加固梁抗弯承载力时不能使用纯钢梁抗弯承载力计算公式,本文参照文献[9]提及的叠加法,对CFRP板粘贴加固H型钢梁的弹性工作阶段抗弯承载力计算公式进行推导并验证。
1.1 基本假定
1) 假定胶层的剪应力沿胶层厚度方向均匀分布,CFRP板与钢梁黏结良好;
2) 不考虑胶层的弯曲变形及CFRP板与钢梁的剪切变形;
3) 假定加固钢梁在粘贴CFRP板前后皆满足平截面假定。
1.2 材料的本构关系
1.2.1 钢材的本构关系
将钢材视作理想的弹塑性材料,其本构关系可以分为屈服前和屈服后2个阶段:达到屈服点之前,钢材处于弹性阶段,钢材应力-应变关系为线性分布;达到屈服点之后,钢材进入塑性阶段,应力保持不变。应力-应变关系如图1所示,计算公式为:
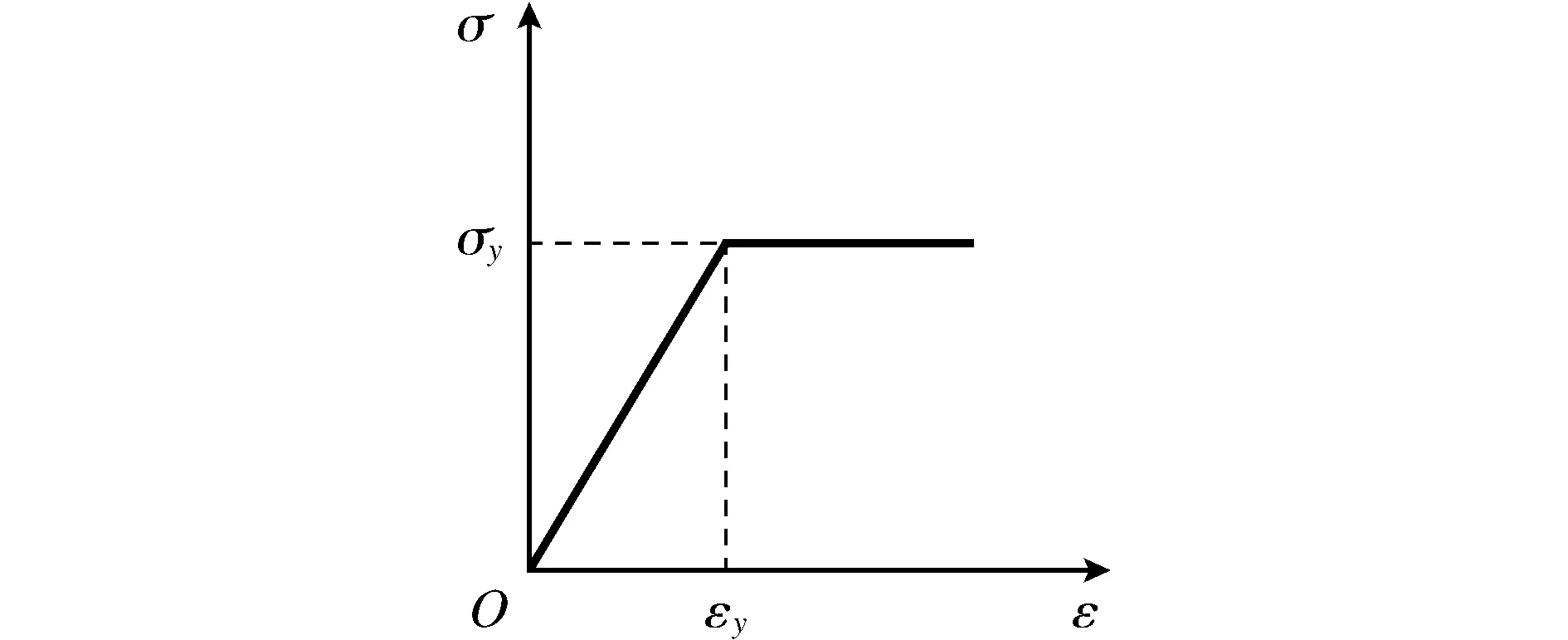
图1 钢材的应力应变关系Fig.1 Stress-strain relationship of steel
式中:σs为钢材应力;εs为钢材应变;Es为钢材弹性模量;εy为钢材屈服应变;fy为钢材屈服应力。
1.2.2 CFRP材料的本构关系
在CFRP材料破坏之前,其本构关系始终保持线性关系,CFRP材料的应力-应变关系如图2所示。计算公式为
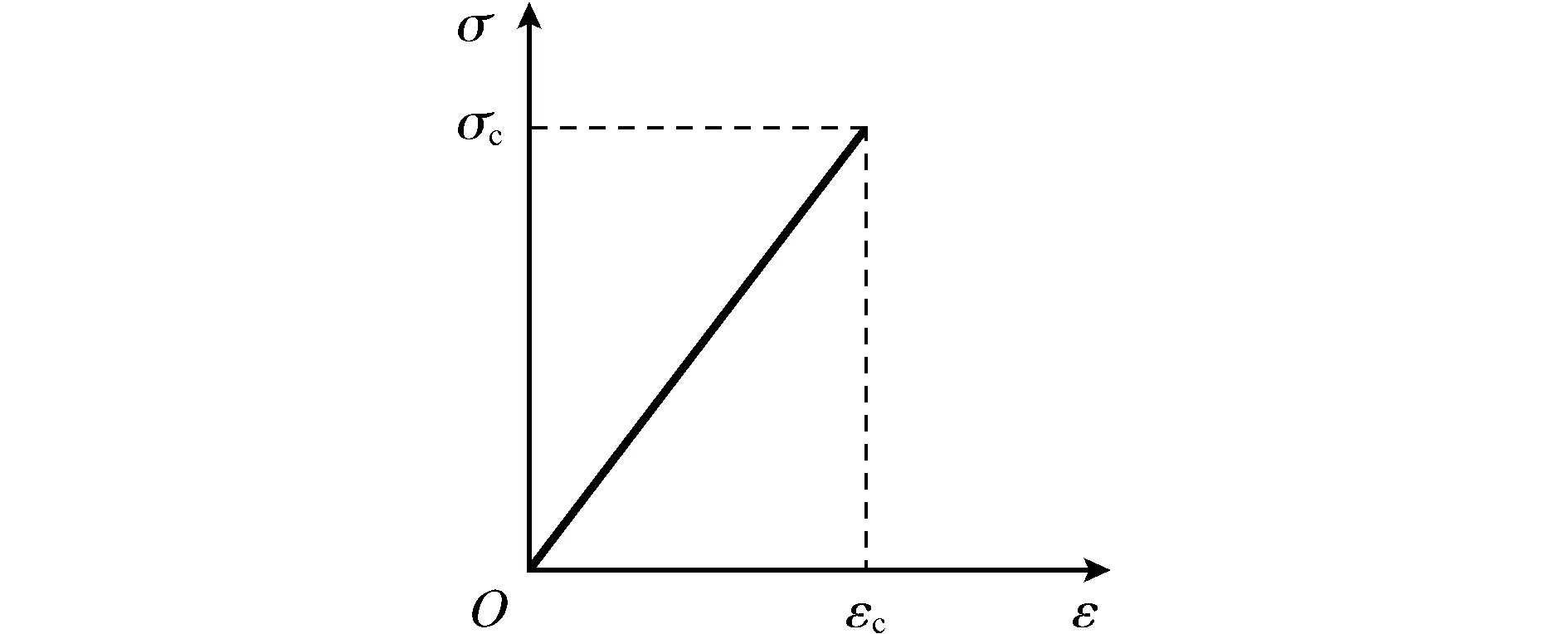
图2 CFRP材料的应力应变曲线Fig.2 Stress-strain curves of CFRP materials
σc=Ecεc。
式中:σc为CFRP材料应力;Ec为CFRP材料弹性模量;εc为CFRP材料的应变。
1.3 抗弯承载力计算公式
加固梁在弯矩作用下,按截面应力-应变分布可分为3个阶段:弹性工作阶段、弹塑性工作阶段及塑性阶段。其中在弹性工作阶段中,钢梁承受的弯矩较小,应力、应变呈三角形分布,如图3所示。弹塑性工作状态下,梁截面边缘应力达到屈服应力,此时边缘部分进入塑性状态,但边缘以内部分仍处于弹性工作状态,该部分称为弹性核,此时的应力、应变分布如图4所示。塑性阶段下,钢梁全截面进入塑性状态,此时变形会继续增加,但承受载荷不再增加,已经不能继续使用。
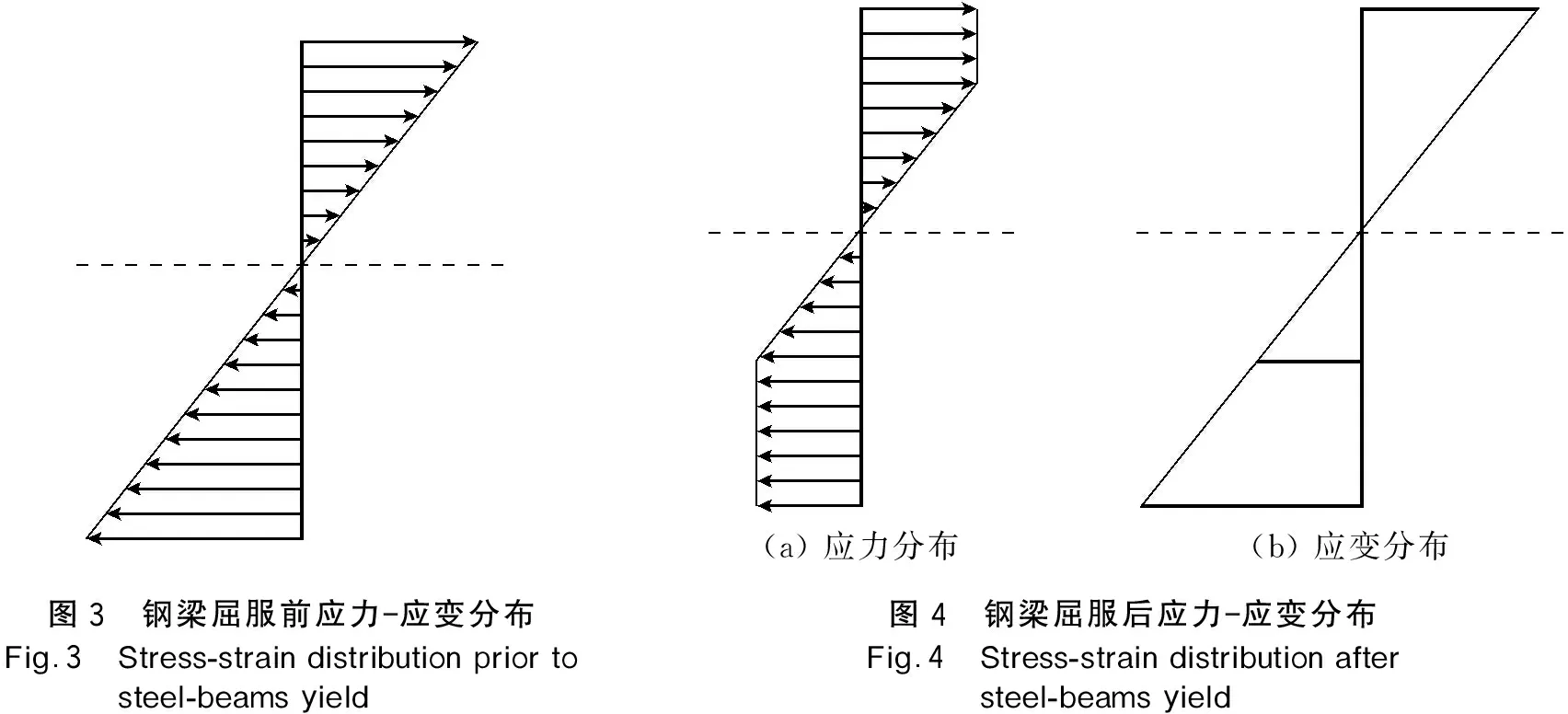
(a) 应力分布(b) 应变分布图3 钢梁屈服前应力应变分布Fig.3 Stress-strain distribution prior to steel-beams yield图4 钢梁屈服后应力应变分布Fig.4 Stress-strain distribution after steel-beams yield
底部粘贴CFRP材料加固的钢梁的破坏模式[10]有如下几种:
1) 钢梁腹板失稳破坏;
2) 钢梁受压翼缘出现局部屈曲;
3) 钢梁底部受拉翼缘屈服;
4) CFRP材料端部出现剥离破坏;
5) CFRP材料中部出现剥离破坏;
6) CFRP材料与胶层发生剥离;
7) 钢梁与胶层发生剥离。
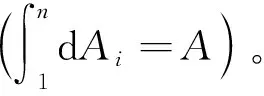
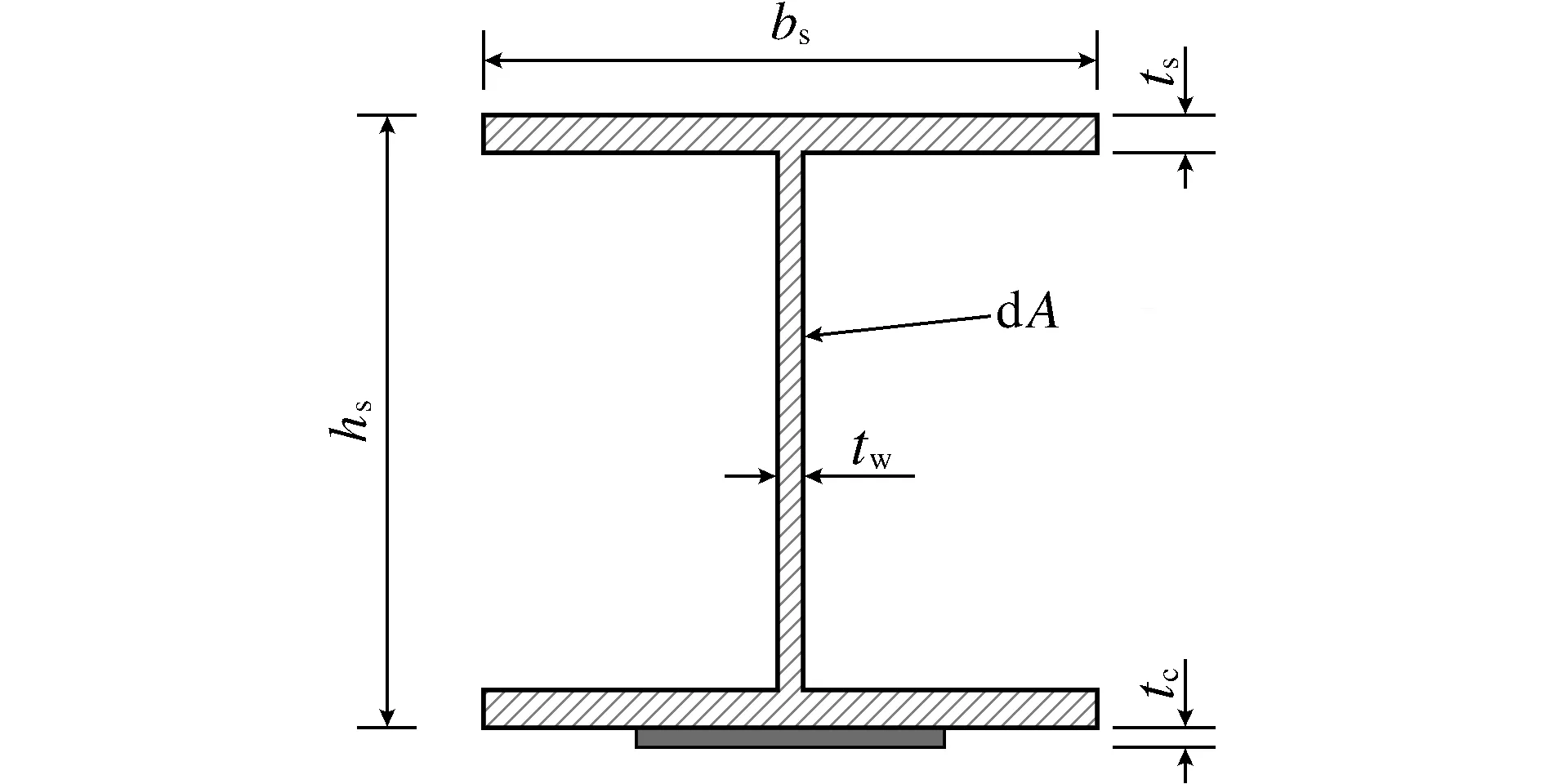
图5 加固梁截面Fig.5 Reinforced beam cross-section
根据平截面假定可得到加固梁截面曲率ρ,

(1)
根据曲率ρ可以求得受压区第i处的应变εs,i、受拉区第j处的应变εt,j、受压翼缘及受拉翼缘处的应变εs、εt和CFRP板的应变εc分别为:
式中:yi为受压区i处到中和轴距离;yj为受拉区j处到中和轴距离。

(5)
式中:σs,i为受压区i处的压应力;σt,j为受拉区j处的拉应力;dAi为受压区i处的面积微分;dAj为受拉区j处的面积微分;As为钢梁受压区面积;At为钢梁受拉区面积;Ac为CFRP板截面面积。
对截面中心取矩,可得截面弯矩等于外加弯矩,即

(6)
在明确上述基本公式后,对加固梁的屈服弯矩计算公式进行推导。加固梁弹性工作状态下截面受力及应变分布如图6所示,图中:h为加固梁截面高度(包含CFRP板厚度);Cf为受压翼缘板所受压力;Cw为腹板受压部分所受压力;Tf为受拉翼缘板所受拉力;Tw为腹板受拉部分所受拉力;Tc为CFRP板所受拉力;My为钢梁屈服弯矩;εs为钢梁受压翼缘处应变;εt为钢梁受拉翼缘处应变;εc为CFRP板应变。
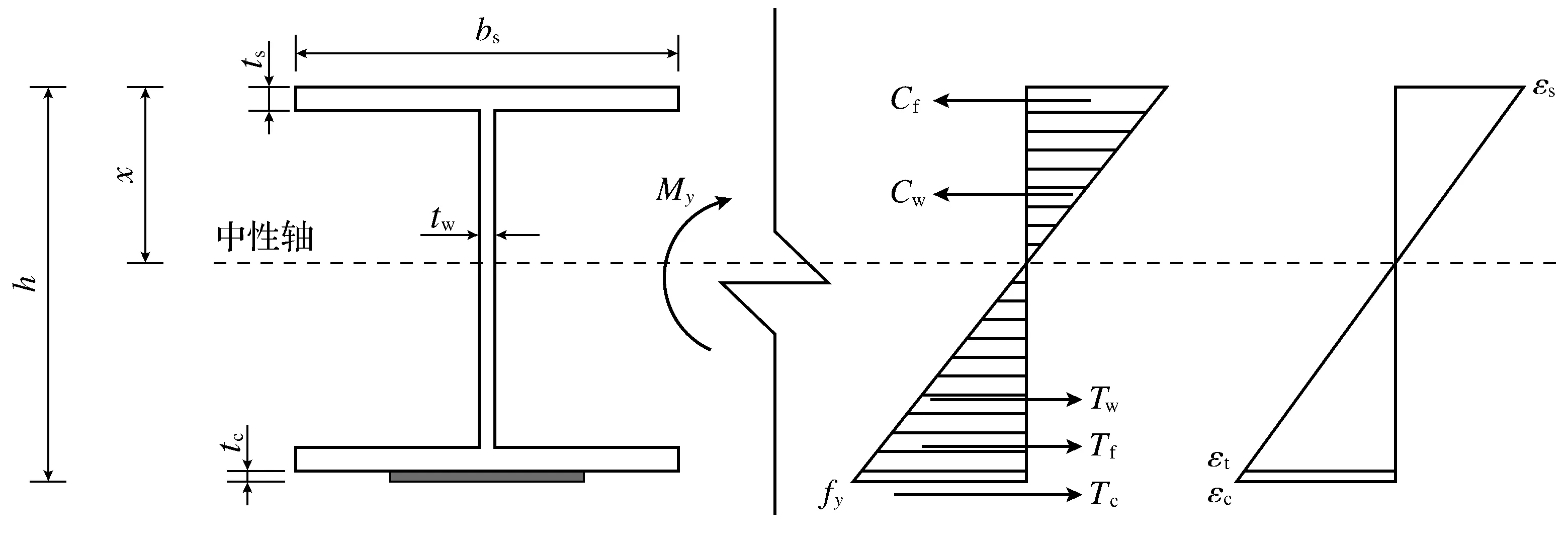
图6 加固梁截面及应力应变分布示意Fig.6 Schematic diagram of reinforced beam section and stress-strain distribution
加固梁截面以中性轴为界划分为受压区和受拉区,令受压区上侧到中性轴的距离为x。以钢梁受拉区边缘应力达到屈服应力fy为标志进行计算,此时的受拉翼缘板所受拉力为
Tf=fytsbs。
(7)
针对腹板受拉区所受的拉力,取腹板受拉区段中点处应力值作为受拉区段的平均应力进行计算,此时腹板受拉区所受拉力为
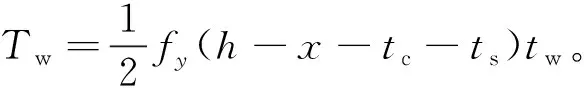
(8)

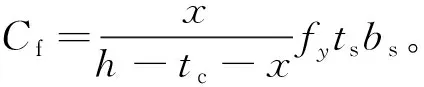
(9)
针对腹板受压区所受压力的计算与受拉区同理,取腹板受压区中点处应力值计算,此时腹板受压区所受压力为
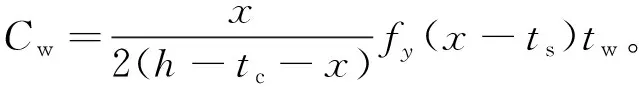
(10)
因为CFRP材料属于线弹性材料,故CFRP板的拉力可由CFRP板的应力值乘以截面面积求得,CFRP板所受拉力为
Tc=EcεcAc。
(11)
由平截面假定可求得CFRP板应变

(12)
由式(5)可得Cf+Cw=Tw+Tf+Tc,将式(7)~式(11)代入得到式(13),
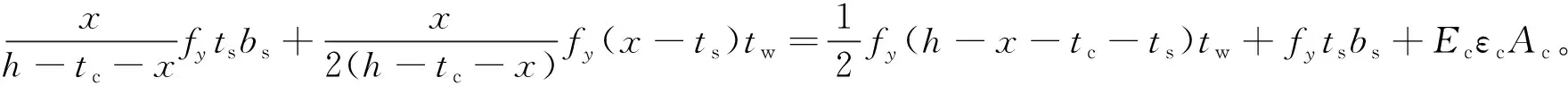
(13)
由式(12)、(13)联立可以求得x,之后对中性轴处取矩,可以得到加固梁弹性工作状态下的屈服弯矩My,
式(14)即为弹性工作状态下CFRP板加固H型钢梁抗弯承载力计算公式。
2 抗弯承载力计算公式验证
为验证本文推导的加固梁抗弯承载力公式的正确性,参照文献[11]中2根试验梁的相关试验数据进行公式验证。
试验选用的2根钢梁为Q235的H型钢梁,其中1根底部粘贴CFRP板加固,编号为L1;另1根不作处理,编号为L0。加固梁L1截面形式及H型钢梁和CFRP板的截面尺寸如图7所示。钢梁屈服强度fy为235 MPa,弹性模量Es为205 GPa;CFRP板的弹性模量Ec为173 GPa。

图7 加固梁截面(单位: mm)Fig.7 Section of the reinforced beam (unit: mm)
将试件L0和L1的截面参数(h、ts、bs、tw、tc等)以及性能参数(Es、fy、Ec等)代入式(12)、(13)中可求得受压区边缘距中性轴的距离x,之后将x代入式(7)~(11)中分别求得加固梁截面受压区和受拉区各部分所受的压力和拉力,最后根据式(14)得到钢梁的屈服弯矩的计算值,其试验结果与计算结果对比情况如表1所示。

表1 钢梁屈服弯矩My数据对比Table 1 Data comparison of steel beam yield bending moment My
由表1可知,计算值与试验值的比值接近1,说明本文推导的计算公式可以计算出CFRP板加固H型钢梁弹性工作阶段的抗弯承载力。
3 结 论
1) CFRP板与H型钢梁可以协同工作,并且加固梁的抗弯承载力可以通过推导公式计算得到。
2) 加固梁工作过程中,梁底受拉翼缘达到屈服强度是由弹性工作阶段过渡至弹塑性工作阶段的标志,此时对应的外部弯矩为加固梁的屈服弯矩。
3) 通过叠加法推导得到了加固梁达到屈服强度时的屈服弯矩理论计算公式,使用该计算公式得到的计算值与试验结果吻合良好,误差在可以接受的范围内,该计算公式可以对非预应力CFRP板加固钢梁抗弯承载力计算提供一定的参考。

