智能装填系统中的自适应轨迹规划设计

袁立达，关晓存，管少华，吴宝奇

(海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉 430033)

某智能装填系统是电磁线圈装置中主要分系统之一,可完成多块电枢的快速装填。在每次电磁线圈放电发射后,线圈装置受到反作用力而发生冲击振动。反作用力通过液压及弹簧机构进行缓冲,线圈位置可在620 ms内趋于稳定。

每次发射后,在不同能级下及不同电枢下电磁线圈位置发生偏移量不同,虽然能在短时间内稳定,但是稳定的位置不同,如果不能根据实际位置修正装填的终点位置就难以保证每次装填精确到位,因此要求智能装填系统能够自适应改变装填的终点位。笔者运用激光位移传感器对系统进行了冗余设计,使得每次发射后不论线圈的位置如何变化,装填终点位均能在500 μs内适配线圈位置,从而保证在发射时,电枢与线圈的相对位置误差在0.3 mm以内,确保正常发射。

1 自适应轨迹规划

1.1 国内外对该技术的研究成果

Kim等采用了非线性轨迹修改和使用新的启发式函数来研究保持能量效率的控制算法,与使用梯形速度剖面的常规轨道相比,生成的运输轨道可以节省能源[1]。Chen等提出了一种新的自适应伪谱(NAP)方法来求解时间-能量最优控制模型,以最小化停车时间和车辆的能量输出。结果表明,NAP法在求解时能最优控制模型问题时具有更高的计算效率和精度[2]。Song等设计了一种基于RBF神经网络的自适应鲁棒控制器来处理非线性和不确定性问题,仿真结果表明,该方法保证了机器人在轨迹规划过程中的平稳运行[3]。Zhou等提出了一种基于邻域最优控制理论的高超声速拦截中段弹道在线优化修正算法,该算法以当前状态偏差和修正后的终端约束为输入,生成最优控制修正。该方法与粒子群算法和广义预测方法相比,具有与广义预测方法等价精度高、计算效率高等优点[4]。

黎宇晨等提出了结合碰撞检测的三维A*算法,相比较于传统的A*算法,在保留局部最优的同时计算周围的最优,进而达到路径的最优,考虑了全局,更加的具有效率性以及精准性[5]。赵波等利用机械系统动力学分析软件ADAMS中的运动学分析模块,模拟挖掘机在特定挖掘轨迹下3个驱动杆件的运动关系,以解决平面多自由度运动学逆问题的求解难题,利用此种直观的运动轨迹求逆的方法规划了液压控制系统多执行器协同工作的输入参数,实现挖掘机的自动平整操作控制[6]。唐峰润等提出一种基于轨道状态评估的自适应在线轨迹规划方法,所提方法能使锌电解行车有效载荷的摆角小于1°,在总长60 m的轨道条件下,行车的定位误差小于3 mm;与人工驾驶相比,减速制动阶段的制动效率平均提高28%,取得了良好的运行效果[7]。管萍等将自适应模糊控制应用于高超音速飞行器,并给出了模糊控制系统的详细设计过程。根据跟踪误差,在线调整模糊系统的标尺参数,使系统能够近似高超音速飞行器的不确定非线性函数。通过李雅普诺夫理论,推导了自适应定律,并证明了整个系统是均匀的最终有界的。仿真结果表明,所提出的控制律能有效抑制扰动,具有较好的动态和静态性能[8]。

国内外对于自适应轨迹规划控制主要采取各种优化的控制策略及算法,侧重于整个运行轨迹的修正和优化,从而提高效率达到减少能量损耗的目的;并且均具有仿真模型以及相对应的实验验证。

1.2 研究内容及创新点

笔者研究的主要内容是对智能装填系统中的装填终点位进行精确实时的在线自适应控制。创新点在于将PLC轨迹规划技术、激光测距技术及实时工业以太网相结合并运用在智能装填中。研究中运用PLC标准运动控制功能块Mc_MoveAbsolute,并通过激光实时采样位置数据,对数据进行转换处理,再实时对终点位的设定进行修改。本研究使得电机的位置控制具备一定的自适应性,不需要人为参与调节,每次发射后及时响应,瞬时调节,从而起到自适应控制终点位的作用。

智能装填系统中电机的轨迹规划通过PLC给定。笔者采用了双S型轨迹规划技术,对电机速度控制进行平滑处理,使得电机不会承受瞬时变化较大的作用力,从而延长电机及机械使用寿命。电机在加速段中速度随时间变化曲线如图1所示,蓝色曲线为PLC给定的速度曲线,红色曲线为电机实际运行速度曲线。

设匀速段的速度为v,加速度为a,加加速度为J。双S型7段轨迹规划中前3段的时间组成加速段时间,分别为T1,T2,T3,T为电机加速段时间[9-10]。基于双S型7段轨迹规划,初速度为0的情况下,各时间段公式如下:

(1)

(2)

T=T1+T2+T3.

(3)

可推导出加速段时间T的公式:

(4)

电机速度为2 m/s,加速度为10 m/s2,加加速度为80 m/s3,根据公式计算可得加速段时间为0.325 s,与实验数据相符。

在电机行程末端终点位的控制上采用了一种基于激光测距技术的自适应控制,研究中自适应轨迹规划主要是一种在线的实时修正。其具体的实现是采用激光测量身管的实时相对位置,并在电机启动前改写目标位置及其运行过程中修正目标位置,从而确保每次装填到位时,在装填终点位均能将电枢装填至对应的位置。

2 激光位置检测

2.1 激光测距技术及其原理

激光测距的常用方法有相位法、脉冲法、干涉法及三角法[11-12]。激光测距的基本原理是测量激光在目标位置与光源往返一次的时间从而推算出距离。假设光速在空气中恒定不变,可以得出距离的计算公式:

(5)

式中:S为激光光源与所测目标之间的距离;c为光在空气中传播速度;t为激光光束在光源与目标之间的往返时间。

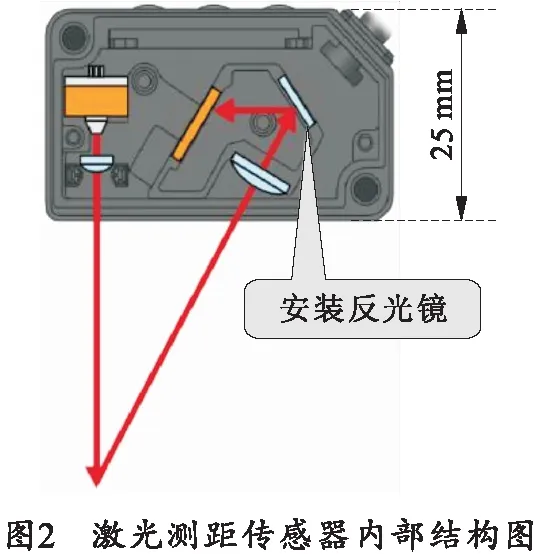
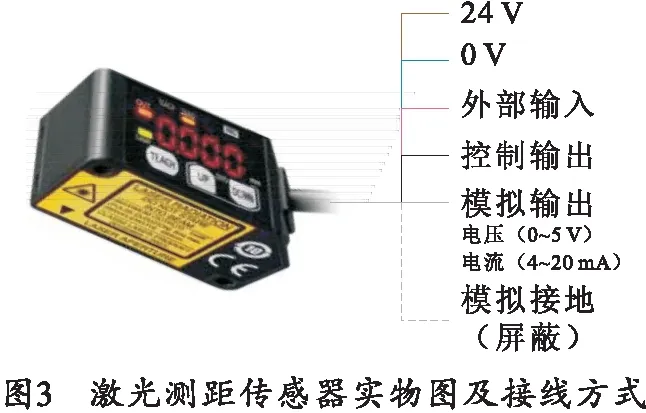
本研究采用松下HGC-1400激光位置传感器,该传感器精度范围在0.3 mm内,测量范围为400 mm(±200 mm),并可将模拟量信号读入PLC中。在200 mm和600 mm处分别对应的脉冲数为32 767和0,对应的模拟量为20 mA和4 mA。经过计算得出单个脉冲对应12.207 031 25 μm。该激光位置传感器设计了一种新型的内部安装有镜面的光学系统,如图2所示。该传感器运用的是三角法测距技术,其基本原理是基于几何三角形,激光光源、测量目标和反射接收系统构成三角形结构。在参考平面下,光源反射到CMOS光学元件上,可得到一点。在测量目标平面下,光源反射到CMOS上可得到另一点。根据角度及比例计算两点之间的距离,可以得出测量目标的位置[13-14]。激光测距传感器实物图及接线方式如图3所示。

2.2 激光位移测距传感器布局设计

在发射过程中,电磁线圈装置会受到强大的冲击振动,而线圈通过液压弹簧机构进行缓冲。由于身管固定在基座上,相对位置并不会发生变化,且无冲击振动影响。因此设计将激光测距传感器安装在身管的下方,反光板则安装在通过液压弹簧与电磁线圈连接的背板上。具体如图4所示。

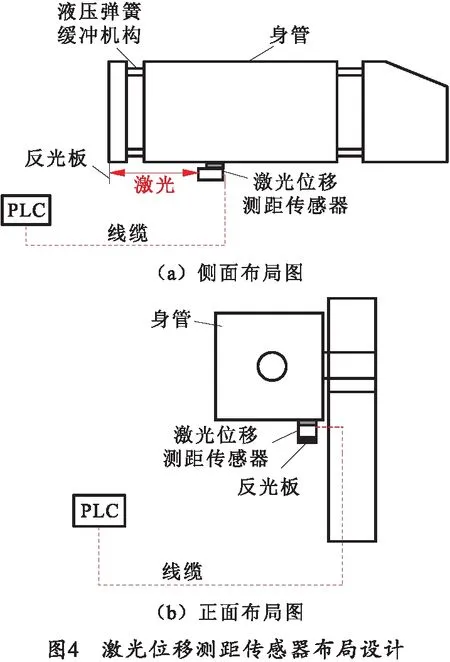
激光测距位移传感器通过M3型螺钉及安装架安装在身管底部,通过20 m长的RVVP4X0.75四芯双屏蔽线缆连接到远端的PLC主控制器。激光测距位移传感器安装位置与反光板之间控制在400 mm左右,因为该型传感器测距范围是200～600 mm之间,超出范围后将会出现测距数据无效的现象,400 mm处是根据实际位置变化而选择的位置。

3 总体设计

3.1 电气设计

研究采用24 V开关电源、倍福CX2020嵌入式PLC、EL9100电源模块和EL3054模拟量输入模块以及松下HGC-1400激光位移传感器搭建了测距系统实验平台,并进行了实验验证。测量的数据准确且各模块工作正常。平台如图5所示,激光数据曲线如图6所示。

由图6可以看出,激光数据精度范围在0.3 mm以内,由此可见整体系统精度可达±0.15 mm,满足研究需求。

3.2 软件设计

软件方面使用基于倍福CX2020的嵌入式PLC的TwinCAT3编程平台。该平台是基于现如今比较流行的EtherCAT实时工业以太网技术而开发的。EtherCAT技术是目前速率最快的以太网技术之一,上行下行的速率可达到100 Mbit/s,有着纳秒级别的同步精度,可以满足高精度的控制系统需求。

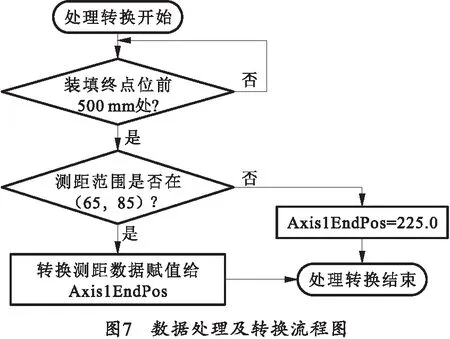
通过EL3054模拟量输入模块将激光测距传感器的模拟量输出采集到PLC中,从而得到一个脉冲数,不同脉冲数对应不同距离,经比例计算后赋值给RangingValue,计算得出对应RangingValue的装填终点位,名为Axis1EndPos。具体的数据处理及转换如图7所示,程序中还进行了保护设计,如果激光数据超出正常范围将设定终止位为最小值(装填最大行程位置),确保装填到位。

控制算法是采用基于PID控制的三闭环控制,控制中实时采集激光测距数据并择时进行终点位命令修正,其反馈控制流程图如图8所示。

研究中使用Mc_MoveAbsolute功能块(FB)对直线电机进行运动轨迹规划,将Axis1EndPos在相应时间进行Mc_MoveAbsolute功能块的目标位置的改写,可把算法封装成FB_CalcEndPos的动作(ACTION)。

由于采用EtherCAT网络通讯技术,装填装置的控制系统实时性较强,因此,经过前面的数据处理及转换后再通过控制功能块进行数据实时改写,进而改变装填终点位的设定,再根据运动控制功能块对电机运动轨迹进行规划,从而实现了装填系统的自适应轨迹规划。

在运行中及末端会进行参数的多次改写以保证装填的可靠性,需在前一个命令没结束时给定一个新的运动命令,由此需对Mc_MoveAbsolute功能块的BufferMode进行设定。BufferMode分为两类:一类为默认的Buffered(缓冲模式);另一类为Aborting(非缓冲模式)。缓冲模式下,新的运动命令只能在前一个命令完成后才可执行,而在非缓冲模式下,后续命令会导致正在运行的命令终止[10]。功能块参数配置如图9所示。

4 实验数据分析

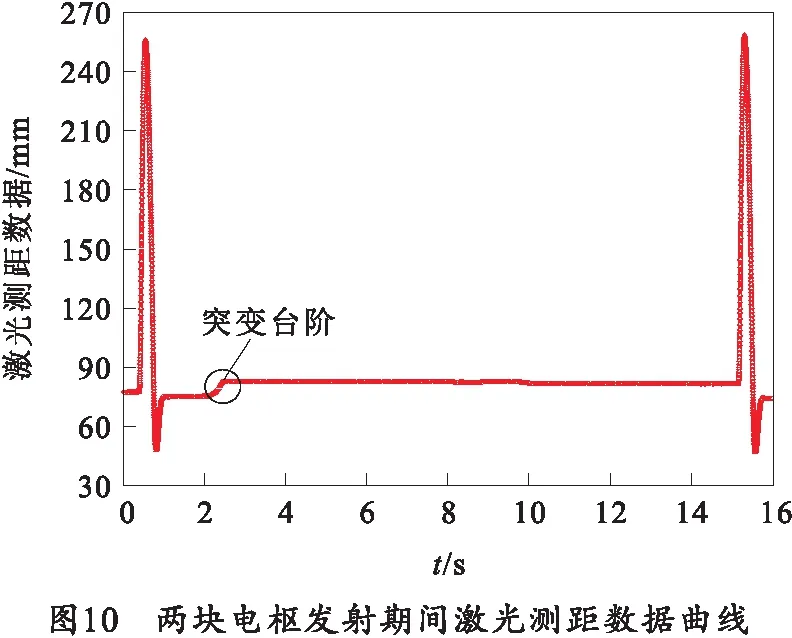
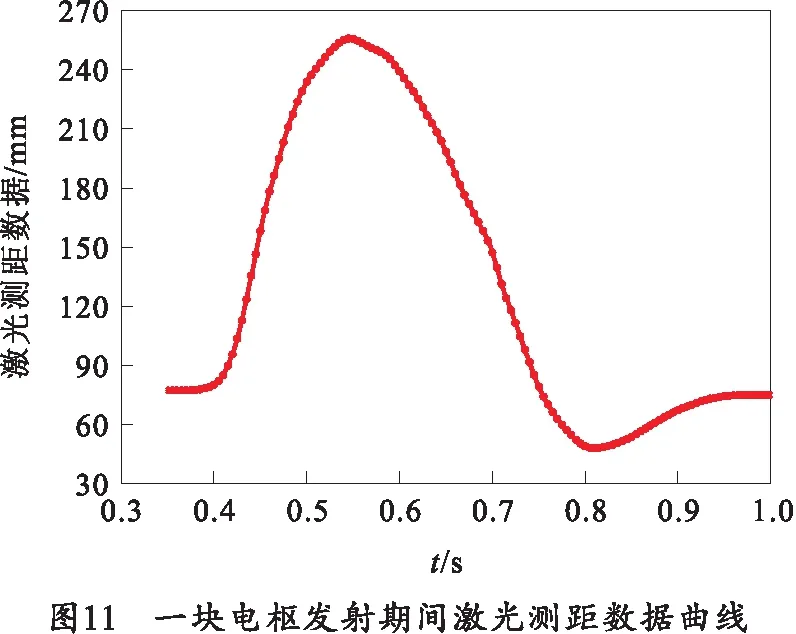
验证激光测距传感器的可行性,研究进行了两次自动装填,激光测距曲线如图10及11所示。可以看出在发射期间,电磁线圈在短时间位移变化幅度很大,并且发射后620 ms内由于液压和弹簧的共同作用,电磁线圈位置趋于稳定。然而第2次自动装填时,随动设备俯仰至装填角度,由于身管重力作用,线圈的位置会发生变化,在620 ms后,电磁线圈位置又一次趋于稳定。如图10中第1块电枢发射后激光曲线的一个突变所示。

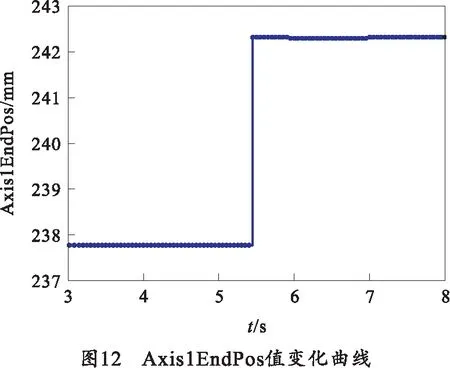
终点位设定值Axis1EndPos变化曲线如图12所示。结合图10以及图12,在第1块电枢装填并发射完成后,在某时刻进行了装填终点位的修正,使得第2次发射能够顺利完成。

智能装填装置直线电机位置曲线如图13所示。经分析,其终点位反馈与终点位跟随良好。经计算,位置控制超调在0.006%以内,位置偏差在12.2 μm左右。从图13(b)中可以看出两次轨迹规划的曲线是不同的,第1次终点位设定为237.788 2 mm,第2次终点位设定为242.322 1 mm,该数据的变化与图12中的Axis1EndPos数据变化相对应。

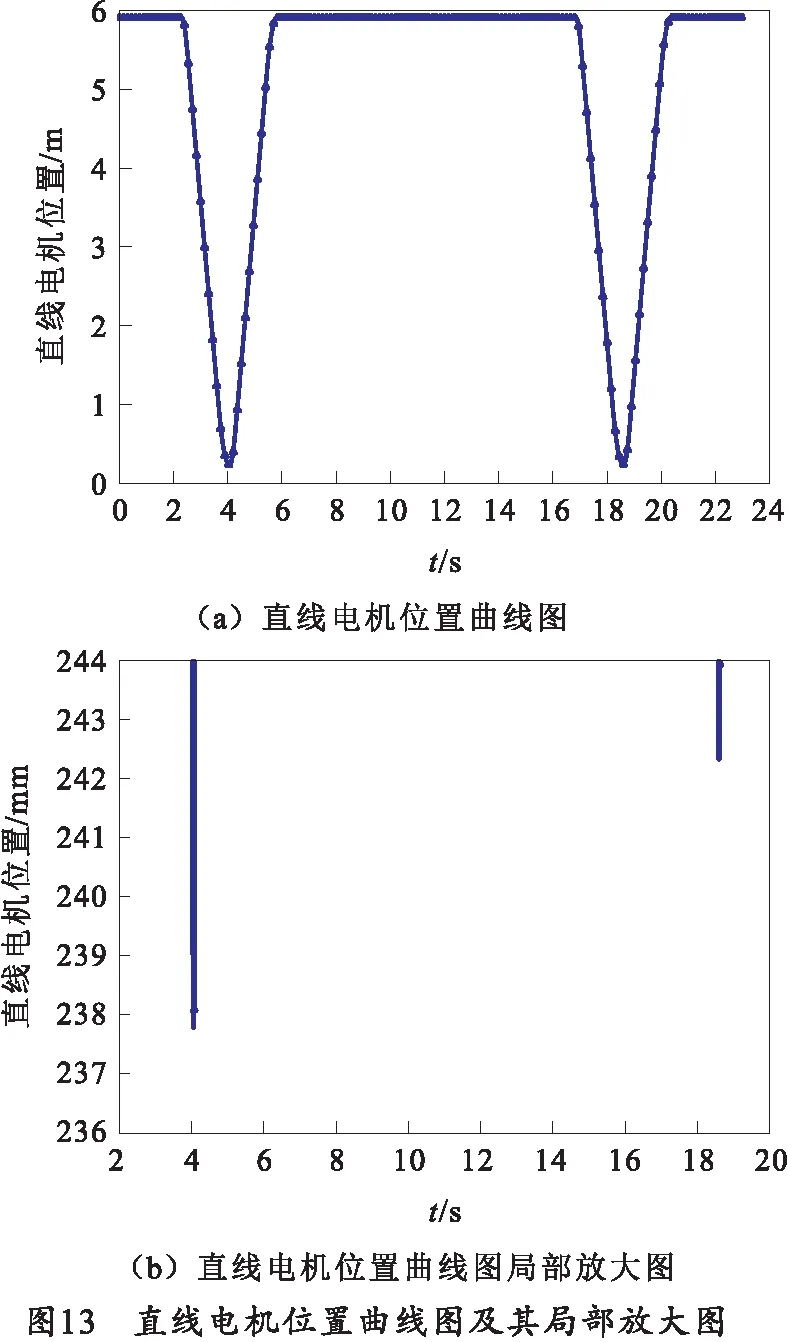
由此验证了在两次装填过程中对智能装填系统的装填终点位进行了自适应控制,实现了自动装填装置中直线电机的轨迹规划实时调节控制。

5 结束语

通过激光测距传感器的应用,电磁线圈装置中智能装填系统实现了装填终点位的自适应修正,确保了自动装填的鲁棒性、稳定性及冗余性,并且有着结构设计简单可靠,软件实现简单可行等优点。该设计满足简单可靠、功能复用的设计理念,解决了工程实践中的实际问题。后续将对身管的位置变化规律及理论进行深入研究,并选择合适可靠时机对装填的终点位进行修正。