沉垫基础在水平和斜坡黏土海床上的竖向承载特性研究
严远忠, 张 琪, 叶冠林, 孙 波, 刘国军
(1.上海交通大学 土木工程系, 上海 200240; 2.上海振华重工(集团)股份有限公司, 上海 200125)
我国大面积沿海区域的海床表面覆盖着一层深厚软黏土[1],传统自升式平台桩靴基础依靠桩腿提供竖向承载力,在软黏土海床中需要插桩很深才能满足承载力需求.面临插拔桩困难和桩靴刺穿等问题[2],自升式平台沉垫基础通过大面积基础坐底在海床表面,能有效减小对海床浅部土体的承载力要求,同时可避免插拔桩的难题[3-4],便于快速移动和作业.
目前针对在软黏土海床上沉垫基础的承载力研究主要以现场试验方法为主,结合有限元或浅基础承载力理论计算公式进行验证.Cox等[5]对位于大西洋海岸的Bethlehem沉垫基础进行现场试验,分析沉垫基础在风暴等环境荷载作用后发生附加沉降的规律,提出一种考虑土体弹塑性性质的沉垫基础极限承载力计算方法;Young等[6]监测位于密西西比河三角洲附近的沉垫基础在经历飓风后基础“刺入”土体的情况,发现沉垫基础入泥深度接近其厚度,承载力大于经典浅基础承载力公式所得计算值;喻旭明等[7]依托“三航工5”半潜式沉垫基础现场试验数据,采用美国石油学会(American Petroleum Institute,API)和挪威船级社(Det Norske Veritas,DNV)规范中的分析方法研究了软黏土海床上沉垫入泥时的稳定性与承载特性,建议采取土体的不排水抗剪强度指标计算沉垫基础的承载力.经典浅基础极限承载力计算公式由3项组成,其中Skempton公式和Vesic公式是常见的用于计算软土地基的极限承载力计算公式.Skempton公式[8]参数少、计算简便,但无法考虑地基倾角、倾斜荷载等情况;Vesic公式[9]通过不同承载力系数可将地基倾角、荷载倾斜等情况考虑在内,但计算公式较为复杂,两者各有优劣.
岩土贯入问题是一类高度非线性问题,采用传统拉格朗日方法会导致土体网格畸变进而造成计算不收敛,而在欧拉-拉格朗日法(Coupled Eulerian-Lagrangian, CEL)中欧拉体网格节点被固定,欧拉材料能在网格内部流动,避免了土体网格畸变,可有效解决岩土大变形问题.Qiu等[10]运用CEL方法分析了条形基础的竖向承载力,进一步将该方法应用于更加复杂的岩土边界值问题,结合解析解说明了CEL方法的有效性;Li等[11]研究了沉垫基础在自重作用下贯入土体的深度及由孔隙压力消散和蠕变产生的沉降规律,运用CEL大变形有限元方法进行数值模拟,结果表明有限元计算结果与实际工程情况吻合较好,可准确模拟结构物的贯入过程;王泽明[12]结合模型试验及CEL方法分析不同开孔率的裙式沉垫基础承载特性,验证了利用CEL方法分析海洋浅基础的可行性;徐蒙[13]利用CEL方法分析了不同结构形式防沉板贯入土体的阻力规律,发现防沉板的贯入阻力与海床土体体积隆起大小呈正相关.目前CEL大变形数值分析方法已被不少学者用于模拟岩土工程中的土体大变形计算问题并取得了较好结果.
综上所述,现有研究多采用现场试验方法确定沉垫基础的竖向承载力,耗时费力且不便于操作,对沉垫基础在水平和斜坡软黏土海床上的竖向承载特性也缺少相关研究.因此,本文结合离心机模型试验和数值方法,研究沉垫基础在水平和斜坡海床上的竖向承载特性与海床破坏模式的差异,通过T-bar试验确定海床土体不排水抗剪强度沿深度的变化规律,分析沉垫基础入泥过程中竖向承载力与基础底部孔隙水压力的变化规律,对比验证了离心机模型试验、数值计算和经验公式竖向承载力结果间的差异,对沉垫基础设计提供了参考.
1 离心机模型试验
自升式平台沉垫基础形状通常为正方形和长方形等,底面积巨大,如图1所示.采用常规1g模型试验(g为重力加速度)无法还原海床土体的实际应力状态,而离心机模型试验能有效解决该问题.

图1 沉垫型自升式平台Fig.1 Mat-supported jack-up platform
1.1 试验设备
离心机试验设备采用上海交通大学DC2200鼓式离心机,如图2所示.鼓槽直径R=2.2 m,径向深度L=0.4 m,高度H=0.7 m,总容重达600 g·t,最大离心加速度为200g.

图2 上海交通大学DC2200鼓式离心机Fig.2 DC2200 drum centrifuge of Shanghai Jiao Tong University
1.2 沉垫基础模型
基础模型采用铝合金材料,制作正方形和长方形两种基础形式,长×宽×高(L×B×H)分别为4 cm×4 cm×1 cm和8 cm×4 cm×1 cm.在沉垫基础底部安装孔压传感器测量基础底部超孔压,顶部连接轴力传感器测量其竖向承载力.试验模型箱内尺寸为62 cm×20 cm×35 cm,为避免模型箱边界影响,沉垫基础距离边界不小于8 cm[14],试验模型布置如图3所示.
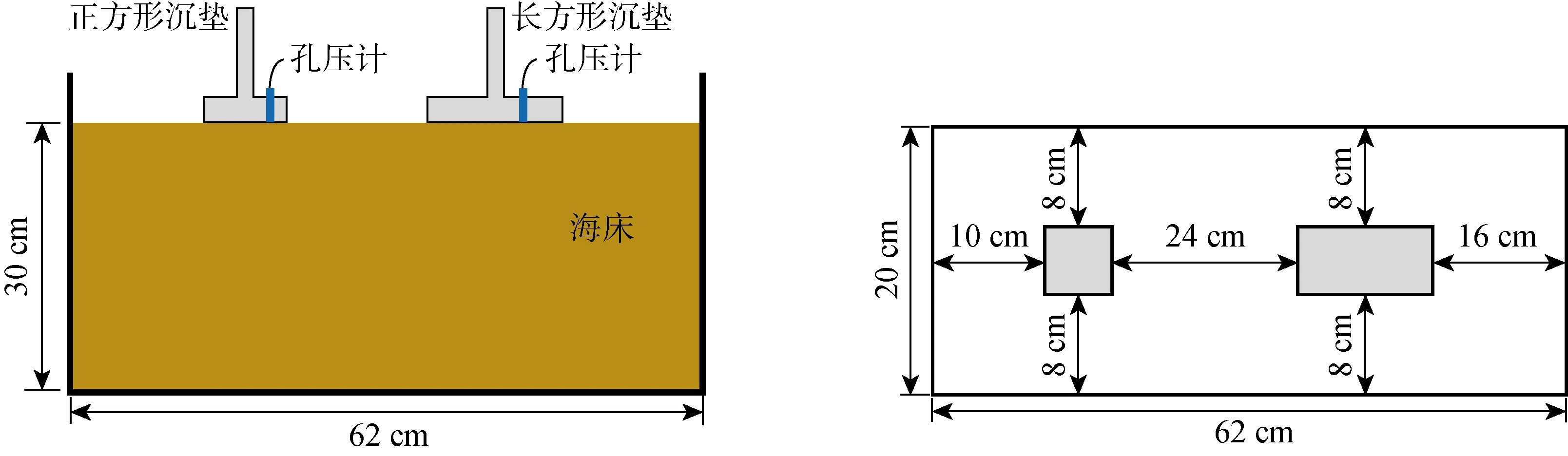
图3 试验模型布置示意图Fig.3 Schematic graphic of model layout
2 模型试验过程
离心机模型试验主要包括土体固结、土体不排水抗剪强度测量和沉垫基础承载力试验3个步骤.
2.1 土体固结
土体固结步骤为:①将土体晾干、粉碎;②过1 mm 筛,加水至饱和状态后置于搅拌机内充分搅拌混合均匀,固结土体前将硅油涂抹在模型箱内壁以降低土体与模型箱侧壁的摩擦力,减小边界效应;③在100g离心加速度下通过注浆管将泥浆注入模型箱内,4 d后完成土体固结.土体固结完成后分别制作水平和倾角为5° 的斜坡海床,如图4所示.试验用土为上海第4层海相软黏土,其物理参数如表1 所示.

表1 土样物理性质参数Tab.1 Physical property parameters of soil sample

图4 模型土体Fig.4 Model soil
2.2 土体不排水抗剪强度测试
海床土体不排水抗剪强度是影响沉垫基础竖向承载力的重要因素,因此有必要获取海床土体不排水抗剪强度的变化规律.1991年,Stewart等[15]首次在离心机中将T-bar以一定速度贯入黏土中,通过测定T-bar贯入阻力大小获取了土体强度沿深度的分布规律,此后该技术被广泛运用于测量海洋软土强度.T-bar所处排水状态[16],通过无量纲速度确定:
v*=vdT/Cv
式中:v为T-bar的贯入速度;dT为T-bar直径.当v*<0.2时,T-bar处于排水状态;当v*>20时,T-bar处于不排水状态.试验取dT=5 mm,Cv=2.04×10-9m2/s,经计算在100g离心加速度下v=1 mm/s,可测定土体的不排水抗剪强度.T-bar贯入阻力与土体不排水抗剪强度关系[15]可表示为
P=NbSudT
(1)
式中:P为T-bar单位长度受力大小;Su为土体不排水抗剪强度;Nb取决于T-bar表面的粗糙度,Stewart等[15]建议Nb取值为10.5.
2.3 沉垫基础承载力试验

(2)
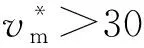
3 试验结果
3.1 试验土体强度分布规律
为更加直观反映原型,即现实中的沉垫基础情况,模型试验结果均按相似关系换算成实际结果.在水平及斜坡海床中利用T-bar进行贯入和循环试验,直到T-bar前端阻力不再随循环进一步增加,土体强度曲线如图5所示,其中d为T-bar贯入海床的深度.可知,土体不排水抗剪强度随深度的增大而增大,两者关系近似于线性分布.由于在制备5°斜坡海床的过程中用刮刀刮去了表层部分土体(最深处为5.4 cm),所以导致斜坡海床表层土体的不排水抗剪强度约为4.5 kPa.在水平海床11 m深度处,海床土体的不排水抗剪强度为22 kPa,循环弱化后土体的强度保持在6 kPa左右,对应土体灵敏度为3.7.对水平海床土体的不排水抗剪强度拟合得到其沿深度的变化规律为

图5 土体强度分布曲线Fig.5 Strength distribution of soil model
(3)
(4)
3.2 沉垫基础竖向承载力
沉垫基础在水平和斜坡海床上的荷载-位移变化曲线如图6所示,其中Q为沉垫基础所受外荷载,D为沉垫基础竖向位移.在沉垫基础的入泥过程中,竖向荷载随入泥深度的增加而增大,在加载初期荷载增长较快,后续增长速率逐渐减小且荷载-位移曲线均未出现明显的峰值,表明沉垫基础在软黏土海床上破坏模式为局部剪切破坏或冲切破坏.

图6 沉垫基础荷载-位移曲线(水平和斜坡海床)Fig.6 Load-displacement of mat-supported foundation on horizontal and sloping seabed
由于斜坡海床是在固结完成的水平海床上刮去表层部分土体后制成,所以其表层土体具有一定的超固结性,表层土体强度较高.对比正方形沉垫基础的荷载-位移曲线结果可以发现,沉垫基础在斜坡海床上的承载力明显高于水平海床.此外,由于土体不排水抗剪强度沿坡面变化,正方形基础加载位置低于长方形基础,其基础底部不排水抗剪强度也明显高于长方形基础加载位置.
3.3 孔隙水压力规律
沉垫基础入泥过程中基础底部孔隙水压力随入泥深度的变化曲线如图7所示,其中Ps为沉垫基础底部平均超孔压,斜坡海床上正方形沉垫基础底部的孔压数据由于传感器问题而未被记录.由图7可知,在沉垫基础入泥初期孔压上升较快而后续增长较缓慢,且水平海床上的超孔压初期变化比斜坡海床更大.对比图6和图7中的结果可知,土体超孔压响应与荷载的变化规律基本一致,随着入泥深度的增大而增大,沉垫基础入泥深度为1 m时,水平海床上正方形、长方形基底超孔压与对应的基础荷载分别为24.9 kPa(荷载26.7 kPa)、21.5 kPa(荷载22.47 kPa).基础竖向荷载大部分由超孔压承担,这是由于海床黏土的渗透系数较小,沉垫基础入泥速度较快,基础处于不排水条件,底部超孔压来不及消散而逐渐增大.
3.4 竖向承载力对比
目前,通常采用Vesic公式和Skempton公式计算软黏土海床上沉垫基础的极限承载力,分别为
q=SuNcKc+q0NqKq+0.5γBNγKγ
(5)
(6)
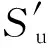

图8 基础承载力试验值与理论值比较Fig.8 Comparison of theoretical and experiment values of foundation bearing capacity
由于Skempton公式无法考虑海床坡度因素对承载力的影响,所以图8(b)未给出斜坡海床上Skempton公式的理论解.由图8可知,水平海床上Vesic公式的计算值比离心试验结果小,离心试验结果与Skempton公式计算值更加接近,这是由于Skempton公式考虑了接触面海床以下2/3B基础深度内土体的平均不排水抗剪强度,而Vesic公式采用基础-海床接触面处土体的不排水抗剪强度.以沉垫基础入泥深度达到0.25B(1 m)时的荷载作为沉垫基础的竖向承载力,水平海床上正方形沉垫基础的承载力为26.7 kPa,长方形沉垫基础的承载力为22.47 kPa,正方形基础承载力略大于长方形基础;在斜坡海床上,正方形沉垫基础的承载力为60.5 kPa,长方形沉垫基础的承载力为20.5 kPa,由于斜坡海床上正方形基础底部土体不排水抗剪强度远大于其他情况,所以基础承载力更强.
此外,由图6(b)可知,正方形基础在斜坡海床上的荷载具有明显拐点,在40 kPa后荷载增长速度明显降低,其原因可能与海床的坡度相关.图9所示为10° 斜坡海床上正方形和长方形沉垫基础的荷载-位移曲线结果,由于长方形基础距离初始泥面较近,荷载随深度变化曲线与5° 斜坡海床结果相似,但其承载力比5° 海床结果略小;正方形基础的初始加载位置比5° 海床对应的加载位置更深,加载处的土体不排水抗剪强度更大,拐点出现的位置更深,但沉垫基础入泥达1 m处的承载力仅为40 kPa左右,这是由于随海床坡度的增加,沉垫基础在斜坡海床上的破坏模式也会发生变化,进而对基础的竖向承载力产生影响.5°和10°斜坡海床试验结束后的土样情况如图10所示,可以看出正方形基础下方土体发生明显的局部滑移破坏,虽然其基础底部土体不排水抗剪强度更大,但沉垫基础承载力却小于5° 海床结果.

图9 沉垫基础荷载-位移曲线(10°海床)Fig.9 Load-displacement curves of Mat-supported foundation (10° seabed)

图10 试验后海床情况Fig.10 Seabed condition after experiment
4 竖向承载力数值分析
受离心机模型试验斜坡海床制样方法的影响,试验中斜坡海床土体表面具有一定的超固结性导致海床表层土体强度较高,与实际海床土体强度深度分布具有较大差异,为明确沉垫基础在斜坡海床上的竖向承载特性,进一步建立了数值模型并对该问题进行探讨.
4.1 数值模型建立
数值模型采用Abaqus中CEL大变形有限元方法.考虑模型的对称性,将水平海床建立1/4对称模型,斜坡海床建立1/2对称模型,沉垫基础设定为刚体,在基础上施加速度边界条件模拟基础入泥过程.海床土体采用EC3D8R欧拉体单元,海床表面以下土体的欧拉积分数EVF为1,在海床表面上设置1 m的空层(EVF为0)以捕捉土体的隆起变形.沉垫基础在加载时处于不排水状态,海床土体采用Tresca屈服准则的理想弹塑性本构模型,黏土弹性模量Es=500Su,泊松比为0.49,Su沿海床深度分布规律与试验结果相同,如式(3)所示.以10°斜坡海床为例,有限元模型如图11所示.

图11 有限元模型Fig.11 Numerical model used in this study
4.2 数值模型验证
水平海床荷载-位移曲线的数值与离心机试验结果对比如图12所示.数值与试验结果吻合较好,数值结果中正方形基础承载力比长方形基础大13%左右,而在离心机试验结果中约大18.8%,无论是数值模拟或离心机试验结果两者的荷载-位移曲线都无明显拐点,数值结果与离心机试验结果曲线形态一致.

图12 数值结果与离心机试验结果对比Fig.12 Comparison of numerical calculation with centrifuge test
4.3 斜坡海床竖向承载特性
沉垫基础在不同斜坡海床上的荷载-位移曲线如图13所示.基础承载力随海床坡度的增大而逐渐减小,海床角度从0°增至10°时,正方形和长方形沉垫基础的承载力分别减小了17.1%和23.8%.受土体不排水抗剪强度分布影响,在0.2 m内曲线斜率变化较为缓慢,0.2 m后曲线斜率变化明显,随着基础入土深度增加,荷载差别逐渐增大.此外,长方形沉垫基础对10°斜坡海床的作用力比正方形更大,从而导致基础底部土体发生部分滑移,与离心机试验结果呈相似现象.

图13 不同坡度海床上基础承载力曲线Fig.13 Bearing capacity of seabed foundation with different slopes
数值计算结果与离心机试验及经验公式计算结果的对比如图14所示,其中α为海床斜坡角度,水平海床和斜坡海床土体抗剪强度分布规律均与式(3)一致.水平海床中数值结果与试验结果吻合较好,虽然10°斜坡海床上长方形基础的承载力数值结果均略大于公式计算结果,但随着海床坡度增大两者的差距正逐渐减小.在10°斜坡海床上长方形基础发生滑移现象而导致承载力更低,因此在实际工程中应谨慎考虑海床坡度对基础承载力的影响.
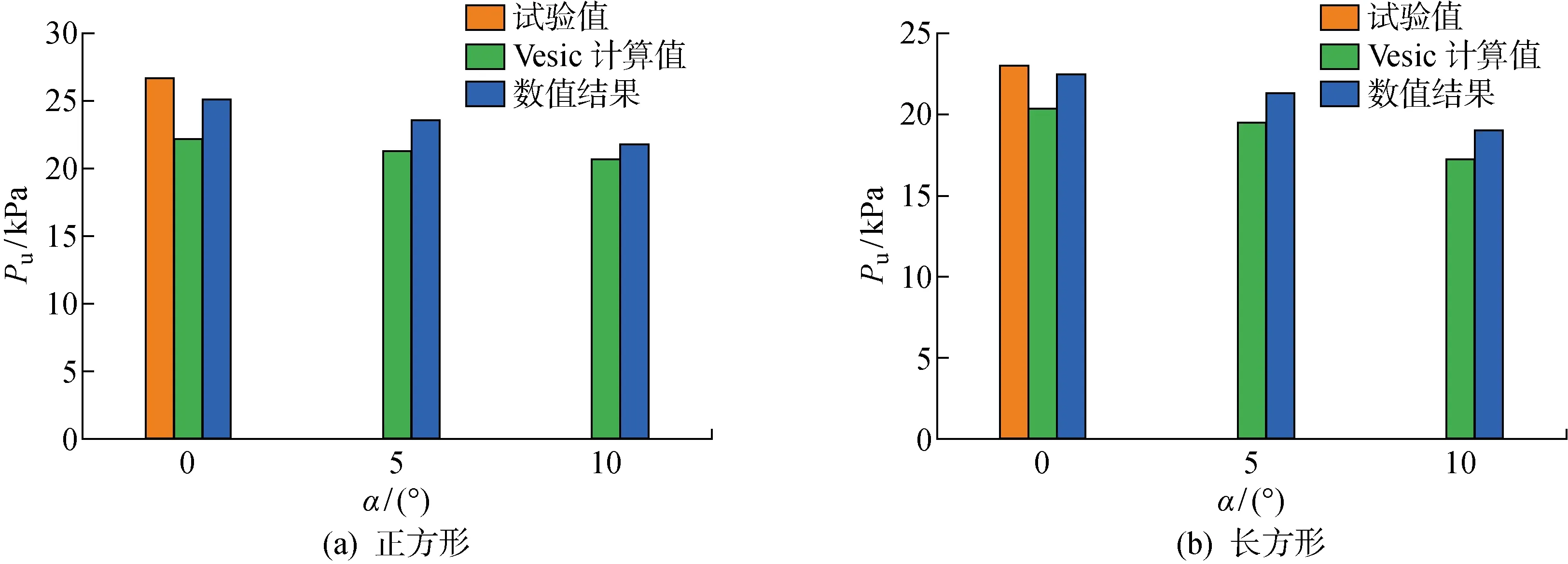
图14 不同坡度海床上基础承载力对比Fig.14 Comparison of foundation bearing capacity on seabed with different slopes
海床土体在沉垫基础作用下的位移矢量图如图15所示.在基础压入过程中0°和5°海床土体被挤出并在基础两侧形成隆起,随着海床坡度逐渐增大土体流动机制有明显不同, 正方形和长方形基础下方土体均有向坡脚方向的滑移趋势,在图15(c)和图15(f)的10°斜坡海床中,在正方形与长方形沉垫基础作用下,海床土体的最大水平位移分别达到了0.65、3 m,位于长方形基础下方的海床土体有明显滑动位移,因而对基础竖向承载力产生较大影响.
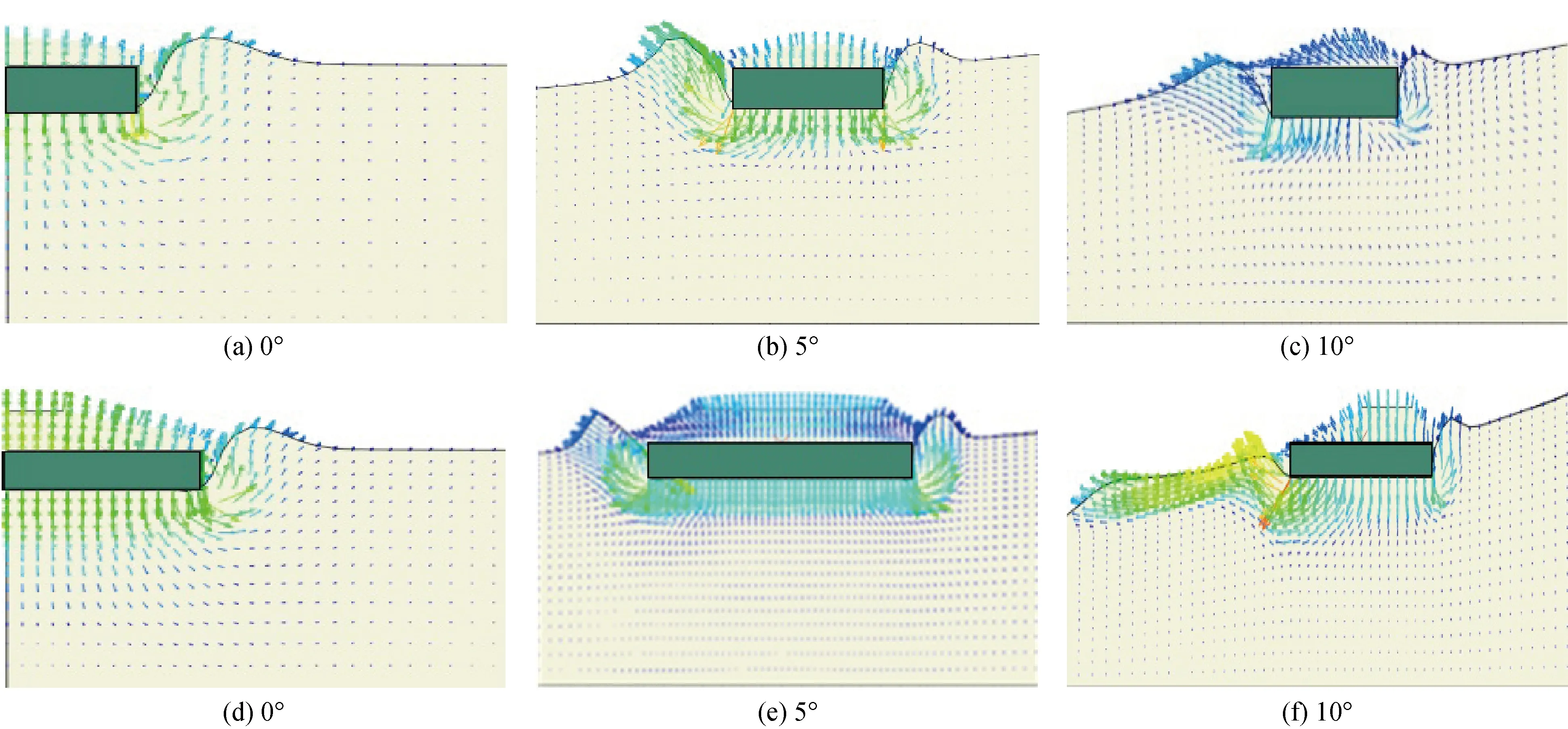
图15 海床位移矢量图(a~c正方形基础,d~f长方形基础)Fig.15 Sketch of displacement vectors of seabed (a—c square foundation, d—f rectangle foundation)
离心机模型试验和数值结果表明沉垫基础形状和海床坡度对基础承载力都有影响,但海床坡度的影响更加显著,随着海床坡度的增加基础破坏模式发生变化,海床坡度过大时可能发生滑移破坏,因此实际工程中应尽量避免沉垫基础坐底在斜坡较大的海床上,且设计时应考虑海床坡度对基础承载力的削弱作用.
5 结论
通过离心机模型试验和数值方法研究沉垫基础在水平和斜坡海床上的竖向承载力特性,主要结论如下.

(2) 沉垫基础入泥过程中土体孔隙水压力的发展规律与基础荷载-位移曲线变化规律基本一致,黏土渗透性差导致超孔压消散缓慢,竖向应力大部分由超孔压承担.
(3) 沉垫基础竖向承载力随入泥深度的增加而增加,荷载-位移曲线没有明显峰值,水平海床上正方形沉垫基础承载力大于长方形基础,随着海床坡度的增加土体位移流动机制发生变化,10°斜坡海床下基础发生滑移现象而导致承载力更低.
(4) 采用CEL大变形有限元分析方法能较为准确地模拟沉垫基础入泥过程,沉垫基础竖向承载力略大于公式计算结果,但当斜坡海床角度过大时,公式计算结果会高估基础承载力,在设计时应考虑海床坡度对基础承载力的削弱作用.

