带有尾缘襟翼的兆瓦级大型垂直轴风力机气动性能优化
陈 昊, 戴孟祎, 韩兆龙,2,3,4, 周 岱,2,3, 包 艳,2,3, 涂佳黄
(1.上海交通大学 船舶海洋与建筑工程学院; 海洋工程国家重点实验室,上海 200240;2.上海交通大学 水动力学教育部重点实验室,上海 200240; 3.上海交通大学 上海市公共建筑和基础设施数字化运维重点实验室,上海 200240; 4.上海交通大学 极地深海技术研究院;海洋装备研究院,上海 200240; 5.湘潭大学 土木工程与力学学院,湖南 湘潭 411105)
全球人口的不断增长和对未来可持续发展的要求将导致对清洁能源需求的大幅提升.风能相比于其他可再生资源,在陆上和海上都有着丰富的储量,同时,风能发电技术也在不断进步和发展,未来风能将有望成为最具前景的新能源形式[1-2].而风力机作为捕获风能最重要的装置,其构型对风能的利用率有直接影响.现代风力机根据旋转轴方向不同,主要包括垂直轴风力机(VAWT)和水平轴风力机[3].水平轴风力机以其更高的风能利用率和更成熟的技术是目前使用最广泛的风力机.但在水平轴风力机发展的过程中,其固有缺陷也逐渐暴露,主要包括以下几个方面:①叶片质量过大引起展向荷载疲劳,不利于风力机的大型化发展;②发电机组重心过高,不仅使得风力机稳定性面临挑战,也使安装和维护成本变高;③需要偏航装置.而随着风资源的不断开发利用,垂直轴风力机在结构形式、风场集群效应以及大型化等方面的优势正受到越来越多的关注[4-5].根据计算可知,垂直轴风力机的最大发电容量能够达到30 MW左右,这表明垂直轴风力机在兆瓦级的大型风力机应用上具有巨大潜力[6].
目前,低风能利用率是限制垂直轴风力机发展的主要原因,一方面是由于在叶片旋转过程中,上风区叶片会不断产生脱落涡,且来流在经过上风区后速度会有明显的亏损,导致下风区叶片无法对风能进行有效提取;另一方面,叶片攻角周期性大幅变化将导致叶片的动态失速以及叶片周围复杂的非稳态流动[7].为了能够充分发挥垂直轴风力机的优势,有必要对其气动性能优化展开研究[8].
在实际应用中,桨距和襟翼控制是延缓风力机叶片动态失速、提高风能利用率的主要手段.对于桨距控制而言,Chen等[9]比较了固定桨距和变桨距垂直轴风力机的性能,后者的叶片在旋转过程中被迫做正弦俯仰运动.结果表明,无论是功率输出、转速还是转矩输出方面的波动都得到了抑制,同时风力机的效率也得到了提高.Abdalrahman等[10]提出了一种基于多层感知机神经网络的智能控制技术,用于设计H型垂直轴风力机的单个叶片主动桨距控制系统,以提高其发电性能.与传统控制方法相比,基于多层感知机神经网络的叶片桨距控制系统对H型垂直轴风力机的功率输出产生了显著改善.Li等[11]构建了由遗传算法和计算流体动力学(CFD)仿真模块组成的变桨距自动优化平台(VBPAOP),以搜索能够最大化垂直轴风力机功率的最佳桨距.研究结果表明,在较宽的叶尖速比范围内,优化后的桨距角使两种不同弦长的垂直轴风力机的平均功率系数都得到了提升.在低叶尖速比阶段,最佳桨距角控制有效缓解了由于动态失速而导致的转矩损失.而在高叶尖速比阶段,由于上风区尾流速度的增加而改善了下风区叶片的气动性能.对于襟翼控制而言,季康等[12]设计了基于NACA 0012翼型的襟翼翼型,运用CFD数值模拟方法,得到了风力机在运行时的气动参数.研究结果表明,通过改变叶片在不同方位角下的襟翼摆角,可以有效抑制叶片表面的流动分离并降低风力机的气动荷载波动,从而达到改善垂直轴风力机的气动性能并延长其使用寿命的目的.叶舟等[13]基于遗传算法建立了尾缘襟翼优化模型,将升阻比和升力系数之和作为目标函数,对襟翼的摆角进行优化,并运用CFD数值模拟方法分析了叶片周围的流场特性.研究结果表明,优化后带有尾缘襟翼的翼型升阻比增加了16%,升力系数增加了10.1%.
然而,上述研究主要针对小型风力机.对于兆瓦级大型垂直轴风力机,一方面,单纯采用变桨距控制需要耗费较多的外部能量,且在控制桨距运动时需要更长的响应时间;另一方面,当叶片在旋转过程中攻角过大时,仅采用尾缘襟翼控制对调整叶片攻角的作用有限.
提出一种新型的桨距和襟翼协同运动下的垂直轴风力机模型,以改善传统垂直轴风力机的气动性能.在建立CFD数值模型的基础上,验证了桨距和襟翼的协同控制在大型垂直风力机上的应用价值,将考虑桨距和襟翼运动后的模型与原始模型进行对比,从功率系数、气动力系数、流场参数和静压分布等方面研究了桨距和襟翼协同运动下的垂直轴风力机气动特性.
1 计算模型及方法
介绍垂直轴风力机模型的几何参数、CFD计算域和边界条件、网格和数值模型参数的设置,从而保证CFD数值模拟计算结果的准确性.
1.1 几何模型
表1给出了垂直轴风力机模型的主要几何参数,该原始模型以文献[14]中的小型垂直轴风力机模型为基础按照1∶50的比例放大后获得,功率约为0.65 MW.在考虑风力机尺寸缩放时,一般而言,随着叶片和旋转半径的几何相似性放大,最基本的相似原则是保持风力机的叶尖速比不变,从而保持叶片表面气体流动的几何特性不变,即叶片的攻角和周围的局部风速不会发生变化.因此,在本研究中,大型垂直轴风力机的叶尖速比与原始小型垂直轴风力机中的叶尖速比保持一致.此外,考虑计算效率,而不考虑支撑杆和转轴对风力机整体性能的影响.相关研究[14-15]表明,由于支撑杆摩擦而导致的风力机性能损失可以达到20%左右,特别是在高叶尖速比下,这一损失将更为明显.然而,对于优化截面后的支撑杆,例如采用NACA 0021翼型的支撑杆,其对风力机整体性能造成的损失将大大降低[16].
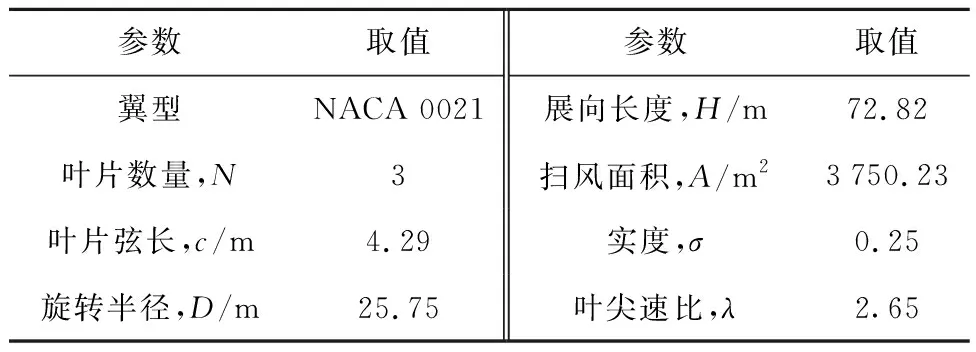
表1 垂直轴风力机模型的几何参数Tab.1 Geometric properties of VAWT model
图1为带有尾缘襟翼的垂直轴风力机示意图.图中,ω和R分别为角速度和旋转半径,Fth和Fla分别为叶片所受到的推力和侧向力.假定风力机下风区风速和上风区的自由来流速度相同[15],即诱导速度为0.因此,相对局部速度可表示为
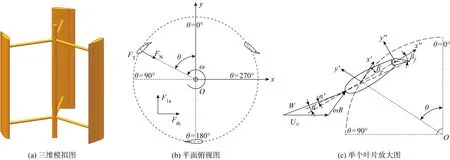
图1 带有尾缘襟翼的垂直轴风力机示意图Fig.1 Schematic diagram of VAWT with trailing edge flaps
(1)
式中:U∞为自由来流速度;θ为叶片所在方位角.
叶片攻角为叶片位置的相对局部速度与叶片弦线之间的夹角,即:
(2)
考虑桨距和襟翼的运动都会对叶片的原始攻角产生影响,即产生附加桨距攻角和附加襟翼攻角,因此,桨距和襟翼协同运动下的叶片攻角可以重新表示为
(3)
式中:xp为叶片前缘到桨距旋转中心的距离;xf为叶片前缘到襟翼旋转中心的距离;在本研究中xp=0.25c,xf=0.95c;βp(θ)和βf(θ)分别为桨距和襟翼的运动函数.
为了研究作用于叶片上的气动力,选取几个关键气动力参数进行研究.其中,切向力FT和法向力FN的方向如图1(b)中所示,切向力系数CT和法向力系数CN可表示为
(4)
(5)
式中:ρ为空气密度.
利用转矩系数CQ、功率系数CP、推力系数Cth和侧向力系数Cla可以对风力机的气动性能进行评价,风力机的转矩系数和功率系数可以表示为
(6)
(7)
式中:Q为风力机转矩.
推力系数和侧向力系数可以表示为
(8)
(9)
1.2 CFD计算域和边界条件
如图2所示,在几何模型的基础上建立了三维CFD计算域以进行数值模拟.整个计算域主要由8个区域组成,即桨距运动区域P1~P3、襟翼运动区域F1~F3、风力机的旋转域和背景区域.区域P1~P3和F1~F3是围绕叶片的圆形可旋转子域,通过旋转重叠网格区域模拟桨距和襟翼的运动,以避免重复建模过程,通过滑动网格模拟风力机的旋转运动.此外,对襟翼周围和风力机尾流区域进行了细化,以保证计算的准确.从入口边界到风力机中心的距离为5D,计算域的总宽度设置为10D,出口位于风力机中心下游15D,从而保证尾流充分发展.叶片底部距离地面的距离为1/2H,计算域的总高度为5H.对于边界条件的设置,参考文献[14]中将流场的上游侧设置为入口边界条件,均匀来流速度U∞= 9 m/s,而流场下游侧设置为出口条件,出口的相对压力为Pout= 0,空气密度为ρ=1.225 kg/m3,入口湍流强度为I=5%.
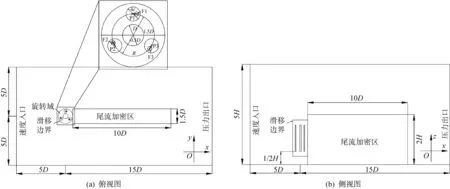
图2 CFD计算域和边界条件示意图Fig.2 Schematic diagram of computational domain and boundary
1.3 网格设置
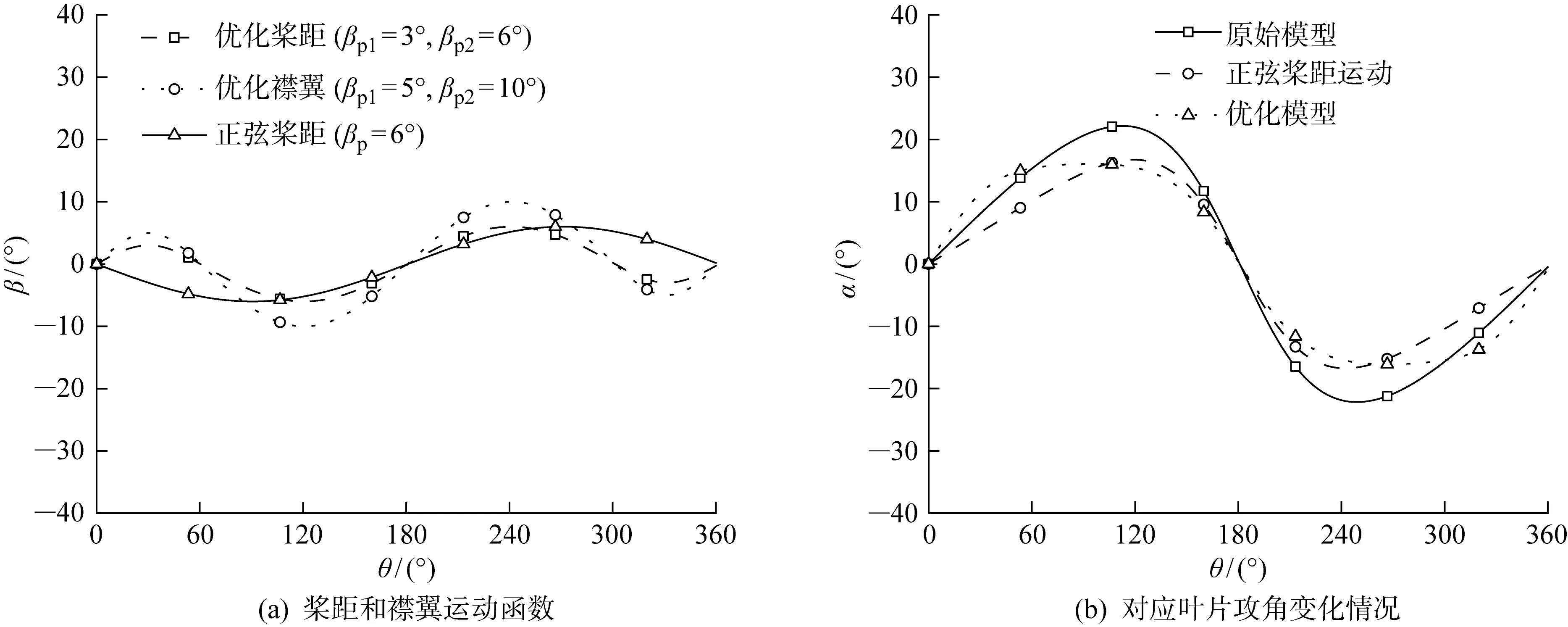
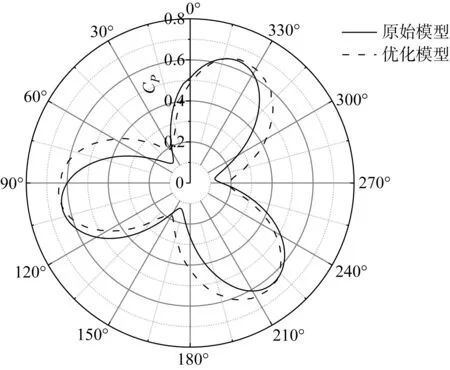
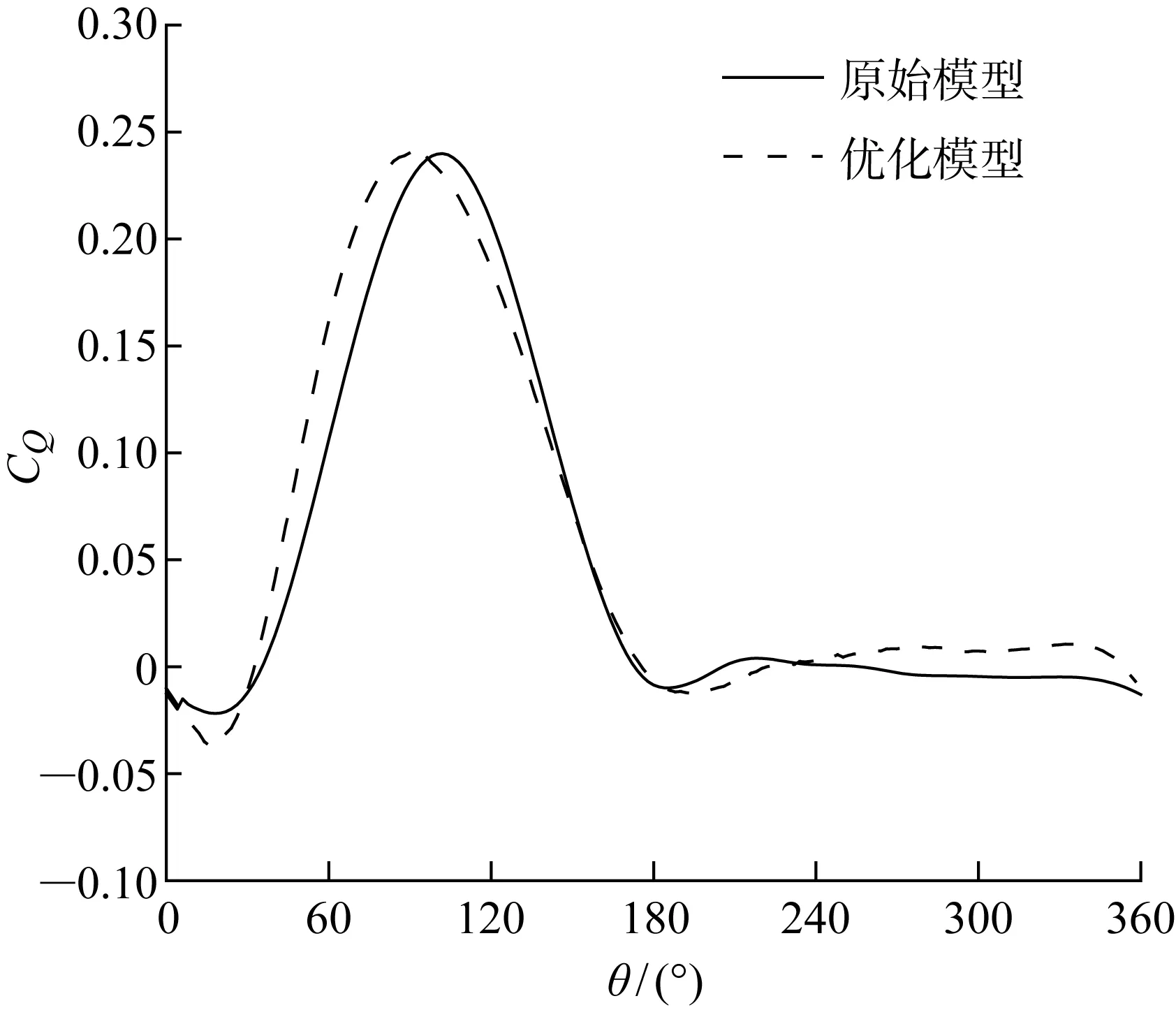
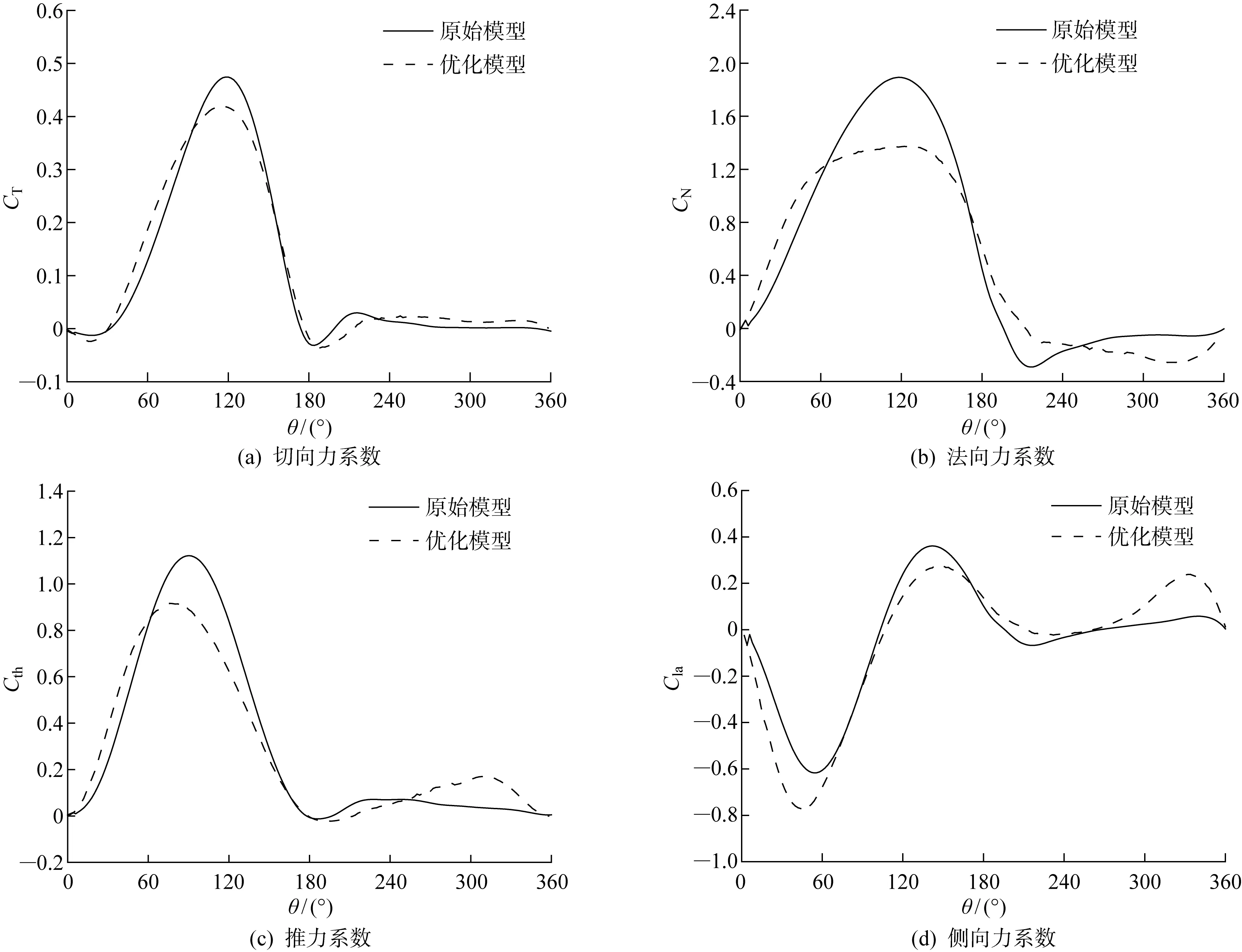
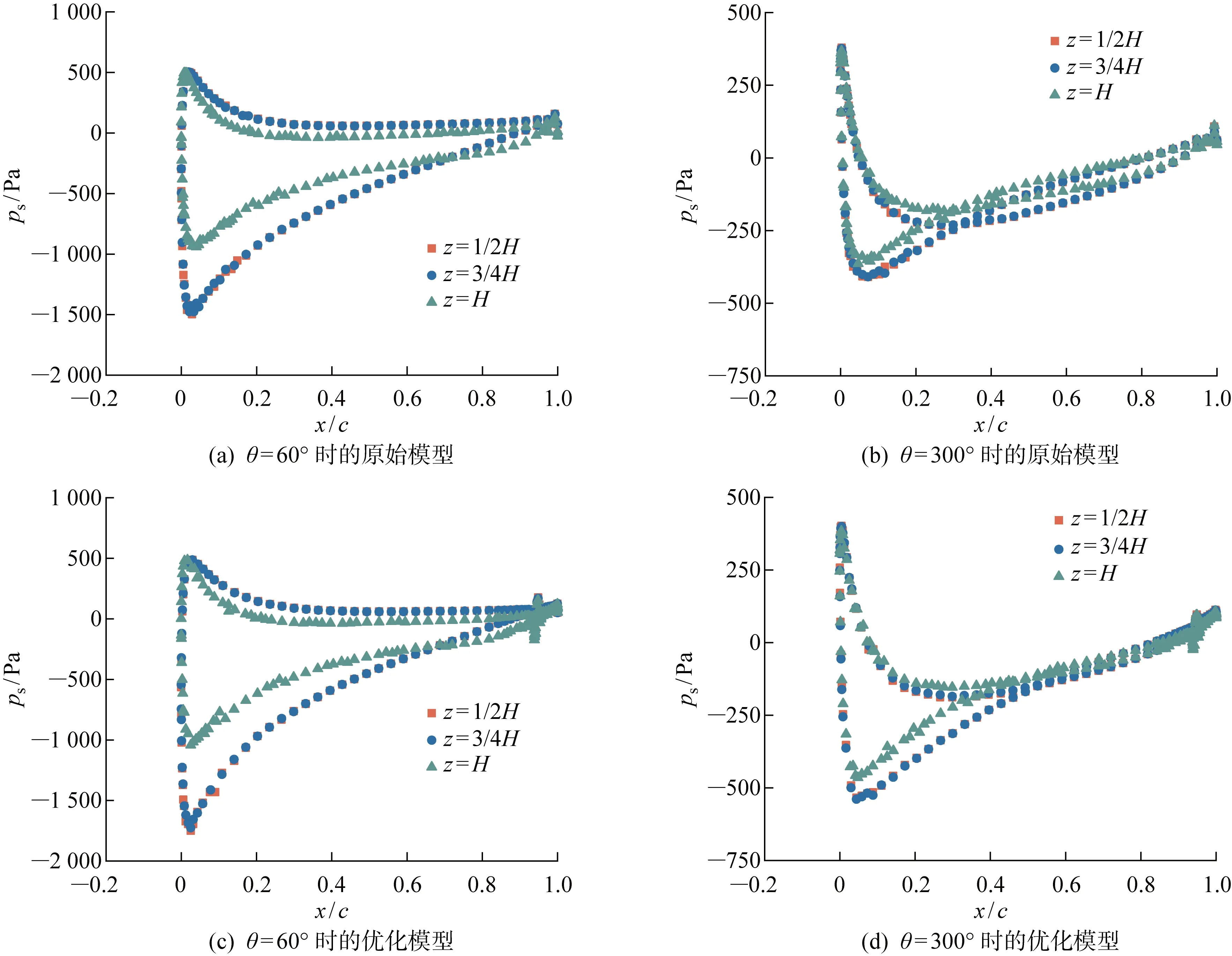
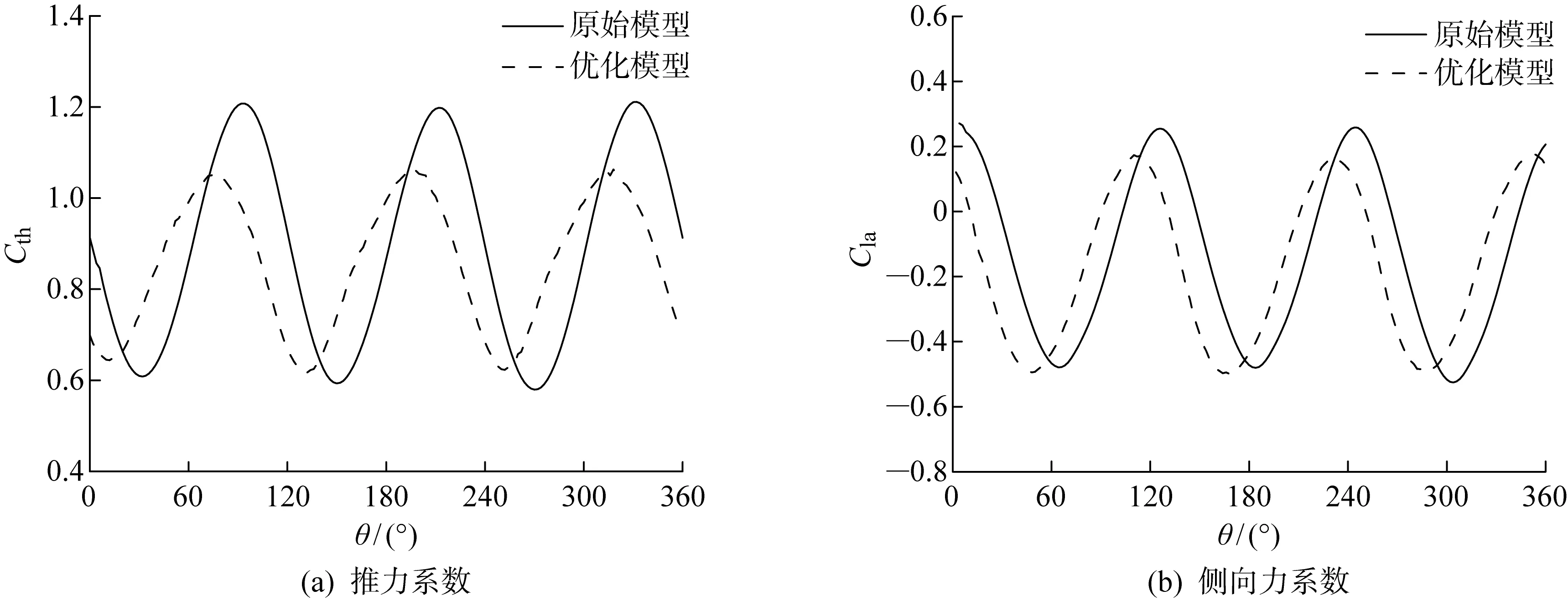
为精确分析风力机的气动性能,整体计算域和叶片表面的棱柱层网格如图3所示,棱柱层的总厚度为480 mm,增长率为1.1,层数为28层.基于来流风速为9 m/s,弦长为4.29 m,可以推算出雷诺数变化范围大约为4×106~9×106.采用基于有限体积法的软件STAR-CCM+中具有混合壁面函数的全y+处理,针对此类壁面函数处理,一般保证壁面y+<1或壁面y+>30即可.本研究中的计算模型壁面50 图3 计算网格的拓扑结构图Fig.3 Topology diagram of grid 网格独立性验证以及与实验结果的对比已经在既往研究中获得结果[17],由于目前暂无相同尺度大小的垂直轴风力机实验数据,所以本研究采用小型垂直轴风力机的原始模型对其进行有效性验证,从而验证SSTk-ω湍流模型对此类问题的适用性.另一方面,由于带有尾缘襟翼的翼型是在原始模型基础上建立的,两者仅仅在翼型的尾缘处有所差异,所以对尾缘处的网格进行了局部加密,从而确保数值模拟结果的准确性.该优化模型对高叶尖速比下的功率系数有所高估,这主要是由于忽略了叶片支撑杠和转轴;对于低到中等高叶尖速比,计算的功率系数相对于实验数据较低.总体来看,数值模拟的功率系数和实验结果基本一致.在此基础上,将采用相同的数值模拟方法和设置进行研究. 湍流模型的选择对数值模拟的精度和计算效率有很大影响.对于垂直轴风力机而言,叶片附近从层流到湍流的转捩、流动分离和再附着等均选择最合适湍流模型时需要考虑的因素.采用STAR-CCM+软件对三维非定常不可压缩流动进行数值模拟.采用SSTk-ω湍流模型求解纳维-斯托克斯(Navier-Stokes, N-S)方程,SSTk-ω模型的稳定性和可靠性已在风力机的数值模拟中得到了广泛验证[18-20].对流项采用二阶迎风格式,时间离散采用二阶中心差分格式.采用压力耦合方程组的半隐式算法(SIMPLE)耦合压力-速度方程[20]. 对于周期性非定常计算,时间步长和内迭代次数对计算的收敛性和稳定性至关重要.设置时间步为T/180(T为风力机旋转周期),内迭代次数为20次[21-22].对于本研究中的数值模型,相邻周期转矩的峰值在20个周期后几乎不再变化(相对误差小于1%).因此,所有的数据都将在第20圈时进行采样. 实际工程中将采用机械装置对桨距和襟翼的运动进行主动控制,而在本研究中采用STAR-CCM+中的用户自定义函数对桨距和襟翼的运动进行控制(见图1(c)),分别在桨距旋转中心和襟翼旋转中心处建立局部坐标系,叶片桨距和襟翼均可绕其各自的旋转中心进行运动.此外,所有坐标系都是右手坐标系,桨距角βp和襟翼偏转角βf以逆时针为正,确保风力机的桨距和襟翼按照给定函数进行运动. 图4(a)为叶片桨距和襟翼在叶尖速比为2.65时的运动曲线和对应的叶片理论攻角变化.在0° ≤θ<60° 时,桨距和襟翼逆时针旋转以增大叶片的升力;在60° ≤θ<180° 时,桨距和襟翼顺时针旋转,减小攻角以缓解动态失速.在风力机旋转的后半圈(180° ≤θ<360°),桨距和襟翼的旋转方向与前半圈(0° ≤θ<180°)恰好相反.此外,在0° ≤θ<60° 和300° ≤θ<360° 时,桨距和襟翼的最大振幅βp1、βf1为当60° ≤θ<180° 和180° ≤θ<300° 时桨距和襟翼最大振幅βp2、βf2的一半,从而确保桨距和襟翼速度变化的连续性. 图4 桨距和襟翼运动策略Fig.4 Strategy of pitch and flap motion 桨距和襟翼振幅关于方位角θ的运动函数如下所示: βp(θ)= (10) βf(θ)= (11) 式中:βp1= 3°,βp2= 6°,βp1= 5°,βp2= 10°. 风力机的气动载荷是衡量其气动性能的主要参数,本文主要通过与原始垂直轴风力机模型对比,分析桨距和襟翼运动对单个叶片和整机气动特性的影响. 图5为原始模型与考虑桨距和襟翼协同运动下的模型在一个旋转周期内的瞬时功率系数对比.可以发现,桨距和襟翼协同运动下的模型相比于原始模型虽然峰值功率系数没有明显改善,但最低功率系数却显著提高,从0.123变为0.166,提高了35%.此外,可以发现,桨距和襟翼协同运动下的整体瞬时功率系数曲线的相位角相比于原始模型具有一定提前,这是由于桨距和襟翼的运动对叶片的攻角起到了调整作用,使得叶片在旋转过程中最大攻角出现的位置更加提前. 图5 瞬时功率系数对比Fig.5 Comparison of instantaneous power coefficient 图6为相同翼型下的小型垂直轴风力机原始模型和大型垂直轴风力机优化前后平均功率系数的对比情况.相比于小型风力机,原始大型风力机的功率系数较高,这是由于大型风力机的雷诺数比小型风力机高1~2个数量级,一般雷诺数越高,翼型的气动性能也越好,更不容易发生边界层分离[23-25].在优化前,风力机的功率系数为0.386,功率约为0.65 MW,而在优化后风力机的功率系数为0.433,功率约为0.73 MW,其中功率系数提升了12.2%. 图6 小型和大型垂直轴风力机平均功率系数对比Fig.6 Comparison of average power coefficient between small and large VAWT 图7为不同方位角下的转矩系数对比.从图中可以看出,优化模型相比于原始模型的性能提高主要是在30° <θ<90° 和240° <θ<360° 这两个区间内,这是由于在这两个区间内,桨距和襟翼的运动增大了叶片的有效攻角,使得叶片的升阻比可以快速提升.然而对于中等叶尖速比下的垂直轴风力机,叶片在旋转过程中的攻角较小,不会出现严重的动态失速,其本身的气动性能较优[26],因此在 120° <θ<240° 范围内的提升效果比较有限. 图7 不同方位角下的转矩系数对比Fig.7 Comparison of torque coefficient at different azimuth angles 图8对比了单个叶片在不同方位角下的不同力系数,图8(a)和8(b)分别为叶片的切向力和法向力系数对比.与叶片的转矩系数曲线类似,在30° <θ<90° 和240° <θ<360° 这两个范围内,优化模型的切向力系数要明显高于原始模型,这也解释了在这一范围内优化模型的转矩系数要高于原始模型的原因.从叶片的法向力系数对比中可以发现,在 60° <θ<180° 范围内,优化模型的法向力系数明显低于原始模型,最大法向力系数从1.89降低到1.36,减少了28.04%,而这将大大降低风力机在旋转过程中叶片支撑杆所受到的荷载.图8(c)和8(d)分别为单个叶片的推力和侧向力系数对比.在0° <θ<60° 和240° <θ<360° 范围内,优化模型的推力和侧向力系数均高于原始模型,而在60° <θ<180° 范围内,优化模型低于原始模型,与转矩系数曲线的变化基本一致. 图8 不同方位角下的单个叶片力系数对比Fig.8 Comparison of force coefficients of single blade at different azimuth angles 为进一步分析桨距和襟翼协同运动下的叶片在30° <θ<90° 和240° <θ<360° 这两个范围内气动性能较优的原因,对叶片附近的流场和叶片表面静压分布进行分析. 图9显示了优化模型在叶片周围的速度场分布,可以发现优化模型在叶片前缘位置处的速度值明显高于原始模型,而局部速度的增加会造成压力降低.从图10叶片周围的压力场分布也可以发现,优化模型在吸力面叶片前缘的负压比原始模型更大,从而加大了吸力面和压力面之间的压差,这也进一步解释了叶片在这一方位角的切向力和转矩系数提升的原因. 图11显示了60° 和300° 方位角下原始模型和优化模型的叶片在不同截面处的静压(ps)分布.可以看到,无论是原始模型还是优化模型,在叶片截面z=1/2H处和z=3/4H处的压力分布基本相同,然而在z=H处,叶片前缘位置处的负压明显升高.这是由于叶片沿展向长度的有限性,在压差推动下压力面的气流将绕过叶尖进入吸力面形成叶尖涡.由于叶尖涡效应,叶片在叶尖处的边界层更厚,也更容易发生流动分离,从而导致叶片上下表面的压差减少,这也是图中负压升高的主要原因.此外,对比图11(a)和11(c)以及图11(b)和11(d),原始模型和优化模型在叶片前缘的正压力几乎相同,但考虑桨距和襟翼运动下的叶片的负压要明显低于原始模型.当方位角为60° 时,原始模型的最大负压为-1 500 Pa,优化模型的最大负压为-1 750 Pa;当方位角为300°时,原始模型的最大负压为-400 Pa,优化模型的最大负压为-540 Pa.一般来说,叶片前缘的压差越大,叶片产生的气动力也越大.因此,在30° <θ<90° 和240° <θ<360° 这两个范围内,考虑桨距和襟翼运动下叶片的有效压差要高于原始模型,从而能够为叶片提供更大的升力,而这也是其气动性能优于原始模型的原因. 图11 叶片不同截面处的静压分布对比Fig.11 Comparison of static pressure distributions in different blade sections 叶片周期性转动将导致整机受到周期性荷载,对于大型垂直轴风力机而言,这些荷载不容忽视,也会影响风力机的使用寿命.图12(a)和图12(b)分别为整机的推力系数和侧向力系数对比.结果表明,优化模型的侧向力和推力相较于原始模型都有明显降低,最大推力系数绝对值从1.21降低到1.06,最大侧向力系数绝对值从0.53降低到0.49,分别减少了12.4%和7.5%.整机的侧向力和推力的波动幅值皆明显低于原始模型,这将有助于降低作用在风力机整机上的疲劳荷载. 图12 整机力系数对比Fig.12 Comparison of force coefficients of VAWT 采用SSTk-ω湍流模型对带有尾缘襟翼的兆瓦级大型垂直轴风力机气动性能进行CFD数值研究.通过对比原始模型与考虑桨距和襟翼协同运动模型的功率系数、单叶片力系数、叶片附近流动参数、静压分布、整机荷载等结果,发现桨距和襟翼的协同运动可以提高风力机的风能转换率,降低气动荷载,主要研究结果如下: (1) 考虑桨距和襟翼协同运动的模型可以显著提高大型垂直轴风力机的功率系数.与原始模型相比,功率系数提高了12.2%,其性能提高主要是在30° <θ<90° 和240° <θ<360° 这两个范围内. (2) 考虑桨距和襟翼协同运动下的模型影响了叶片表面的静压分布.原始模型和优化模型在叶片前缘的正压力几乎相同,但考虑桨距和襟翼运动的叶片的负压在30° <θ<90° 和240° <θ<360° 范围内明显低于原始模型,从而能够为叶片提供更大的升力,而这也是其气动性能优于原始模型的原因. (3) 桨距和襟翼的协同运动显著降低了风力机整体受到的荷载.与原始模型相比,整机最大推力系数绝对值和最大侧向力系数绝对值分别减少12.4%和7.5%,推力和侧向力波动幅值的降低将有助于降低风力机上的周期性疲劳荷载.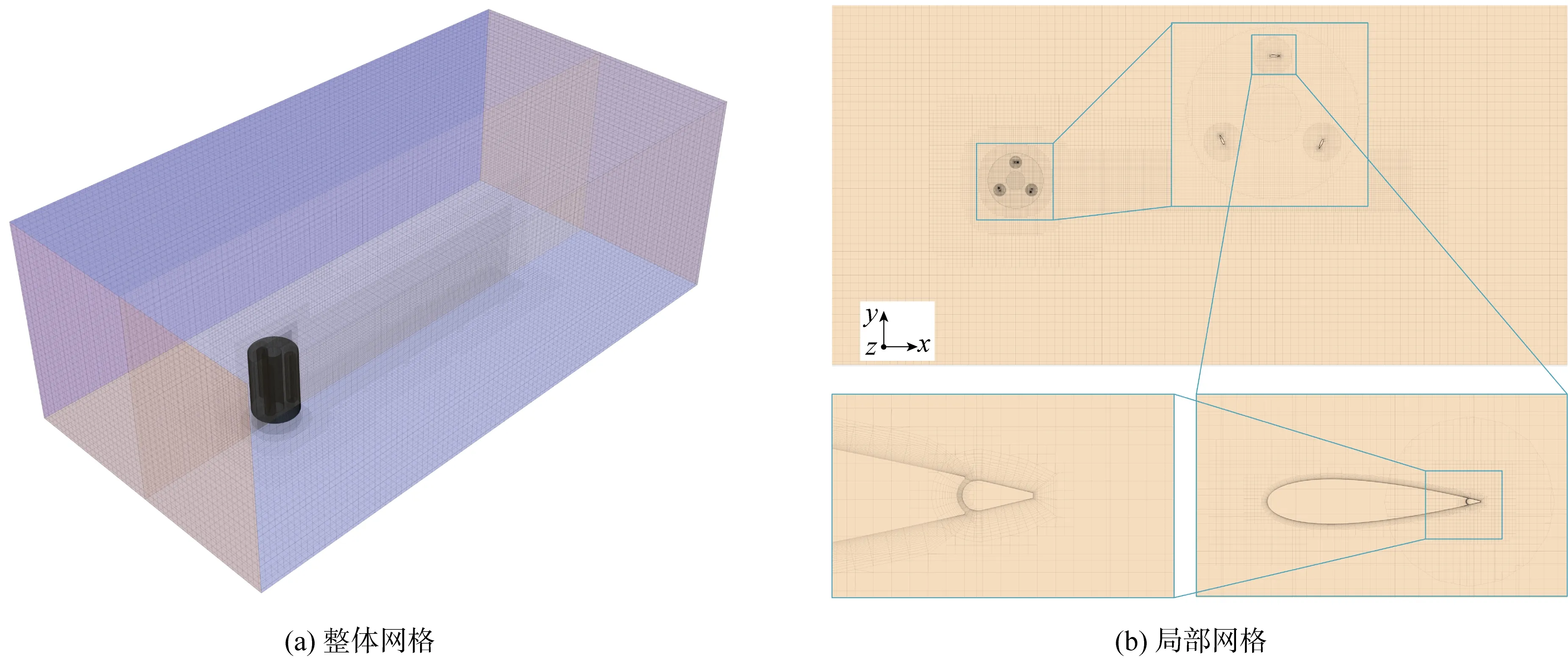
1.4 数值设置
2 桨距和襟翼运动策略
3 结果与分析
3.1 气动特性分析

3.2 流场和静压分布
3.3 整机荷载分析
4 结论

