『比』的应用

◎周 楠

“比”在数学中应用十分广泛，我们可以运用“比”的基本性质把比转化成分数来解决相应的数学问题。

【例1】甲、乙两种商品的价格比是5∶3。如果它们的价格分别上涨了420 元后，价格比变为6∶5，那么甲、乙两种商品原来的价格各是多少元？

【思路分析】根据条件“甲、乙两种商品分别上涨了420 元”，可知它们的价格差是不变的。由甲、乙两种商品原来的价格比是5∶3，可以知道它们的价格差是5-3=2（份）。而现在的价格比是6∶5，价格差却是6-5=1（份）。要使差不变，6∶5 的前项和后项应该分别乘2÷1=2，即（6×2）∶（5×2）=12∶10。420 元就是这样的12-5=7（份），每一份就是420÷7=60（元），甲原来有5份，就是60×5=300（元），乙原来有3份，就是60×3=180（元）。

解：5-3=2（份），6-5=1（份），2÷1=2，（6×2）∶（5×2）=12∶10

12-5=7 （份）或10-3=7 （份），420÷7=60（元），60×5=300（元），60×3=180（元）

答：甲商品原来的价格是300元，乙商品原来的价格是180元。

还可以列方程解答。

解：设原来甲有5x元，乙有3x元。

答：甲商品原来的价格是300元，乙商品原来的价格是180元。

【例2】操场上有一些学生在玩游戏，其中男生人数与女生人数的比是4∶3，后来从教室里走出来2名女生加入，这时男生人数与女生人数的比是5∶4。原来有男、女生各多少名？

【思路分析】根据条件，女生人数发生了变化，总人数也发生了变化，但男生人数没有变。因此可以把男生人数看作单位“1”。根据“男生人数与女生人数的比是4∶3”，可知女生人数占男生人数的。根据“从教室里走出来2 名女生加入，这时男生人数与女生人数的比是5∶4”，可知这时女生人数占男生人数的，即后来的2名女生人数占男生人数的，由此可以求出男生人数。

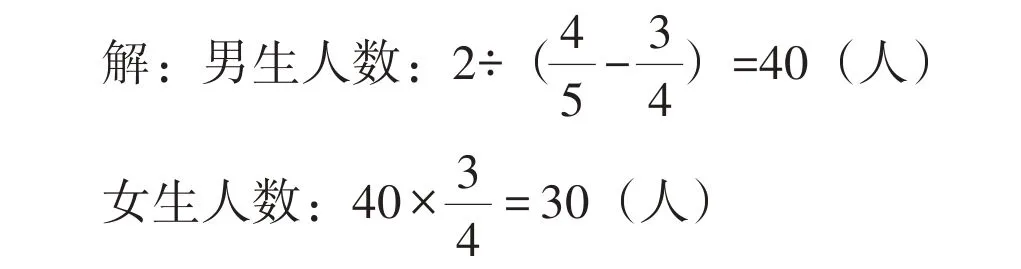
答：原来男生有40人，女生有30人。

【挑战自我】三箱水果共重180 千克。如果从第一、二箱中分别取出3 千克水果放入第三箱中，则第一、二、三箱水果的质量比是2∶3∶4。三箱水果原来分别有多少千克？

（扫二维码可见答案，扫码仅需一元）