基于正交结果分析的内镶贴片式滴灌带性能优化设计

陶洪飞，刘 姚，陶娟琴，周 良，李 巧，马合木江·艾合买提，姜有为

（1.新疆农业大学 水利与土木工程学院，乌鲁木齐 830052；2.新疆水利工程安全与水灾害防治重点实验室，乌鲁木齐 830052；3.中建新疆建工，成都 610000）

0 引 言1

【研究意义】我国是农业大国，农业用水量占总用水量的比例较大，水资源短缺制约着经济发展和农业生产，大力推进我国农业节水灌溉发展，可以从根本上缓解我国农业缺水的问题[1]。近年来，滴灌技术在新疆得到广泛使用，大部分地区的灌溉水源主要来源于山区的降水径流和冰川融雪等含沙量较高的地表水。含沙水作为滴灌灌溉水源的最大弊端就是导致灌水器的严重堵塞,同时由于滴灌带的进水口和出水口都很小，极易受含沙水的影响，使得灌溉系统无法正常运行[2-4]。目前为了减缓泥沙带来的灌水器堵塞问题，部分会采用修建沉砂池或者配备过滤器，但是这会使得成本大幅增加，实际上选用滴灌灌水器将降低对系统沉降和过滤的要求。滴灌效率受灌溉水质、流道结构、工作压力等因素的影响，灌水器的堵塞无法避免，即使是在灌溉水质较好且过滤设施完备的情况下，灌溉系统也会出现堵塞现象[5-6]。因此，对内镶贴片式滴灌带抗堵塞性能主要影响因素以及堵塞规律的研究对于发展节水灌溉和现代农业具有重要意义。

【研究进展】张新燕等[7]提出贴壁式滴灌带的水源泥沙质量浓度低于100 mg/L 时滴灌带基本不堵塞，大于该值时，滴灌带开始堵塞；张慧[8]研究发现，并非工作压力愈大单翼迷宫式滴灌带的灌水均匀度愈好，而是在压力适中时灌水均匀度愈好；滴灌质量评估和水力设计的核心指标是滴灌带灌水均匀度[9]，其影响因素有主流道内的压力分布，灌水器的制造偏差和堵塞状况，但以压力分布为主[10]；滴灌系统毛管底部泥沙淤积主要受到泥沙颗粒粒径、密度、堵塞滴头数量等因素影响[11]；Wang 等[12]通过对含沙水灌溉下迷宫式灌水器的物理堵塞特性试验发现，堵塞特性与灌水器类型、泥沙量、泥沙粒径有关；罗春艳[13]通过室内堵塞试验，研究了压力、堵塞率、堵塞位置等对滴灌系统灌水均匀度影响规律，Bounoua[14]研究发现，颗粒物粒径是导致物理堵塞的重要原因，通常颗粒物粒径越大、质量浓度越高，堵塞情况越严重；赵青青[15]研究表明，铺设长度对低压供水模式下灌水均匀度的影响最显著；何建新等[16]在研究沥青胶浆拉伸强度变化规律中运用极差分析和投影寻踪回归（PPR）对填料类型、填料浓度和试验温度的三水平正交拉伸试验结果进行分析预测得到较好的效果。在多目标优化算法中，多目标遗传算法（NSGA-II）得到了较多的应用[17]；通常情况下，多目标优化问题中多个目标间具有冲突关系且没有绝对最优解而只有Pareto 最优解，即其目标值向量比其他可行解更好，一类多目标优化求解方法为“预先宣布类”问题[18]，这类方法在解决问题之前，需要给出全部决策者偏好的信息。目前，在研究不同坡度下压力对滴灌带影响的研究中，张天举等[19]研究表明，在毛管上铺设适当顺流下坡坡度或者增加入口压力，都可以改善毛管滴灌均匀度。

【切入点】虽然目前多因素对灌水均匀度和流量降幅影响的研究较多，但是采用多种模型预测各因素对灌水均匀度和流量降幅的影响研究较少。并且多因素对抗堵塞性能影响的主次顺序研究还不够全面。【拟解决的关键问题】为此，本研究设计了三因素三水平均匀正交试验，主要探究铺设坡度、含沙量、工作压力对滴灌带抗堵塞性能的影响，运用极差分析以及层次分析法确定三因素的影响排序，基于线性回归模型、PPR 模型、NSGA-Ⅱ模型对比分析确定最优工况。

1 材料与方法

1.1 材料及设备

试验使用的内镶贴片式滴灌带来自于山东倡民节水灌溉设备有限公司，内镶贴片式滴灌带滴头结构是集正反面流道、中心打孔框和正反流道同一梳型进水口的滴头[20]，其外径为16 mm，滴头间距为30 cm，水力性能参数中流态指数为0.49，流量系数为0.32，额定压力为100 kPa，额定流量为3 L/h。

试验泥沙选用乌鲁木齐西山的自然黄土，将其过120 目筛网。试验在新疆农业大学农业水利工程实验室滴灌带（管道）抗堵塞性能试验台上完成，试验将乌拉泊水库经乌鲁木齐水厂处理后的水作为水源。该设备在10～800 kPa 之间可以随意设置供水压力并精确至2 kPa，压力波动幅度±2 kPa，铺设长度可达35 m。

1.2 试验设计

选用三因素三水平均匀正交表UL9(34)设计试验，试验因素为铺设坡度、灌溉水含沙量、工作压力（分别标记为A、E、B），详见表1。根据前人[19,21-22]研究结果，试验铺设坡度选取-1%～1%；选用的工作压力40～100 kPa。为加快试验进度，扩大预测模型的预测区间，以农田灌溉水质标准[23]为基础，选取灌溉水中悬浮物质量浓度（质量浓度≤0.1 g/L）的10 倍以上，设定浑水含沙量为1、2、3 g/L。

表1 试验设计Table 1 Experimental design

选用3 条长35 m 滴灌带，架设于抗堵塞测试平台（重复2 次，取其均值），调试铺设坡度，每条滴灌带等距选取滴头25 个，将集水桶（1 000 mL）置于其下集水；浑水开始前，在清洗干净的浑水罐中加入清水，然后在计算机终端设定测试压力值，测出当前条件下的清水流量；清水试验结束后，保持原有布置不变，在浑水罐中加入配置好的相应质量浓度的含沙水，再设置计算机终端上的测试压力值40、70、100 kPa，灌水时间30 min，间隔时间30 min，然后进行一次性浑水灌水，待灌水结束后进行10 min 的流量测量。

1.3 灌水均匀度和流量降幅评价指标

采用克里斯琴森均匀系数[24]表示灌水均匀度。计算式为：

式中：Cu为灌水均匀度；¯为每个滴头的平均流量（L/h）；qi为各滴头流量（L/h）；N为试验的滴头数。

目前对于滴灌带抗堵塞性能的评价尚无统一标准，该试验以克里斯琴森均匀系数即灌水均匀度Cu和流量降幅qd来评价滴灌带物理堵塞性能。

式中：qr为平均相对流量（%）；qd为流量降幅；为浑水条件下的平均流量（L/h）；¯为清水条件下的平均流量（L/h）。

1.4 层次分析法

利用AHP 模型[25]对无交互作用的正交试验数据进行统计分析，给定的正交试验因素水平见表2（其中k个因素为E(1)、E(2),…,E(k)，每个因素的水平数分别是m1、m2,…,mk），第j水平下的试验数据之和为Kij，称为试验的影响效应，若试验指标越大越好，则令Mij=Ki；否则令Mij=1/Kij，由此组成试验影响效应矩阵见式（4）。

表2 因素水平表Table 2 Factor levels table

将试验影响效应矩阵按式（5）将每列进行归一化后再按式（6）进行计算后得到右乘矩阵S。2 个矩阵相乘可得到水平标准影响效应矩阵ES。

Ri（i=1, 2,…,m）是第i个因素的极差，将Ri按式（7）进行计算可得影响权重矩阵。

最终将上述的水平标准影响效应矩阵与影响权重矩阵进行计算得到各因素水平对指标的影响权重大小为ω，如式（8）所示：

式中：ω为（m1+m2+…+mk）×1 向量。

1.5 模型介绍及模型误差的判别

用SPSS 23.0 通过最小二乘法进行回归分析时，需要考虑因素水平间的显著性差异，其中规定P＜0.05则表现为显著，P＜0.01 则表现为极显著[15]。为进一步评估模型表现效果，采用了模型评估指标：标准均方根误差nRMSE[26]。

现有回归分析都以正态假定为前提，然而多数检验结果其实并不完全为正态。PPR 模型具有不需要对其数据分布类型进行假设以及以正态假设为前提等优势[27]。利用PPR 模型进行无假定建模可以有效解决已有回归分析法存在的局限性，并提高回归方程求解准确性[28]。设x为P维自变量，y为因变量，计算式为：

多目标遗传算法（NSGA-Ⅱ）将多目标优化问题作为研究目标，通过协调各目标函数间的相互关系，进行搜索使各目标函数的取值尽量大（尽量小）、最优解集合为中心而发展起来的演化算法[15]。

2 结果与分析

2.1 均匀正交试验结果

表3 为UL9(34)均匀正交设计与试验结果，根据正交试验结果及式（1）—式（3）计算浑水条件下每个处理的灌水均匀度和流量降幅。由表3 可知，灌水均匀度最大为0.935 1，最小值为0.227 0；流量降幅的最大值为0.501 3，最小值为0.085 1。

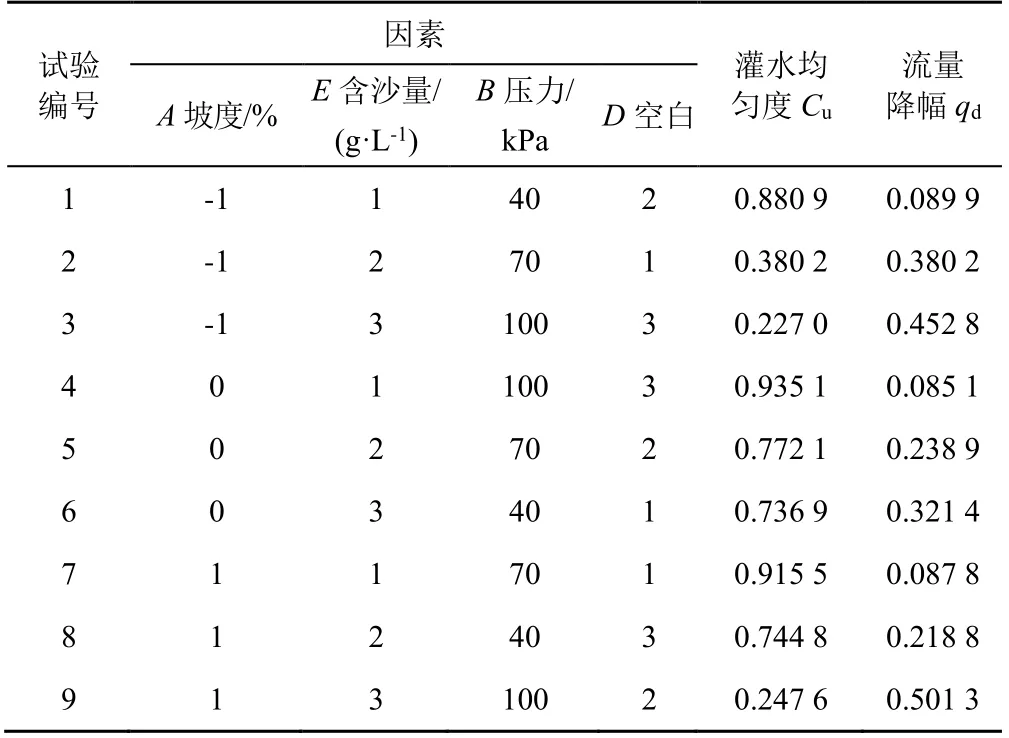
表3 UL9(34)均匀正交设计与试验结果Table 3 UL9 (34) uniform orthogonal design and test results

2.2 影响因素排序

表4 为有关灌水均匀度与流量降幅在不同试验因素下的极差分析。由表4 可知，灌水均匀度极差从小到大排列顺序依次是：RD＜RB＜RA＜RE；按极差从小到大排列滴灌带灌水均匀度各影响因素的顺序是B＜A＜E，即工作压力＜铺设坡度＜含沙量；流量降幅（qd）极差从小到大的顺序依次是RD＜RA＜RB＜RE，按极差大小排列各因素对流量降幅影响顺序依次是铺设坡度＜工作压力＜含沙量。与空白列相比，各试验因素极差都比空白列大，表明各因素间交互作用可忽略不计。

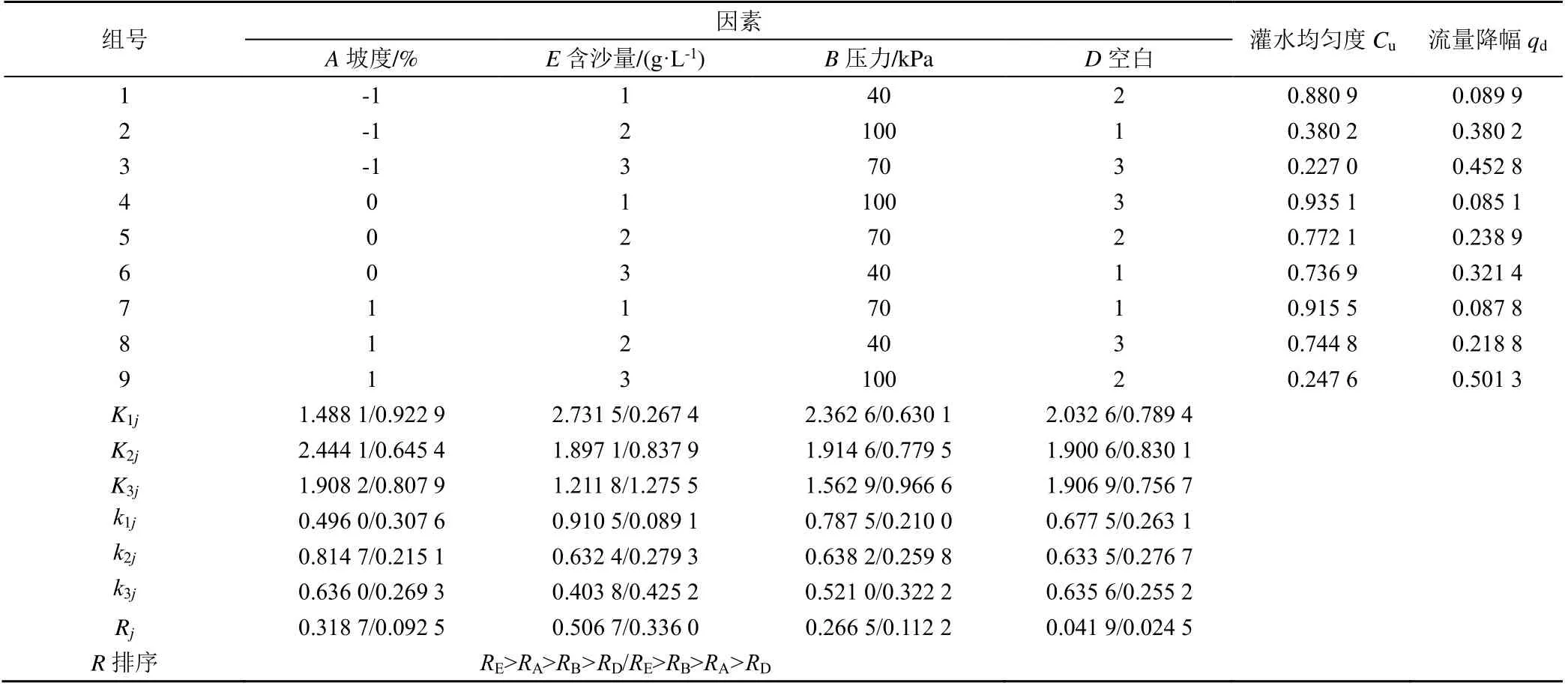
表4 各因素的极差分析结果Table 4 Results of extreme analysis of each factor

不同因素下灌水均匀度和流量降幅见图1。由图1 可知，对于灌水均匀度各因素最优水平取值为：铺设坡度0%，含沙量1 g/L，工作压力40 kPa；对于流量降幅各因素最优水平取值为：铺设坡度0%，含沙量1 g/L，工作压力40 kPa。由于极差分析法存在一定的局限性，对于由试验误差引起的还是由各因素变化所引起的误差难以分辨，因此，须进行层次分析来弥补极差分析的不足。

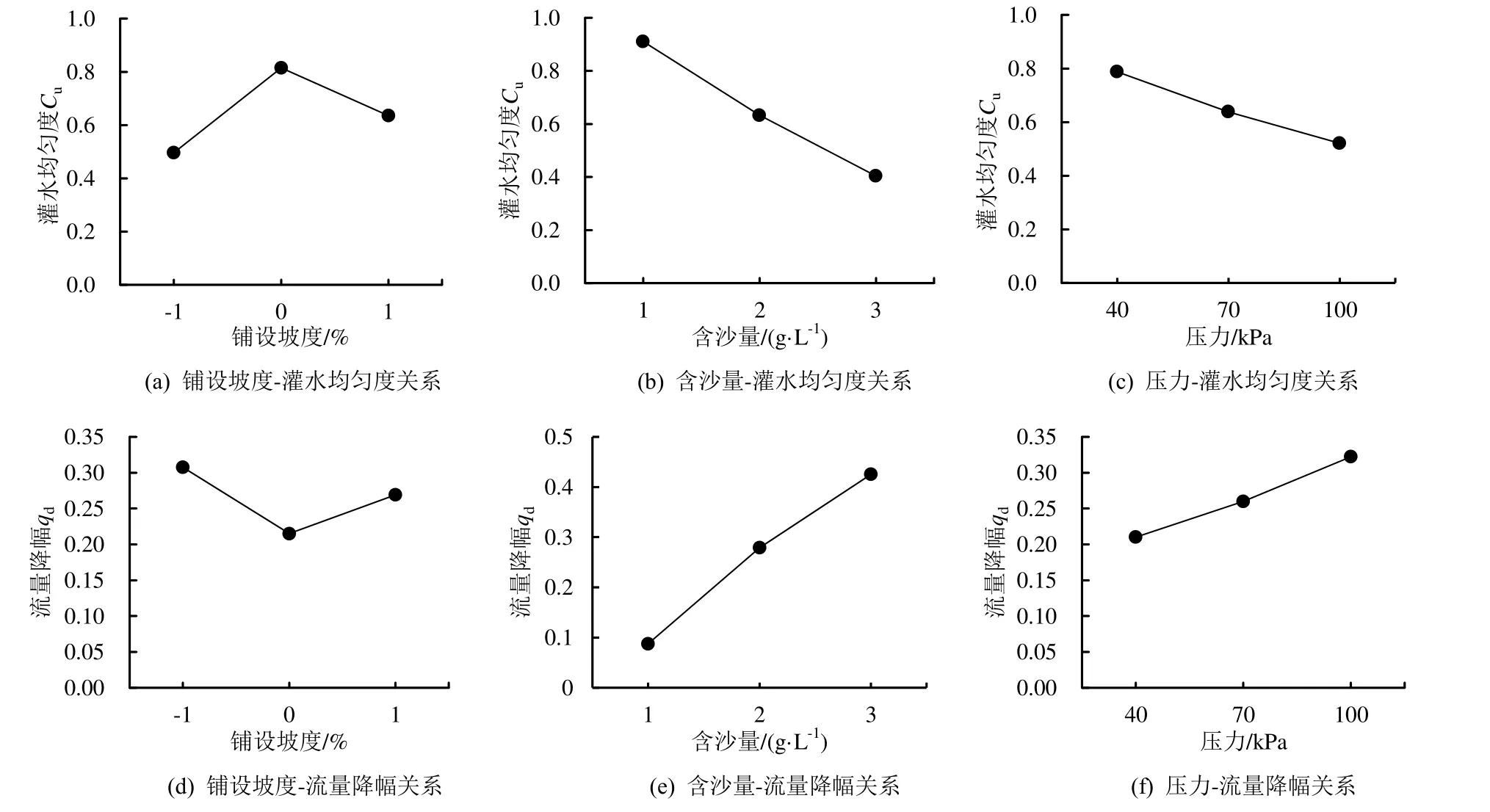
图1 不同因素下灌水均匀度和流量降幅Fig.1 Irrigation uniformity and flow rate reduction under different factors

由表4 及式（4）—式（8）可得，各因素水平对试验指标影响程度大小如式（10）所示。因素A（铺设坡度）三水平对指标的影响权重最大的是A1=0.171 8（灌水均匀度）、A2=0.068 4（流量降幅），因素E（含沙量）三水平中影响权重最大的是E3=0.222 9（灌水均匀度）、E1=0.406 5（流量降幅），因素B（工作压力）三水平中权重最大的是B3=0.041 5（灌水均匀度）、B1=0.084 4（流量降幅）。故试验因素的最优值为A1E3B3（灌水均匀度）、A2E1B1（流量降幅）。各因素主次排序根据因素A、E、B各级影响权重大小来确定，可以得出灌水均匀度主次排序依次是：含沙量＞铺设坡度＞工作压力。流量降幅的主次顺序为：含沙量＞工作压力＞铺设坡度，层次分析结果与极差分析结果一致。

式中：ω1表示各因素对灌水均匀度的影响权重；ω2表示各因素对流量降幅的影响权重。

2.3 线性回归模型

线性回归分析表明，各因子共线性诊断VIF值在5 以下，符合线性回归分析。通过计算得到各影响因子之间的相关系数及回归系数，构建基于最小二乘SVM 法的预测模型。结果表明，此模型有良好的预测能力。以铺设坡度A、含沙量E、工作压力B为试验因素，灌水均匀度Cu、流量降幅qd为考核指标，在95%置信度下采用多元线性回归分析。

灌水均匀度（Cu）的线性回归模型如式（11）所示，对线性回归模型进行试验验证，由表5、表6 可知，不同处理间灌水均匀度有显著差异；各因素之间也有显著相关性；该模型调整后决定系数R2=0.682。建立的灌水均匀度（Cu）模型中，铺设坡度（A）和压力（B）的显著性值（P值）均高于0.05，而含沙量（E）的P=0.012＜0.05，说明可能存在未考虑因子或非线性关系[29]。因此还需采用非线性方法对灌水均匀度（Cu）与各影响因素进行拟合。

表5 灌水均匀度回归方差分析表Table 5 Anova with regression of irrigation homogeneity

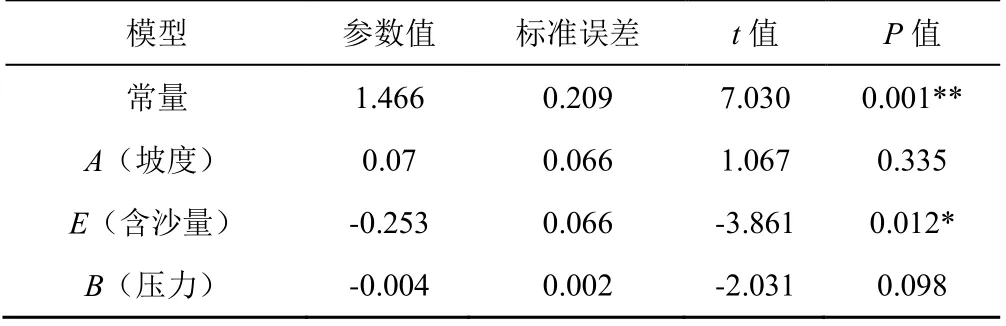
表6 灌水均匀度回归参数估计和检验Table 6 Estimation and test of irrigation homogeneity regression parameters

灌水均匀度线性回归模型：

式（12）为流量降幅（qd）线性回归模型，模型分析表明，当其他因素不变，铺设坡度由平坡向正坡或者负坡变化过程中，流量降幅均呈增大趋势，铺设坡度接近平坡时流量降幅变小。

流量降幅回归方差分析及各项回归参数的估计与检验结果见表7、表8。由表7、表8 可知，调整后决定系数R2为0.900，回归方程拟合效果较好，说明流量降幅（qd）变化时，多数可由铺设坡度（A）、含沙量（E）、工作压力（B）所解释。含沙量（E）的P＜0.01，而工作压力（B）的P值为0.042，铺设坡度（E）的P值为0.396，因此含沙量的回归系数在0.01 水平下显著，工作压力的回归系数在0.05 水平下显著，而铺设坡度对于流量降幅无显著影响。

表7 流量降幅回归方差分析表Table 7 Analysis of variance of flow reduction regression

表8 流量降幅回归参数估计和检验Table 8 Flow drop regression parameter estimation and testing

残差分析发现，建立的模型残差符合正态分布。由上述结果可知，采用该线性回归模型探究含沙量、铺设坡度、工作压力对流量降幅的影响关系是恰当的。

模型输出如下：

灌水均匀度预测模型的绝对误差在±0.189 9 以内，最大相对误差为57.27%，nRMSE=19.15%＜20%；流量降幅的绝对误差在±0.079 9 以内，最大相对误差为93.89%，nRMSE=14.81%＜20%。由此可以看出，以上2 个模型虽表现效果良好，但存在某些预测结果误差较大的问题，故尝试使用非线性回归分析解决相关问题。

2.4 投影寻踪回归模型

用PPR 对灌水均匀度进行计算分析，实测值与预测值的误差如表9 所示。由表9 得知，灌水均匀度（Cu）绝对误差为±0.022 4，灌水均匀度（Cu）非线性模型的nRMSE=2.98%＜10%，相对误差小于9.07%；流量降幅（qd）的绝对误差在±0.012 7 以内，流量降幅非线性模型的nRMSE=2.42%＜10%，相对误差小于5.31%；以上2 个考核指标建模样本数据相对误差均在10%以内，其合格率均为100%且2 个模型的标准均方根误差均小于10%，模型表现效果极好。

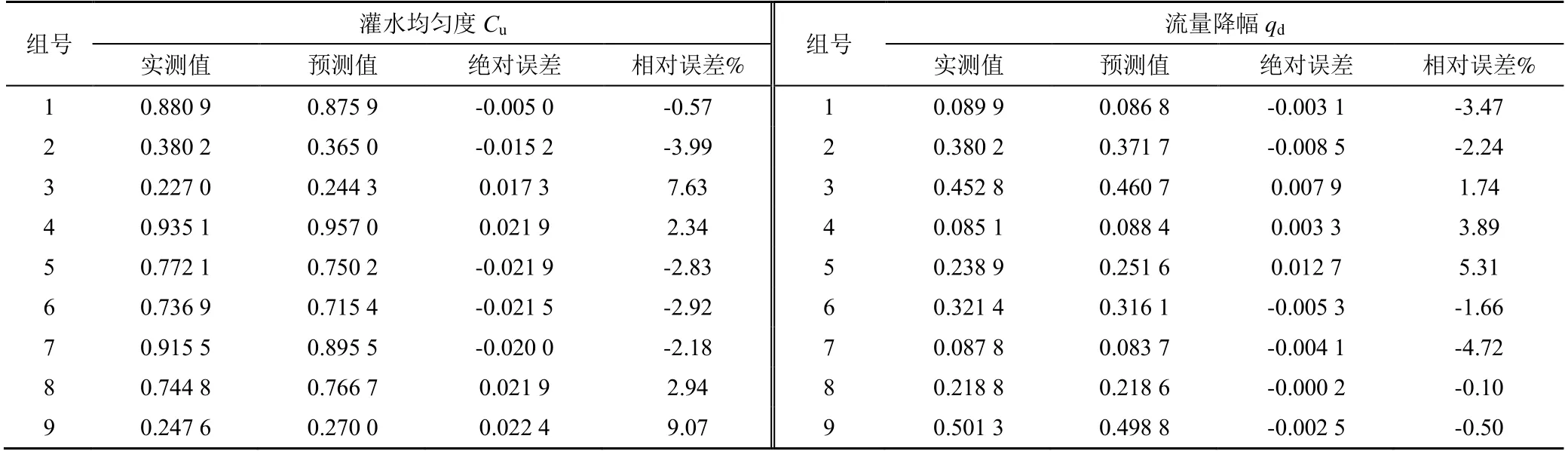
表9 PPR 模型计算结果Table 9 Results of the PPR model calculations

对所得到的最优工况组合进行优化仿真模拟计算，当铺设坡度为0%，含沙量为1 g/L，工作压力为40 kPa 时，流量降幅的最小值为0.041 1，此工况下灌水均匀度为0.831 0；当铺设坡度为0%，含沙量为1 g/L，工作压力为96 kPa 时，灌水均匀度有最大值0.958 5，此工况下流量降幅为0.083 5。

2.5 NSGA-II 模型

基于滴灌带的灌水均匀度和流量降幅与滴灌带的铺设坡度、含沙量、工作压力之间存在非线性关系，使用NSGA-II 进行数学建模，在各因素的约束条件下寻求最优解集。若在某一工况条件下，灌水均匀度与流量降幅的散点落在pareto 前沿附近时，表明此工况为最优工况。由图2 可知，PPR 仿真模拟计算的最大灌水均匀度下流量降幅取值组成的点落在pareto 前沿附近，而另一组PPR 仿真计算结果远离pareto 前沿，表明PPR 模型与NSGA-Ⅱ模型预测结果较为一致，故最优工况为铺设坡度0%、含沙量1 g/L 及工作压力96 kPa，此时灌水均匀度为0.958 5，流量降幅为0.083 5。

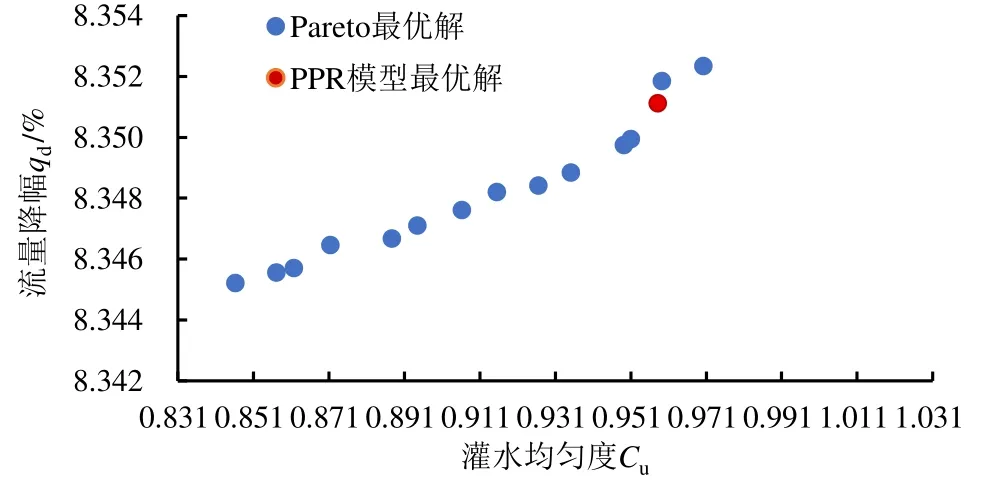
图2 pareto 前沿Fig.2 The pareto frontier

3 讨 论

3.1 不同因素对评价指标影响

本研究表明，含沙量对灌水均匀度和流量降幅影响最大；工作压力对灌水均匀度影响最小；铺设坡度对流量降幅影响最小。这与前人[30-31]研究一致。李治勤等[32]研究发现，含沙量对滴头堵塞影响不显著，只对滴头堵塞之后灌水器堵死进度有影响。这与本试验存在差异，分析其中原因：其试验选取的泥沙粒径主要是大于0.125 mm 的，即使浑水含沙量较小，颗粒依靠重力沉降，也较易堵塞灌水器，而本试验所选泥沙粒径较小（小于0.125 mm），增大含沙量会增加彼此碰撞、黏结的机率，对某些粒径而言，易形成絮团，造成滴头堵塞。浑水滴灌条件下，随着含沙量升高，流量降幅显著升高；较高的工作压力会导致滴灌带堵塞状况越来越严重。

3.2 模型对比分析

本研究表明，建模数据符合非线性分布规律。PPR 建模的方式属于无假定建模，充分利用数据本身有用信息和遵循数据真实规律，利用一系列岭函数之和来逼近回归函数，从而使其具有更高的拟合度。运用SPSS 23.0 方法构建的线性回归模型原理是利用最小二乘法，要求建模数据服从正态分布、方差齐次性等[33]，常需要将数据转换处理成线性方可使用。故建议后续研究中可采用PPR 模型这种无假定建模的方法，可有效处理高维或低维、正态或非正态、线性或非线性、独立或非独立分布的数据。

本研究通过PPR 仿真计算获得以灌水均匀度最大和流量降幅最小的2 组最优解，其Cu均符合《微灌工程技术标准》（GB/T50485—2020）中灌水均匀度大于0.8 的规定，但为了获得唯一最优解，本文采用多目标遗传算法对PPR 仿真计算的2 组最优解进行验证和确定。NSGA-II方法建模得到的是1组pareto最优解集[34]，将PPR 仿真计算结果与NSGA-II 建模的计算综合对比分析，最终确定唯一的最优工况。因此建议后续研究中采用PPR 建模寻求最优工况的同时与NSGA-II 建模的方法相结合，可增强PPR 模型预测结果的可靠性。

由于本研究只考虑了铺设坡度范围-1%～1%，含沙量范围1～3 g/L，工作压力范围40～100 kPa，并未考虑三因素在此范围之外的取值对灌水均匀度和流量降幅的影响，灌水时间、泥沙粒径对滴灌带堵塞的影响本文也未考虑。后续可在探究各因素及水平对内镶贴片式滴灌带抗堵塞性能的影响时进行更加全面的研究。

4 结 论

1）各因素对该滴灌带灌水均匀度影响的排列顺序为：工作压力＜铺设坡度＜含沙量；对流量降幅影响的排列顺序为：铺设坡度＜工作压力＜含沙量。

2）含沙量是影响灌水均匀度和流量降幅的主要因素，影响效果极其显著；工作压力对滴灌带的灌水均匀度和流量降幅的影响效果均为显著；铺设坡度对灌水均匀度影响效果显著，但对流量降幅影响不显著。

3）使用PPR 模型进行优化仿真计算得到该滴灌带最优工况为：铺设坡度为0%，含沙量为1 g/L，工作压力为96 kPa；此条件下灌水均匀度为0.958 5，流量降幅为0.083 5。

（作者声明本文无实际或潜在的利益冲突）