导流片对弧度弯管输水性能影响的数值模拟

张晓雷，刘书瑜，郭利霞，吴浩然

（1. 华北水利水电大学水利学院，河南 郑州 450046； 2. 河南水谷创新科技研究院有限公司，河南 郑州 450002）

0 引 言

湍涡结构在自然界中多种多样，迪恩涡流和螺旋流是有压管流中常见的湍涡结构。当水流沿着直管进入弯管时，在弯管的作用下产生离心力，冲击弯管外侧形成对称水流，并沿着弯管管壁流动，最终在弯管内侧中心汇合并继续冲击弯管外侧，从而形成对称的湍涡结构，即迪恩涡［1］。当管内涡线和流线相重合时，管内湍流发生卷吸效应，小尺度涡通过混掺作用形成大尺度涡流，即螺旋流。

迪恩涡流是弯管内固有的湍涡结构，早在20 世纪末，迪恩涡的湍流强度通过多普勒激光流速仪（LDV）测定［2］，但LDV 在测量管壁处湍动能、湍流强度、流速等参数时，有一定局限性［3］。近年来，数值模拟技术伴随着科学技术的发展得到进一步应用。一些学者针对迪恩涡流比选不同湍流模型的模拟精度，修正了湍流动能系数，分析了迪恩涡流的流态分布规律，进一步得出弯管曲率半径对管内压降的影响，相关研究成果成功应用于管路的传热传质［4-8］。此外，螺旋流在管内常常通过不同形式的起旋器形成［9］，李永业等［10，11］、张春晋等［12］分别采用模型试验及数值模拟方法，分析了导叶片式起旋器作用下螺旋流的涡量变化规律，现已成功应用于长距离螺旋流管路输送［13］。

综上所述，迪恩涡流及螺旋流在功能性方面相似，但弯管是导致有压管路振荡的主要因素之一。这是由于水流进入弯管时，管流的拟序结构受到离心力干扰，管内动压分布极其不均，并且迪恩涡流存在较多的小尺度涡流，致使管流能量损失严重［14］，管壁处激励特性不同［15］。因此，本文基于迪恩涡流和螺旋流的水力特性，采用Fluent 模拟弯管在两种湍涡作用下的断面平均流速、动压分布及湍动能分布，重点分析了两种涡流对弧度弯管输水能力的影响。

1 模型建立

1.1 模拟区域

本文根据Enayet 等［2］的物理模型试验，确定模拟区域及管路尺寸参数。模拟弯管管径D选用50 mm，弯管的曲率半径为2.8D，弯管进出口处直管长分别为4.8D和9.6D。由于迪恩涡流是弯管内部固有流态，管内无法直接形成螺旋流，为此，在进口直管内设置环形阵列的导流片用以形成螺旋流。导流片中心距离弯管进口1.5D，导流片长度L=50 mm，模拟区域如图1所示。图1 中:θ*为弯管各断面对应的偏转角度；R为弯管断面的点到弯管曲率中心的距离，导流片以个数N=4 个、高度H=15 mm、偏转角度θ*=60°为例。

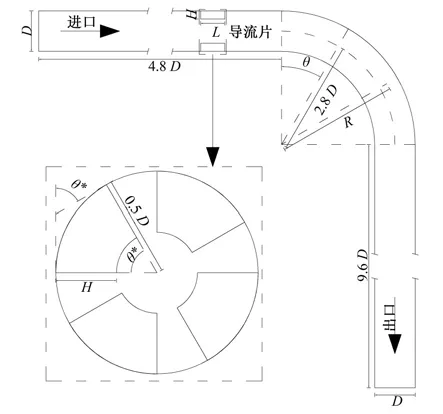
图1 模拟区域及导流片大样Fig.1 Large sample of simulated area and diversion plate

1.2 网格剖分

研究区域采用ICEM CFD 划分结构型网格，为了精确模拟管内涡流运动，网格的立方体尺度应大于含能尺度，且网格计算尺度应小于耗散涡尺度。在大部分壁面湍流的算例中，除了垂直于壁面方向的近壁分辨率外，沿流向及扩散向的分辨率均大于湍流的耗散尺度。为保证数值模拟结果的准确性，模型通过网格的无关性验证最终确定网格整体划分尺度为2.5 mm，局部加密最小网格尺度为0.1 mm。同时，由于导流片厚度较薄，在本次模拟中将导流片视为无厚度的薄片。研究区域的网格剖分见图2，网格整体数量约为65 万，网格质量均大于0.5。

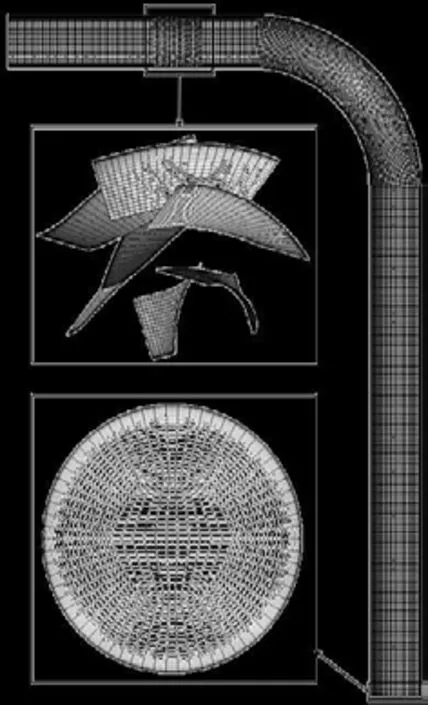
图2 计算区域网格剖分Fig.2 Computational grids in the study domain

1.3 控制方程

湍涡是一种多尺度、多层次结构的流动现象，由于本文研究对象为大尺度涡流，模型计算选用雷诺平均方程（RANS），方程求解通过湍流模型建立一组描写湍流平均量的封闭方程组的理论计算方法。湍流模型结合陈兵等［5］的研究选用Standard k-ε，控制方程如下:

该种湍流模型的速度方程:

式中:t为时间；ρ为密度；k为流体的传热系数；xi，xj表示坐标位置，当i或j为1、2、3 时，分别表示x，y，z三个方向；ui表示xi方向速度；μ表示黏性系数；cp为比热容；Gk表示由层流速度梯度而产生的湍流动能；Gb表示由浮力产生的湍流动能；Ym表示在可压缩湍流中，过渡的扩散产生的波动；C1、C2和C3是常量；δk和δε是方程的湍流普朗特数，Sk和St为自定义常数；Cμ为常量。上述方程的模型常量C1ε、C2ε、C3ε、δk和δε分别取值为1.44、1.92、0.09、1.00和1.30。

1.4 参数设置

模型开边界分别选用速度进口及压力出口，出口相对压强为0 Pa，闭边界选用固壁无滑移条件，壁面粗糙高度根据钢制管件糙率0.012 取值1.0 mm。模型求解器为Coupled，该求解方式可快速地耦合求解加密网格区域的能量及动量方程。所有残差收敛标准均采用10-4，即认为计算值相对误差小于3%时，计算收敛，停止计算。

在统计综合评价中，权重的大小反映了评价指标在整体评价中的相对重要程度。权重越大则该指标的重要程度越高，对整体的影响就越大。反之权重越小则该指标的重要程度越小，对整体的影响越小。对汾河流域节水灌溉发展水平进行评价时，体系中指标的权重直接影响到节水灌溉发展水平评价的准确性和可靠性，因此选择合适的指标权重计算方法至关重要。

2 模型验证及模拟方案

2.1 模型验证

模型进口处流速（V）采用Enayet 等［2］的物理模型0.0102、0.023 及0.92 m/s 三种，以便确保弯管在不同进口流速下两种涡流数值模拟结果的真实性及适用性。图3给出了数值计算结果与实测数据的对比。图中R*=R-2.3D，则R*/D=0、1分别表示为弯管的内侧和外侧，U为断面上某一点的纵向流速，UAve为该断面的平均流速。

图3 横断面上纵向时均速度分布Fig.3 Longitudinal mean velocity distribution in cross section

由图3可知:管流在小雷诺数的条件下，管壁处雷诺剪切应力由于黏性项差异导致平均剪切应力控制方程输出结果相对较小，且平均剪切应力控制方程的计算结果误差随着管流雷诺数的增大而减小，从而导致模拟结果在30°截面管壁处误差偏大。当V=0.010 2 m/s 时，数值模拟结果误差分别在弯管内外侧分别在0＜R*/D＜0.13、0.84＜R*/D＜1 均大于10%；当V=0.023 m/s时，数值模拟结果误差仅弯管外侧0.89＜R*/D＜1 大于10%。管流在大雷诺数的条件下，涡量场中涡管微段表现为“细长”，相邻间距较大，涡流强度较高，涡线拉伸剧烈，涡流变形速率张量的计算结果偏差随着流速降低而减小，从而导致模型进口流速V=0.92 m/s 时，60°截面弯管内侧的误差偏大，模拟结果误差仅在弯管内侧0.20＜R*/D＜0.27 大于10%，此后模拟值与实测值基本吻合。总体来看，该模型能够较好地模拟弯管内多尺度涡流的湍流特性。

2.2 模拟方案

本文共设计了140 种工况，通过数值模拟系统地分析两种涡流对弯管输水能力的影响。模型进口流速区间根据《建筑给水排水设计规范》（GB50015-2019）对应管径50 mm的最大设计流速1.50 m/s 进行区间取值，模型进口流速V选用0.50、0.75、1.00、1.25及1.50 m/s。此外，为了形成不同强度的螺旋流，对导流片个数N、高度H、偏转角度θ*均设置了3种变量值，导流片组合具体见表1。

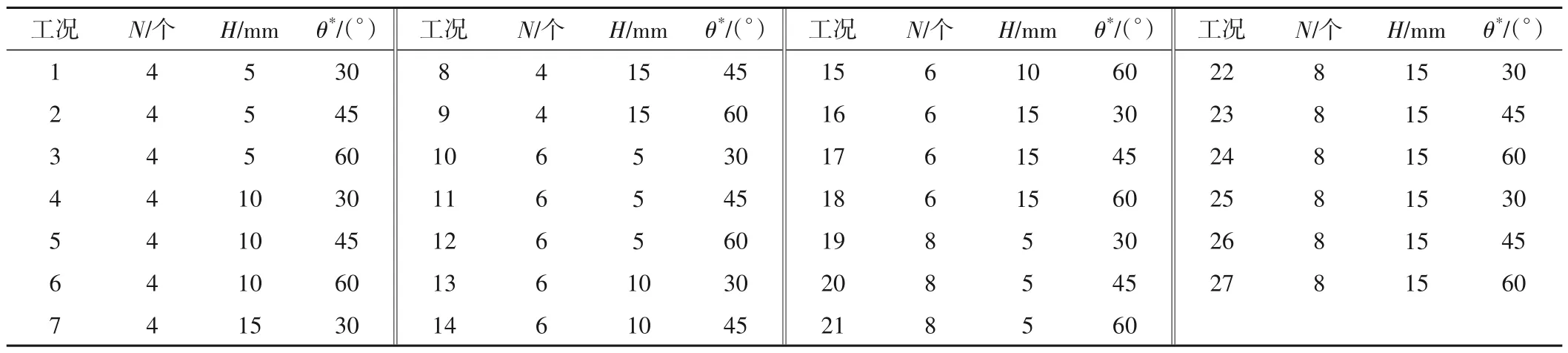
表1 导流片组合Tab.1 Guide plate assembly

3 模拟结果及分析

3.1 管内断面平均流速分析

由于弯管内存在湍涡结构，管流有效过水断面呈三维曲面，且湍涡结构进入下游直管后需经过一定长度才能消除，因此通过对比管流不同断面平均流速大小来确定两种涡流的输水效率。图4 给出了模型中典型断面平均流速（UAve）在140 种工况下的分布，图4 中将导流片组合按照导流片高度分为3 类，将管内未架设导流片的组合视为空白组，后文中的空白组均代表弯管内迪恩涡流的工况。

图4 不同工况下模型典型断面平均流速分布Fig.4 Average velocity distribution of typical sections under different working conditions

由图4 可知:不同导流片组合形成的螺旋流可提升或降低弯管的输水效率，管流在各横断面中，弯管输水效率随着导流片高度H和进口流速V的增大而增大，相同导流片高度的输水效率随着管流流速的增大而分化明显。当V=1.5 m/s时，空白组和导流片组合27在弯管进口断面处的平均流速分别为1.246和1.511 m/s，此时螺旋流对弯管的输水效率提升至最大值10.62%；当V=0.5 m/s 时，空白组和导流片组合19 在模型出口处的平均流速分别为0.452 和0.401 m/s，此时螺旋流对弯管的输水效率削弱至最大值11.79%。

为研究螺旋流削弱、提升弯管输水效率的成因，图5给出了V=1.5 m/s 的条件下，导流片组合工况1、3、7、9、19、27 的断面平均流速沿程分布。分析可知:当螺旋流提升管流的输水效率时，导流片组合7、9、27作用下的管流输水效率沿管流方向逐渐降低，导流片组合27 在弯管进口断面附近达到了1.511 m/s；当螺旋流削弱管流的输水效率时，导流片组合1、3、19作用下的管流输水效率呈先增大、后降低的变化趋势，导流片组合1在弯管出口后20 mm 的断面平均流速达到最大值1.337 m/s，对弯管输水效率的削弱达到最小值2.95%。

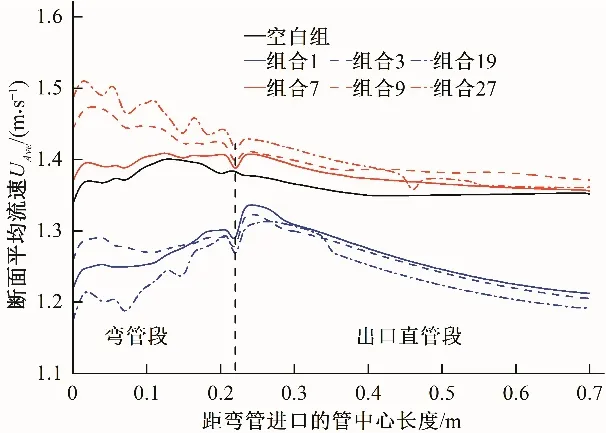
图5 管内涡流输水效率Fig.5 Water transfer efficiency of vortex in tube

结合图4 和图5 可知:①当螺旋流强化管流提高输水效率时，相同个数、高度的导流片对弯管输水效率的提升随着导流片偏转角度的增大而增大；相同高度、偏转角度的导流片对弯管输水效率的提升随着导流片的个数增加而增大。②当螺旋流削弱管流降低输水效率时，相同个数、高度的导流片对弯管输水效率的削弱随着导流片偏转角度的减小而增强；相同偏转角度、高度的导流片对弯管输水效率的削弱随着导流片个数的增加而增强。③当导流片高度达到15 mm 时，该种导流片组合下产生的螺旋流对弯管的输水效率具有提升作用。

3.2 管内动水压强分析

由于管件在动载、低温等条件下极易发生断裂，管路的设计压力常依据管内工作压力确定。因此，为了研究两种涡流安全稳定的输水性能，图6 给出了两种涡流在管内的动水压强分布。

当进口直管未架设导流片时，管内动压分布具有明显的横向梯度，平均动压为956 Pa、最大动压为1 619 Pa，管流中高压区域主要集中在弯管内侧及出口直管左侧，弯管出口处管路两侧压差较大，并且管流在迪恩涡影响下，出口直管内动压梯度分布持续至模型出口；当进口直管架设导流片时，导流片组合19的动压分布与迪恩涡主导下的管流动压分布基本相同，整体动压峰值相对较小，导流片组合27 在弯管内动压分布相对均匀，管路整体平均动压为1 168 Pa，最高动压为2 270 Pa，高压区域主要集中在进口直管末尾段、弯管及出口直管进口段。

管流动压的分布不均对管路系统存在着潜在风险。为此，通过量纲分析定义管内某一点处致使管道发生事故的风险率Hr（Hazard rate）为:

式中:d为该点距管轴线距离；P'为该点的动压；PAve为管内平均动压。若管内某点处的事故风险率Hr＞100%，则表明该点处的风险率较高，该点所处的区域为高危风险区域。管内横断面处的风险率分布如图7所示。

图7 管内风险率分布Fig.7 Distribution of hazard rate in tube

结合图6 和图7 可知:①空白组的整体最大事故风险率为149.64%，出口直管左侧为主要风险区域，平均事故风险率为114.82%，且该风险区域持续至模型出口；②管路系统在导流片组合19 导流下的整体最大事故风险率为158.50%，出口直管左侧仍为主要风险区域，平均事故风险率为115.94%；③管路系统在导流片组合27 导流下的整体最大事故风险率为125.23%，相对前两种工况较小，主要风险区域集中在弯管内侧，平均事故风险率为107.37%。

3.3 湍涡结构分析

由前文可知，导流片组合19 和导流片组合27 分别削弱、提升了弯管的输水效率及管路的安全稳定性。为研究该种现象产生的原因，图8 给出了当V=1.5 m/s 时，管内湍动能及断面流线分布，其中断面1、断面4 分别位于弯管进、出口，断面2、断面3 及断面5、断面6 分别将弯管和出口直管均分三等份，断面视图均为从下游至上游。

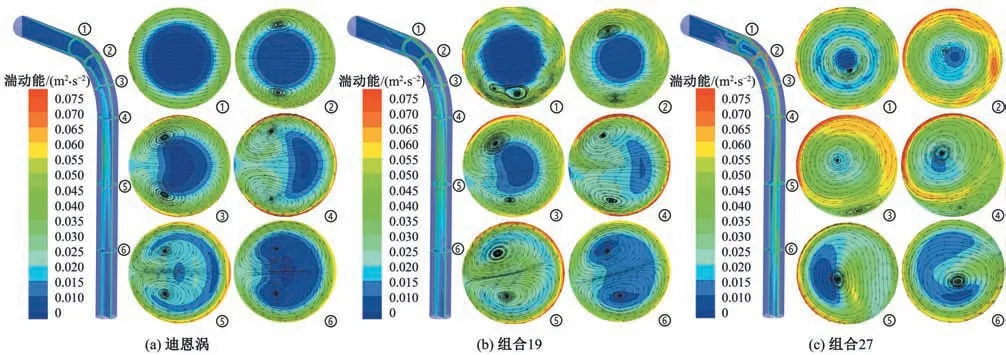
图8 湍动能及流线分布Fig.8 Turbulent kinetic energy and streamline distribution

当管内某一横断面流线涡核发生偏移时，管内流线涡核预示着下一个断面处的湍动能增大，结合Kolmogorov 的各项同异性假定可知，当管内某断面处湍动能相对上一个断面流线涡核处的湍动能增加时，管内大尺度涡流耗散作用相对较弱，涡流之间相互诱导、卷吸，湍涡结构衰弱相对缓慢，并且涡流在边界条件的作用下发生拉伸变形，表征为各项异性；当管内某断面处的流线涡核不再发生偏移时，管内涡流进入缓慢耗散期，小尺度涡流结构在统计上与时均运动、大尺度涡流无关，表征为各项同性，且湍流的涡能在这一层级的涡流逐渐耗散。

流体脉动对管壁壁面的激励特性具体表现为管壁结构上的振动响应，且管路系统的振动频率常与管内涡流脱落频率有着较高的重合度。而湍流强度I表征脉动流速的均方根与平均流速的比值，在Standard k-ε湍流模型中，湍流强度I与湍动能k及断面平均流速UAve存在如下关系:

结合图5 和图8 可知，当管内未架设导流片时，管内各断面平均流速在弯管60°截面达到最大，而管内湍动能在弯管出口截面上达到最大值0.035 m2/s2，各断面右端的湍动能在断面4～5 增大，断面5～6 减小，则断面5 右端的湍流强度较大，最大湍流强度为0.214 1，属于高湍流强度，表明管路输水发生事故的风险率较高。

当弯管进口以低强度的螺旋流进入弯管时，管内湍动能、流速变化趋势与管内未架设导流片的工况相一致，管内湍动能也基本相同。然而，管内壁处的湍动能在横断面3～5 相对较大，管内断面平均流速相对较小，平均流速最大值所处的断面相对滞后。由此可得低强度的螺旋流致使管内湍流强度相对较大，从而扩大了管内事故高危风险区域。

当弯管进口以高强度的螺旋流进入弯管时，管内各横断面平均流速变化趋势呈持续减小，并且湍动能在弯管出口截面上达到最大值0.044 m2/s2，则弯管出口断面附近的湍流强度较大。由于出口断面较大的湍动能集中在弯管内侧，则弯管内侧的湍流强度局部较大，最大湍流强度为0.237 7，对管路系统地安全运行存在着潜在的风险。

4 结 论

本文基于Fluent 建立了三维数学模型，并利用前人物理模型试验数据进行了验证，最后基于验证后的模型模拟了弯管内不同尺度、不同强度的湍涡结构，重点分析了曲率半径为2.8D的弯管管路系统在不同涡流导流下的输水效率及安全稳定性能。主要得到以下结论:

（1）管路系统进口流速V=1.5 m/s 时，弯管内迪恩涡流不仅削弱了管路系统的输水效率，还导致下游管路长达9.6D以上的流态恶化，且湍流强度在出口直管局部达到21.41%，对管路系统的输水安全稳定性产生巨大威胁。

（2）管路系统进口流速V=1.5 m/s 时，在导流片工况27 的作用下，弯管进口处的湍动能总体提升34.42%，管内涡流个数从单一的螺旋流分化形成两个不同尺度涡流，最终在管壁的作用下形成单一的大尺度涡流，不仅使弯管的输水效率提升10.62%，还提高了管路系统的输水安全性能。

（3）通过对管内湍涡结构的分析，利用湍流特性进一步验证了管路基于量纲分析的风险评估，可为水利工程的设计及应用提供技术指导。