基于防洪重现期的水库安全设计研究
陶昌弟,刘 旻
(1. 广西壮族自治区水利电力勘测设计研究院有限责任公司,广西 南宁 530027;2. 广西珠委南宁勘测设计院有限公司,广西 南宁 530027)
0 引 言
水库防洪安全设计作为一种主要的水文事件,是当前多变量水文事件中研究的热点。然而,现阶段水库的防洪安全设计,大多以单一变量来控制,忽略了变量间的相关性,无法全面反映洪水事件的真实特性[1]。多变量水文分析计算则考虑了各水文要素的相互关系,能更好地描述水文事件的内在规律,其计算分析的关键在于变量间联合分布的构建、多变量重现期的定义以及设计组合的选取3 个方面[2]。水库防洪安全设计中,有关联合分布构建以及设计组合选取的问题已有大量研究,但研究过程中并未过多地考虑设计重现期对设计结果的影响,不同的重现期标准下对应的水库设计值应有所区别。
当前基于联合分布的多变量重现期,使用最广泛的是联合重现期和同现重现期,它们均根据某一特定的多变量设计组合值定义危险域,当设计组合发生改变时,其对应的危险域判定将会出现矛盾[3,4]。同时,相同重现期水平下不同设计组合计算所得的防洪设计参数也存在较大差异,为工程设计带来不确定性[5,6]。由此,Salvadori 等根据联合重现期、同现重现期的不足,相应地提出了两种新的多变量重现期定义,即Kendall 重现期与生存Kendall重现期,以解决不同设计组合对应的危险域不唯一的问题[7,8]。
然而就水库防洪安全而言,刘章君等[9]认为应该以坝前最高水位被超过的概率来表示洪水重现期,才能有效的将洪水本身的特性与复杂的调洪规则相结合,并以此定义了结构荷载重现期,对二变量重现期的定义进行了拓宽。显然,水库防洪设计参数的计算除了与遭遇的洪水密切相关外,也与水库的布置型式、泄流方案、调度方式等息息相关。甘富万等[10]认为二变量重现期所反映的不仅是数值上的概率问题,而应该与工程实际紧密联系,并以水利工程正常运行过程中,防洪设计参数f在洪水作用下被超过的平均间隔时间定义防洪重现期,将二变量重现期的定义进行了进一步的拓宽。
因此,为进一步研究防洪重现期在水库防洪安全设计中的应用规律,以柳江上游规划修建的洋溪水利枢纽为研究对象,采用Copula 函数构建洪峰、洪量的联合分布,计算防洪重现期标准下的坝上设计水位,并与4 种常见的二变量重现期对比分析,探讨防洪重现期在水库防洪安全设计中的合理性与可靠性。
1 防洪重现期定义及计算
1.1 联合分布的构建
水库防洪安全设计中,洪峰与洪量是主要的设计变量,我国通常采用皮尔逊Ⅲ型分布作为其边缘分布。对水库而言,洪峰、洪量一般具有较高的正相关性,可采用GH Copula 函数构造峰量联合分布,其计算表达式为[11]:
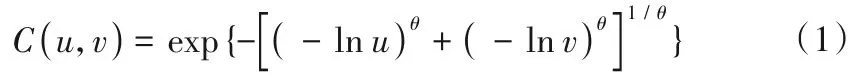
式中:u,v分别为洪峰、洪量的边缘分布;θ为Copula 函数参数,且θ≥1。
1.2 防洪重现期定义
洪水与不同行洪边界的耦合作用下,可产生如闸坝的设计水位、坝顶高程,消力池的跃后水深,渠道的水面线等多种防洪特征参数F。防洪重现期正是为了研究洪水与行洪边界的耦合关系,提出的以水利工程防洪设计参数f在洪水作用下被超过的平均间隔时间来定义的新的多变量重现期[10],表示的是不同的防洪设计参数f这一设计值前后两次被超过的平均时间间隔,其计算公式为:

可知,当洪水相应的防洪参数F大于设计参数f时,水利工程的正常运行将被破坏。研究的防洪设计参数f为洋溪坝址处的设计水位z,该水位受到柳江流域调度规则的影响,与调洪过程密切联系,可使用防洪重现期计算洋溪坝址的设计水位,计算分析防洪重现期在水库防洪设计中的应用规律,此时,相应的防洪重现期计算公式为:
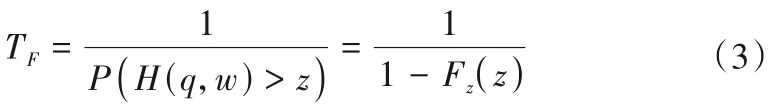
式中:q和w分别表示洪峰和洪量;z为设计水位;Fz(z)为设计水位的累积分布函数。
1.3 基于Copula-Monte Carlo 法的防洪重现期设计水位计算
由防洪重现期的定义可知,防洪重现期的计算转化为了对设计水位z的分布研究。对于峰量组合下的设计水位计算,采用Copula-Monte Carlo 法及条件概率随机模拟n场洪水事件的峰量组合[12],求解设计水位z的分布,步骤如下:
(1)构建的峰量联合分布函数C(u,v),基于条件概率随机模拟n个洪水事件的峰量组合(q,w);
(2)利用二变量放大方法,放大得到该峰量设计组合对应的设计洪水过程线,经调洪模型计算得到n个洪水事件对应的设计水位z1,z2,…,zn;
(3)采用数学期望公式,计算所有坝上设计水位对应的经验频率,得到设计水位累积分布函数Fz(z),不同防洪重现期水平下的设计水位值可通过分布曲线直接查询。
1.4 二变量放大方法
当前针对二变量条件下洪水过程线的处理,同倍比放大法或同频率放大法均存在一定的局限性。由此,肖义等[13]基于二变量重现期下的峰量联合分布,提出了一种可将洪峰、洪量控制在峰量联合设计值的放大洪水过程线的方法,公式为
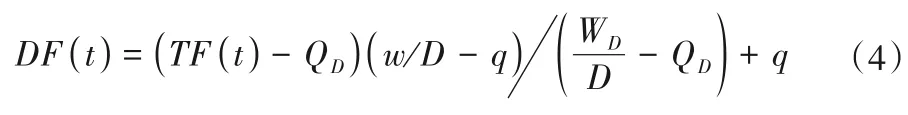
式中:DF(t)和TF(t)分别为洪水历时D内,设计和典型洪水过程在t时刻的流量;QD、WD为典型洪水过程的洪峰、洪量;q、w为设计洪峰、设计洪量。
此方法能将洪峰、洪量控制在随机生成的峰量联合设计值,并保留典型洪水过程线的形状,无需人工修匀。然而,当设计洪量过大而设计洪峰较小时,设计洪水的平均流量会出现大于设计洪峰的情况,洪水过程线的形状倒转,显然不符合水文内在规律;而当设计洪峰过大而设计洪量较小时,设计洪水的平均流量与设计洪峰之间的差值Δq会过大,典型洪水过程在叠加差值后,缩窄了洪水过程,使得设计洪水过程线的形状发生形变,造成调洪结果的不准确。
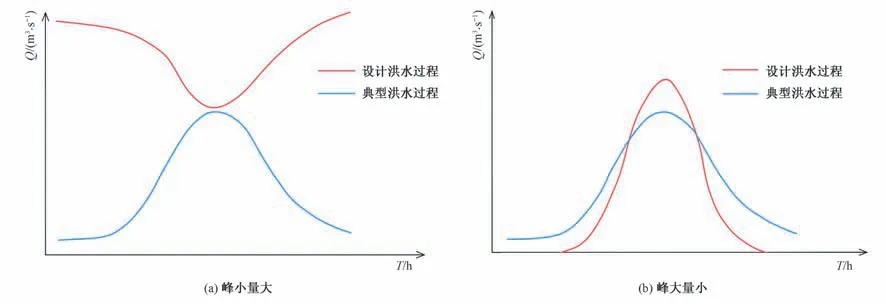
图1 不合理峰量组合下二变量放大方法出错Fig.1 Error of bivariate amplification method under extreme peak volume combination
因此,当基于GH Copula 函数随机模拟出的峰量组合为峰大量小或峰小量大的不合理组合时,洪水过程线放大将会出错,错误的洪水过程线输入到调洪程序后,势必会造成随机模拟结果不准确,给后续的计算分析造成不良影响。为解决此问题,将随机模拟出的峰量组合进行分区处理,处理方法见表1。

表1 随机模拟峰量组合的分区处理方法Tab.1 Zonal processing method of random simulation peak combination
2 五种二变量重现期的对比分析
当前常用的二变量重现期为首次重现期[8]及对应的二次重现期[14],首次重现期包括联合重现期及同现重现期,二次重现期包括Kendall 重现期及生存Kendall 重现期。5 种二变量重现期的危险事件及计算公式见表2,相应危险域的判定标准见表3。

表2 各重现期对应危险事件及计算公式Tab.2 Corresponding dangerous events and calculation formulas for each return period

表3 各重现期危险域划分依据及唯一性Tab.3 Classification basis and uniqueness of risk domains in each recurrence period
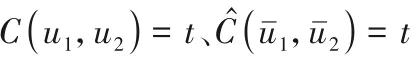
针对洋溪水利枢纽设计水位的计算,防洪重现期则是由设计水位等值线H(x,y) =z作为临界标准划分危险域,等值线上所有组合得到的设计水位一致,各组合抵御洪水威胁的能力也一致,防洪重现期等值线上的所有组合对应的危险域相同且唯一(见图2)。二次重现期仅考虑了洪水自身的特性,而防洪重现期考虑了洪水与工程之间的耦合关系,与工程实际联系密切,更能表征水利工程在洪水及行洪界面共同作用下被破坏的风险。

图2 不同重现期标准对应的危险域Fig.2 Danger zones corresponding to different criteria of return periods
3 工程实例
洋溪水利枢纽位于柳江流域都柳江河段,坝址上游约1.0 km 处设有涌尾水文站。采用1964-2014 年涌尾站连续61 a 实测的水位、流量资料。设涌尾站的洪峰序列样本为变量Q,洪量序列样本为变量W,根据样本数据计算对应的Kendall秩相关系数τ= 0.689 7,再采用Kendall 秩相关系数法计算所得的Copula函数参数θ= 3.222 8,根据式(1),基于GH Copula 函数构建的洋溪水利枢纽的峰、量联合分布模型如图3所示,其相应的计算公式为:
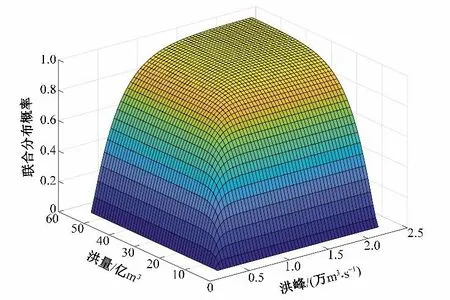
图3 洋溪水利枢纽峰量联合分布模型Fig.3 Joint distribution model of peak

3.1 洋溪水利枢纽设计水位累积分布
洋溪水利枢纽的泄洪建筑物为溢流坝,设泄洪孔10 孔(8低2 高),8 个低孔孔口尺寸为7 m×16 m(宽×高),进口高程为138 m,2 个高孔孔口尺寸为7 m×16 m(宽×高),进口高程为148 m,洋溪汛限水位为153 m,其相应的泄流规模为5 517 m3/s。洋溪调洪方式为:以汛限水位(153 m)作为起调水位,按防洪调度规则蓄泄,水库水位超过防洪高水位时则敞泄,但下泄流量不大于来水。洋溪水利枢纽的防洪高水位,是直接由汛限水位对应的库容,叠加防洪库容后,查水位~库容关系确定的,为186.80 m。
洋溪坝址的洪水过程一般为2~3 d,即使长至7 d 左右,其洪量主要集中在2~3 d内。经比较,最终选择峰高、量大的1996年洪水作为典型洪水过程,并基于已有调度规则,构建调洪模型。根据防洪重现期的计算步骤,随机生成100万组峰量组合。图4 为基于GH Copula 函数随机生成的100 万组变量组合G,表明了洋溪水利枢纽随机模拟组合的分区结果,据统计,排除的α2区中的组合占总模拟数的近0.06%,修正的α3区的组合占总模拟数的近19.5%。处理这两部分峰量组合后,得到的洋溪水利枢纽的设计水位累积概率分布曲线见图5。显然,分布曲线上的每个累积概率值,都对应了一种防洪重现期水平,且每一种防洪重现期水平,都能对应一个确定的设计水位。
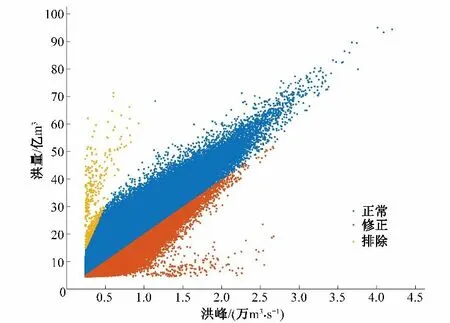
图4 GH Copula模拟的峰量组合散点图Fig.4 Scatter diagram of flood peak-flood volume combination simulated by GH Copula volume of Yangxi Water Control Project
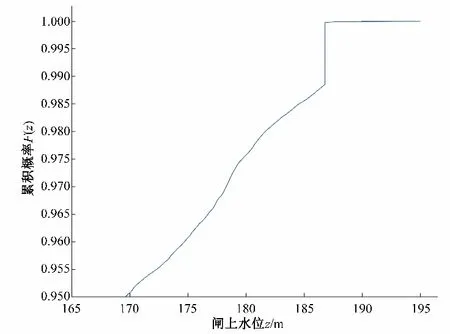
图5 洋溪水利枢纽设计水位累积分布Fig.5 Cumulative distribution of design water level of Yangxi water control project
3.2 考虑洪水与工程耦合的防洪重现期计算分析
由图5查得不同防洪重现期水平下,即TF=50、80、100、200、500 年一遇时所对应的设计水位z,分别为181.63、186.32、186.79、186.79、186.79 m。给定某一洋溪水利枢纽的坝上设计水位z设,满足H(q,w) =z设的所有的峰量组合,都可以满足水利工程防洪标准要求的设计组合。即在洋溪水利枢纽的防洪设计中,不同峰量组合得到的设计水位均相同。因此,防洪重现期计算的设计水位与水利工程的防洪能力一一对应。
图5 中出现一直线段,累积概率不同但对应的设计水位一致,而在累积概率接近1 时设计水位又逐渐增大。这是因为在洋溪水库的调度规则中,当调洪过程中库容蓄水量超过防洪库容时,泄流方式为敞泄,而当发生位于累积概率曲线直线段对应重现期的洪水时,所遭遇的洪峰流量均小于敞泄时的下泄流量,或者在达到敞泄条件前洪峰已经过去,此时洋溪水库库容不再改变,导致设计水位不变;当重现期继续增大时,重现期对应的洪峰流量超出了敞泄时的下泄能力,水库蓄水后库容增大从而使得设计水位继续增高,但变化幅度较小,顶部的累积概率曲线见图6。
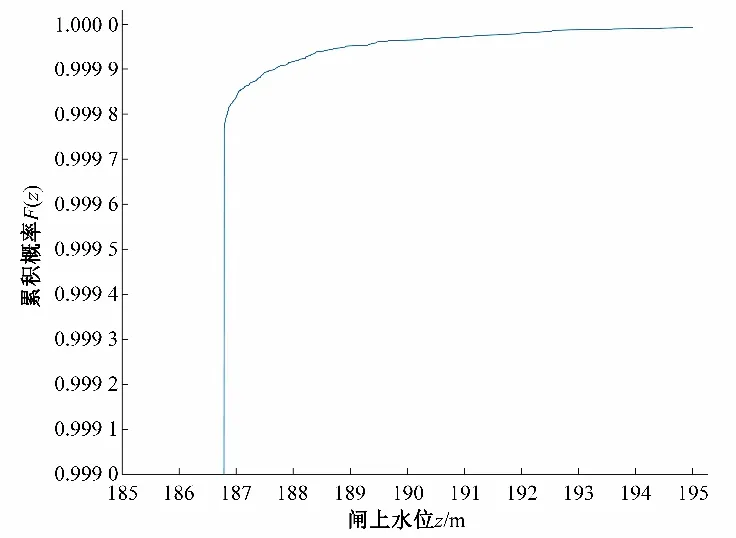
图6 设计水位累积概率曲线顶部放大Fig.6 Enlarged top of cumulative probability curve of design water level
不同重现期水平下防洪重现期的等值线见图7。图7 中分界线为根据随机模拟结果拟合的α1与α2区的分界线,分界线以上的峰量组合均排除在外,不参与调洪。图表明,给定洋溪水利枢纽设计水位,洪峰、洪量呈负相关;在敞泄的影响下,100年一遇、200 年一遇及500 年一遇的防洪重现期等值线相同;当重现期水平由50 年一遇逐渐增大至100 年一遇时,防洪重现期等值线上、下尾部的斜率,较中部区别更为明显,其等值线中部总体斜率绝对值越接近1,说明从小重现期到大重现期,防洪重现期等值线上、下尾部的峰量组合对洪水的控制作用趋近于单变量控制,而等值线中部的峰量组合,更趋近于洪峰、洪量共同对洪水起控制作用。
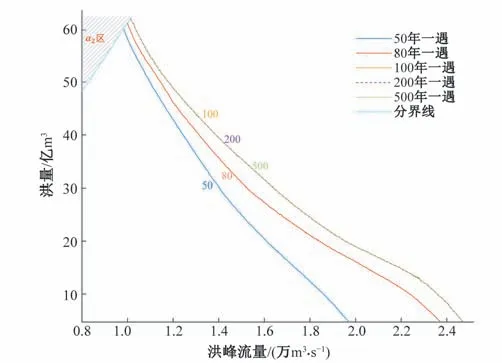
图7 不同防洪重现期水平对应的等值线Fig.7 Isolines corresponding to different flood control return period levels
洋溪水利枢纽的设计水位取决于调洪模型,其蓄泄能力与各方案下的泄流能力有关,可计算分析不同泄流方案(9 孔、10孔、11孔)下防洪重现期等值线的变化规律。相同重现期水平,不同泄流方案下的防洪重现期等值线图见图8。图8 表明,当汛限水位一定时(153 m),改变泄流方案,防洪重现期对应的计算结果发生明显改变,且防洪重现期等值线的下尾部斜率变化较为明显,形状总体上呈现从下凹到趋直的趋势,说明其调洪作用逐渐趋向于洪峰、洪量共同控制,各泄流方案下防洪重现期所对应的设计水位见表4。
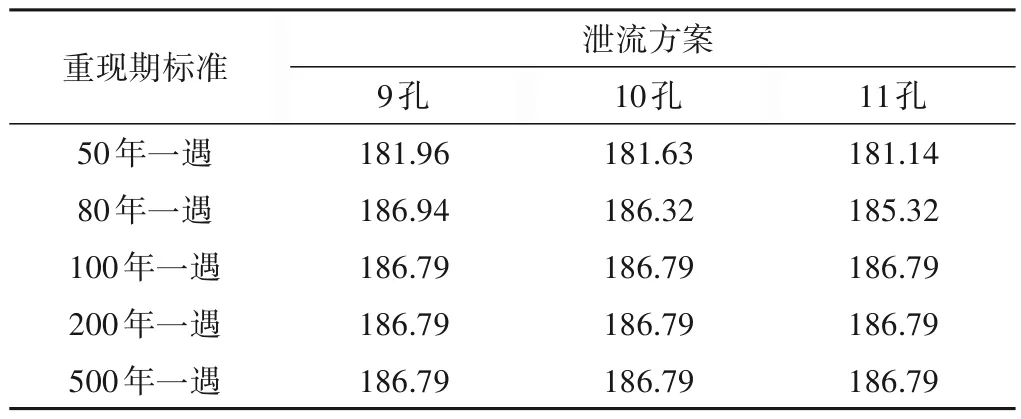
表4 不同泄流方案下防洪重现期设计水位计算结果(汛限水位153 m) mTab. 4 Calculation results of design water level in flood control return period under different discharge schemes (flood limit water level 153 m)
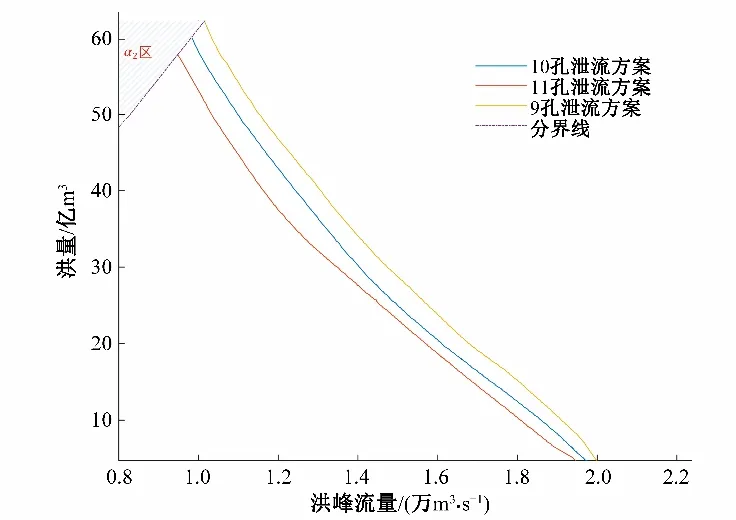
图8 50年一遇防洪重现期等值线Fig.8 Contour of return period of flood control with 50 years return period
同时,100、200 及500 年一遇时,各泄流方案下防洪重现期计算的设计水位一致,说明当发生以上对应的洪水时,各泄流方案虽然泄洪孔数不一致,但其敞泄时的下泄能力依然能满足防洪库容的要求。
综上可知,防洪重现期等值线的形状与泄流方案有关,即与泄洪建筑物所涉及的水力要素相关联,防洪重现期与行洪边界存在耦合关系,更符合工程实际情况。
3.3 5种二变量重现期的设计水位计算分析
根据表4,绘制出不同重现期水平下(50,100,200,500 年)的传统二变量重现期等值线,并与防洪重现期等值线进行对比。如图9 所示,联合重现期与Kendall 重现期,同现重现期与生存Kendall重现期的等值线相似。然而,对于同一峰量组合来说,其对应的Kendall 重现期水平大于对应的联合重现期水平,对应的生存Kendall 重现期水平小于对应的同现重现期水平。防洪重现期等值线的形状与这四种常见的二变量重现期等值线的形状有较大差异。
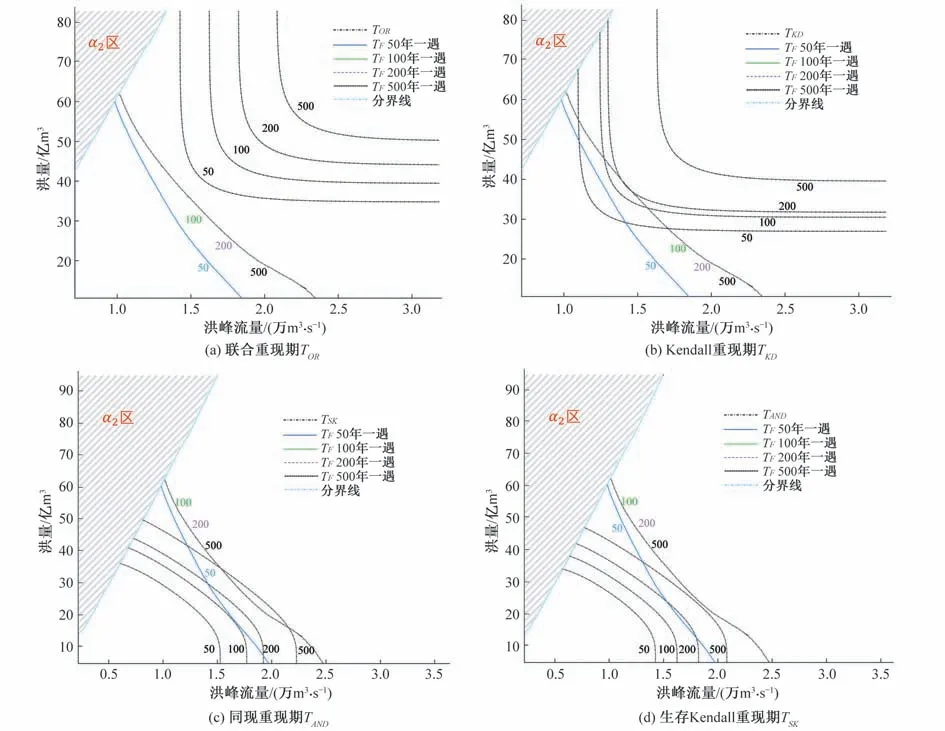
图9 防洪重现期与传统重现期的等值线对比Fig.9 Isoline comparison between flood control return period and traditional return period
5 种二变量重现期在不同重现期标准下,相同重现期水平的等值线见图10。图10 中,垂直、水平渐近线分别为单变量控制下洪峰、洪量相应的单变量设计值。图10表明,联合重现期、Kendall 重现期位于防洪重现期上方,同现重现期、生存Kendall重现期位于防洪重现期下方,但首次重现期与防洪重现期均未交叉,而二次重现期与防洪重现期存在交叉,也说明在水库的防洪设计中,Kendall 重现期、生存Kendall 重现期等值线上,存在与洪水威胁相适应的设计峰量组合,相比联合重现期、同现重现期更为合理。
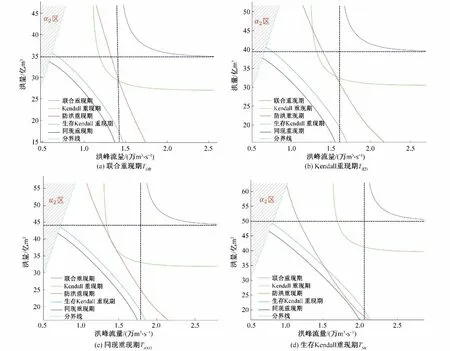
图10 相同重现期水平不同重现期标准对比图Fig.10 Comparison diagram of different return period standards at the same return period level
5 种二变量重现期对应的峰量同频设计值组合见表5。表5 给出了洋溪水利枢纽达到敞泄条件时的下泄流量,显然敞泄时的下泄能力远超出了100、200 及500 年一遇洪水时的设计洪峰,调洪过程中水库库容可维持在防洪库容,因此计算所得的设计水位相同。根据同频设计组合,分别计算不同重现期标准下对应的洋溪水利枢纽设计水位,结果见表6。再将各重现期标准下的设计水位,根据洋溪水利枢纽的设计水位累积分布曲线,反推累积概率,可得到不同首次重现期与二次重现期水平所对应的防洪重现期水平,结果见表6。
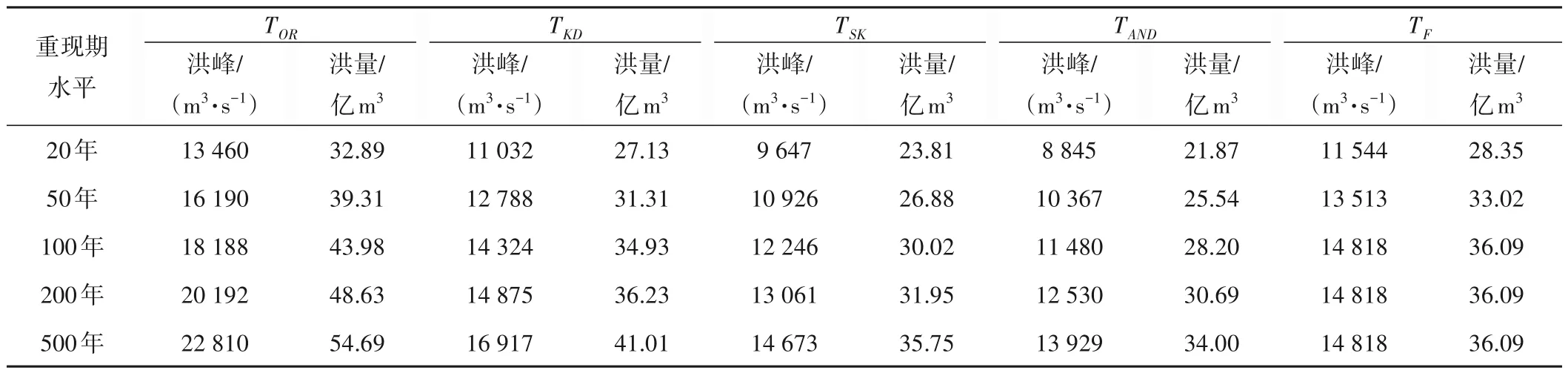
表5 5种重现期的峰量同频组合设计值Tab.5 Design value of peak volume and same frequency combination for five return periods
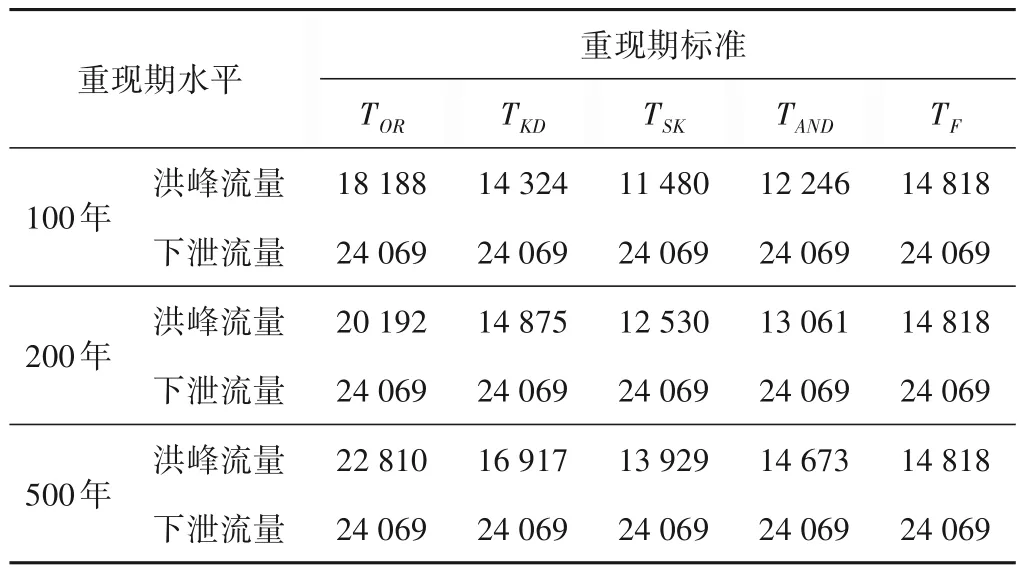
表6 敞泄时下泄流量与各重现期对应洪峰流量的对比 m3/sTab.6 Comparison of open discharge flow and peak flow corresponding to each return period
由以上分析可知,5种二变量重现期都具有各自的特性,不同的二变量重现期标准下,其计算所得的防洪设计值不同,抵御洪水威胁的能力也随之改变。因此,在多变量洪水设计中,重现期标准的选择至关重要。显然,在天然条件下,洪峰、洪量同时更大的峰量组合所得到的水位应更高,但在现有调度规则下,各重现期计算所得的设计水位差别较大,也出现了峰量同时更大,设计水位却相同的情况。
从表7 和表8 可看出,当调洪过程中水库未达到敞泄条件时,相比于防洪重现期,采用同频组合,计算所得的坝上设计水位均满足TOR>TF>TKD>TSK>TAND的规律。即相同重现期水平下,联合重现期计算所得的设计水位最高,抵御洪水威胁的能力最强;同现重现期计算所得的设计水位最低,抵御洪水威胁的能力最弱。二次重现期则位于两者之间,且均小于防洪重现期。而在敞泄的影响下,总体上也呈现未到敞泄条件时的规律,但某些本应随重现期增大而增高的设计水位却相同,这是由于在敞泄时水库的下泄流量均能大于洪水洪峰流量导致的。在敞泄条件下,设计水位186.79 m 对应的防洪重现期水平可包含58~2 695 年一遇,虽然联合重现期计算的水位与防洪重现期相同,但其本身的峰量组合超出防洪重现期相应的组合许多。与此同时,也表明实际工程直接叠加防洪库容所得到的防洪高水位以及设计洪水位为186.80 m 是合理的,能满足防洪标准的要求。
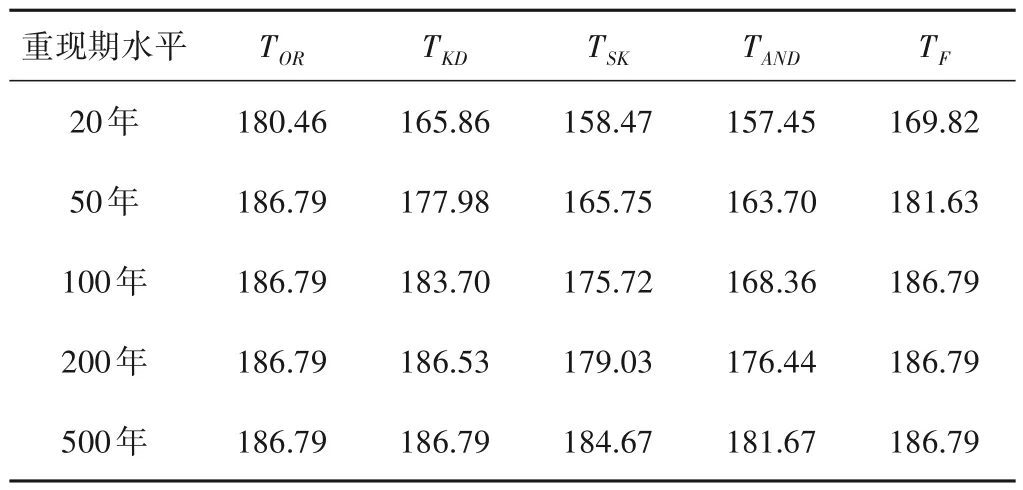
表7 各重现期水平下不同重现期标准的坝上设计水位 mTab.7 Design water level of different return period standards under each return period level
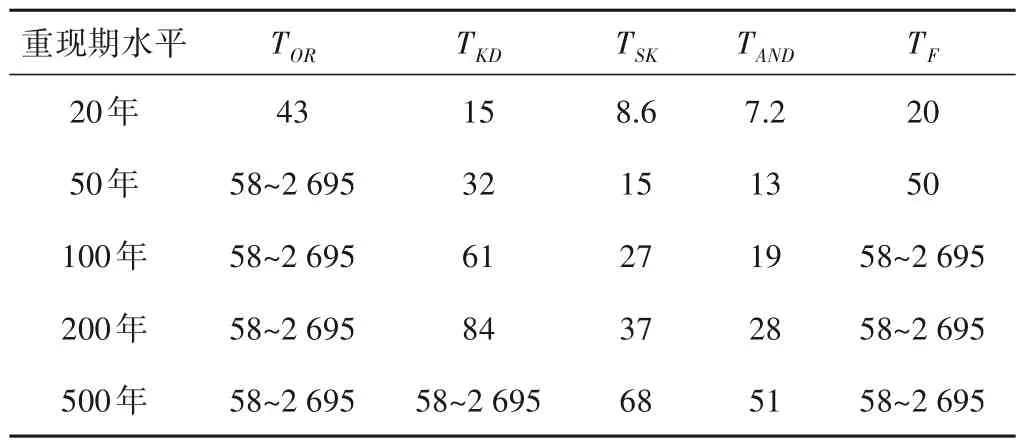
表8 5种不同重现期设计水位对应的设计标准 aTab.8 Design standards corresponding to the design water level in five different return periods
综上所述,联合重现期高估了洪水的风险,以其作为防洪标准的水利工程防洪能力将会溢出,徒增工程成本;同现重现期低估了洪水的风险,以其作为防洪标准的水利工程的防洪能力将会不足,增大工程被洪水破坏的风险。虽然二次重现期相比于首次重现期更为合理,但其本质也仅是从洪水本身特征出发考虑的洪水概率,当工程的行洪界面发生改变后,其抵御洪水威胁的能力依然存在较大的不确定性,其联合设计值是否能满足防洪标准还有待商榷。防洪重现期则充分考虑了洪水与行洪边界的耦合关系,与实际工程密切联系,基于防洪重现期计算所得到的防洪设计值,其防洪能力确定。因此在峰量共同控制作用下的水利工程防洪设计时,以考虑峰量组合与调洪耦合关系的防洪重现期作为设计标准,更符合实际情况。
4 结 论
(1)防洪重现期等值线上的所有组合对应的危险域相同且唯一,计算得到的防洪参数相同,且与工程实际紧密联系,相比传统二变量重现期更为合理;
(2)不同重现期标准下,仅防洪重现期考虑了与工程的实际行洪边界的耦合关系,其形状与传统重现期有较大差异;
(3)不同重现期标准下的设计水位差别较大,且基本满足TOR>TF>TKD>TSK>TAND的规律,仅防洪重现期的防洪能力与防洪标准确定且一致,在水库防洪安全设计中,推荐采用防洪重现期作为多变量重现期的标准。

