重型特种装备车辆多轴协调速度控制方法研究
菊 睿,李孝全,刘海平,张佳丽,张文博
(空军工程大学 防空反导学院,西安 710051)
0 引言
重型特种装备车辆的用途是运输单体超长、超重货物,在军用与民用领域均有应用,具备较优的越野性能与机动性能[1-3],在各种恶劣道路状况下,均可安稳运输货物。但重型特种装备车辆的车体较大,增加了车辆的能耗[4-5],通过研究车辆多轴协调运动轨迹,可有效控制车辆多轴协调运动的位置与速度等相关参数,确保车辆低能耗要求。
罗锦才等[6]以增强学习为基础,设计车辆运动轨迹控制方法,通过三角函数获取轮胎的作用力,以拟合方式得到车辆漂移数据与侧向力,以车辆漂移为目标函数,塑造车辆动力模型,将其变更成2自由度系统,该系统为线性的,通过增强学习法获取该系统内最优控制策略,实现车辆运动轨迹控制,该方法可有效控制车辆运行轨迹,控制效果稳定性较优;杨波等[7]依据规则分配扭矩的思想,设计车辆运动轨迹控制方法,该方法可合理分配车辆扭矩,完成车辆运动轨迹控制,提升车辆驱动系统效率,降低能耗。但是这2种方法均只能实常规车辆的能耗控制,在重型特征装备车辆中,效果较差。
本文中为了能更好地解决非线性关系下的重型特种装备车辆的能耗问题,设计一种最优速度控制模型。研究重型特种装备车辆多轴协调速度控制,达到可降低车辆的能源消耗,提升车辆综合效率的目的。
1 重型特种装备车辆多轴协调运动轨迹
1.1 重型特种装备车辆多轴动力传动能耗问题分析
本文中首先要分析车辆的多轴传动结构,通过分析构造更好地了解能耗的问题。重型特种装备车辆多轴驱动的动力传动系统结构如图1所示。
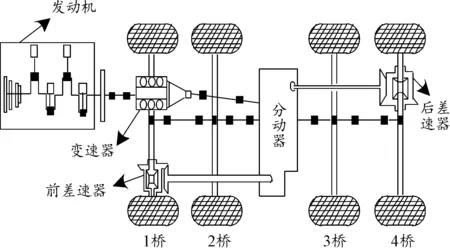
图1 动力传动系统结构Fig.1 Powertrain structure
重型特种装备车辆多轴驱动动力传动系统将发动机输出的扭矩,经由变速器、差速器、分动器与驱动桥,传输到车轮,实现车轮的转动[8-10],变速箱由更改挡位实现其输入输出转速与扭矩的变更,符合繁琐行驶轨迹需求。分动器的作用是依据分扭比为每个驱动桥分配扭矩。差速器的作用是控制两侧驱动轮按照不同角速度运转,完成驱动轮与地面间的纯运转,形成较多的驱动力,加强重型特种装备车辆的机动性。多轴驱动速度合理性是产生能耗的主要部分。
1.2 约束条件计算
通过分析重型特种装备车辆结构,可以看出:车辆多轴传动的速度是否合理,是决定能耗的主要原因。通常学者研究的都是线性曲线的重型特种装备车辆多轴协调速度控制。但在实际的车辆运行条件下,多数车辆是会产生非线性轨迹,非均匀三次B样条曲线,结构简单,使用灵活,得到了广泛的应用。B-spline曲线具备较优的局部控制效果,因此,本文选择非均匀三次B样条曲线,设计传动关系模型。在这之前需要计算约束条件:
车辆多轴传动关系的B-spline曲线表达为:
(1)
其中:车辆多轴传动关系的对应顶点是gi(i=0,1,…,n);k次规范B样条基函数是Ni,k(e);节点矢量的非递减参数是e;e的序列是E:e0≤e1≤…≤ei+k+1,通过U获取k次车辆多轴传动关系的分段多项式。
B-spline曲线的递推公式为:
(2)
当ei≤e≤ei+1时,Ni,0(e)=1,否则,Ni,0(e)=0。
通过式(2)可获取不同次数时的B-spline曲线表达式。分析重型特种装备车辆多轴传动关系时,需同时考虑车辆的速度与加速度等约束条件,并递推传动关系为:
(3)
其中,l=1,2,…,k;j=i-k+1,…,i。
重型特种装备车辆多轴传动关系分析时,速度与加速度为不间断的,因此选取三次B样条曲线展开插值,获取车辆多轴协调传动关系控制顶点的一阶导数:
(4)
其中,插值系数是λ,根据人工经验设定,一般为1。车辆多轴协调传动关系的控制顶点的二阶导数:
(5)
结合式(3)—式(5)可获取重型特种装备车辆多轴协调运动时的速度与加速度作为约束条件:
(6)
(7)
车辆多轴协调运动时需符合的速度约束条件:
|q1(e)|=|v(e)|≤vmax
(8)
其中,符合车辆多轴协调运动需求的最大速度是vmax。车辆多轴协调运动时需符合的速度约束条件为:
|q2(e)|=|a(e)|≤amax
(9)
1.3 车辆多轴间的传动关系模型计算
重型特种装备车辆多轴传动关系属于非线性运动,电子凸轮能够在主轴与从轴间完成非线性传动[11],与重型特种装备车辆多轴协调运动形式相同,为此,依据电子凸轮的虚拟主轴与从轴的传动原理[12-13],建立重型特种装备车辆多轴传动关系模型。
利用三次样条插值法(三次样条插值是通过一系列形值点的一条光滑曲线,数学上通过求解三弯矩方程组得出曲线函数组的过程。实际计算时还需要引入边界条件才能完成计算。一般的计算方法都没有说明非扭结边界的定义,但数值计算软件如Matlab都把非扭结边界条件作为默认的边界条件。)构造虚拟主轴和从轴间的传动关系模型;三次样条插值电子凸轮表内,代表车辆多轴协调运动轨迹的数个控制顶点,确保表内运动轨迹控制顶点位置存在二阶不间断导数,运动轨迹控制顶点间的区间是三次多项式,因此,建立获取的三次样条插值多项式函数h(g),对于电子凸轮表模型存在以下关系:h(g)在虚拟主轴各运动轨迹控制顶点间的区间Ii=[gi-1,gi]内均为三次多项式,h(g)在全区间[x0,xn]内存在2次不间断导数,针对随机运动轨迹控制顶点,其传动关系式为:
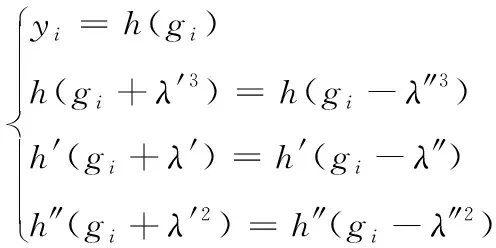
(10)
其中:车辆从轴位置是yi;车辆主轴位置是gi;前插系数是λ′;后插系数是λ″;h(g)的一阶导数是h′(g);h(g)的二阶导数是h″(g)。
1.4 车辆多轴间的传动关系模型计算
依据1.2小节获取的约束条件和1.3小节获取的车辆多轴传动关系参数,利用S形速度控制算法得到最优速度控制模型。
S形速度控制算法是对重型特种装备车辆多轴运动不同阶段的速度进行控制。
1) 车辆不同轴最大速度控制
在车辆运动处于加加速段o1时,需确保车辆主轴运动通过o1后,其他轴速度需小于最大设置速度F,因为o1能够直接决定减加速段o3,所以需保证当前车辆主轴运动速度经过o3后的速度低于F[14]。
令车辆主轴运动处于o1的某个周期时,其当下加速度是a,速度是v,通过1.2小节获取,进入o3后,经过第i′周期,车辆不同轴运动的相互关系为::
(11)
其中,o3的周期数是b3,则结束后处于的最大速度vmax为:
(12)
通过式(13)可求解o1内随机周期内车辆多轴运动可达到的vmax,当下一周期符合vmax>F,那么进入o3,通过S形速度控制算法可确保车辆多轴运动达到vmax后保持不变。
2) 车辆多轴运动的减速控制
通过提前减速的方式,确保车辆精准停至目标位置,车辆多轴运动减速处理的重点是:多轴运动速度曲线离散化后[15],精准求解减速距离L,就是分析车辆多轴运动速度控制的各周期中,L和剩余距离Lγ的大小,令车辆多轴运动减速段的周期数是b5、b6、b7,分别对应加减速段o5、匀减速段o6、减减速段o7。
利用1.2小节重新求解车辆多轴运动进入o5时的加速度a′,依据式(13)获取的vmax求解o5结束后,第b5个周期时,车辆多轴运动的加速度、速度与运行距离为:
ab5(e)=-a′(e)·b5
(13)
(14)
(15)
第b6个周期时,车辆多轴运动的加速度、速度与运行距离为:
ab6(e)=ab5(e)
(16)
vb6(e)=vb5(e)+ab5(e)·b6
(17)
(18)
第b7个周期时,车辆多轴运动的加速度、速度与运行距离为:
ab7(e)=-a′(e)·b7
(19)
(20)
(21)
结合式(16)、式(19)、式(22)获取,车辆多轴运动处于减速段时的运行距离即减速段距离为:
L=Lb5+Lb6+Lb7
(22)
车辆多轴运动的减速距离既包含L,还包含减加速段距离L3,通过求和式(12)获取车辆多轴运动进入o3时的L3为:
(23)
因此,车辆多轴运动减速段的距离是L′=L+L3。通过控制L′实现重型特种车辆多轴运动的减速处理。通过S形速度控制算法实现车辆多轴运动的最大速度处理与减速处理,完成车辆多轴运动的最优速度控制。
2 测试实验及结果分析
2.1 实验模拟环境建立
以某重型特种装备车辆为实验对象,该车辆的发动机是高速四冲程的8缸发动机;分动器包含高低档,重型特种装备车辆行驶过程中使用高档;差速器选择对称式圆锥行星齿轮差速器;变速器由固定轴式主变速器和行星轮式变速器构建而成。利用本文方法控制该车辆多轴协调运动轨迹,验证本文方法多轴协调运动轨迹的控制效果。实验模拟环境如图2所示。

图2 实验模拟环境Fig.2 Experimental simulation environment
2.2 Trucksim软件计算参数
选定车型开始在Trucksim中建立整车模型。详细参数计算后设置如表1所示。
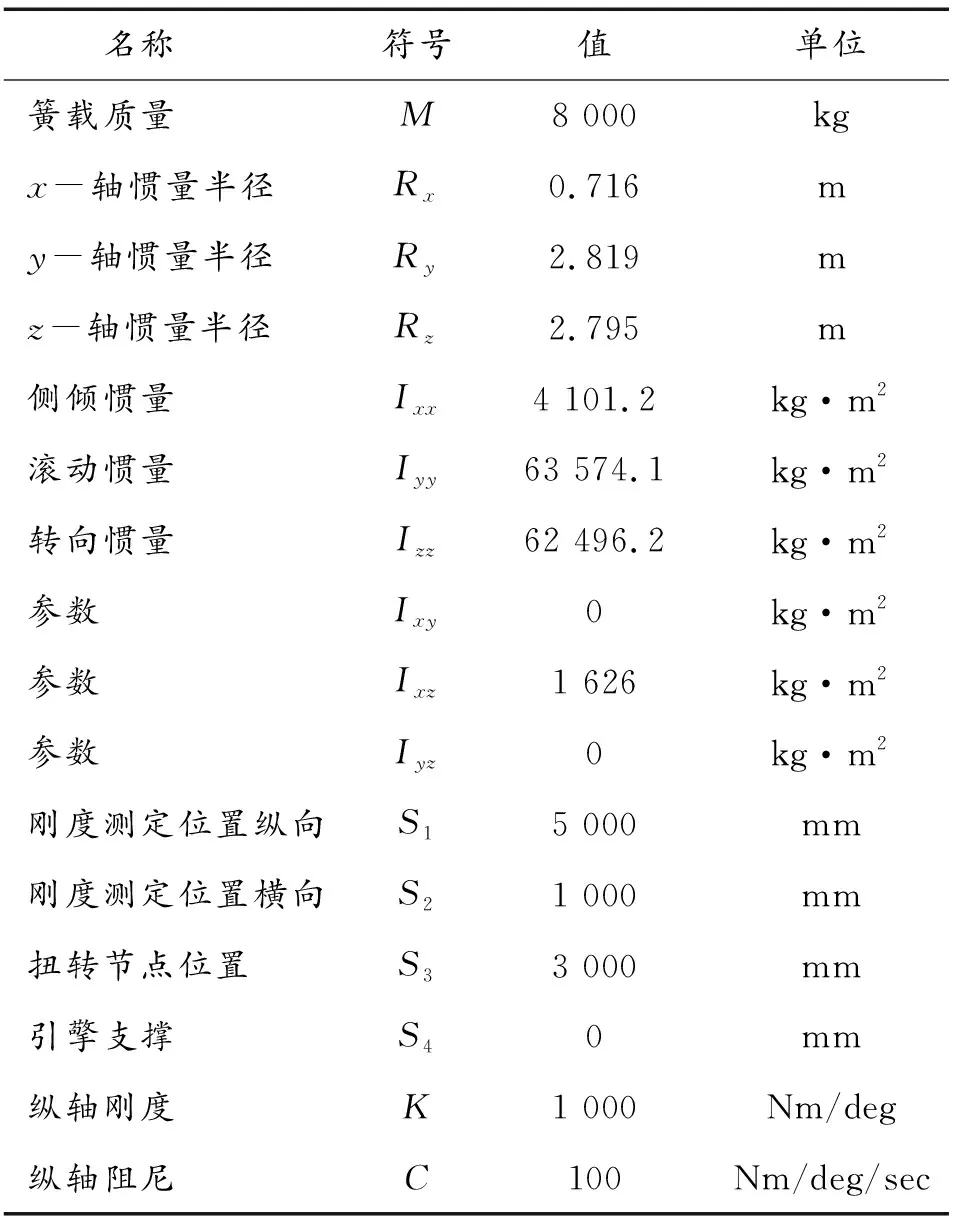
表1 整车建模仿真基本尺寸Table 1 Basic dimensions of vehicle modeling and simulation
设置实验初始参数,具体参数表2所示。
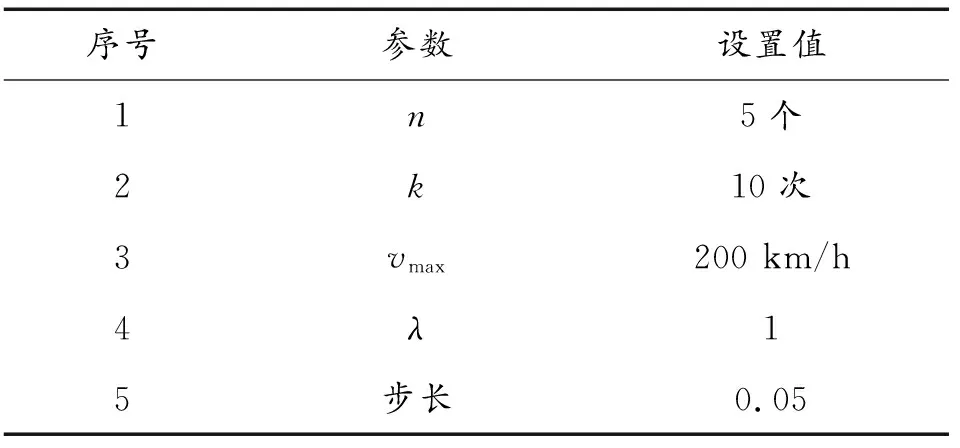
表2 实验参数初始设置Table 2 Initial setting of experimental parameters
设定车辆规定轨迹,其轨迹如图3所示。
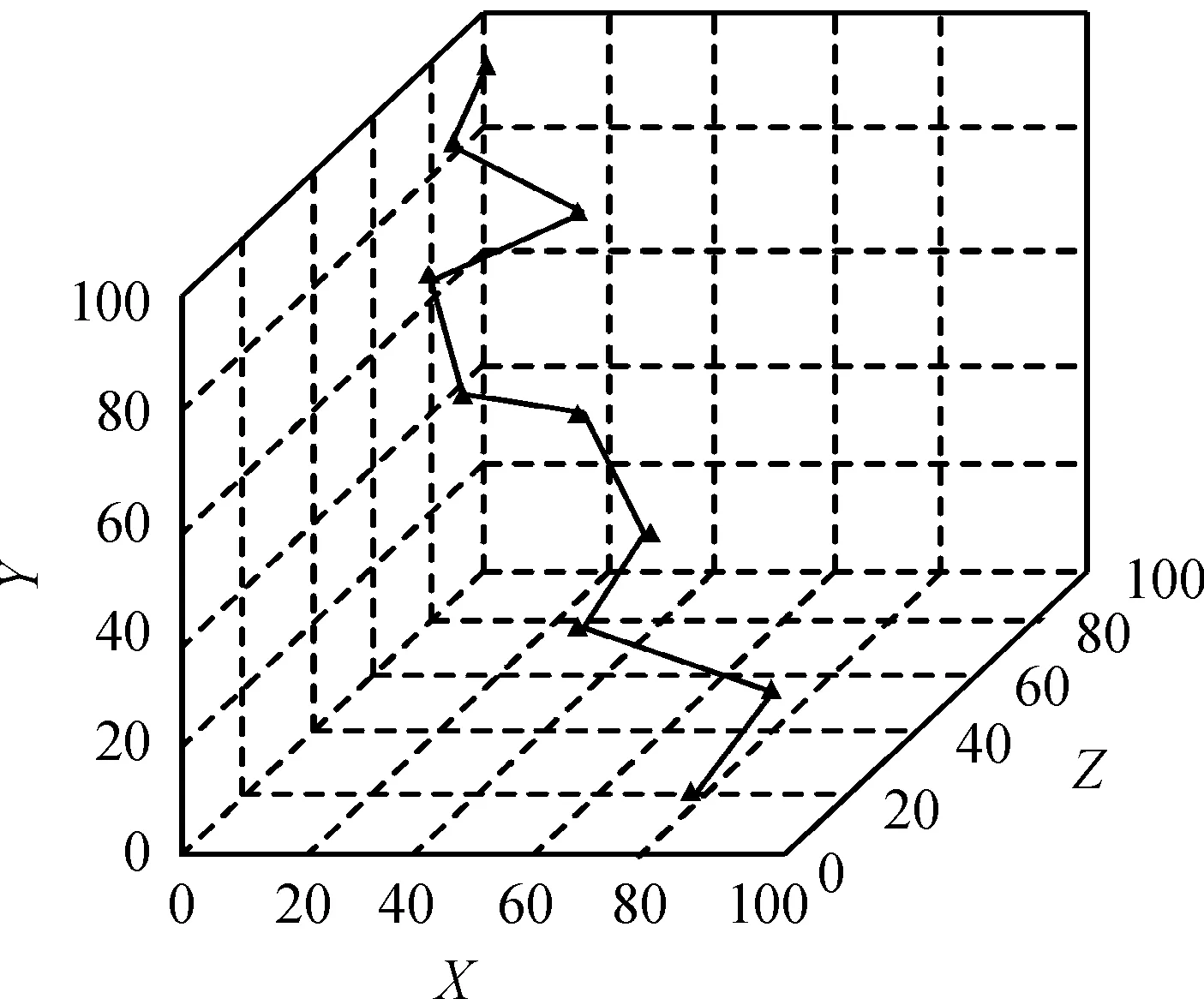
图3 车辆规定轨迹图Fig.3 Vehicle prescribed trajectory map
2.3 利用Simulink仿真实验
利用Simulink进行车辆多轴协调运动轨迹控制的仿真实验,Simulink是Matlab仿真软件内一个图形化仿真工具,具备动态系统建模、仿真与分析功能。Simulink支持离散系统与线性系统等系统的仿真,具备可视化与开放性等优势。
利用Simulink设置该车辆多轴协调运动为周期性运动,车辆位移目标位置40 000。利用本文方法、文献[6]中的方法和文献[7]中的方法控制该重型特种装备车辆多轴协调运动轨迹,令车辆达到目标位置,该车辆主从轴的位置、速度与加速度控制结果如图4和图5所示。

图4 不同方法主轴加速度控制曲线Fig.4 Spindle acceleration control curves of different methods
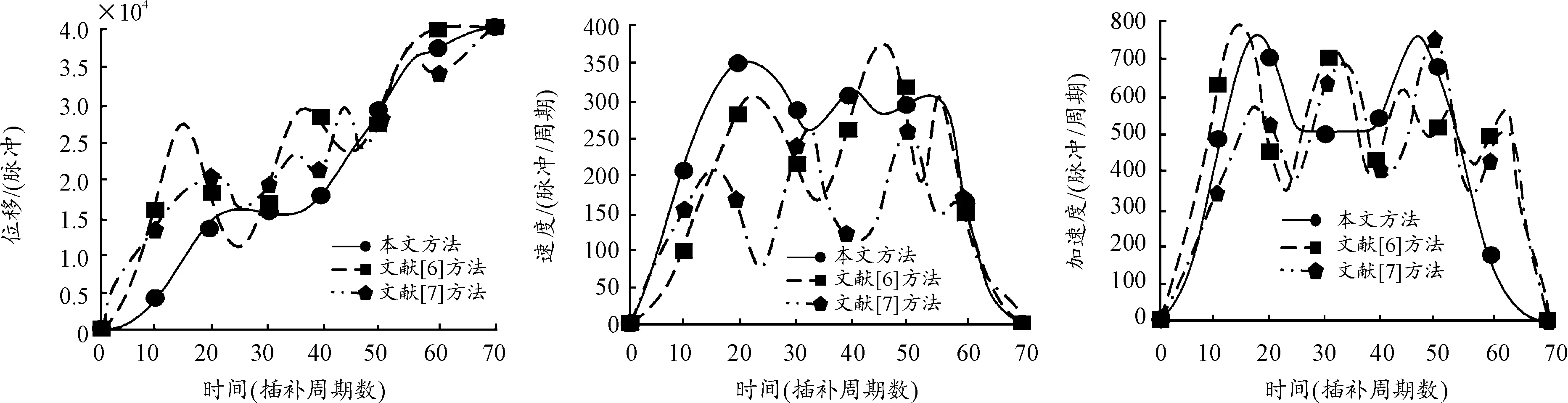
图5 不同方法从轴位置、速度与加速度控制曲线Fig.5 Different methods to control the curve from axis position,velocity and acceleration
根据图4和图5可知,3种方法控制后的车辆主从轴位移均能达到目标位置,但是本文方法的车辆主从轴协调控制过程中,速度与加速度曲线满足S形的速度与加速度控制需求,且从轴速度与加速度的变化情况较平稳,无过多波动,同时没有突变情况发生,但是对比方法虽然到达了目标位置,但是在控制过程中,位置波动较大,并且速度与加速度的变化情况不佳,出现多次明显波动,不够平稳。实验证明:本文方法可有效控制重型特种装备车辆多轴协调运动过程中的位移、速度与加速度,其具备了有效性。
利用Simulink设置该车辆多轴协调运动为非周期性运动,车辆位移轨迹按照图3规划轨迹设置,分析3种方法在控制车辆多轴协调非周期性运动的运动轨迹,控制结果如图6所示。
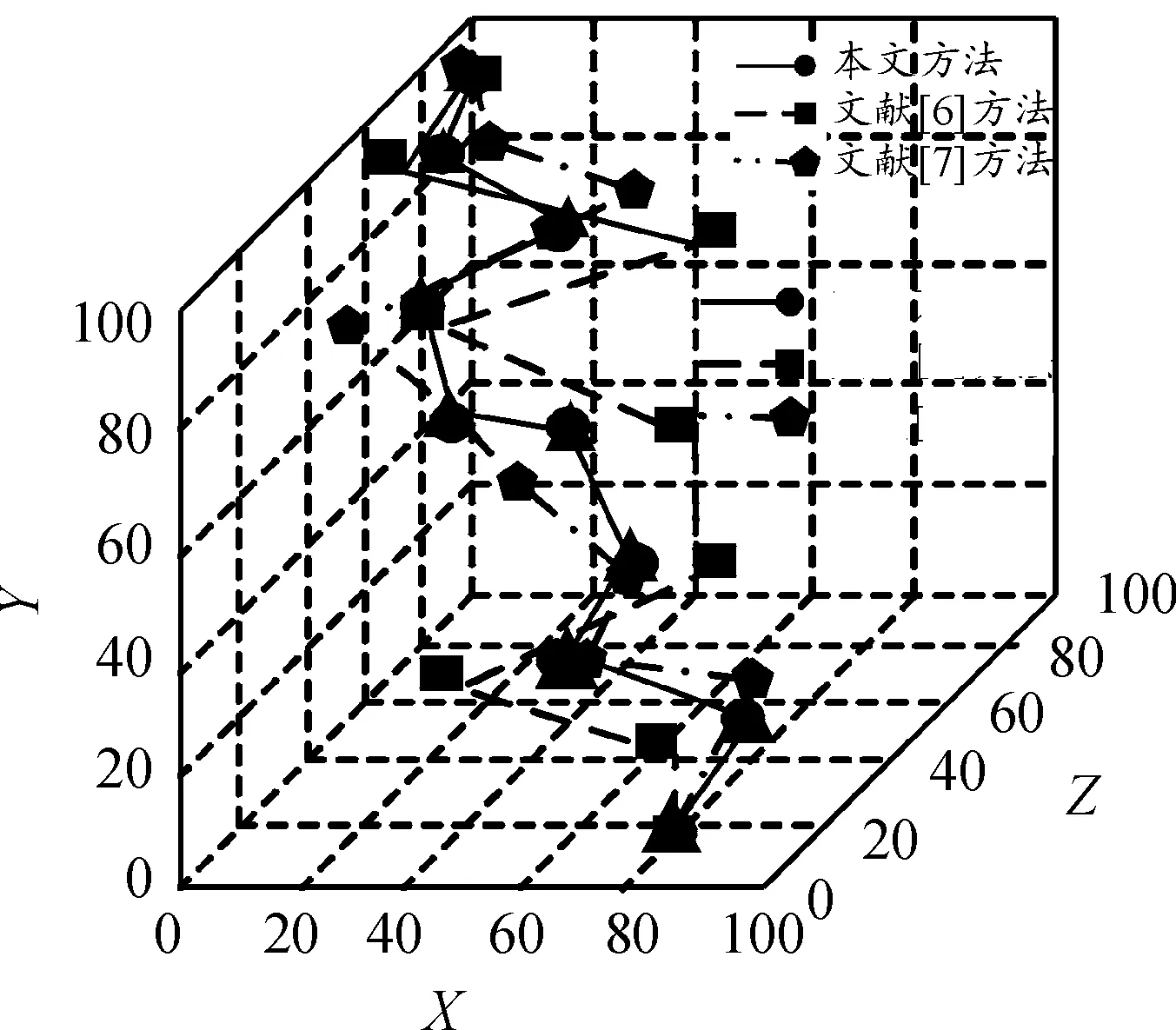
图6 车辆多轴协调非周期性运动轨迹控制结果Fig.6 Control results of vehicle multi-axis coordinated aperiodic motion trajectory
根据图6可知,本文方法可有效控制车辆多轴协调非周期性运动的运动轨迹,其控制后的运动轨迹与轨迹运动轨迹差距非常小,控制后的轨迹和规定轨迹基本一致,确保车辆达到了目标位置,但是对比方法均出现了较大的误差,其运动轨迹与规定轨迹部分重合,但是多数位置均偏离规定轨迹。实验证明:本文方法的轨迹控制最准确,其可精准控制车辆多轴协调非周期运动轨迹,有效提高了控制效果。
利用Simulink分析该车辆应用3种方法控制多轴协调运动轨迹后,车辆的综合效率、百公里油耗与节油率,分析结果如表3所示。
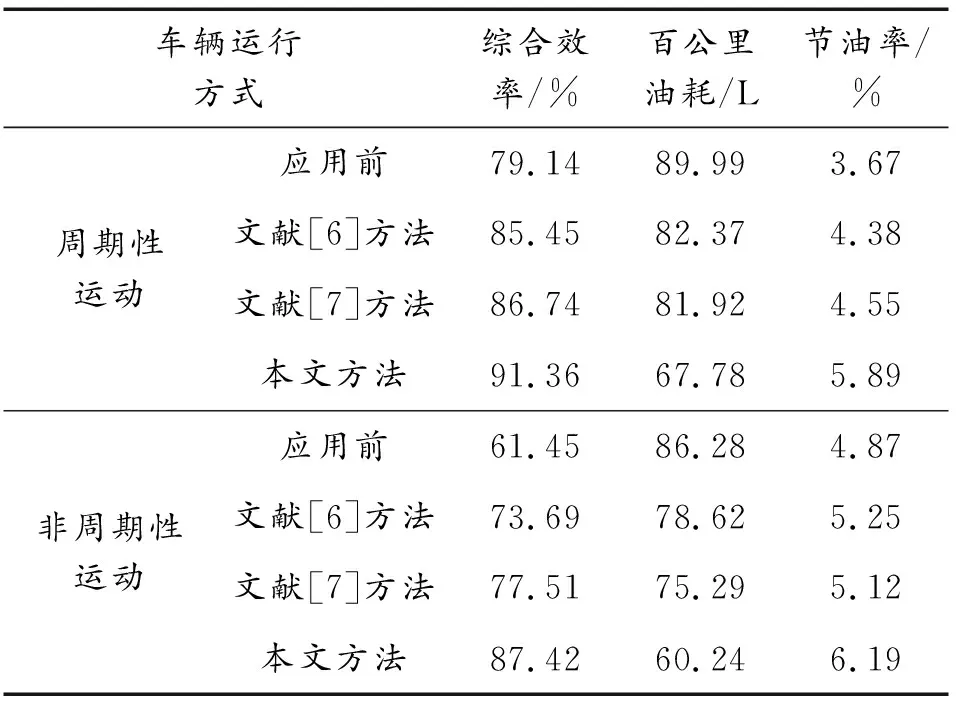
表3 综合效率、百公里油耗与节油率分析结果Table 3 Analysis results of comprehensive efficiency,fuel consumption per 100 kilometers and fuel saving rate
根据表3可知,在车辆处于周期性运动与非周期性运动时,应用本文方法后车辆的综合效率均有所提升,百公里油耗均显著下降,节油率均明显提升,文献方法在三方面也有一定幅度的提升,但是其提升幅度远远低于本文方法。实验证明:应用本文方法后,可有效降低车辆的能源消耗,提升车辆综合效率。
3 结论
依据重型特种装备车辆多轴协调动力传动系统的传动特性,研究重型特种装备车辆多轴协调运动轨迹,合理控制车辆多轴协调运动轨迹,确保车辆到达指定位置,降低车辆能源消耗。仿真实验部分,主要工作如下:
1) 仿真实验首先利用Trucksim软件计算参数。得到了整车建模的相关参数和数据。
2) 利用Simulink进行车辆多轴协调运动轨迹控制的仿真实验,令车辆达到目标位置,测量该车辆主从轴的位置、速度与加速度控制结果。
3) 通过仿真实验验证了本文方法车辆多轴协调运动轨迹控制的有效性。设计车辆多轴协调运动轨迹控制方法,可促进重型特种装备车辆的发展,扩展其应用领域。

