基于强化蚁群算法的机器人路径规划研究
陈丹凤,雷 昊,刘俊朗,何 俊
(佛山科学技术学院 机电工程与自动化学院, 广东 佛山 528225)
0 引言
蚁群算法(ant colony optimization,ACO)要追溯到20世纪90年代,由意大利学者M.Dorigo等人提出。最初被用于旅行商问题(travelling salesman problem,TSP)的求解。蚁群算法与遗传算法、模拟退火等优化算法相似,都源于大自然生物习性的启迪。蚁群算法模拟的是蚂蚁觅食过程中,蚂蚁之间建立起的信息素机制,从而确立蚁穴与食物之间的最优路径,并对路径形成记忆的过程。由于该算法具有良好的鲁棒性、记忆性、适合复杂问题求解等优点,被广泛用于优化问题[1]、路径规划问题中[2]。
但蚁群算法在规划路径的过程中,也面临一些问题。如算法初始参数的选取严格依赖于经验,相同的初始参数下,参数配置过程随机性强,因此制约了算法的收敛性、快速性等性能。此外,蚁群算法也面临着陷入局部最优及迭代停滞等现象。针对上述问题,近年来学者们展开了大量的理论及实践研究[3-4]。
张松灿等[5]讨论了蚁群算法在移动机器人路径规划中的应用问题,详细分析了蚁群算法的工作原理及其缺陷。由于蚁群算法参数较多,且参数之间存在紧密的耦合作用,论文中算法的参数配置过程相对复杂,不便于实际应用。马铭希等[6]为了缩短最优路径的搜索时间,提高搜索效率,提出使用人工鱼群的视觉探测和规避障碍的机制优化蚁群算法。该算法融合了人工鱼群算法的搜索策略,同时利用logistic混沌模型对全局信息素进行筛选。算法通过改进搜索策略提高了搜索效率。向永靖等[7]针对蚁群算法参数多,且不同参数组合影响算法的全局收敛性和收敛速度的难点,对蚁群算法的参数选择进行了研究,并通过试验验证,获取了各个参数较为理想的取值范围,以此减少了算法执行过程中参数配置所需时间。但上述研究,均忽略了算法参数与参数之间的耦合作用,致使算法迭代次数过多,时间过长,甚至会出现不收敛的情况。在文献[8]中,马小陆等提出了基于势场跳点的蚁群算法。该算法通过跳点,大大减少了最优路径搜索过程中转折点的数量,从而提升了算法收敛速度,也在一定程度上避免了陷入局部最优的情况。但论文没有对改进蚁群算法的参数设定过程进行讨论。此外,势场蚁群算法增加了算法的参数数量,也将在一定程度上影响算法的收敛性。
截至目前,国内外研究中常用的蚁群优化算法,如粒子群算法[9],自适应方法[10-11]、人工势场算法(artificial potential field algorithm,APFA)、A*[12],遗传算法[13]等,算法中都包含大量的参数,涉及到复杂的参数配置过程,而往往这些算法在执行过程中,大多通过实验来确定参数的较优范围,以此作为经验参数,同时也忽略了参数与参数之间的耦合作用。而当参数选取不佳或者缺少经验时,会导致算法的效果较差,甚至出现无法找到最优解、收敛迭代次数及时间过长等问题。
此外,无论如何改进算法,一旦改进算法在原算法基础上引入了新的参数,都避免不了参数配置过程对算法收敛速度的影响,会使得算法对经验值的依赖以及参数配置过程复杂的问题更明显。近年来,面对算法执行过程中参数的选择、参数的优化等问题,学者们也展开了诸多研究。
强化学习算法(RL)可在模型参数未知的情况下,通过设置适当的状态及动作从环境中获取参数信息,即RL算法能通过学习策略实现参数的自适应调整。有学者发现,使用强化学习辅助进化算法(evolutionary algorithm,EA)进行参数调节是一种可行且有效的方法[14]。
在文献[17-18]中,作者使用强化学习对粒子群算法(particle swarm optimizer,PSO)进行改进,通过引入强化学习作为策略控制机制,允许算法自动确定更新策略,以此消除人工控制过程的不确定性,提升算法在复杂环境下的搜索能力。
严家政等[15]使用强化学习(reinforcement learning,RL)方法对水箱的PID控制系统实现了算法参数的自整定及优化。该方法将参数优化问题近似为求解约束优化问题,再通过强化学习的试错机制、经验回放机制等对参数进行在线自整定及优化处理。结果表明,强化学习在参数优化及参数自整定问题上,能够有效减少调参时间,并避免因缺乏经验导致的调参效果不理想等问题。
在文献[16]中,Feng Wang等人使用强化学习算法解决大规模的优化问题。为了提高算法的搜索效率,提出一种用于级别数控制的强化学习策略。该方法是一种有效的自适应调整技术,通过实验验证,该方法在大规模解空间中能更有效地搜索更好的结果。
受上述研究的启发,针对蚁群算法参数多且配置过程依赖经验值、随机性强、参数之间耦合性强的问题,提出一种基于强化学习和人工势场算法改进的蚁群算法。首先,提出强化蚁群算法(RL-ACO),基于强化学习对蚁群算法的参数配置过程进行学习和优化,以此获取蚁群算法的参数。该过程将在无经验值的条件下进行,摆脱算法对经验参数的依赖。其次,引入人工势场算法的局部优化机制,对算法的局部路径进行再规划,通过减少路径中的拐点数目增强算法避障能力,降低算法陷入局部最优几率的同时,提高路径平滑程度和最优路径搜索速度。最后,通过不同维度的栅格构建机器人工作环境,应用改进前后的蚁群算法进行路径规划研究,进一步验证本文所改进算法在迭代次数、收敛速度以及路径平滑程度方面的优势。
1 地图环境建模
在进行路径规划问题求解之前,需要对当前障碍物地图环境进行模型构建。常用的建模方法有可视化图法、拓扑法、栅格法[19]和广义锥法等。与其他方法相比,栅格法具有结构简单、易于理解实现、数据存储直观、模型精度可调以及网格划分精度高等优点。因此,本文中选择使用栅格法来构建机器人的工作环境。通常,在网格环境建模中,0值表示环境地图中的自由区域,相应的网格填充为白色;而1值表示环境地图中的障碍区域,相应的网格用黑色填充。
环境模型构建的基本思想可以描述为:
1) 使用信息采集设备获取工作环境中的环境信息。
2) 将机器人的实际工作环境简化为二维有限运动区域,以该区域左下角为坐标原点,以其水平方向为X轴,垂直方向为Y轴,建立直角坐标系。
3) 对机器人的二维有限运动区域进行网格化处理,绘制障碍物网格并赋予编号。
如图1所示,空白栅格代表可移动空间,黑色栅格表示障碍物空间,按照从左到右自下而上的规律依次对栅格进行编号,每个栅格对应唯一的编号。

图1 栅格法位置编号Fig.1 Position marker of raster method
2 改进的蚁群算法
2.1 蚁群算法基本原理
作为一种启发式搜索算法,蚁群算法具有良好的鲁棒性,且易于融合其他算法应用到实际问题中。该算法可以理解为一种用来搜索最优路径的概率型算法,描述的是蚂蚁在觅食过程中会在路径上留下信息素类物质,并通过对信息素类物质强度的感知,指导自己搜索行为的方向。蚂蚁觅食的过程是一个正反馈的过程:某路段经过的蚂蚁越多,留下的信息素就越多,浓度越高,进而引导更多的蚂蚁选择该路段,最终促使蚂蚁找到一条最短的觅食路径。蚁群算法的执行过程如图2所示。

图2 蚁群算法流程Fig.2 Ant colony algorithm flow
根据这种信息素机制,意大利学者M.Dorigo对蚂蚁的选路规律进行了研究,并采用状态转移概率公式来刻画该过程,如式(1)所示。

(1)
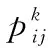
(2)
在模拟蚁群寻找最优路径的过程中,式(1)指导着蚂蚁下一节点的方向,同时在概率转移公式作用下,蚂蚁k从节点i移动到节点j后,将会通过式(3)更新蚂蚁走过路线的信息素浓度:
τij(t+n)=(1-ρ)τij(t)+Δτij(t)
(3)
具体而言,式(3)意味着当蚂蚁从第i个网格走到第j个网格时局部信息素的更新;而当所有蚂蚁执行迭代搜索时,信息素将依据式(4)和式(5)进行全局更新:
(4)
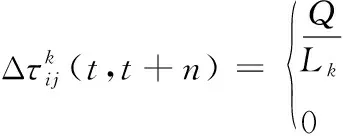
(5)
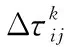
2.2 强化蚁群算法(RL-ACO)
上述蚁群算法在执行过程中,诸多参数的配置过程往往依赖经验或者采用多次试验获取。但这一过程随机性强,对经验依赖性强。
为了改善传统蚁群算法对参数的依赖以及参数配置过程繁杂随机的现状,本文中提出一种强化蚁群算法(RL-ACO)。主要利用强化学习中Q-Learning方法的决策能力,对蚁群算法中的信息素启发权重因子和距离启发权重因子进行组合优化,将算法路径最优性、路径时效性以及路径收敛性作为参数配置的评价指标,建立参数寻优策略,求解与环境交互过程中最优策略Q值,以获得一组较理想的参数取值,最终以更快的收敛速度和最少的迭代次数搜索到最优路径。过程中,将ACO算法中的信息素启发权重因子与距离启发权重因子的改变范围作为动作空间,同时设定步长为0.1,以最大化奖赏为目标计算Q值,如式(6)所示。
Q(aα,l,aβ,l)=maxRt+1
(6)
其中,
Rt=rt+art+1+a2rt+2+…+a
(7)
Rt=rt+aRt+1
(8)
式(7)、式(8)中:rt+1为执行完动作后的奖励;α为折扣因子,通常在区间(0,1)内取值;Rt为多步的回报。
算法执行过程中,具体的参数选定及优化流程所述如下:
1) 以信息素启发权重因子α和距离启发权重因子β构建参数向量W(W=[α,β]T),并以W为参数优化目标,同时设置参数搜索范围F,随机初始化参数向量W0,设定W中α和β的变化步长为0.1。
2) 根据奖赏值选择α和β的动作,并获取最新参数向量W输入下,算法在收敛迭代次数V和最优步长B的响应数据,并构建V和B的奖励函数。
3) 根据步骤2中的奖励函数计算Q值,并将其存入历史数据集H中。
4) 根据历史数据集H近5次的数据差异,判断是否满足停止迭代条件,若满足,则终止迭代,输出最优参数配置W,若不满足,则返回步骤2)。
在实验中,为了增加优化参数W的准确性,对近5次的响应数据进行提取,计算近5次数据的变化率,以此评估参数配置过程的平稳性,并将其作为参数配置结果是否达到最优的判断条件。当近5次数据的变化率小于一定阈值时,即可认定已到达最优参数配置。
对应的算法流程如图3所示。

图3 RL-ACO算法流程Fig.3 Flowchart for RL-ACO
2.3 局部优化机制下的强化蚁群算法
基于强化学习改进的蚁群算法,在全局路径规划中具备良好的收敛速度,且具备在较少迭代次数下搜索到最优路径的能力。但面对高维复杂障碍物环境下的路径规划问题,特别是前进方向上障碍物较多,且距离障碍物位置过近时,所搜索的最优路径存在拐点多,路径曲折的现象,表明RL-ACO算法的局部轨迹规划能力有限。
为此,本文中进一步引入人工势场算法(APF)的局部优化机制对强化蚁群算法进行局部轨迹优化,旨在减少轨迹非必要转折点数目的同时,提高轨迹的平滑度,以此提升最优轨迹的搜索速度。具体通过构建一个虚拟的力场来增加当前节点与目标节点之间的引力,使得机器人能够更快地到达目标点,从而缩短轨迹规划过程。其中,引力势场函数如式(9)所示。
(9)
式(9)中:k表示引力势场常数;Xi为当前机器人节点位置;Xg为目标点节点位置。进而以引力势场的负梯度作为目标点与机器人之间的引力,计算函数如式(10)所示。
Fatt= -grad (Uatt) = -k(Xi-Xg)
(10)
同时,通过机器人当前位置与周围环境中障碍物位置的斥力势场,构建机器人与障碍物的排斥关系,以改善机器人在路径规划过程中的避障效果,提高规划路径的安全性和平稳程度。斥力势场函数如式(11)所示。
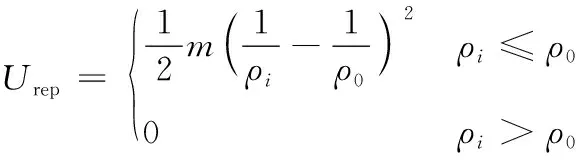
(11)
式(11)中:m为斥力场函数系数;ρi为机器人当前位置与障碍物位置的距离。当前位置与障碍物位置大于阈值ρ0时,认定该障碍物对机器人当前位置不存在碰撞风险,故该障碍物对当前位置的斥力作用消失;而当前位置与障碍物位置小于阈值ρ0时,通过式(11)计算阈值内斥力势场,并类比重力势场数学模型,获取斥力确定值,计算过程如式(12)所示。
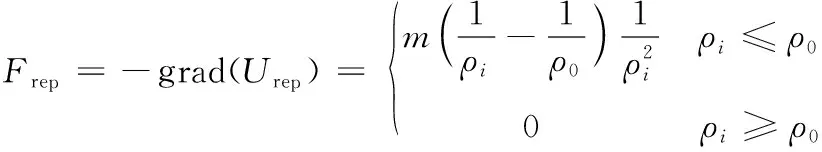
(12)
斥力与引力计算方式类似,在此不再赘述。机器人在当前位置受到目标点引力及阈值内障碍物斥力的合力,如式(13)所示。
Ftot=Fatt+Frep
(13)
基于上述过程,进一步利用APF的势场机制对强化蚁群算法进行临近拐点之间局部路径再规划。算法的具体执行过程如下:
1) 基于RL-ACO算法进行不同维度下栅格地图的全局路径规划。
2) 提取全局最优路径中的拐点数据。
3) 判断并筛选拐点数据中距离小于阈值的相邻拐点对。
4) 调用APF算法对小于阈值的相邻拐点对进行局部路径再规划,并更新拐点位置数据,同时保持大于阈值的拐点对位置数据不变。
5) 判断再规划后的局部路径是否与原路径重合,若是,则认定当前路径为最优规划路径,否则,更新路径信息并返回步骤3)。
优化流程如图4所示。
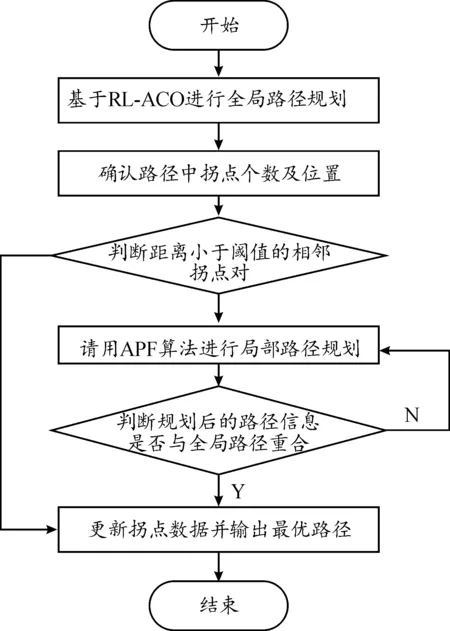
图4 局部优化机制下的强化蚁群算法Fig.4 Enhanced ant colony algorithm under local optimization mechanism
3 实验验证
为了验证RL-ACO算法在收敛性、收敛速度等方面的优势,将从不同维度栅格地图进行路径规划仿真实验。
实验过程中,ACO算法以及RL-ACO算法的参数配置如表1所示。通过文献[20]可知,信息素启发权重因子α和距离启发权重因子β的取值对算法的性能有较大的影响。因此,本实验选取α和β这组参数作为待强化学习的目标参数。表1中α和β在不考虑经验值的前提上,经RL-ACO算法中的强化学习自主参数配置获取,对ACO算法而言,表1中所有的参数取值都源于经验值,其余参数取自经验值。

表1 算法的参数配置Table 1 Parameter configuration of ACO and RL-ACO
基于表1所示的参数配置,进一步对15×15、20×20、30×30三种随机设置的栅格环境下的路径规划问题进行对比分析。首先,分别对ACO和RL-ACO算法在15×15的低维栅格地图上进行仿真实验,结果如图5所示。
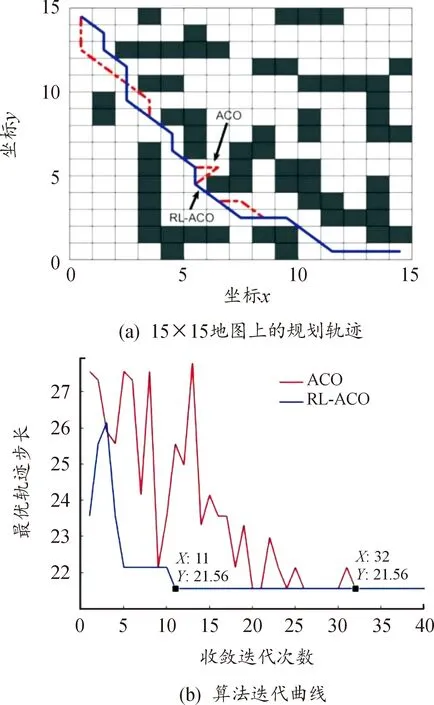
图5 15×15地图上的规划轨迹(a)和算法迭代曲线(b)Fig.5 Planning trajectory on a 15×15 map (a) and comparison of algorithm iteration curves(b)
由规划轨迹图5(a)可知,ACO算法和RL-ACO算法都能够较好较快的解决小规模路径规划问题。从收敛曲线图5(b)可知小规模问题的求解上,RL-ACO方法能够通过更少的迭代次数收敛到最优路径。
2种算法的路径长度和迭代次数如表2所示。表明在低维度路径规划问题中,改进的RL-ACO算法能有效降低迭代次数。

表2 15×15栅格地图上的运行结果Table 2 Run results on 15×15 raster map
进一步在20×20的栅格地图上对比ACO与RL-ACO路径规划效果。
由规划轨迹图6(a)可知,相较于ACO,RL-ACO算法规划的轨迹减少了20%的转折点数,避免了路径规划中不必要的转折所带来规划路径长度的增加,由收敛曲线图6(b)可知,RL-ACO算法快速收敛到最优路径长度,ACO算法虽能找到最优路径,但结果存在波动,且最终收敛迭代次数过大。ACO算法在高纬度问题求解上的劣势初步显现。表3所示2种算法的路径长度以及收敛迭代次数再次验证上述结论。
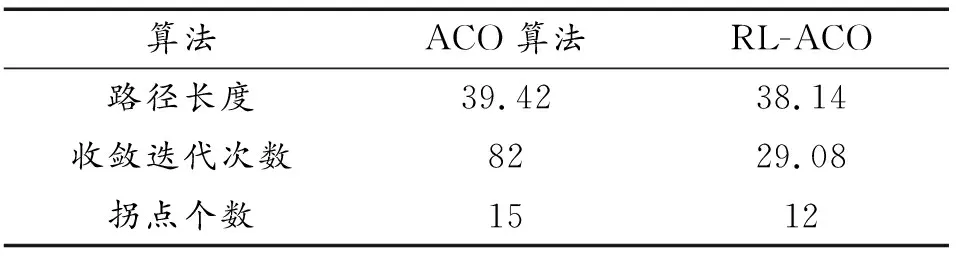
表3 20×20栅格地图上的运行结果Table 3 Run results on 20×20 raster map

图6 20×20地图上的规划轨迹(a)和算法迭代曲线(b)Fig.6 Planning trajectory on a 20×20 map (a) and comparison of algorithm iteration curves(b)
最后,对比ACO与RL-ACO在30×30的栅格地图上的路径规划效果。
当地图维度增加至30×30时,由图7(a)和表4的数据可知,相较ACO算法,RL-ACO算法规划的最优路径转折点数目减少了近40%。结合图7(b)和表4可知,ACO算法在有限的迭代次数中,收敛迭代次数不具稳定性,且最优步长不具确定性。而RL-ACO能快速收敛到最优步长,并有效的减少蚁群算法的收敛迭代次数。对ACO算法在规定的迭代次数内无法搜索到最优规划路径,暴露出不以具体环境调整算法参数设置致使迭代收敛速度慢,在复杂环境下寻优能力弱的问题。本文中提出使用强化学习优化参数配置的方法很好的解决了在中高维度问题求解中该方面的问题。

表4 30×30栅格地图上的运行结果Table 4 Run results on 30×30 raster map

图7 30×30地图上的规划轨迹(a)和算法迭代曲线(b)Fig.7 Planning trajectory on a 30×30 map (a) and comparison of algorithm iteration curves(b)
通过对比算法在不同维度地图中路径规划的最优路径长度、初次找到最优路径的迭代次数等数据,验证了改进方法能有效减少最优路径的迭代次数,加快收敛速度,增加规划轨迹的平滑度,证明方法在路径规划问题求解上的实用性。
4 结论
本文中使用强化学习对蚁群算法进行智能参数学习,以改善传统蚁群算法参数选择过程随机性强且依赖经验值的问题,并通过人工势场算法的局部优化机制,对算法的避障能力和局部优化性能作进一步改善。结果显示:
1) 该方法能针对具体环境,智能挑选出较优的参数配置,摆脱了传统蚁群算法对经验参数值的依赖,也因此降低了迭代过程因随机选择而产生的试错成本,最终以更少的迭代次数和更快的收敛速度搜索到最优路径。
2) 在不同维度的障碍物环境中,所改进的算法能在与障碍物无碰撞的前提下,较快收敛到最短路径。
3) 面对高维复杂障碍物环境中的最优路径问题,改进的蚁群算法收敛速度大幅提升,且迭代次数明显减少,最优路径拐点数减少20%以上,规划路径更加平滑。
本文中对蚁群算法的改进过程展现了较好的应用前景和价值。基于本文中的研究,作者将进一步推进对多组参数以及耦合参数的组合优化问题的研究。

