无人机辅助移动边缘计算中的任务卸载算法

李校林，江雨桑*

（1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 通信新技术应用研究中心，重庆 400065）

0 引言

为了满足用户多样化的需求，越来越多的物联网设备被部署到网络中，大量设备接入无线网络并且依靠在线资源处理各种任务。通过核心网络卸载大量任务，并在中央云服务器上处理会造成网络流量拥塞，增加延迟。移动边缘计算（Mobile Edge Computing，MEC）［1］的出现缓解了这些问题，它可以将云计算资源和服务迁移到离终端更近的地方，从而有效降低通信延迟和能耗。

MEC 网络中，根据应用场景［2］，通常采用两种卸载模式：部分卸载模式和二进制计算模式。部分卸载模式是计算任务被分为几个部分，其中一部分在本地计算，其他部分则通过卸载到MEC 服务器来计算。在对计算要求较高的场景中，计算量较低部分可以本地计算，计算量较高部分可以卸载计算。对于二进制卸载模式，计算任务在本地计算或一起卸载计算。例如，在进行信道状态信息估计时，为确保估计精度［3］，必须将收集到的原始数据样本作为一个整体进行计算。

虽然MEC 有许多优点，但在现有工作中，MEC 服务器的部署是固定的［4-5］，随时随地部署MEC 服务器具有挑战性。固定基础设施提供的MEC 服务在通信设施稀疏或发生突发性自然灾害的情况下无法有效工作。由于无人机（Unmanned Aerial Vehicle，UAV）灵活机动、易于部署、可快速响应，UAV 辅助MEC［6］系统被引入作为移动用户的计算服务器。通过在UAV 上的MEC 服务器提供额外的计算资源，能加快终端设备的计算，避免移动用户频繁与云通信或将任务上传到云，从而缓解通信拥塞的问题。但UAV 辅助MEC系统仍存在许多挑战：如何选择适当的终端设备调度来最小化所有终端的计算时延；如何在存在环境障碍（树木或建筑物）的情况下动态选择合适的通信链路；如何实时控制UAV轨迹。因此，动态选择合适的通信链路和实时决策任务卸载比、控制UAV 轨迹在UAV 辅助MEC 系统中非常重要。本文的主要工作包括以下三方面：

1）考虑存在障碍物遮挡情况下的UAV 辅助MEC 系统，建立动态信道下的任务卸载问题模型。在能量约束条件下，以最小化最大处理时延为目标，通过联合优化终端设备调度、UAV 轨迹和任务卸载比求解。

2）针对上述任务卸载问题，设计了相应的马尔可夫决策过程（Markov Decision Process，MDP），提出一种基于双延迟深度确定性策略梯度（Twin Delayed Deep Deterministic policy gradient，TD3）的时延最小化任务卸载算法（TD3 based Task Offloading Algorithm for Delay Minimization，TD3-TOADM）。该算法将MDP 元组作为训练样本，在动态信道条件下，实时控制UAV 轨迹和选择最优任务卸载比。

3）仿真实验表明，在不同参数和通信条件下，本文算法的表现均优于基于演员-评论家（Actor-Critic，AC）的任务卸载算法、基于深度Q 网络（Deep Q-Network，DQN）的任务卸载算法和基于深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）的任务卸载算法。

1 相关工作

现在的很多研究工作是关于UAV 辅助MEC 中的计算卸载［7］和轨迹控制［8］的。我们根据所提方法及其研究目标将UAV 辅助MEC 文献分为以下几种类型：

1）最小化整个系统或移动用户的能耗。Xiong 等［9］为了减少推进能量，提出UAV 只在特定时间或特定位置提供卸载计算服务。这种方案未有效发挥UAV 灵活机动、易于部署的优势。Wang 等［10］为了延长UAV 的运行时间和相关网络寿命，通过联合区域划分和UAV 轨迹调度来最小化UAV的总能耗；但该方案不适用于动态场景。

2）最小化任务完成时间。Hu 等［11］采用基于罚双分解和L0 范数的算法，最小化总处理时间，包括传输时间、计算时间和局部计算时间。嵇介曲等［12］提出一种惩罚凹凸过程的算法，求解所有用户的最大时延总和最小问题；但未考虑实际应用中存在障碍物阻挡的情况。

3）权衡能耗和时延。Zhan 等［13］通过联合设计UAV 的弹道、完成时间和卸载计算实现了系统的资源分配，最大限度地减少UAV 的能耗和完成时间。Zhang 等［14］考虑随机用户数据到达，在队列稳定和UAV 轨迹约束下最小化长期平均加权和系统能量；但是该方法中的地面用户是静态的，在每个时隙中重新计算了从初始位置到目的地的整个轨迹，增加了计算复杂度。近几年联合优化方法被学者广泛研究，由于UAV 的机载能量有限，联合优化方法的能量消耗和计算速度均过 于苛刻。Chen 等［15］利用深 度强化学习（Deep Reinforcement Learning，DRL）方法控制卸载决策，以提高感知延迟的满意度和移动用户的能源消耗。

上述文献中，大多数使用的UAV-地面信道模型遵循自由空间路径损耗模型链路的确定性视距（Line Of Sight，LoS）信道，这在城市或郊区环境中并不准确。其次，UAV 辅助通信系统中通信条件是时变的，任务卸载问题大多非凸性强，传统优化算法难以有效解决。最后，广泛用于学习和优化UAV 辅助MEC 系统各种问题的机器学习算法［16］需要提前提供足够的数据样本，对于决策问题是不现实的。相比之下，DRL 由于其本质特征，即从现实环境动态学习采集数据样本，已经成为解决这一决策问题的有效解决方案。基于上述分析，本文在一个由一架UAV 和多个终端设备组成的UAV辅助MEC 系统的场景下，考虑环境障碍的阻塞、通信条件时变和能量等约束，将非凸任务卸载优化问题定义为MDP 问题，考虑到高维连续动作空间，利用基于双延迟深度确定性策略梯度的任务卸载算法TD3-TOADM 联合优化终端设备调度、UAV 轨迹和任务卸载比使计算时延最小化。

2 系统模型

2.1 通信模型

本文考虑一个由M个终端设备和单个UAV 组成的UAV辅助MEC 系统，如图1 所示。安装有纳米MEC 服务器的UAV 为所有终端设备提供计算和通信服务，终端设备的计算能力有限，每个终端设备卸载部分任务到UAV 计算，剩余任务在本地执行。整个任务卸载过程中产生的时延由终端本地计算时延传输时延和UAV 计算时延组成。

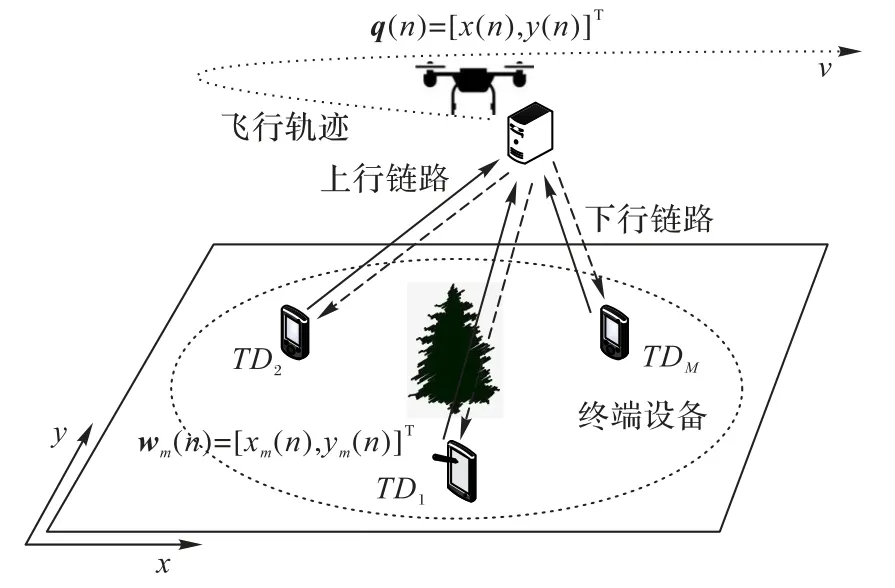
图1 无人机辅助MEC系统的模型Fig.1 Model of UAV-assisted MEC system

UAV 以时分方式向所有终端提供计算服务，整个通信周期T等步长地划分为N个时隙。假设UAV 和终端设备只能在给定区域内移动，每个时隙内，UAV 在一个固定的位置悬停，然后与其中一个终端建立通信。用二进制指标αm(n) ∈{0，1}来表示UAV 是否为终端提供服务，当UAV 在时隙n为终端提供服务时，αm(n)=1，否则为0。一个时隙内UAV 只能为一个终端提供服务，因此，终端设备调度约束为：

终端设备在该区域内低速随机移动，在笛卡尔三维坐标系中，时隙n∈{1，2，…，N}时，终端m∈{1，2，…，M}的坐标表示为wm(n)=[xm(n)，ym(n)]T。UAV 保持在固定高度H飞行时，投影在水平面上的坐标为q(n)=[x(n)，y(n)]T，UAV 飞行到新的悬停位置后更新坐标为q(n+1)=[x(n+1)，y(n+1)]T。在每个时隙，UAV 的移动性策略［17］可以表示为：

其中：v(n) ∈[0，vmax]表示飞行速度；tfly是固定的UAV 飞行时间；θ(n) ∈[0，2π]表示UAV 在x-y平面相对于x轴的水平方向。除此之外，UAV 飞行消耗的能量［11］表示为：

其中G表示飞机的载荷。

在UAV 辅助MEC 系统中，UAV 和终端设备之间的通信链路由视距信道主导，信道建模采用了自由空间路径损耗模型。假设UAV 与终端通信时为准静态场景，终端和UAV 在计算卸载期间保持不变。则在时隙n时UAV 和终端m的平均信道增益［12］可以建模为：

其中：β表示参考距离1 m 时的信道增益；dm(n)表示终端m与UAV 的欧氏距离；H表示UAV 的飞行高度。

考虑到UAV 和终端之间可能会有障碍物的阻挡，终端m在时隙n时的无线传输速率可以表示为：

其中：B表示传输带宽；σ2表示高斯白噪声功率；P表示终端在上行链路的传输功率；pNLOS表示非视距条件下的传输损耗；bm(n)表示在时隙n时UAV 与终端m之间是否有障碍物阻挡（bm(n)为1 表示有阻挡，为0 表示无阻挡）。

研究中常用无线传输速率公式可参考文献［18］。考虑到实际应用中存在阻碍物遮挡产生传输损耗的可能，本文使用文献［19］中的微波技术，将非视距条件下的传输损耗添加到公式中表示障碍物对UAV 通信的影响。当UAV 和被服务终端有阻挡时会产生传输损耗，传输速率下降，无阻挡时与常用公式相同。

2.2 计算模型

本文中的UAV 辅助MEC 系统采用部分卸载模式，定义cm(n)为终端m在时隙n卸载到UAV 上的计算任务比例，1 -cm(n)为在本地计算的任务比例。

1）本地计算。

计算任务在终端本地执行时，终端m在时隙n的本地执行时延表示为：

其中：Dm(n)表示终端m计算任务的大小；C表示处理1 bit 任务所需的CPU 周期；fm表示终端m的计算能力，单位是每秒CPU 的圈数。

2）卸载到UAV 计算。

由于MEC 服务器处理后的计算结果非常小，可以忽略不计，所以本文不考虑下行链路的发送延迟。UAV 服务器的处理时延可分为两部分，首先是终端m在时隙n将任务卸载到UAV 的传输时延，可表示为：

其次是服务器计算产生的时延，表达式如式（10）：

其中：fUAV表示UAV 的计算能力。此时UAV 计算任务产生的能量消耗为：

其中：κ为芯片结构对CPU 处理的影响因子，κ=10-27。

2.3 问题建模

在本文提出的UAV 辅助MEC 系统中，目的是在离散变量和能量消耗的约束下，联合优化终端设备调度、UAV 轨迹和任务卸载比，以最小化所有终端的最大时延之和。综上，优化问题建模为：

其中：E表示UAV 电池容量；式（13）～（14）是约束终端和UAV 只能在给定区域移动；式（15）表示无线信道中的阻塞情况；式（16）表示任务卸载比；式（17）～（18）是保证调度一个设备在时隙n进行计算；式（19）是指UAV 要在整个通信周期完成所有计算任务；式（20）是确保UAV 飞行和卸载计算在所有时隙消耗的能量不超过最大电池容量。

3 算法设计

上述优化问题是一个混合整数非凸性问题，并且，在所考虑的场景中，系统状态的复杂性高，计算任务卸载决策需要连续动作空间的支持。采用传统的优化方法难以解决上述问题。DRL 已被证明是处理高维连续空间［20］复杂控制问题的有效方法。因此，本章提出一个基于DRL 的方案解决优化问题。强化学习（Reinforcement Learning，RL）是一种具有自学习能力并能做出最佳决策的算法，它考虑了agent 与其环境之间交互的例子，旨在学习最大化回报的策略。RL可以用来解决定义为四元组(S，A，P，R)的MDP 问题，其中：S为状态空间，A为动作空间，P为状态转移概率，R为奖励函数。每时隙在给定状态s∈S的情况下，agent 选择与其策略π：S→P(A)相关的行动a∈A，并获得奖励r∈R。MDP 的目标是找到一个能够最大化预期累积收益Rn=表示折扣因子）的最优策略。DRL可以被认为是RL 的“深度”版，它使用多个深度神经网络（Deep Neural Network，DNN）作 为Q 值函数Q(s，a)=E[(Rn|s，a)]的逼近器，Q(s，a)是在状态s中执行操作a时的预期收益。

3.1 构建MDP

为了能够应用DRL 方法解决优化问题，本文将原问题重新表述为MDP 结构。UAV 辅助MEC 系统中计算卸载问题的状态、行为和奖励如下：

1）状态空间。在本文的UAV 辅助MEC 系统中，状态空间由M个终端、UAV 及其环境共同确定。时隙n时状态空间表示为sn={W(n)，bm(n)，q(n)，D(n)，Dr(n)，Er(n)}，其 中：W(n)={w1(n)，w2(n)，…，wM(n)}表示被UAV 服务的终端m的位置；q(n) 表 示UAV 的位置；bm(n)={b1(n)，b2(n)，…，bM(n)}表示终端m的信号是否被障碍物阻挡；D(n)={D1(n)，D2(n)，…，DM(n)}表示终端m随机生成的任务大小；Dr(n)表示系统在整个时间段内需要完成的剩余任务的大小；Er(n)表示UAV 剩余的电量。

2）动作空间。agent 根据系统当前状态和观察到的环境，选择待服务的终端m、时隙n时任务卸载比、UAV 飞行角和UAV 飞行速度。因此，系统动作集可以表示为：an={m(n)，cm(n)，v(n)，θ(n)}，其中：m(n) ∈[0，k]表示终端设备调度的 动作变 量，如 果m(n)=0，m=1；m(n) ≠0，m=是向上取整符号。在连续的动作空间内，UAV 的飞行角度、飞行速度和任务卸载比能够被精确优化。通过联合优化动作空间内的4 个变量，系统计算卸载的时延能最小化。

3）奖励函数。本文目标是在保证能量消耗的前提下，最大限度地降低任务计算卸载的时延。因此，每个动作的目的是最小化最大计算时延，系统奖励应该与最大计算时延负相关，其定义为：

当执行动作an后，计算时延越小获得的奖励越大，就越会向期望的方向发展。

3.2 基于TD3的任务卸载算法

根据3.1 节构建的MDP 问题，考虑到任务卸载优化问题的高维连续动作空间，提出基于TD3［20］的任务卸载算法TD3-TOADM，如图2 所示。TD3 算法包括一个权重为φ的Actor网络和两个权重为θ1和θ2的Critic 网络，这两个Citict 网络可以解决Q 值的高估问题，获得更好的学习效果。因此，TD3算法能更稳定地求解本文的优化问题。此外，为提高学习稳定性，TD3 采用了权重为φ′的Actor target 网络和权重为和的Critic target 网络。

图2 TD3-TOADM网络框架Fig.2 TD3-TOADM algorithm network framework

算法1 总结了解决任务卸载优化问题的TD3-TOADM，该DRL 算法不需要提前提供足够的数据样本。算法具体流程如下：首先，初始化6 个神经网络的权重参数和经验缓存。在每一回合（对优化问题的一次求解），UAV 根据Actor online网络πφ(s)和随机噪声ε选择行动。UAV 执行动作后将获得奖励rn和下一个状态sn+1以及状态转移样本(sn，an，sn+1，rn)。为了稳定训练过程并提高样本效率，UAV 将状态转移信息(sn，an，sn+1，rn)存储在经验缓存区R中作为训练online 网络的数据集，然后从经验缓存中随机抽取大小为Bs的状态转移信息数据(sj，aj，，rj)作为Actor online 网络、Critic online 网络的一个小批量训练数据。当经验缓存已满时，算法采用以下的方式来更新经验缓存：首先找出经验缓存中奖励值最小的状态转移信息数据，若该数据的奖励值小于新数据的奖励值，则用新数据替代这个数据；否则新数据替代经验缓存中最旧的数据。通过将sj输入Actor online 网络生成策略πφ(sj)，UAV 可以使用策略梯度法更新Actor online 网络的权重：

此外，为防止在Q值的窄峰上过度拟合，将随机噪声ε添加到Actor target 网络中，这样可以实现更平滑的状态动作值估计。修改后的目标动作如下：

然后可以获得目标动作值：

根据策略πφ(sj)，两个Critic target 网络将通过最小化损失函数L(θi)执行梯度下降来更新权重θi，同时获得两个Q 值Qθ1(sj，πφ(sj))和Qθ2(sj，πφ(sj))。L(θi)定义为：

接下来，根据式（22）和（25），UAV 可以使用以下等式更新3 个online 网络的权重：

其中：αa和αc为学习率，UAV 每d个时隙更新Actor online网络。

最后，为了稳定训练过程，通过复制相应online 网络的权重，UAV 根据式（27）～（28）更新3 个target 网络的权重：

其中：τ为软更新系数。

算法1 基于TD3 的任务卸载算法TD3-TOADM。

用式（26）更新Actor online网络。

根据式（28）更新3个target网络的权重。

4 仿真实验和结果分析

4.1 仿真环境以及参数设置

仿真实验使用Python3.7 和TensorFlow1 框架在Anaconda 平台上模拟系统环境，设置了1 个UAV 和4 个地面终端设备随机分布在一个100 m × 100 m 正方形区域的模型，对UAV 轨迹、终端设备调度和任务卸载方案进行仿真，实现了TD3-TOADM 任务卸载算法。仿真中的其他参数主要参考文献［12］，如表1 所示。

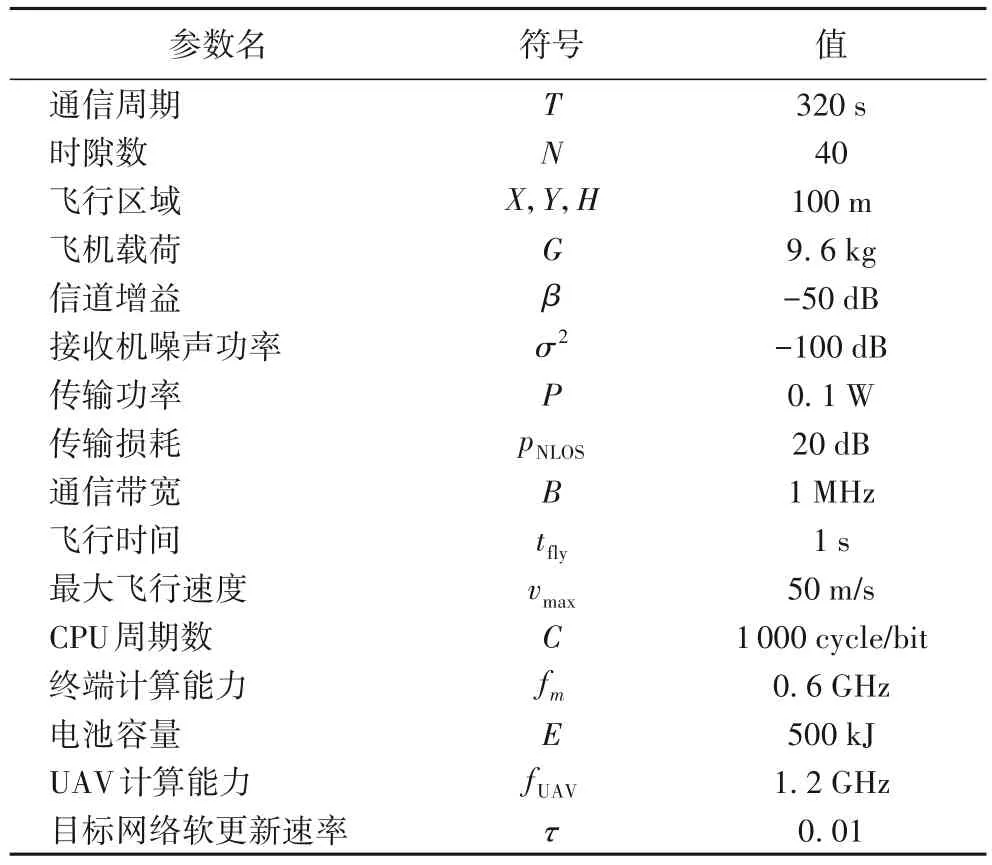
表1 主要参数设置Tab.1 Main parameter setting

4.2 结果分析

首先对算法中重要的超参数折扣因子γ进行分析，γ取适当的值将提高训练后策略的最终性能。为确定γ值，设算法网络参数学习率αa=0.001，αc=0.002，经验缓存大小为104，批学习大小Bs为64。γ分别取0.001、0.5 和0.9，它对算法性能的影响如图3 所示。结果表明，γ=0.001 时，计算卸载策略性能最佳、时延最小，故本文实验将γ设置为0.001。

图4 展示了UAV 在任务大小为100 Mb 和60 Mb 情况下的卸载轨迹。为了反映UAV 位置变化对计算时延的影响，每个时隙对轨迹进行采样绘制UAV 轨迹，可以观察到，随着任务大小的增加，UAV 飞得更靠近距离远的终端，从而有助于建立高质量的链路，进一步减少卸载时间。

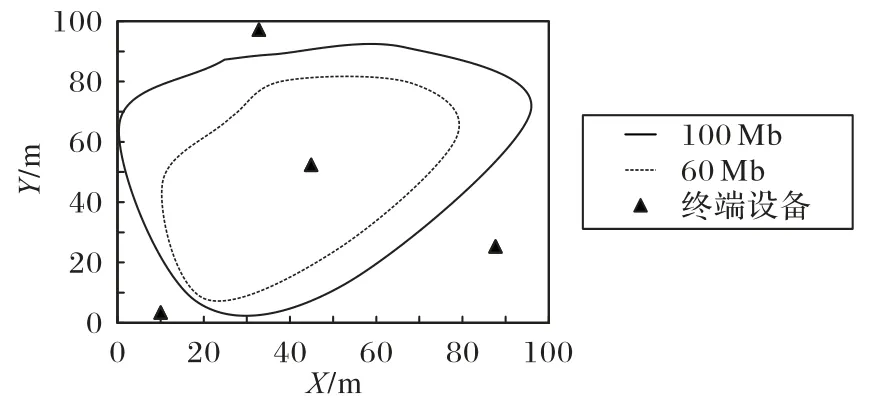
图4 任务大小不同时的UAV轨迹Fig.4 Trajectory of UAV with different task sizes

为验证TD3-TOADM 的有效性和优越性，本文选取3 种任务卸载算法在相同的应用场景下进行仿真对比：第一种是基于AC 的任务卸载算法，它可以解决连续动作空间问题；第二种是基于DQN 的任务卸载算法，这是传统的基于离散动作空间的DRL 算法；第三种是基于DDPG 的任务卸载算法，该算法是近年各类研究中经常使用的先进DRL 算法。图5展示了计算任务大小为100 Mb 时，不同算法下时延随训练次数变化的情况。从图中可以看出，随着迭代次数的增加，AC 算法难以收敛，而DQN 算法、DDPG 算法和TD3-TOADM都可以收敛。因为AC 算法存在着Actor 网络和Critic 网络同时更新的问题，在某些情况下可能不收敛。而其他3 种算法有双网络结构（评价网络和目标网络），能找到最优的行动策略后收敛。在各算法收敛后，TD3-TOADM 得到的时延为59.59，DDPG 算法得到的时延为64.93，DQN 算法得到的时延为92.33，TD3-TOADM 得到的计算时延减小了8.2%以上。

图5 不同算法的收敛性对比Fig.5 Comparison of convergence of different algorithms

在满足UAV 电池容量约束下，本文将AC 算法、DQN 算法、DDPG 算法、TD3-TOADM 得到的计算卸载时延作为评价标准。图6 展示了各算法在不同任务大小、终端数量和飞行时间下的计算时延。由图6 可知，对于相同的任务大小、终端数量和飞行时间，TD3-TOADM 的时延在4 种算法中始终最低。以图6（a）为例，当任务大小为60 Mb 时，DDPG 算法的时延为39，DQN 的时延为73，TD3-TOADM 的计算时延减小了23%以上。随着终端数和飞行时间的增加，AC 算法和DQN 算法的时延波动较大，DDPG 算法波动较小，TD3-TOADM 趋于平稳。这是因为DQN 算法输出动作取值范围差异较大。因此，当样本作为训练DNN 的输入时，DNN可能倾向于输出更大的值。DDPG 算法和TD3-TOADM 的Actor 网络输出多维动作，能确保DNN 的输入数据都在［0，1］范围内，保证其收敛性和稳定性。

为研究终端计算能力对系统进行卸载任务的影响，图7分别测试了在不同终端计算能力（fm)下，TD3-TOADM 计算卸载产生的时延和任务卸载比。可以发现，终端计算能力较小时，本文优化方案优化后的处理延迟要高于终端计算能力较高时的处理时延。另一方面，从图7（b）中能看出当终端的计算能力较大时，系统的平均任务卸载比较小，终端更倾向于在本地执行任务。终端计算能力越小，系统的数据处理越慢，导致本地执行和卸载之间的最大时延越大。这说明任务卸载比是对连续动作控制系统延迟影响较大的因子。

图7 TD3-TOADM的终端计算能力对比Fig.7 Comparison of terminal computing power of TD3-TOADM

上述实验对比结果表明，本文TD3-TOADM 的表现均优于对比的3 种卸载算法，具有较好的收敛性和鲁棒性。因此，TD3-TOADM 能够联合优化终端设备调度、UAV 轨迹和任务卸载比后得到相对较小的最大处理时延。

5 结语

本文研究了在一个通信周期内，同时服务于多个用户的UAV 辅助MEC 系统中的任务卸载问题。为解决计算任务卸载产生的时延过大的问题，提出一种基于DRL 的任务卸载算法TD3-TOADM 学习和优化计算任务卸载。该算法以计算任务大小、终端和UAV 位置等为输入，在电池容量等约束下，连续自适应学习调整计算卸载策略，对多个目标进行优化，通过联合优化终端设备调度、UAV 轨迹和任务卸载比以最小化计算时延。仿真实验结果表明，本文的TD3-TOADM任务卸载算法在处理时延方面有较好的性能。在未来的研究中，将会考虑多UAV 等复杂场景下的MEC 任务卸载问题。