面向业务需求的算法路径自组配模型

刘 耀，童 昕，陈一风

（1.中国科学技术信息研究所 信息技术支持中心，北京 100038；2.北京大学 软件与微电子学院，北京 102600）

0 引言

本文立足于情报工作常用算法及相关算法平台，数据集为项目中累积的面向业务的所有算法以及依据算法源代码拆分后的算法代码组件，这些算法及组件来源于基于业务划定的算法范围所构建的算法资源库。本文选择基于Python代码实现，面向业务中涉及的机器学习算法进行代码解析与组配研究，从而实现智能化算法管理平台中的算法结构化及算法业务流自组织。本文的主要工作包括3 个方面：

1）代码组件表示方法建模。本文在综合研究抽象语法树、控制流程图等代码结构提取方法的基础上，提出一套对逻辑结构、数据流以及组件间的调用关系进行综合解析的方法，并通过基于图卷积网络（Graph Convolutional Network，GCN）对代码组件进行图向量表示。

2）提出了代码路径自组配模型。本文提出使用聚类的方法进行算法代码的功能挖掘，发现算法代码间的路径关系，并基于排序实现算法路径自组织。

3）通过实验验证了对算法进行解析得到算法代码组件，并在此基础上进行算法路径自组配可行性实验及对比实验。

1 相关工作

本文旨在基于代码的结构特征与语义特征，从业务需求出发检索资源库中的代码，在算法代码的理解基础上，根据业务需求匹配得到的代码进行组配。在本文中，生成指对算法代码的复用。对算法代码复用的基础是有能力拆分完整的算法代码，拆分建立在对算法代码的理解之上。

1.1 代码复用

代码复用［1］在企业中普遍使用，开发人员出于效率、成本、代码准确性的考虑以多种形式实现代码复用，已有的研究表明恰当的代码复用可以快速集成功能、提高代码准确性。

国内外关于代码复用的研究经历了3 个阶段：1）传统代码复用阶段，开发人员从互联网手动获取可复用代码、代码文档、代码用例等，并对代码进行手动更改。2）基于数据挖掘的代码复用阶段，分为代码片段级别和代码功能模块两个维度的复用：在代码片段级别，Lin 等［2］将克隆检测结果与多段代码之间的差异比较技术相结合，检测实例间的差异，同时认为不同代码的差异点可以转化为代码可变点；而代码功能模块的复用即从相似代码块中抽取功能相似的设计和模板，开发人员在此基础上针对具体需求实现特定功能［3］。3）基于深度学习的代码复用主要用于训练和预测阶段［4］，基于传统统计学习的代码推荐方法［5-10］和基于深度学习的代码推荐方法［11-13］将代码视为序列，并将包含N元语法（N-gram）等在内的传统统计模型或长短期记忆（Long Short-Term Memory，LSTM）人工神经网络在内的深度学习模型用于学习和训练，但这些研究方法缺乏对代码的结构信息的考量，导致它们无法有效捕获远距离代码间关系，同时并未实例化代码中的参数。为了改进这一情况，基于Tree-LSTM（Treebased LSTM）的推荐方法DeepAPIRec［14］应运而生，通过训练语句模型预测抽象代码语句，并构造参数模型以实现代码语句的实例化。

基于此，本文确定了将算法代码块进行拆分可以实现复用这一思想，将算法代码进行结构化处理，同时获取代码的语义信息，为代码复用作准备。

1.2 代码理解

为了实现代码理解，研究界通常采用强化学习和随机编译进行超优化［15-16］，或者借用自然语言处理（Natural Language Processing，NLP）中的概念处理人工编写的代码。这一方式的理论基于软件语料库具有与自然语言语料库相似的统计特性，这些特性可以用来构建更好的软件工程工具［17］。在代码字符（token）的上下文表示中，主流方法之一依赖于词典编纂位置［11］；另一种方法则是挖掘代码的结构，使用数据流图［18］、控制流图（Control Flow Graph，CFG）［19-21］、抽象语法树（Abstract Syntax Tree，AST）［22］、AST 中的路径或扩展的AST［23］，例如使用连接不同用途和对应于变量［18］的语法令牌的更新的附加边。AST 是指一种用于表达源码抽象语法结构的树状结构［24］，Zettlemoyer 等［25］将AST 视作组合范畴语法（Combinatory Categorial Grammar，CCG）的轻量级版本，用来描绘代码结构。

算法代码作为机器语言，包含严格的结构信息，同时作为可理解的自然语言，具备语义信息。充分表达代码的结构和语义信息是进行代码解析的基础。以信息检索（Information Retrieval，IR）为代表的传统方法通常将代码片段视为自然语言文本，并基于标签对其进行建模。Kamiya等［26］和Sajnani 等［27］用标签序列或一系列标签表达代码，并将之用于代码克隆检测。另外，潜在语义标引（Latent Semantic Indexing，LSI）［28］和文档主题生成模型LDA（Latent Dirichlet Allocation）［29］也被应用于分析源码，并取得一定的效果［30-31］。但这些方法忽略了代码具有更丰富明确的结构信息，无法视为纯自然语言或者基于代码token 的方式进行处理［32］。

2 面向业务的算法路径自组配模型

本文通过将算法代码拆分为功能完整的可复用组件，以算法组件为基准构建算法代码资源库，并面向业务需求对算法组件进行检索、选择与自动组配，进而构建对应业务需求的算法代码流程。面向业务的算法自组配的起点为面向业务描述的算法代码检索。通过自然语言描述的业务信息，首先需要从算法库中找到与业务需求最符合的代码组件集合；然后从这些组件中挖掘功能集合作为待构建的算法路径的步骤，并依据先验知识训练得到的路径发现与自组织模型；最后从面向业务的算法代码组件集合中，构建面向业务的算法自组配模型的流程，如图1所示。

图1 面向业务的算法自组配模型的流程Fig.1 Flow of algorithm path self-assembling model

算法组配包括两种场景，简单需求直接匹配单一代码块，即输入需求已被拆分为算法代码步骤的最小颗粒度，进行排序重组即可。复杂需求表现为输入需求颗粒度比现有算法代码颗粒度大。此场景的处理机制是输入需求，以需求为关键词检索代码资源库中所有相关包含结构信息的代码组件，随后将检索到的代码组件聚类，判断该需求所需步骤以及步骤间的顺序，即每一需求内部形成小型组配任务。该场景需要实现两层组配，第一层是外层需求代码间的组配，该层组配与简单需求一致；第二层组配是单一需求拆分后的内部代码的组配，两层组配完成后，才能最终实现代码的可运行。

2.1 算法组件表示模型

2.1.1 代码结构提取

在对算法代码按照业务需求进行组配前，首先需要拆分算法代码，拆分后的算法代码块应为一个算法代码组件。一个组件通常包含了一个完整的功能，并且是组成算法的最小可复用单元。所谓最小，即拆分出来的代码块有且仅能实现单一步骤；所谓可复用，即拆分后的代码块需要具备一定的功能属性，能实现具体的步骤，可以在其他代码组合中运行。

通过分析算法本身的业务流程，可以将算法划分为一系列实现不同功能的步骤，每一个实现功能的步骤则可以被拆分为一个算法组件。本文面向的算法代码为Python 语言，在Python 程序设计中，函数的设计一般满足如上需求，因此对于算法组件的拆分，以函数为单位进行。

本文结合AST 中详细的变量之间赋值与操作关系，对代码中隐含的数据流程的结构进行解析，并将解析所得到的数据流程结构与CFG 中基于流程控制的逻辑控制流程相结合，得到结合数据与流程的算法代码结构。本文构建代码的结构的步骤如下：

1）对当前项目中的所有算法组件，分析它们的调用关系，并标注有调用关系的语句。

2）对代码的抽象语法树进行解析，得到树结构GAST，初始化代码结构图G。

3）基于解析出的抽象语法树，遍历其中的节点V。

4）对于逻辑结构和数据结构，分别构建逻辑控制流程节点集｛vif，vfor，vwhile，vbreak，vcontinue，vreturn｝、数据流程节点集｛vassign，vop，vcall｝和对应的数据节点集。

5）对于当前节点，如果它属于某个节点集，则将它加入结构G，如果它属于逻辑控制流程开始的节点集或数据流程节点集，则将它作为当前子树的顶点，递归构建逻辑结构与数据结构。

6）遍历完成GAST后，对返回的图，遍历其中的节点，将有组件间调用关系的节点进行连接，获得组件间调用的关系结构，最终获得代码的结构图G。

本文从算法代码库中选取代码对上述步骤进行说明，选取代码为word2vec 算法中的word2vec-run 函数代码组件。本文进行分析并构建对应的结构。在构建逻辑流程结构与数据流结构的基础上，基于对算法package 内算法组件之间调用关系的分析［33］，进一步从代码中挖掘隐性结构。基于本节提出的结构解析的步骤，对word2vec 的算法组件结构进行解析，最终共得到共37 条边，35 个节点。对所构建的结构进行可视化，如图2 所示。

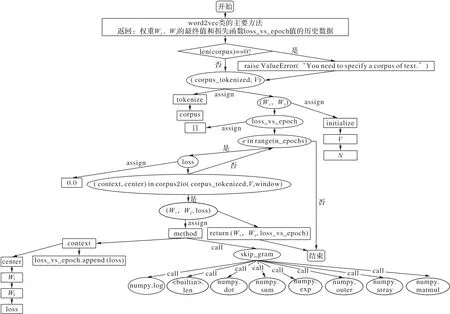
图2 word2vec算法组件结构的可视化Fig.2 Visualization of component structure of word2vec algorithm

可见，在基于CFG 对算法的隐含逻辑结构进行表示的基础上，本节提出的结构解析方法能够更加详细地对算法组件中的变量等节点进行建模，能够更加有效地挖掘与表示代码的结构。

与AST 过于详细、复杂的结构相比，本文方法更加简洁，能够从代码的显性结构中，对隐含结构进行提取；与基于CFG 的简略结构相比，本文方法更加详尽，对CFG 中未解析的流程语句中所包含的丰富结构信息进行了挖掘，能在逻辑结构的基础上添加更多有效信息，从而更加完备地对代码的结构进行表达。在数据与控制流程的基础上，进一步对算法组件间函数的调用关系进行分析，从而对组件间的依赖进行建模，更加有效地挖掘代码中的隐性结构。

2.1.2 代码组件表示

本文通过2.1.1 节步骤，实现了对代码结构的解析。在此基础上，使用GCN 以及结构中节点的word2vec 表示为输入对代码的结构与序列特征同时进行建模。本文所采用的代码数据为拆分后的算法代码库中的所有算法代码组件，共计424 个代码组件，具体步骤如下。

1）对于所有的代码组件，提取其结构与相应节点的文本序列，并根据逻辑控制流程、数据流程等对节点划分类型。

2）将提取出的结构、文本序列与节点类型序列化为JavaScript 对象简谱（JavaScript Object Notation，JSON）文件存储。

3）初始化GCN 模型，读取结构文件并构建数据集。

4）使用节点分类作为向量表示的训练任务，根据节点在代码组件中的类型，训练模型预测节点的类型。

5）训练结束后，输出模型最后一层的隐向量作为节点的向量表示。

基于以上步骤所构建的数据集统计结果如表1 所示。

表1 算法组件结构构建结果Tab.1 Results of algorithm component structure construction

基于输入的算法组件对，模型首先从中分别提取算法组件的结构信息，进而获得组件结构的图表示。其中，图表示基于GCN，所获得的表示为以图中节点为单位的向量。在下一阶段中，模型基于组件之间整体的结构与语义信息进行计算，因此，本文进一步使用注意力池化（Attention Pooling）的方法将图结构中节点的向量编码表示为整体的图编码。

最常用的基于单位向量得到整体表示的方法为对所有的单位向量进行平均。在图表示中，常用的平均方法为基于图中节点度的加权平均方法：

其中：un为节点n的向量表示，wn为基于节点度的重要性度量权重。然而，在代码的结构图中，节点的度信息无法很好地给出节点在图中的重要性，基于度的加权方法无法很好地对代码的整体结构信息进行表示。为了在图结构的整体编码中强调图中更重要的节点，通常使用注意力机制（Attention Mechanism）为图中节点增加可学习的权重，从而对基于节点对路径关系的重要性对其向量进行加权表示。

注意力机制在图像处理与自然语言模型中被广泛使用，并取得了广泛的成功。在自然语言模型［34］中，通过在全连接网络中使用注意力机制，模型可以对长距离依赖进行有效建模，同时避免了梯度问题与模型复杂度问题。在图结构中，对于节点向量编码U∈RN×D，本文在模型中增加权重参数矩阵W∈RD×D作为注意力权重，并通过注意力权重加权的节点向量与图结构向量之间的内积作为最终的注意力得分，用于计算整体的图结构信息。最终基于注意力的算法组件表示如式（2）所示：

其中：fnorm为归一化函数，用于对最终的注意力得分进行归一化；f1为非线性变换函数；最终得到的VG为整体的图结构表示。

使用基于注意力的加权表示，模型分别对输入的算法组件对进行结构与语义信息的向量表示，并使用向量表示作进一步的路径计算。

2.1.3 组件对融合向量表示

模型通过计算图结构之间的关系判断组件之间是否存在路径，其中组件结构信息的交互通过卷积计算进行。为了对结构之间的关系进行计算，本文借鉴ConvE（Convolutional two-dimensional knowledge graph Embeddings）［35］中获得的知识图谱三元组中实体与关系的二维向量表示，使用卷积网络获得两个算法组件结构的融合向量，从而在基于目标使用反向传播进行优化时，将路径信息通过卷积网络获得的融合向量分别传播到各个组件的表示中，从而使得模型能够同时利用输入的算法组件中的结构信息并根据组件间的结构信息的交互计算判断算法组件之间是否存在路径。其中，输入的算法组件的向量融合表示如式（3）所示：

通过将组件对的结构表示进行卷积计算，模型得到了组件结构之间的融合向量，并以此为依据进行结构间关系的计算。

2.2 基于语义扩充的检索模型

本文面向的对象主要为较为笼统的自然语言描述的业务需求。为了对自然语言中的检索词进行语义扩展，基于算法相关资源构建概念共现网络。算法文档和相关论文中包含的概念都可用于描述算法组件，因此将算法相关文档、论文中的概念提取出来构建概念网络。首先，在代码库的基础上，构建与之关联的文档库和论文库，用于代码组件检索时进行语义扩充；然后，使用多语言BERT（Multilingual Bidirectional Encoder Representation from Transformers，M-BERT）在中英两种语言上进行序列标注任务，从而识别中英文论文中的概念；最后，利用提取出的概念实体进行面向业务的代码检索模型构建。

本文基于所构建的代码表示模型，将算法代码库中的所有代码进行向量化表示，并提取业务需求中的概念进行向量化，通过向量检索的方式，从结构与语义的层面对代码进行深度检索，实现面向业务的算法代码获取。本文构建的检索模型的步骤如下。

1）给定业务需求，使用构建的概念识别模型，从中提取概念关键词。

2）在概念抽取的基础上进行分词并过滤停用词，获得业务需求的词袋表示。

3）基于拆分后的算法代码组件，对于每个组件，提取其中的方法调用的变量名称，将同一组件内的变量视为有共现关系，并提取与之关联的算法文档、论文中的概念，基于窗口构建概念的共现关系。遍历所有组件，构建共现矩阵C。

4）基于业务需求提取出的概念，从共现矩阵中检索概念与变量名称的共现，得到共现矩阵C'中矩阵的元素为概念与变量共现的次数。

5）对于业务需求中的概念i，从C′取与它共现次数最高的前e个词作为业务需求的扩充概念，将它加入业务需求的词袋表示，其中e的取值由阈值决定。

6）基于业务需求的词袋表示，获得它基于词袋的向量表示；使用该表示对算法代码组件库中所有组件的向量表示进行检索。其中，检索的分值由式（4）给出：

其中：xq为业务需求的向量表示，xj为算法组件j的向量表示，常量ε作为约束值。

2.3 路径关系发现模型

将通过2.1.3 节方法得到的融合向量使用全连接网络输出，并基于全连接网络的输入与目标之间计算误差，从而对组件间的路径关系建模。将路径关系的挖掘视为二分类问题：将组件对输入模型，如果组件之间存在路径，模型应将关系预测为1；如果没有路径关系，则模型预测应接近0。然而，仅使用二分类任务对路径挖掘建模，模型难以收敛。在此基础上，本文同时将路径发现任务视为排序任务，在联合学习的框架下，同时对二分类任务与排序任务进行学习，从而对算法组件之间的路径关系进行建模。具体地，模型在阶段2 使用的二维卷积模型输出的向量基础上，使用2 层的全连接神经网络将最终的表示分别映射到排序任务的向量输出与二分类任务的向量输出。在计算排序任务时，模型随机从负例中抽样算法组件对，并认为正例的组件对在排序上得分应高于负例的得分。基于联合训练，模型的损失函数为：

基于以上联合损失，模型利用算法组件之间的结构特征，针对组件之间的路径关系进行优化。

基于上述模型内容，研究所构建的算法组件间路径发现模型如图3 所示。

图3 路径发现模型Fig.3 Path discovery model

2.4 路径自组织模型

2.3节中通过构建路径发现模型，从聚类挖掘出的功能集合中进一步构建了以算法组件对为单位的算法步骤，初步形成了算法路径。然而，在这一步中挖掘出的路径中的组件处于无序状态。为了实现算法路径的自组织，需要在构建出的路径的基础上，通过挖掘出的算法组件的结构信息与语义信息，依据所形成的路径的整体结构与语义关系，使得作为步骤的算法组件能够实现自组配，从而在路径上形成有序的算法组件路径，最终实现算法自组配。

为了让算法组件步骤能够基于结构与语义信息自组配，可以将它视为面向整体算法流程的检索任务：给定已经挖掘出的整体的无序算法路径，为路径中的算法组件给出分值，使得在组配流程中需要被组配到流程前列的算法组件得到更高的分值，而在流程中处于后列的算法组件得到更低的分值。

以上问题可以形式化为：给定从功能集合中构建出的算法组件路径子集D={d1，d2，…，dn}，构建检索函数f，应该返回一个排序r*，使得D中的算法组件的排序满足在源代码中的先验分布。基于上一节的路径发现模型所构建出的算法步骤子集，其中的算法组件以组件对的形式被发现，因此，本文基于对间（pairwise）的方式从构建出的算法路径中，进一步构建排序模型，实现算法路径的自组织。

上一节中所构建的算法组件间路径r与最佳排序r*可以视为满足弱序条件（weak ordering）的D×D上的二元关系组，其中r⊂D×D且r*⊂D×D。对于r与r*中的算法组件di与dj，如果它们顺序相同为同序对，不同则为异序对，数量分别为P和Q。在数量为n的有限算法组件子集D中，P和Q的和为则r与r*的kendall 系数定义为：

其中ra和rb用于代表两个路径。

可以看出，两个路径的kendall 系数只与Q有关，而Q给出了平均精度的下界：

因此，要构建接近最优算法路径r*的算法组件子集，则要给定这一路径的集合D作为检索q，学习一个能够最大化kendall 系数τ的函数f：

对于本节研究所面向的算法组件子集，构建出的路径以算法对(di，dj)的关系呈现，因此对于学习函数f，可以将它视为根据集合D判断组件对中哪个组件在路径中的位置更靠前，即：

其中：w是学习的权重向量；Φ(q，di)是检索式q与文档di之间的匹配关系映射所得的相关特征。函数f最大化kendell系数式，等价于最小化式中的Q，等价于学习一个w使得式中的二元组数量最大。因此，问题转化为一个二分类问题，分类器通过学习w计算式，对二元组进行真值标注。在构建针对功能集合的算法路径中，通过实验发现，在联合学习的框架下进行训练能够使得模型更稳定地收敛。因此，在上述任务的基础上，将路径中的算法组件对扩展到整条路径中的算法组件子集，对于集合D与集合中所有的算法组件，模型同时学习一个函数f(w)，从而对于集合中的算法组件dj，排在路径中最前列的概率［36］为：

因此，可以通过交叉熵损失最大化形成算法路径的概率：

其中y为最优算法路径r*中算法组件的得分序列。

基于上述研究与所构建出的算法组件组成的无序算法路径子集，在联合学习的框架下，构建了算法路径的自组织模型。模型接受3 组输入：所有组成路径的算法组件子集、待排序的算法组件1 和待排序的算法组件2。模型首先对以上的算法组件分别提取结构与序列信息，并基于注意力池化分别将输入的组件表示为能够对图的整体结构与序列信息进行编码的向量。模型进一步将所有组件子集的表示视为查询向量query，将待排序的组件1 的表示视为键向量key，根据查询向量query与键向量key，获得它的融合向量vector；基于vector与组件2 的表示，给出组件1 与组件2 在所有组件子集的语境下的相对排序；同时，基于融合向量vector，获得它在所有组件子集中的排序得分。本文基于源代码中所包含的算法组件的先验排序构建训练集对模型进行训练，从而得到算法路径自组织模型，模型如图4 所示。

图4 算法路径自组织模型Fig.4 Self-assembling model of algorithm path

3 实验与结果分析

3.1 基于功能的算法步骤挖掘

在本节中，选取词频-逆向文件频率（Term Frequency-Inverse Document Frequency，TF-IDF）相关的算法作为资源，作为进行算法自动组配实验的数据。在本文构建的算法资源库中，以TF-IDF 为关键词进行检索，检索结果为库中所有与TF-IDF 相关的算法，包括算法的源代码以及拆分后的TF-IDF 的算法代码，拆分后的算法块为有完整功能的最小可复用单元，可以作为算法组件使用。检索结果共包括5 个不同来源的TF-IDF 算法，总计25 个组件构成，数据统计如表2 所示。

表2 实验数据统计Tab.2 Experimental data statistics

基于对算法代码的向量表示，本文选取常用的聚类算法k-means 进行聚类。通过计算所有类簇数量k取值范围内的评测指标，并选取最优指标对应的类簇数量，确定所需k的取值。k是一个相对重要的参数：若k取值过低，则无法有效区分不同的算法组件，导致原本需要进行组配的两类算法组件在同一个类里，从而影响组配进行；若k取值过高，则会产生冗余的组件类型。定义k的取值范围为k∈range(5，12)。

为了确定最优k值，本文提出基于轮廓系数（Silhouette Coefficient）与方差比准则（Calinski-Harabasz score）的加权指标进行类簇数量确定的方法。该指标计算方式如下：

其中：最终的评价指标为轮廓系数与方差比准则的加权和，评价指标值越高，表明k的取值越好；权重大小根据经验确定，在实验中选取α=0.2，β=0.8。选用式（14）中提出的加权指标，对聚类模型的类簇数量进行确定。根据实验结果，在k=6 时，得到最优指标。其中k取不同值时的指标变化如图5 所示。

图5 k取不同值时的指标变化Fig.5 Influence of k on Score

从表3 聚类结果可见，大部分类簇所包含的功能均得到了有效区分。分析未能正确聚类的算法组件，所实现的功能、其中所包含的变量命名以及文档与被聚在同类的其余组件均较为相似，因此未能正确聚类。在类簇0 中，对构建字典的代码内容分析，其本质为统计语料库中不同词出现的次数并构建字典，大部分实现与计算TF 值的实现一致，因此被聚在同一类中。实验结果表明，本文提出的使用聚类模型对所有的候选代码组件进行功能区分以及步骤挖掘的方法能够较好地区分出不同功能的候选代码，且基于聚类模型制定的k值评价指标能够有效挖掘算法流程中步骤数，从而为进一步的代码组配提供依据。

表3 TF-IDF算法组件聚类结果Tab.3 Component clustering results of TF-IDF algorithm

3.2 算法路径关系发现

本文选取算法代码库中所有拆分后的代码，根据源代码中函数执行的顺序作为路径的先验知识，对算法组件之间的路径关系进行标注。同一源代码中的算法组件之间存在路径关系，本质是同一源代码的算法组件之间因为变量命名、函数调用以及输入、输出的参数等变量所构成的图结构之间存在一定先验联系。在源代码中，如果两个算法组件存在执行的先后顺序，则认为这两个组件之间存在路径关系，对于存在路径的算法组件，将这两个组件之间的关系标为1。标注完毕后，选取不同的算法源代码，不同算法之间功能不同的算法组件不存在路径关系。按照这样的策略，从所有样本中获取负例样本，数量远大于正例样本，因此，在进行训练时，根据不同算法之间功能不同的算法组件不存在路径关系这一假设，制定了抽样策略，在更新模型参数时，根据抽样策略随机抽动态样出不存在路径关系的组件对，将路径关系标为0。最终，共得到正例样本385 个。本文对样本进行随机排序，并按照4∶1 的比例从获得的正例样本中构建训练集与测试集，并根据抽样策略抽取了80 个算法组件对作为负例样本的测试集。使用算法组件先验知识得到的数据集进行训练后，使用得到的模型，进一步从3.1 节聚类挖掘出的不同功能类别的算法组件中，进行算法路径的挖掘，以进一步验证模型的有效性。

初始化上述路径发现模型使用的参数如表4。

表4 路径发现模型的初始化参数Tab.4 Initialization parameters for path discovery model

使用准确率（Accuracy）作为模型的评价指标，对模型预测算法组件之间是否存在路径关系的性能进行评估。采用模型第2 层全连接层的输出并使用sigmoid 函数进行归一化，作为路径存在的概率，并划定阈值，作为依据概率判断路径是否存在的依据。实验中，存在路径的阈值定为0.85，不存在路径的阈值定位0.15。最终，在训练至第300 次时，模型准确率达到最高为0.95，训练集损失值最低为3.98，在测试集上的最高准确率达到0.72。

由结果可知，模型可以较好地拟合根据先验路径关系构建的训练数据，并在测试集上具有较好的泛化能力，说明模型可以较好地建立从源代码中的路径关系到算法代码结构与语义信息的联系。进一步选取聚类所得到的6 类算法步骤，从中进行算法路径挖掘，步骤如下。

1）从聚类得到的第一个类簇#0 出发，遍历其余所有聚类得到的功能集合。

2）遍历类簇#0 中的算法组件。

3）对于其中的每个组件，计算和后一个类簇中的所有组件形成路径的概率。

4）选取概率最高的组件对，将当前的算法组件添加到路径，并从组件对中属于下一个类簇的组件开始，计算和后一个类簇中的所有组件形成路径的概率。

5）如果当前组件和下一类簇的所有组件都无法形成路径，则跳过下一类簇。

6）重复步骤3）～4），直到对聚类得到的所有类簇遍历完成。

基于以上步骤，能挖掘出所有的功能集合中可组成算法路径的概率最大的算法组件集。在挖掘完成后，还可以通过从聚类类簇中去掉已经挖掘出的算法步骤，重复执行算法，挖掘出所有可能的算法路径。

从表3 中聚类得到的算法功能类别数据，进行算法路径的构建。选取所构建出概率最大的路径，如表5 所示。

表5 算法组件间的路径发现结果Tab.5 Results of path discovery among algorithm components

根据路径概率，可计算该条算法路径形成的置信度为0.904，为聚类数据中置信度最高的路径。分析所构建的路径，发现模型能够利用训练数据中算法组件结构与序列信息之间的先验数据，将结构与语义最为匹配的算法组件挖掘出来，构成算法流程。

基于路径发现模型，可以有效构建出算法流程中所需要的所有算法组件，形成算法步骤。然而，这些算法步骤之间并没有顺序关系，因此，进一步构建路径自组织模型，基于所发现的所有算法步骤，对其中的算法组件进行排序，从而最终实现算法的自组配。

3.3 基于排序的算法路径自组织

训练数据来源于拆分后的算法组件及其源代码，以源代码中算法组件的调用顺序作为算法路径构建中算法组件顺序的先验知识来源，统计数据如图6 所示。

图6 排序数据集的统计Fig.6 Statistics of ranking datasets

对于同一个流程中不同的算法组件，本文对组件进行遍历构建组件三元组，三元组包括算法流程中的两个算法组件，以及源代码的所有组件。将三元组中，组件1 排序靠前的作为正例，组件2 排序靠前的作为负例；在三元组的基础上，进一步根据组件在算法流程中的顺序，获得其中组件1与组件2 的排序得分。排序分数的范围来源于排序数据集中包含最多算法组件的算法流程中算法组件数。根据所统计的排序数据集，制定排序分数范围为Score=range(0，25)。对于算法流程中的算法组件di，如果它在算法流程中的排序为i，其排序得分Si=max(Score) -i。在三元组的基础上，加入组件1 与组件2 的排序得分，形成包括组件1、组件2、源代码组件集合和组件得分这4 个元素的数据，作为数据集中每条数据的字段。最终构建的路径自组织数据集共包含正负例各2 316 条数据。研究采用4∶1 的比例划分训练集与验证集，在模型上进行训练并验证模型对算法对排序的性能。

本文采用表6 所示参数初始化路径自组织模型。

表6 路径自组织模型的初始化参数Tab.6 Initialization parameters for path self-assembling model

使用准确率作为对模型预测组件对排序的评价指标，对模型预测某一算法路径中算法步骤顺序的性能进行评价。其中，针对模型输出的对算法组件对的排序，采用模型输出二元排序分数的全连接层的输出，并划分阈值，作为排序打分。其中，组件1 排序高于组件2 排序的阈值设置为0.85，组件1 排序低于组件2 排序的阈值设置为0.15。在模型训练过程中，采用早停策略，在第40 个epoch 时，模型在测试集上的准确率达到0.92，在训练集上的准确率达到0.98。模型训练过程中的损失值最低为0.17。

依据本节所构建的自组织模型，进一步使用3.2 节中的算法组件集构成的路径，依据算法组件间的排序分值对其进行自组织，最终构建出自组配的算法路径，以验证算法路径自组织模型的有效性。基于表5 中的路径步骤数据，路径自组织模型给出其中算法组件对的排序概率分值，如表7所示。

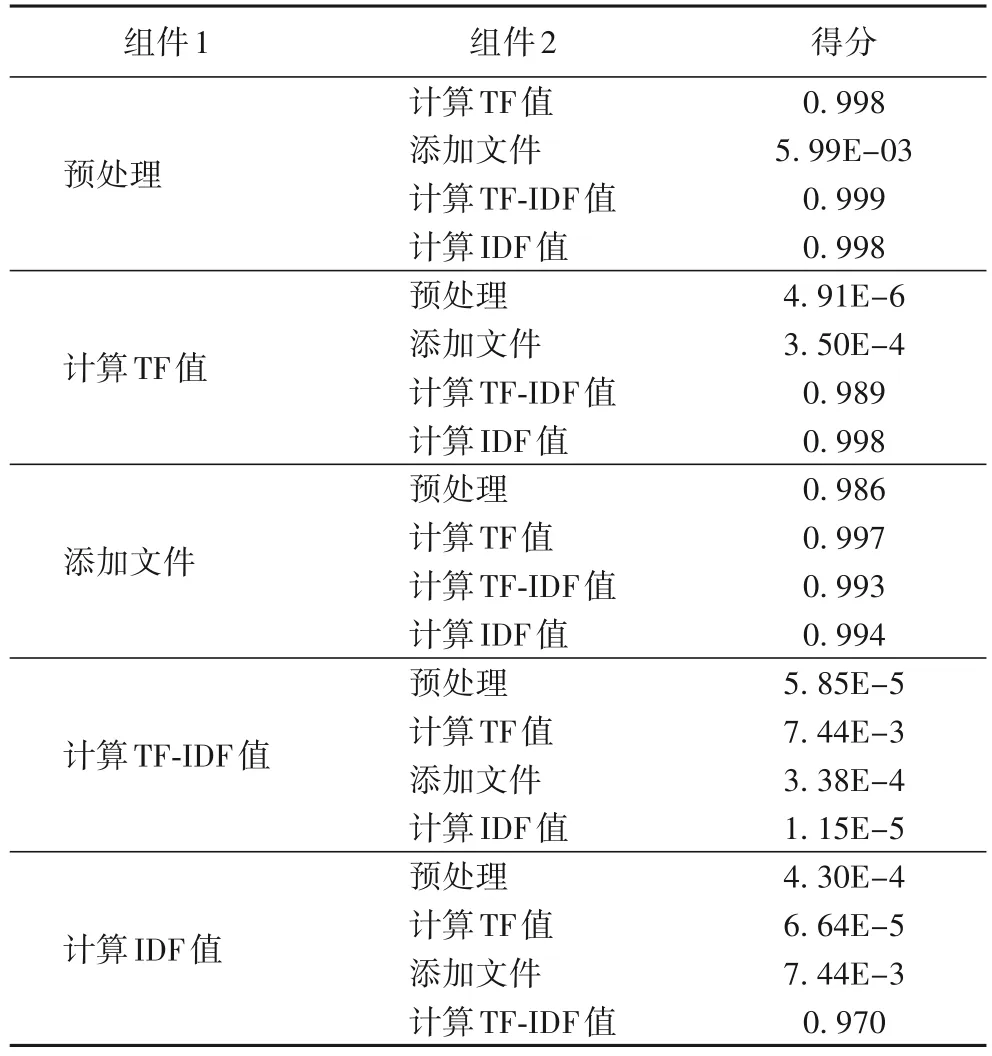
表7 算法组件对间的排序分值Tab.7 Ranking scores among pairs of algorithm components

根据排序算法，输出最终的算法路径，如表8 所示。根据模型输出的分值数据，可以看到，模型能够很好地利用从算法源代码中所学到的先验路径排序知识，对形成算法路径的组件输出正确的排序，从而实现算法路径中不同算法步骤的自组织，最终实现算法自组配，生成正确的算法流程路径。为了进一步验证所提出的算法自组配流程的有效性，选取更为复杂的决策树算法，对其拆分后的代码组件进行组配。拆分得到的决策树算法组件统计如表9 所示。

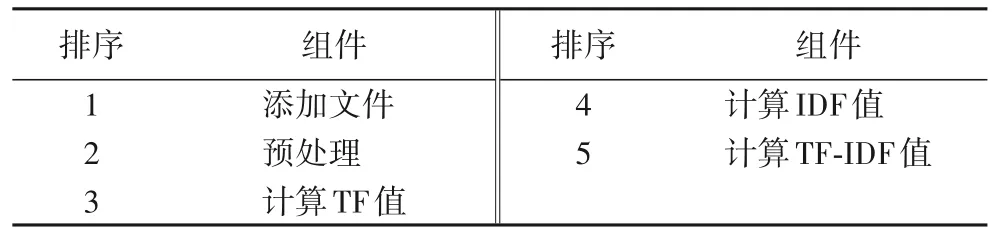
表8 TF-IDF算法组件自组配结果Tab.8 Component self-assembling results of TF-IDF algorithm

表9 决策树算法组件统计Tab.9 Component statistics of decision tree algorithm

对决策树组件进行组配，输出的算法路径功能步骤组配结果为：1）读取txt；2）划分数据；3）计算信息熵；4）计算信息增益；5）ID3 选择特征；6）多数决定叶子节点分类；7）生成树。

分析组配得到的结果可以看到，更为复杂的决策树算法上，从拆分得到的组件集合中，模型都能够很好地挖掘功能不同的组件子集，并通过路径发现与排序模型对算法组件进行自组织，最终生成顺序正确的算法流程，验证了本文所构建的算法自组配方法的有效性。

3.4 面向业务需求的算法路径自组配

本文评估基于单个业务需求，对于面向业务流程的自组配评估，仅需对流程上的各个步骤的评估指标进行平均即可得到业务流程的评估结果，因此采用的评估方式基于单个业务需求。

对于业务需求q最终组配得到的算法代码，评价指标由代码自组配系统的召回率Rec（Recall）与平均精确度AP（Average Precision）联合给出：

其中：GroundTruth为人工标注的所有相关的算法数；p@k为第k个样本时的精确度；rel@k用来评估第k个样本是否与检索相关，如果相关则为1；Rh表示召回的所有算法组件；Rt表示召回的组件中正确的组件数。

在实际实验中发现，对于特定业务需求，算法代码自组配系统首先根据算法代码的向量表示检索相关的算法组件，并进行自动组配。然而，算法组件组配的路径并不唯一，即对于同一需求，可能存在多条合理的算法组配路径实现这一需求，而自组配系统基于算法代码表示，给出其中的一条路径，因此使用人工制定的标准进行评估，难以对每个需求都制定一个标准代码检索结果与组配路径，导致使用上述评估指标时，自动算法组配的指标计算值过低。

因此，对上述评分公式进行改进。改进后的评分公式不进行精确匹配，而对功能相似度进行匹配。对于排序@k（@表示top）上的代码组件，如k1为人工选取的代码组件，k2为自动组配系统选取的代码组件，其相似度sim(k1，k2)为：

其中：代码组件的向量由网络表示模型给出，vec（）表示向量，如vec(k1)就是指代码组件k1的向量。基于上述相似度计算公式，改进后的代码评分准则中召回率、精确度的计算基于相似度阈值而非精确匹配，其中，判断自动组配系统给出的候选代码组件与人工给出的候选代码组件是否一致的标准由rel@k给出，即：

其中threshold为人工设定的相似度阈值。

本文在所有算法组件数据集的基础上共构建了3 个自然语言描述的业务需求作为检索条件，并基于业务需求，人工选取排名靠前的20 个算法组件，作为最优检索排序，并分别使用基线模型与本文提出的检索模型分别面向所构建的业务需求进行检索。其中，研究所构建的业务需求分别为：

query1：“给定多篇txt 格式的文本，读取文本，并使用BM25 对读取后的文档进行排序”。

query2：“基于一篇或多篇txt 格式的文本，使用textrank算法，从文本中包含的内容中提取关键词”。

query3：“给定语料库，其中包含多篇文本，每篇文本有多行文字，每行文字代表一句话，其中词由空格隔开，使用word2vec 算法获取其中的词向量”。

在此基础上，选取信息检索领域常用的检索模型作为基线模型，与本文方法进行对比。本文所采用的基线模型为基于关键词的BM25（Okapi BM25）排序算法，定义如式（20）所示：

其中：k、b为可调节的参数，|D|为检索的文档的长度，即为算法组件的词袋表示的长度，avgdl为文档的平均长度。在基于BM25 的方法中，仅对业务需求的自然语言描述进行分词，将分词后获得的词作为语素，从算法代码的词袋表示中，使用字符串匹配的方式进行检索并计算BM25 分值，作为基线模型。

在实际检索时，由于本文所构建的算法代码库大多基于英文，因此首先将所制定的query 转为英文，采用检索得到的算法组件，并依据相关性筛选出相关性过低的组件，将算法组件输入本文所构建的路径发现与自组配模型中，得到自组配的算法流程。基于上述评价指标，分别使用不同的算法组件表示方法进行实验，并分析最终构建出的路径的结果。基于路径发现与自组配模型，本文构建了3 种不同的表示模型进行实验：基于BM25 检索与词袋表示的模型；基于语义扩充检索与词袋表示的模型；基于语义扩充检索与融合结构、序列表示的模型。基于上述评价指标，实验结果如表10所示。

表10 基于不同表示方法的检索对比实验结果Tab.10 Comparative experiment results on retrieval based on different representation methods

分析结果可见，本文所采用的模型与传统的排序算法相比有较大的提升。在基本结构相似的情况下（对向量的表示均采用skip-gram/cbow 结构），本文所构建的检索方法能够较大地提升检索结果中相关算法组件的数量，从而显著提高算法组配的结果，而传统排序算法仅仅基于分词后的词相关度进行排序，因此无法针对算法的语义与结构进行检索。仅使用词袋方法进行语义表示的代码表示方法，无法有效利用算法的结构信息，因此无法形成有逻辑的组配路径，而本文排序模型来源于源代码的先验知识，与使用传统的表示方法相比，有较大的提升，说明算法代码组件及其资源的结构与语义知识对于算法的自组配有较大的作用。

4 结语

本文构建了算法路径自组配模型，为实现算法结构化管理提供依据。首先，基于情报工程算法平台，对代码以最小可复用单元进行拆分，使它与业务步骤相对应，为算法组配的实现奠定基础；接着，结合AST 和CFG 等对算法代码进行结构提取，并使用GCN 和word2vec 对算法组件进行图向量表示；然后，在此基础上使用聚类模型进行步骤挖掘，通过组件对融合向量计算进行组件间路径发现；最后，使用排序算法实现算法路径自组配。

基于本文提出的自组配算法得到算法组件的自组织路径后，仍有部分算法组件间的输入输出无法完全使用自动化的方式进行数据流的传输，需要人工介入对数据类型的调整来进行算法管道构建。在未来的工作中，将进一步对算法组件间数据的规范化进行研究，并结合现有自动机器学习技术，如超参数搜索等，进一步构建效率更高的算法自组配系统。