基于MDP-ADMM的数据中心储能系统优化运行方法

陈绪昌，王育飞，薛 花

（上海电力大学电气工程学院，上海 200090）

随着移动互联网、云计算和人工智能等先进信息技术的快速发展，作为支撑信息技术的核心基础设施，数据中心的规模也在不断扩大[1]。中国数据中心机架总规模在2016—2021 年间保持快速增长，年均增速已超过30%。截至2021 年底，中国数据中心机架总规模已突破500 万架[2]。数据中心作为电力系统中一类高能耗工业用户，其购电成本是制约数据中心经济运行的关键因素[3]。同时数据中心过高的负荷峰谷差还会给配电网运行调度增加难度，影响配电网的高效运行[4]。

为了保障数据中心供电可靠性，可以配置储能系统用作市电供电故障情况下的紧急备用电源。在保证数据中心充足的紧急备用容量基础上，可以通过冗余配置储能系统容量使其参与数据中心日常运行[5]。储能系统可通过“低储高放”策略，即在电力负荷电价较低时段充电，在电力负荷电价较高时段放电[6]，有效缓解数据中心购电成本高和负荷峰谷差大的问题。因此，研究数据中心储能系统的优化运行方法，对提升数据中心的运行效率具有重要意义。

目前，国内外学者已经对数据中心储能系统优化运行方法开展了大量研究。文献[7]基于李亚普诺夫优化算法，设计了一种数据中心储能系统在线优化控制方法，在降低数据中心购电成本的同时也提升了可再生能源的利用率。文献[8]设计了一个利用储能系统降低数据中心峰值负荷的优化框架，并基于模型预测控制对储能系统的充放电功率进行实时调整。文献[9]建立了一种考虑储能系统与数据中心在微电网中协调运行的优化模型，并采用混合整数线性规划对其求解，以降低数据中心运行成本。文献[10]以数据中心的购电成本最小为目标，建立了数据中心的能量管理策略框架，根据电力市场电价的实时变化，对储能系统的充放电策略进行优化。上述研究在优化数据中心储能系统运行策略时，将数据中心电力负荷视为不可调节负荷。然而，数据中心电力负荷具备在时间上灵活调节的潜力，数据中心通过将数据处理任务在时间上转移可以实现电力负荷的灵活转移[11]。利用该负荷转移特性，数据中心可以对自身的电力负荷进行动态调节，从而可以协同储能系统对数据中心购电成本进行削减以及降低负荷峰谷差，而目前却很少有研究利用该特性对数据中心储能系统的运行策略进行优化。

数据中心储能系统优化运行模型具有高维非线性的特点，并且模型中存在大量多时段耦合约束，采用传统智能算法对其进行求解会出现收敛速度慢以及陷入局部最优的问题[12]。马尔可夫决策过程(Markov decision process，MDP)可以利用相邻时段的状态转移关系，实现多时段耦合问题的解耦[13]。交替方向乘子法(alternating direction multiplier method，ADMM)可以将一个问题拆解成若干个子问题进行求解，降低问题求解的复杂度，加快收敛速度[14]。文献[15]构建了基于MDP的机电设备动态可靠性评价模型，通过观测到的设备运行信息，对机电设备可靠性状态进行评估。文献[16]提出了基于MDP的电动汽车充电站能量管理策略，有效降低充电站日运行成本，同时也满足了电动汽车用户的充电需求。文献[17-18]建立了基于ADMM的配电网分布式鲁棒优化调度模型，在有效应对分布式电源出力不确定的同时，也提升了配电网调度的经济性。MDP 和ADMM 在上述机电设备可靠性评估、电动汽车有序充电、配电网优化调度等领域得到了广泛应用。然而，目前很少有MDP和ADMM在储能系统优化运行方面的研究。

考虑到数据中心电力负荷能够在时间维度上灵活转移的特性，以综合运行成本最小和削峰填谷效果最佳为目标，建立数据中心储能系统优化运行模型，设计一种MDP 和ADMM 相结合的算法对上述优化运行模型进行求解。在MATLAB中进行仿真分析，验证所提优化运行方法的有效性与合理性。

1 数据中心基本结构与负荷转移特性分析

1.1 数据中心基本结构

数据中心可看作一个集大数据运算和存储为一体的高性能计算机的集中地，能够为互联网用户提供数据处理和存储服务[19]。数据中心的基本结构如图1所示，主要由服务器设备、通信存储设备、制冷设备、储能系统、公共电网以及相关的控制和调度系统等部分组成。

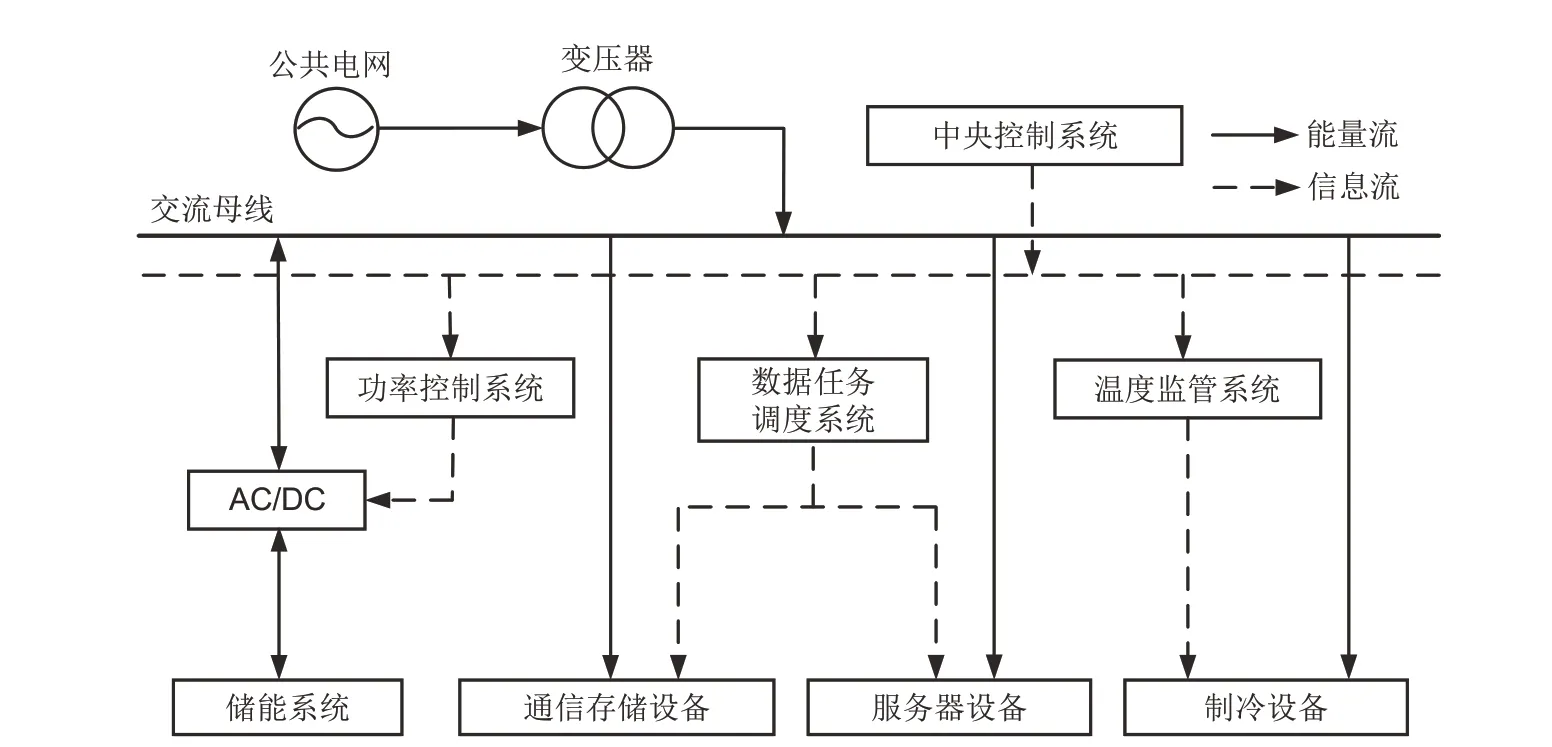
图1 数据中心基本结构Fig.1 Basic structure of data center

数据中心通信存储设备负责接收和存储互联网用户发送的各类数据处理任务。服务器设备则需对用户的数据处理任务进行处理，其在处理数据处理任务时会消耗大量的电能。同时，由于服务器设备工作时会产生大量的热量，因此需通过制冷设备对数据中心机房的温度进行调节以维持服务器设备运行在适宜温度范围内。而公共电网和储能系统作为数据中心供电电源，在常规运行模式下，公共电网和储能系统同时向数据中心的负载供电，储能系统根据数据中心功率需求情况以及分时电价信息进行充放电操作。而当数据中心市电出现故障时，此时储能系统将作为后备电源向数据中心的负载供电。

1.2 数据中心负荷转移特性分析

数据中心总功耗主要由服务器设备功耗、制冷设备功耗和通信存储设备功耗三个部分构成[20]。因此，数据中心的总功耗可通过式(1)计算：

式中，PIDC,t为t时刻数据中心的总功耗；PIT,t为服务器设备功耗；PCO,t为制冷设备功耗；PNW,t为通信存储设备功耗。

服务器设备功耗与其利用率正相关，t时刻数据中心服务器设备功耗可通过式(2)计算[21]：

式中，Pidle和Ppeak分别表示单组服务器空载和满载功耗；Dt为t时刻服务器设备所处理的数据处理任务量；-ψt表示服务器设备在t时刻的利用率；N为数据中心服务器组的数量；μ为单组服务器每小时处理的数据处理任务量，即处理速率。

制冷设备通过对数据中心机房温度进行调节，从而使服务器设备运行在要求温度范围内。数据中心制冷设备功耗可通过式(3)计算：

目前在数据中心机房的温度热力学仿真中常采用等效热参数模型[22]，即数据中心机房的室温变化特性可通过式(4)描述：

通信存储设备功耗与数据中心服务器数量正相关，而处理数据处理任务量的变化对其影响可以忽略[23]，因此数据中心通信存储设备功耗可通过式(5)计算：

式中，ω为通信存储设备的能耗系数。

基于对数据中心主要设备的功耗分析，服务器设备的功耗与其处理的数据处理任务量正相关，通过改变数据处理任务处理量可以直接对服务器设备功耗进行调节。制冷设备功耗与服务器设备的功耗在时间上是相互耦合的，通过改变数据处理任务处理量可以间接调节制冷设备功耗。因此，数据中心的总功耗可以抽象为关于数据处理任务处理量的函数PIDC,t=f(Dt)，对数据中心功耗的调节，本质上是对处理的数据处理任务量进行动态调整。

根据用户对服务质量要求存在的差异性，可以将用户发送的数据处理任务划分为延迟敏感型数据处理任务和延迟容忍型数据处理任务两类。延迟敏感型数据处理任务(如网络搜索、即时通信等)对响应的实时性要求较高，此类数据要求数据中心无延时地响应计算并进行处理，因此不允许在时间上进行转移；而延迟容忍型数据处理任务(如大规模数据分析、数字图像处理等)对实时性要求不高，此类数据处理任务只需在规定时间之前处理完成即可，故可在允许的时间限度内进行转移。

对于在t时段数据中心接收到的延迟容忍型数据处理任务，假设其最大允许转移时间尺度为Tmax，则可在t～(t+Tmax)时段内对其迁移而不影响用户的满意度。因此在满足用户满意度的前提下，通过对延迟容忍型数据处理任务在时间上进行转移，可实现数据中心电力负荷的转移。利用该负荷转移特性，数据中心可以将峰电价时段的电力负荷转移至谷电价时段从而降低数据中心的购电成本，或者将高峰时段的电力负荷转移至低谷时段从而起到削峰填谷的效果。

2 考虑负荷转移特性的数据中心储能系统优化运行模型

为了提升数据中心运行的经济性和可靠性，基于数据中心负荷转移特性分析，以数据中心综合运行成本最小和削峰填谷效果最佳为目标，建立考虑负荷转移特性的数据中心储能系统优化运行模型。

2.1 目标函数

第一个优化目标为数据中心在运行周期内的综合运行成本最小，包括数据中心的购电成本和储能系统损耗成本，目标函数如式(6)所示：

式中，Cele为运行周期内数据中心的购电成本；Closs为储能系统的损耗成本；κt为t时刻的电价；T= 24 h，表示运行周期；Δt= 0.5 h，表示优化步长；Pg,t为数据中心t时刻在电网侧的净负荷；EBESS和PBESS分别为储能系统的额定容量和额定功率；cs和cp分别为储能系统单位容量和单位功率投资成本；Eloss,t为t时段储能系统充放电容量损耗；Nd为储能系统在放电深度为d时的循环寿命。

其中，储能系统的循环寿命Nd与其放电深度d之间的关系可以用幂函数表示[24]，如式(7)所示：

数据中心在t时刻在电网侧的净负荷Pg,t可通过式(8)计算：

式中，Pcha/dis,t为储能系统在t时刻的充放电功率，Pcha/dis,t≥0 表示储能系统充电，Pcha/dis,t< 0 表示储能系统放电；ηcha和ηdis分别为储能系统充电效率和放电效率。

第二个优化目标为数据中心削峰填谷的效果最佳，用电网侧净负荷方差来表征削峰填谷效果，目标函数如式(9)所示：

式中，Pav为数据中心在整个运行周期内净负荷功率平均值。

2.2 约束条件

数据中心在t时段接收的延迟容忍型数据处理任务量与转移至后续时段延迟容忍型数据处理任务量总和相等，即需满足式(10)约束：

式中，λt为t时段数据中心接收的延迟容忍型数据处理任务量；at,j表示数据中心在t时段向j时段转移的延迟容忍型数据处理任务量。

由于服务器设备计算能力有限，须保证数据中心实际处理的数据处理任务总量不能超过服务器设备计算容量限制，即服务器的平均负载率须满足式(11)约束：

式中，-ψmax为服务器设备的最大负载率。

对于未能及时处理的数据处理任务，需存储在通信存储设备中等待后续时段处理。为了避免通信存储设备存储的数据处理任务量超出容量上限，其存储的数据处理任务量需满足式(12)约束[25]：

式中，Qt为t时段存储的数据处理任务量；Qmax为通信存储设备的存储容量上限；ζt为t时段数据中心接收的延迟敏感型数据处理任务量。

数据中心在运行过程中，为了保证服务器设备的工作性能，数据中心机房温度必须限制在一定范围内，即数据中心机房温度需要满足式(13)约束：

式中，θmax为数据中心机房运行温度上限。

储能系统的充放电功率不能超过其额定充放电功率，同时为了保证数据中心供电可靠性，储能系统的剩余电量需保证数据中心市电故障时为其持续供电一段时间，即储能系统运行时需满足式(14)约束：

式中，Et为t时段储能系统剩余电量；ΔTsus为供电系统失电时，储能系统需保证数据中心正常运行最低时长要求。

3 基于MDP-ADMM 算法的储能系统运行策略优化

所建立的储能系统优化运行模型具有多时段耦合的特性，在求解过程中将引入大量时段耦合约束。同时，引入的多时段耦合约束，如服务器设备的负载率约束、通信存储设备的存储容量约束等均为非线性约束条件，因此所建立的储能系统优化运行模型本质上是非线性规划模型。在对该模型进行求解时，需确定运行周期内每个时段储能系统充放电功率、处理的两类数据处理任务量、转移至后续各时段的数据处理任务量等，因此该模型的解空间为一个高维向量空间。直接求解该模型计算规模大、求解效率低。因此，在求解该模型前，需要先将模型中的时间段耦合约束进行解耦，将多时段优化问题转换成单时段优化问题进行迭代求解，从而对储能系统运行策略进行优化。

3.1 基于MDP的多时段解耦方法

本工作考虑将原问题建模为马尔可夫决策过程，从而将多时段优化问题转换为一系列单时段优化问题，然后利用相邻时段之间的耦合及约束关系对单时段优化问题逐时刻求解。马尔可夫决策过程建模主要包括状态空间(S)、动作集合(M)、状态转移函数(T)和回报函数(R)四个部分。

状态空间(S)表征当前时段各设备的状态信息，在优化当前时段运行策略时，各设备的状态信息也会随之发生改变。为了避免设备状态超出约束范围，需对通信存储设备所存储的数据处理任务量、服务器设备负载率和储能系统剩余电量予以考虑，即t时刻状态空间St的定义如式(15)所示：

动作集合(M)由一系列决策变量(X)进行表征，表示在状态St下所制定的运行决策，即为t时段处理的数据处理任务量以及储能系统的充放电功率。因此，t时段动作集合所映射的决策变量可通过式(16)表示：

状态转移函数(T)用以表征相邻两个时段各设备状态的变化关系。利用相邻段的耦合关系以及当前时段所给定的动作，从而可对下一时段数据中心各设备的状态空间St+1进行求解，如式(17)所示：

式中,St(m)表示状态空间St中的第m个元素；Xt(n)表示决策变量Xt中第n个元素。

考虑到数据中心接收到的数据处理任务量不确定因素影响，两类数据处理任务量的不确定性可以通过式(18)表示：

式中，λ̂t+1和ζ̂t+1分别表示延迟容忍型和延迟敏感型数据处理任务量的预测值；Δλt+1和Δζt+1分别表示延迟容忍型和延迟敏感型数据处理任务量的预测误差。

回报函数(R)表征在状态空间St下执行动作Mt时所能立即产生的回馈值，其直接影响当前时刻最优策略的选取。本工作所建立的回报函数将两个目标函数单时段取值分别进行归一化后，再进行线性加权来表示。

归一化处理方式如式(19)所示：

式中，Ft为目标函数在t时段的单时段值；Fmint和Fmaxt分别为运行周期内目标函数的最小和最大单时段值。

对归一化后的目标函数进行加权，得到的回报函数如式(20)所示：

式中，Rt表示在t时刻由状态St在运行决策Xt下转移至状态St+1时的回报值；α和β为权重系数。

3.2 基于ADMM的运行策略优化

通过MDP 将原问题进行多时段解耦重构后，采用ADMM 对重构后的优化问题进行求解。ADMM是近年来兴起的一种分散优化算法，具有收敛性好、收敛速度快等优点。ADMM融合对偶上升法的可分解性以及乘子法较好的收敛性，其核心是将一个大的问题分解成若干个小问题，交替迭代进行求解，从而极大降低问题求解的复杂度。

在将重构后的问题进行分解前，需定义一个耦合变量Yt对回报函数的其中一个决策变量Xt进行替代，从而构造出关于回报函数的增广拉格朗日函数，如式(21)所示：

式中，ρ为拉格朗日乘子；δ为惩罚因子，其取值为大于0的常数。

其中，式(11)～(13)为非线性约束条件，本工作采用逐次线性化方法对非线性约束条件进行线性化，即在每一次迭代过程中，对非线性约束条件在决策变量迭代值处进行泰勒展开，保留一次线性项[26]。

根据ADMM 求解流程，可将增广拉格朗日函数分解成两个交替迭代求解部分，如式(22)和式(23)所示：

式中，X(k+1)和Y(k+1)分别为决策变量和耦合变量在第k+1 次迭代后的值；ρ(k)为拉格朗日乘子在第k次迭代后的值。

拉格朗日乘子的迭代值可通过式(24)计算：

若残差满足迭代收敛判据则停止迭代，迭代收敛判据 式(25)所示：

式中，r(k+1)为第k+1 次迭代后的残差；ε为收敛精度。

ADMM算法的求解流程如图2所示，具体求解步骤如下。

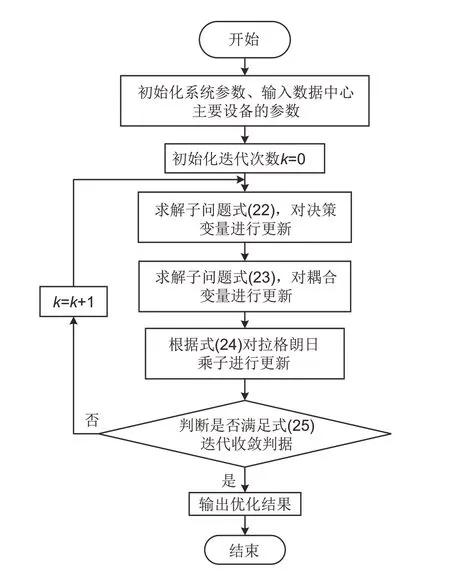
图2 ADMM算法求解流程图Fig.2 Flow chart of ADMM algorithm solving process

步骤1：初始化系统参数。输入数据中心主要设备参数，包括储能系统参数、服务器设备参数和制冷设备参数等。初始化决策变量X(k)、耦合变量Y(k)和拉格朗日乘子ρ(k)，迭代次数k=0。

步骤2：令耦合变量Y=Y(k)，将其代入子问题式(22)求得决策变量第k+1次迭代后的结果X(k+1)。

步骤3：令决策变量X=X(k+1)，将其代入子问题式(23)求得耦合变量第k+1次迭代后的结果Y(k+1)。

步骤4：将步骤2 和步骤3 求解的结果代入式(24)，从而对拉格朗日乘子ρ(k+1)进行迭代更新。

步骤5：通过式(25)计算第k+1 次迭代后的残差，验证残差是否满足迭代收敛判据。若满足收敛判据，则结束迭代，否则更新迭代次数k并返回到步骤2进行下一次迭代计算。

4 算例分析

4.1 基础参数设置

选取某大型数据中心作为研究对象进行仿真分析，相关仿真参数设置如下：数据中心配置40 组同构的服务器组，单组服务器的空载功耗Pidle和满载功耗Ppeak分别为10 kW和40 kW，服务器设备的最大负载率-ψmax为0.9，数据中心机房运行温度上限θmax为23 ℃。储能系统的额定功率为3000 kW，额定容量为3000 kWh。储能系统的单位容量和单位功率投资成本分别为1500 元/kWh 和1100 元/kW。储能系统的充电效率ηcha和放电效率ηdis均设置为0.9。延迟敏感型数据处理任务不可进行转移，延迟容忍型数据处理任务最大允许转移时间尺度为3 h，数据中心处理不同类型数据处理任务的原始功率需求情况如图3 所示，电网购电电价采用江苏省2022年7月分时电价[27]。

图3 数据中心功率需求Fig.3 Power demand of data center

4.2 仿真结果分析

分别采用PSO 算法、ADMM 算法和所提的MDP-ADMM算法进行20次独立的运算。其中，适应度函数即为论文所构造的回报函数，设置权重系数α= 0.5 和β= 0.5。3 种算法的迭代曲线和性能比较分别如图4和表1所示。

表1 3种算法性能对比Table 1 Comparison of performance of three algorithms

图4 3种算法的迭代曲线Fig.4 Iteration curves of three algorithms

从图4 中可以看出，MDP-ADMM 算法仅经过13 次迭代即收敛于全局最优解，而传统的ADMM算法和PSO分别经过33次和58次迭代才收敛于全局最优解，MDP-ADMM 的收敛速度显著快于其他两种算法，这是由于所提算法通过对多时段耦合约束进行解耦以及对问题进行分解，极大地降低了模型求解的复杂度。在PSO算法的迭代收敛曲线中，算法两次收敛于局部最优解，而MDP-ADMM则直接收敛于全局最优解，这是因为该算法通过决策变量和耦合变量之间的交替迭代，使其搜索半径扩大为两者之间的欧式距离，相比于PSO 算法，具有更大的寻优范围，避免问题陷入局部最优。

从表1中适应度值标准差和达到最优解次数占比可以看出，MDP-ADMM 每次求解的适应度值波动最小，并且收敛于最优解的概率最大，这表明了所提算法在求解稳定性方面优于其他2种算法。

MDP-ADMM 算法的收敛性取决于迭代过程中残差值的变化，图5 为MDP-ADMM 算法的残差收敛曲线，收敛精度ε设置为0.05。从图5 中可以看出，在第13次迭代时，MDP-ADMM算法的残差值降至0.048，满足式(25)的迭代收敛判据，证明所提算法经历13次迭代即可收敛。

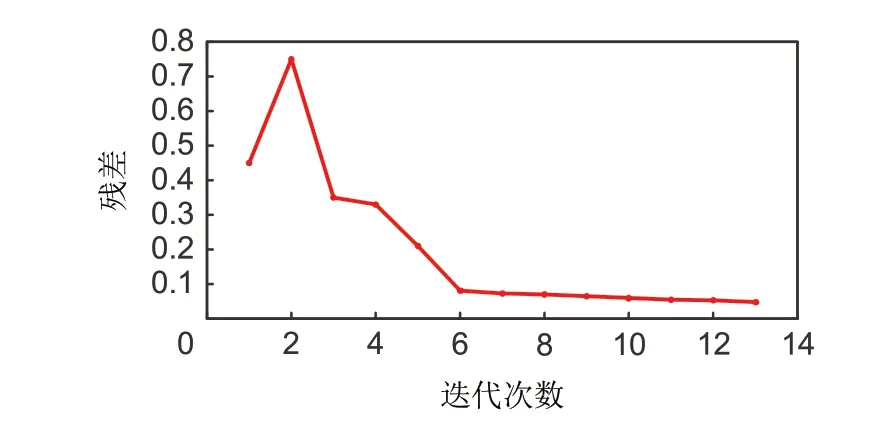
图5 MDP-ADMM算法的残差收敛曲线Fig.5 Converge curve of residual error of MDPADMM algorithm

基于以上3种算法求解得到的总体优化结果如表2 所示，3 种算法求解的净负荷功率曲线如图6所示。从表2 可以看出，相比PSO 算法和ADMM算法，通过MDP-ADMM算法对优化运行模型进行求解，综合运行成本分别降低了15.6%和10.2%，进一步提升了数据中心运行的经济性。同时结合图6 所示3 种优化算法下数据中心电网侧净负荷曲线可以看出，MDP-ADMM 算法较大程度降低了电网侧净负荷峰谷差，减小了对电网运行的冲击。

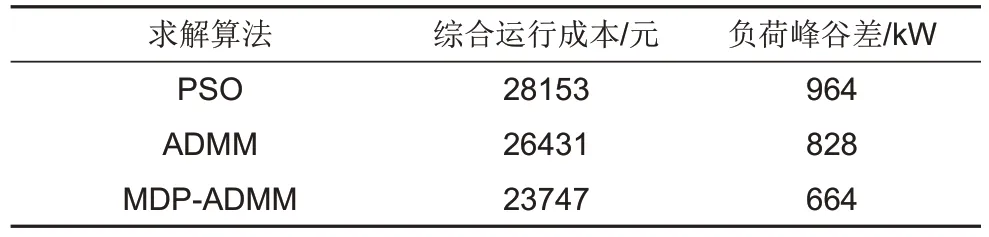
表2 3种算法的优化结果对比Table 2 Optimal results comparison of three algorithms

图6 3种算法求解的净负荷功率曲线Fig.6 Power curve of grid optimized by three algorithm

为了验证所提优化运行方法的有效性，对利用MDP-ADMM 算法求解出的优化结果进行具体分析。图7为数据中心处理不同类型数据处理任务的用电功率需求情况，从图7中可以看出，在0∶00～7∶00 时，电价为谷时电价，数据中心的电力负荷处于谷时段。此时，数据中心对该时段接收到的延迟容忍型数据处理任务及时进行处理而基本不发生转移，这一方面可以以最小的购电成本完成对延迟容忍型数据处理任务的处理，另一方面可以最大程度满足用户的服务质量要求。在8:00—12∶00 时，电价为峰时电价，数据中心将此区间延迟容忍型数据处理任务转移至12∶00—16∶00 时段处理，以降低数据中心购电成本。在18∶00—22∶00 时，数据中心电力负荷处于峰时段，此时电价为峰时电价，为了起到削峰效果，该时段的延迟容忍型数据处理任务会转移至电力负荷较轻的22∶00—24∶00 时段进行处理。同时，由于分时电价差异，通过将峰时段的数据处理任务转移到低电价时段进行处理，可以较大程度降低数据中心的购电成本。

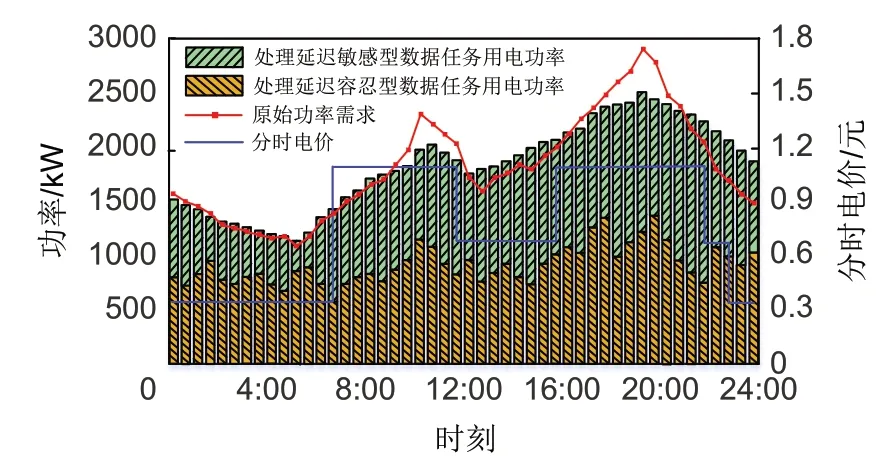
图7 数据中心功率需求Fig.7 Power demand of data center

图8 为储能系统在运行周期内的充放电功率，从图8中可以看到，储能系统整体上在电价较低时段进行充电，在电价较高时段进行放电。在充电时段中，0∶00—7∶00时段的电价为谷时电价，储能系统以较低的充电费用进行充电，这一方面起到了电力负荷填谷的效果，另一方面也为后续时段的放电提供了充足的电量。而在11∶00—12∶00和17∶00—21∶00时段，电价为峰时电价，在这期间储能系统通过放电实现购电成本削减。但是由于数据中心对供电可靠性的要求，储能系统必须保留充足的电量以保证市电故障时对数据中心的电能供应。而在这期间，数据中心利用负荷转移特性实现用电功率的削减，从而降低了数据中心对储能系统备用电量的需求，使储能系统有更充足的电量投入数据中心的经济运行。

图8 储能系统充放电功率Fig.8 Charging and discharging power of energy storage system

为进一步分析负荷转移特型对储能系统运行策略的影响，对比分析延迟容忍型数据处理任务不同转移时间尺度下储能系统的运行策略。从图9中可以看出，在两种不同的转移时间尺度下，储能系统整体上在电价较低时段进行充电，在电价较高时段进行放电。随着转移时间尺度增大，数据中心综合运行成本由22817元降至21541元，净负荷峰谷差由573 kW降至505 kW。这是由于随着可转移时间尺度的增大，延迟容忍型数据处理任务可以被转移至后续更多时段进行处理，从而提高了数据中心电力负荷在时间上的调节潜力，这也使储能系统充放电更加灵活。因此，在优化数据中心储能系统运行策略时，需充分考虑数据中心负荷转移特性，从而可以进一步提升数据中心运行的经济性和可靠性。

图9 不同转移时间尺度下储能系统充放电功率Fig.9 Charging and discharging power of energy storage system under different shifting time scales

为了验证所提优化运行方法的鲁棒性，分析延迟容忍型和延迟灵敏型数据处理任务量在不同预测误差场景下的优化结果。假设两类数据处理任务的预测误差满足同一正态分布N(0,σ2)，优化结果如表3所示。

表3 不同预测误差下的优化结果Table 3 Optimal results with different prediction errors

从表3可以看出，随着数据处理任务量不确定性的提高，数据中心运行的经济性和可靠性都出现了下降。但是在同一不确定水平下，本工作所提出的优化运行方法经济性和可靠性最优，说明所提的方法能更好地应对数据处理任务的不确定性，具有更好的鲁棒性。

5 结 论

针对数据中心综合运行成本高和电网侧负荷峰谷差大这一问题，本工作考虑数据中心负荷在时间维度上的转移特性，以综合运行成本最小和削峰填谷效果最佳为目标，建立数据中心储能系统优化运行模型，采用MDP 和ADMM 相结合的算法对所提优化运行模型进行求解，经仿真验证，得出如下结论。

（1）利用数据处理任务在时间上的转移特性，可以对数据中心主要设备的功耗进行调节，从而有效地提升数据中心的运行效率，为数据中心能耗管理及优化运行提供了一种新的思路。

（2）通过仿真验证了所提优化运行方法兼顾了数据中心运行可靠性和经济性的结论，既能降低数据中心的负荷峰谷差，也显著地降低了数据中心的综合运行成本。

（3）对于所建立的多时段耦合的优化运行模型，采用MDP 与ADMM 相结合的优化算法进行求解，收敛速度、全局搜索能力以及求解稳定性均优于PSO 和传统ADMM，证明所提算法具有更好的求解效果。

本工作所提的优化运行方法是在确定环境下进行的，而实际中由于数据中心运行面临着多重不确定性，如接收数据处理任务量的不确定性等，在后续工作中可对这些不确定性因素予以考虑，对储能系统的运行策略进行实时优化。