基于组合预测的苏州市物流需求预测分析

吕婉琪，陆芬

摘  要：随着科技与国民经济的发展，物流早已作为人类生活的必需品贯穿于日常的各个层面。发展壮大物流业有利于提升国家经济运行效率，完善资源分配，推进企业的融资以及促进整个社会经济运行结构的调整。中国物流业发展迅速的背后是经济的支持，而产业结构的升级和经济的提质增效也离不开物流业的成长，经济发展与物流发展相辅相成。因此，为了更好地制定物流计划并推动经济发展，物流需求预测就显得十分重要。文章选取苏州市作为研究对象，通过运用苏州市的综合货运量与GDP等重要经济指标，分别在二次指数平滑法和回归分析预测法下进行综合货运量的预测，对比两种方法的相对误差，确定未来三年苏州市综合货运量的预测值，并对苏州市物流提出管理建议，以期为苏州市的经济发展提供借鉴。

关键词：物流需求预测；二次指数平滑法；回归分析预测法

中图分类号：F259.27    文献标志码：A

DOI：10.13714/j.cnki.1002-3100.2023.11.009

Abstract： With the development of science and technology and national economy， logistics has long been a necessity of human life throughout every level of daily life. The development and expansion of the logistics industry is conducive to enhancing the efficiency of national economic operation， improving resource allocation， promoting enterprise financing， and advancing the adjustment of the entire socio-economic operation structure. The rapid development of China logistics industry is supported by the economic， and the upgrading of industrial structure and the improvement of economic quality and efficiency can not be separated from the growth of the logistics industry. The development of economic and logistics complement each other. Therefore， in order to better formulate logistics plans and promote economic development， logistics demand forecasting is very important. Suzhou City is selected as the research object. By using the comprehensive freight volume， GDP and other important economic data of Suzhou， the comprehensive freight volume is predicted under the second exponential smoothing method and regression analysis prediction method. The relative errors of the two methods are compared to determine the predictive value of the comprehensive freight volume of Suzhou in the next three years， and the management suggestions for Suzhou logistics are put forward to provide reference for the economic development of Suzhou.

Key words： logistics demand forecast; second exponential smoothing method; regression analysis prediction method

0  引  言

隨着科技的进步和时代的更迭，物流业发展迅速。古有驿站传信，今有高科技自动机器人智能分拣快递，物流的技术可谓是日新月异。如今，为了促进销售、带动消费者的内需，商家经常举办促销活动。电商平台和快递行业的兴起，更是促进了消费者购买商品的热情。根据国家邮政局统计，2021年“双11”期间（11月1日至16日），邮政、中通等快递企业共揽收快递包裹68亿件，同比增长18.2%。“双11”当天，天猫总交易额为5 403亿元。由此可见，快递给人们生活带来的便利促进了物流行业的迅速发展，同时物流业的发展折射出了中国经济旺盛的内需、加速转型的步伐与广阔的发展潜力。

物流需求预测主要是为了引导和协调人们的物流管理活动，从而帮助人们采取适当的策略和手段来谋求最大的利益[1]。这意味着，精确的需求预测不仅可以促进物流信息系统和生产设施能力的计划和协调，还可以确定产品向配送中心、仓库或零售商进行分配的原则[2]。由于物流产业与经济不可分割的关系，因此对一个地区的物流需求进行分析与预测可以直观地看出该地区的经济发展情况：随着区域经济结构、资源配置、市场等多种经济因素的变化，区域的物流需求量、物流需求结构和物流需求层次也会发生相应的变化[3]。鉴于此，研究物流需求预测对于了解经济发展情况十分重要。

关于物流预测的研究中，牛娜通过分析区域物流发展与地方农业经济发展之间的关系，研究了区域物流合理化预测对地方农业经济发展的影响[3]。陈长英将传统的灰色预测模型和马尔可夫链相结合，通过建立改进的预测模型对广西物流需求进行了预测[4]。梁永年等通过相关系数发现惠州市GDP与综合货运量之间密切相关，分别运用线性回归法和弹性系数法对惠州市物流需求量进行预测[5]。黄凯和王健围绕生鲜农产品冷链物流需求分别采用GM1，1、BP神经网络和RBF神经网络方法来进行预测[6]。王佳颖等发现BP神经网络模型较强的泛化能力，在预测青岛港口物流需求时有良好的表现[7]。樊东方等为了应对现有中长期宏观物流量预测模型的局限性和对我国宏观物流量进行预测分析，提出基于pccsAMOPSO算法的多目标变权组合预测模型[8]。雷蕾等运用贵州省货运周转量数据在灰色GM1，1模型下进行了物流需求量预测[9]。冉茂亮等将集成经验模态分解（EEMD）、局部均值分解（LMD）、长短期记忆网络（LSTM）和局部误差校正（LEC）代入模型，在EEMD-LMD-LSTM-LEC模型下进行了物流预测[10]。

本文选取苏州市作为研究对象，基于GDP等重要经济指标，采用二次指数平滑法和回归分析预测法对苏州市综合货运量进行分析，将综合货运量的实际值和两种方法得到的预测值进行比较。通过对比两种方法的相对误差，选择相对误差较小的方法对未来三年苏州市综合货运量进行预测，以期为苏州市物流发展提供数据借鉴。

1  苏州市物流现状

苏州地处中国华东地区、江苏东南部、长三角中部，是扬子江城市群重要组成部分，东临上海、南接嘉兴、西抱太湖、北依长江。鉴于其优越的地理位置，苏州市一直是我国重要的物流转运中心城市之一。苏州是Adidas、黛珂、无印良品等大型企业仓储和快递转运的中心。双十一等大促期间苏州仓储经常出现的爆仓情况给许多快递企业、商家和消费者带来了困扰。因此，对苏州市物流货运量进行预测，可以帮助苏州市更好地制定相应的物流管理计划，更快速地应对突发的情况。

根据苏州市统计局2013年至2020年的统计年鉴和2021年苏州市统计公报，苏州市综合货运量的具体数据如表1所示，其中综合货运量由铁路货运量、公路货运量和水路货运量三部分组成。

由于物流需求量通常用综合货运量进行衡量，且经济发展与物流发展之间存在着一定关系，因此表2收集整理了综合货运量、GDP、第一产业、第二产业和第三产业的数据作为预测所需的基础数据。

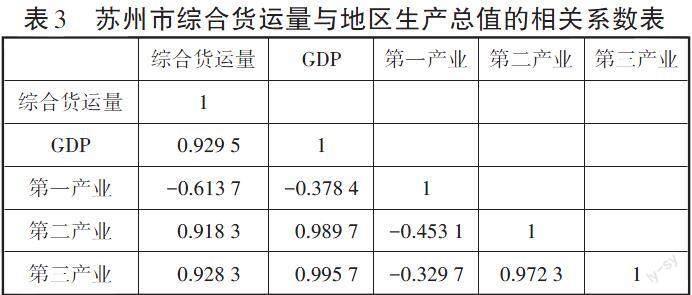
为更加直观地了解苏州市经济运行情况与综合货运量的关系，通过Excel表格软件的数据分析得到苏州市综合货运量与经济指标之间的关系[5]，如表3所示。

根据表3，与苏州市综合货运量密切相关的经济指标为GDP（0.929 5）、第二产业（0.918 3）和第三产业（0.928 3）。这说明GDP、第二产业和第三产业与综合货运量之间存在比较强的正相关关系，这些指标均可用于苏州市综合货运量的预测。由于GDP与综合货运量的相关性最强，因此采用GDP来预测苏州市的综合货运量。

2  苏州市物流需求预测建模

2.1  二次指数平滑法

指数平滑法是依托于移动平均法发展起来的，其实质上是一种特殊的加权移动平均法[11]。指数平滑法包括一次指数平滑法和二次指数平滑法等。由于一次指数平滑法不能进行有明显趋势波动的数据预测，且一次指数平滑法存在只能预测未来一期数据的缺陷，因此本文选择二次指数平滑法进行预测。

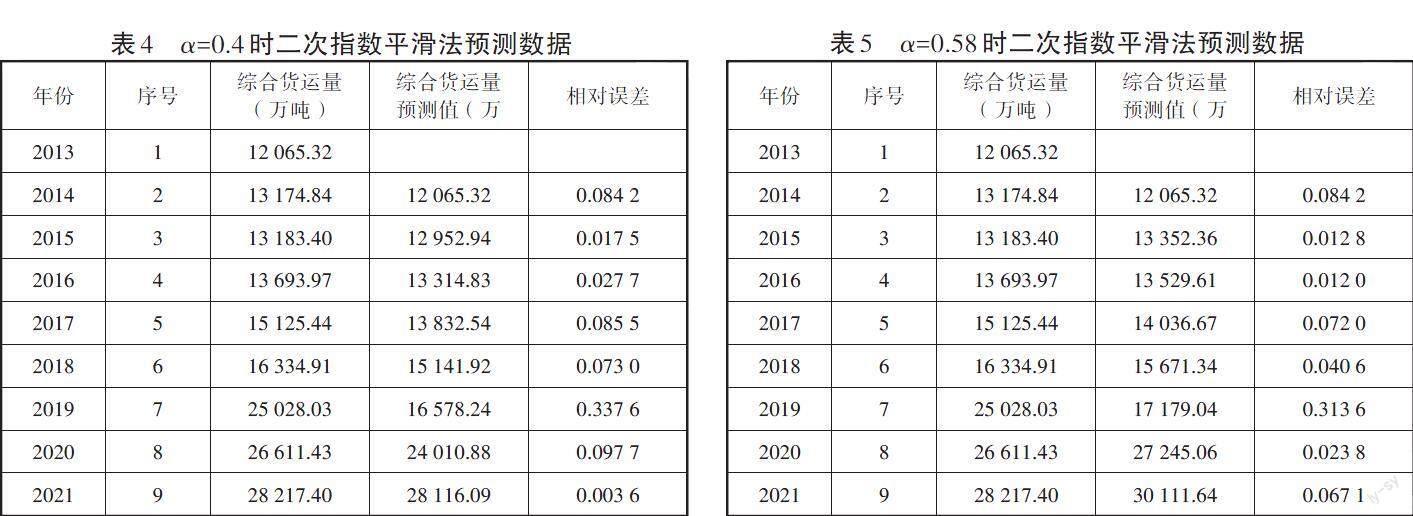
根据指数平滑系数α的选取原则，本文选取0.4作为α的值，将第一期的实际值（即2013年的综合货运量）作为第一次预測的初始值，根据二次指数平滑法的公式与计算步骤，将综合货运量的实际值、预测值和相对误差分别列于表4。

当α=0.4时，MSE（均方误差）为10 336 868.995。虽然表4中的相对误差较小，但本文在选取指数平滑系数α时具有一定的主观性。因此，为保证预测值的最优性，通过运用Excel表格软件中的模拟运算表，将0.01至0.99（α的精确度为小数点后两位）之间的所有数值分别作为指数平滑系数α进行模拟运算[12]，找到最优α值。通过计算发现当α=0.58时，其MSE最小，此时MSE*=8 563 586.2。鉴于此，运用最优指数平滑系数α=0.58再次进行预测，得到表5的数据。

将表4与表5中的相对误差进行对比，绘制图像如图1所示。观察该图可以发现，α=0.58时的相对误差大体上离轴更近，进一步验证了上文的结论（α=0.58是最优指数平滑系数）。

2.2  回归分析预测法

回归分析预测法依托于自变量与因变量之间的关系，是通过建立变量之间的回归方程进行预测的。根据自变量与因变量的相关关系不同，回归分析预测法可分为线性回归预测和非线性回归预测[2]。回归分析预测法也是预测的一种重要方法，常常用于中短期数据的预测。具体步骤为：首先，根据预测目标，确定自变量与因变量；其次，建立回归预测模型，进行相关分析；再次，检验回归预测模型，计算出相对预测误差；最后，确定预测值[13]。

观察表2和表3，可以看出GDP与年份、综合货运量与GDP之间均存在正相关关系，因此本文将分别采取线性回归预测进行分析。

首先，通过建立GDP与年份关系的回归方程预测GDP的数值。将年份作为自变量x，GDP作为因变量y，通过SPSS进行线性回归分析，得到如图2所示的系数表格。根据图2可以看出，GDP与年份的回归方程为y=1 182.08x-2 367 155.08。

同时，绘制GDP与年份的散点图及回归方程，如图3所示。

与上文相同，再将GDP作为自变量y，综合货运量作为因变量z，进行线性回归分析，得到图4所示的系数表格。根据图4可以看出，综合货运量与GDP之间的回归方程为z=1.85y-13 496.43。

同理，根据综合货运量与GDP的关系绘制散点图和回归方程，如图5所示。

最后，在已知GDP与年份、综合货运量与GDP关系的回归方程之后，首先通过GDP与年份的回归方程y=1 182.08x-2 367 155.08计算GDP的预测值；再基于综合货运量与GDP之间的回归方程z=1.85y-13 496.43，将预测的GDP数据代入自变量中，计算出综合货运量的预测值，进一步得到综合货运量实际值与预测值之间的相对误差，如表6所示。

2.3  对比与预测分析

为找出二次指数平滑法和回归分析预测法二者中更优的预测方法，将表5与表6中的相对误差进行比较，通过运用相对误差较小的预测方法，确定2022年、2023年和2024年苏州市综合货运量的预测值。两种方法相对误差的比较如图6所示。

根据图6可以看出：

（1）二次指数平滑法的相对误差总体上比回归分析预测法的相对误差小。

（2）二次指数平滑法下预测值更接近于实际值。

因此，根据二次指数平滑法的公式Y■=a■+b■T进行2022年、2023年和2024年综合货运量预测，其中a■和b■为2021年预测过程中的计算结果，且a■=28 551.54，b■=2 751.21。具体预测值如表7所示。

3  苏州市物流业发展建议

虽然苏州市物流管理已经有一套相对完备的系统，但其仍可以从以下两个方面进行改进：

（1）完善物流运输流程。由于大部分物流运输业务均通过公路运输完成，因此苏州市可以在大促期间简化物流运输流程，开设快递专用高速通道。这种举措不仅可以提高快递运输效率，还可以在一定程度上增加单位货运量，吸引更多的电商在此建立仓库，从而加快苏州市经济发展的步伐。

（2）合理规划物流路线，建立物流园区。根据预测，苏州市未来三年的综合货运量呈逐年递增的趋势。通过对物流路径的优化既可以节省运输时间，又可以缓解城市交通拥挤的问题。对物流运输车辆的时间限制也可以起到相同的作用。同时，苏州市还可以将较小的临近物流园区重新规划，组建成一个较大的综合物流园。这样做既推动了城市的进一步规划，又在一定程度上满足了物流企业周转的需求。

4  结  论

物流与经济之间不可分割的关系表明物流发展可以带动经济发展。物流需求作为衡量物流发展水平的主要指标，对了解经济发展情况也有重要的参考作用。物流需求的预测可以帮助企业和政府提前制定相应的对策以应对突发情况。本文考虑重要经济指标，通过运用二次指数平滑法和回归分析预测法对苏州市的综合货运量进行分析，发现二次指数平滑法下的综合货运量预测值更接近于真实值，在二次指数平滑法下通过预测发现2022年、2023年和2024年的综合货运量预测值分别为31 302.76万吨、34 053.97万吨和36 805.18万吨。基于上述分析，苏州市可以通过进一步完善物流运输流程、优化物流路径和建立综合物流园区的方法更好地发展苏州市的物流业。

参考文献：

[1] 孙明贵. 物流管理学[M]. 北京：北京大学出版社，2002.

[2] 王长琼. 物流系统工程[M]. 北京：高等教育出版社，2007.

[3] 牛娜. 区域物流需求合理化預测与我国农业经济发展格局关系研究[J]. 农业经济，2019（3）：139-141.

[4] 陈长英. 基于改进的灰色-马尔可夫链模型的广西物流需求预测研究[J]. 西部交通科技，2019（10）：152-155.

[5] 梁永年，姚镇城，蒋文博，等. 惠州物流需求预测研究——兼论惠州市综合运输体系建设[J]. 物流工程与管理，2020，42（7）：36-39.

[6] 黄凯，王健. 我国生鲜农产品冷链物流需求预测分析：基于最优组合模型[J]. 武汉理工大学学报（信息与管理工程版），2020，42（6）：524-529.

[7] 王佳颖，顼玉卿，李媛. 基于神经网络的青岛港口物流需求量预测研究[J]. 青岛职业技术学院学报，2021，34（6）：70-76.

[8] 樊东方，罗凯，靳志宏. 基于pccsAMOPSO的宏观物流量多目标变权组合预测模型[J]. 大连海事大学学报，2021，47（4）：19-29.

[9] 雷蕾，吴洁，陈嘉星. 基于灰色GM1，1的贵州物流需求“十四五”预测分析[J]. 枣庄学院学报，2022，39（5）：78-84.

[10] 冉茂亮，陈彦如，杨新彪. 基于EEMD-LMD-LSTM-LEC深度学习模型的短时物流需求预测[J]. 控制与决策，2022，37（10）：2513-2523.

[11] 张雪琴. 关于“指数平滑法”的研究[J]. 内蒙古农业大学学报（自然科学版），2006，27（4）：153-156.

[12] 蒋昌军. Excel环境下指数平滑预测法最优平滑系数的确定[J]. 中国管理信息化，2012，15（2）：13-15.

[13] 方威，肖衡，任湘郴. 基于线性回归模型的物流需求预测分析[J]. 生产力研究，2009（12）：94-95，110.