利用早停可微架构搜索的三维点云模型分类
张景发,杨 军,2
(1.兰州交通大学 电子与信息工程学院,兰州 730070;2.兰州交通大学 测绘与地理信息学院,兰州 730070)
0 引 言
三维模型识别与分类广泛应用于医学影像分析、自动驾驶、虚拟现实等领域,成为计算机视觉和计算机图形学等相关领域的重要研究课题。传统的三维模型识别方法利用人工设计特征描述符提取特征,如几何形状描述符[1]和热核签名描述符[2]等。由于人工设计的特征描述符良莠不齐,而且泛化能力较弱,研究人员提出利用深度学习提取特征描述符。基于深度学习的三维模型识别方法主要包括基于体素的方法[3]、基于多视图的方法[4]和基于点云表示的方法[5]。前2种方法需要将三维点云数据转换为体素网格或二维投影视图,这种数据形式的转换过程不仅会丢失特征信息,还会增加时间成本和内存开销。基于点云表示的方法不仅更加接近模型的原始表征,且可以将原始几何信息保留在3D空间中,不会进行任何离散化,有利于端到端的学习,因此,基于点云表示的方法成为了三维模型识别的主流方法。文献[5]提出的深度学习网络框架PointNet,使用多层感知机(multilayer perceptron,MLP)与最大池化操作确保了点云输入的无序性,并利用T-net网络实现了数据及特征的有效对齐,在点云模型的识别上做出了开创性工作。然而,PointNet网络没有考虑到点与其周围的邻域信息,且未针对点云密度不均匀的特点进行特殊设计。文献[6]对上述问题做出了改进,提出了PointNet++,通过在网络中分层使用PointNet,并将PointNet网络应用于局部区域,生成区域的特征向量。该算法不仅解决了采样不均匀的问题,也考虑到了空间中点与点之间的距离度量问题。文献[7]提出了边缘卷积(edge convolution,EdgeConv)模型,在三维空间中找出与输入点相近的k个最近邻点,并使用这些点与其中心点的曼哈顿距离构造邻域特征。该方法不仅可获得局部邻域信息,而且通过堆叠边缘模块,可以提取到全局形状信息。
基于深度学习的方法在三维模型识别领域已经取得了显著的成果,但其所使用的网络架构大多由人工构建,网络架构设计过程严重依赖专家经验,且需要耗费大量的时间和人力成本。因此,基于深度学习的三维模型识别方法面临的主要挑战是设计高效且普适的网络架构。随着神经架构搜索(neural architecture search,NAS)[8]的提出,研究者逐渐将NAS方法应用到模型识别与分类任务中。NAS利用一个循环神经网络作为控制器,通过强化学习方法来搜索子网络,不断更新控制器的参数,直至搜索到符合要求的网络。搜索到的网络在性能方面达到了人工设计网络的准确度,其缺点在于耗费了大量计算资源,即使对CIFAR-10这样的小型数据集,也需要数百个GPU训练一天时间。为了解决这个问题,文献[9]提出了基于cell结构的搜索空间,将cell结构表示为一个内部有多个节点的有向无环图,其中每个节点表示网络提取的特征图,节点之间的有向连接表示预定义的各种候选操作,通过搜索具有各种拓扑方式的cell结构并将搜索到的cell结构重复堆叠,得到最优的网络架构。此方法成功将NAS搜索时间缩短到1/1000以下。文献[10]在基于cell结构搜索空间的基础上提出了DARTS算法,利用Softmax函数将搜索空间从离散松弛状态转化为连续状态,使得目标函数可微。在搜索时,DARTS会遍历全部节点,使用节点上候选操作的权重进行计算,同时优化架构参数和网络参数。搜索结束后,在各节点之间选择权重最大的候选操作,构建完整的网络架构。
本文提出早停可微架构搜索(early-stopping differentiable architecture search,ES-DARTS)算法,主要创新点和贡献有:①解决了人工设计网络费时费力又容易出现错误的问题,并在性能上超越了人工设计网络;②设计了适用于三维点云模型的搜索空间,提高了网络架构的搜索效率;③通过追踪搜索空间中候选操作的权重变化,在跳跃连接发挥不公平竞争的临界点停止搜索,解决了基于DARTS算法自动搜索网络架构易出现性能崩溃的问题。
1 早停可微架构搜索
1.1 搜索空间
对于二维图像识别任务,NAS已经有了许多定义明确的搜索空间;而对于三维点云数据,由于其与二维图像数据格式不同,因而这些搜索空间中的候选操作不能直接应用。本文在一些主流三维模型识别与分类网络基础上,针对三维点云数据的特点设计了新搜索空间,利用专家设计网络模型中的先验知识,预定义一个包含高效候选操作的搜索空间,有助于ES-DARTS算法搜索到最优的网络架构;同时,为了降低网络模型的复杂性,在搜索空间中设计了一些轻量级的候选操作,如Local conv和Group conv[11]等,可大大提高搜索效率,在性能和搜索成本之间取得平衡。
本文搜索空间包含多种候选操作,Skip Connection操作的作用与ResNet[12]相同,可防止在较深的网络中出现梯度消失。Conv_1×1操作对卷积神经网络进行降维,并在不改变特征图的前提下,实现各通道之间的线性组合。Local conv操作可以有效聚合邻域点的特征、邻域点与采样点的边特征,充分挖掘局部几何特征,使每个采样点的特征更加丰富。GCN[13]解决了卷积神经网络无法有效处理非欧几里得数据的问题。Gat方法[14]采用跨节点对并行,能高效地为邻域中的不同节点指定不同权重,且不需要代价高昂的矩阵运算。Group conv通过将同一卷积层中的卷积核分成不同的小组,解决了随着卷积网络中卷积核个数增多时出现的卷积冗余问题,在保持模型精度的同时减少参数量和计算量。文献[15]认为图神经网络具有同构性,即对同构图处理后的特征应该相同,对非同构图处理后的特征应该不同,引入一个可学习参数对点的原始特征进行映射,并将映射后的特征同邻域特征进行聚合。文献[16]提出的GraphSAGE是一种节点表示方法,通过从一个顶点的局部领域点采样并聚合节点特征信息,可以有效地为其他顶点生成嵌入图特征映射,而不需要对每一个顶点单独进行训练,提高了训练效率。
1.2 可微神经架构搜索
本文cell结构如图1所示。cell结构由6个节点的有向无环图(direct acyclic graph,DAG)组成,包括2个输入节点、3个中间节点和1个输出节点。节点代表了网络的特征映射,节点之间的有向连接表示各种操作的选择。图1中,输入节点是前2个cell结构的输出表示,中间节点聚合来自其所有前置节点的信息流,输出节点被定义为固定数量的前置节点的串联,从节点i到j的边ei,j表示对输入特征xi进行操作选择,并且其输出xj被表示为oi,j(xi)之和,即

图1 cell结构Fig.1 Cell structure
(1)
搜索空间中的元素是cell结构中各节点之间的候选操作集合。cell结构的部分简化构建过程如图2所示。图2a是未进行架构搜索时的cell结构,“?”表示待处理;图2b是通过Softmax函数松弛化搜索空间,使搜索空间从离散变为连续,从而将各节点之间的操作选择表示为一个混合操作;图2c以线条的粗细表示各节点对标候选操作的权重大小;图2d选择各节点对标权重占比最高的候选操作,获得完整的cell结构。

图2 cell结构的部分简化构建过程Fig.2 Partial simplification of the construction process of cell structure
cell结构利用Softmax函数计算各节点之间混合操作的权重占比,并选择各节点对中权重占比最高的候选操作作为最终输出,表示为
(2)

(3)
(3)式中,Ltrain和Lval分别表示训练和验证损失,其大小由体系结构α与候选操作权重ω共同确定。算法的目标是找到使验证损失Lval(ω*(α),α)最小的体系结构α,与搜索到的体系结构α相对应的权重ω*是通过最小化训练损失得到的。
1.3 早停策略
DARTS算法的核心任务是优化体系结构参数α和模型权重参数ω,这2个参数是交替进行优化的。然而,在优化过程中,DARTS算法自动搜索到的网络会出现性能崩溃现象,即随着搜索过程中迭代次数的增加,网络的性能不但不会一直提升,反而可能出现下降。DARTS算法之所以出现性能崩溃,是因为其在使用Softmax函数松弛化搜索空间时,将任意2个节点之间的各种候选操作加权为一个混合操作权重,各操作之间存在一种排他性竞争,一种候选操作权重的提升,会抑制其他操作的权重[17]。在搜索空间中定义的跳跃连接操作,虽然可以防止网络层数过深而导致梯度爆炸,但由于其与卷积的结合比较好,跳跃连接操作在网络搜索过程中会逐渐占据主导地位,在排他性竞争中严重削弱了其他操作的权重,导致搜索到的cell结构中存在太多跳跃连接,使网络崩溃。这种现象被定义为不公平竞争,他促使跳跃连接在排他性竞争中占据垄断地位。
在双重优化算法中,体系结构参数α和模型权重参数ω是先合作后竞争的关系。开始搜索cell结构时,这2个参数相互促进,此时是合作关系;经过多次迭代之后,由于模型权重在竞争中比架构参数更具优势(如模型权重的数量远远大于架构参数的数量,架构参数在双重优化中对最终损失不敏感等),他们逐渐转向相互竞争的关系,导致搜索到的体系结构性能先上升后下降。
为了解决跳跃连接不公平竞争问题,本文通过追踪网络搜索过程中各候选操作的权重变化,并在其出现明显变化时停止搜索,即寻找双重优化过程中架构参数和模型权重参数合作与竞争之间的临界点。在此临界点之前,跳跃连接对网络性能起着促进作用,超过这个临界点,就会阻碍网络性能。临界点选取可以表示为
(4)
(4)式中:ωn表示第n次迭代时的候选操作权重大小;ωn-k表示在n周围k个迭代上的候选操作权重大小;h为停止条件的阈值。当某个候选操作的权重变化超过阈值h时,则在第n-k次迭代处停止搜索,以找到性能最优的网络架构。将此方法与其他的早停策略进行实验对比,结果表明,本文所提出的早停策略不仅可以打破这种不公平的竞争,而且还取得了比直接限制跳跃连接数量更好的效果。
2 实验结果与分析
本文在ModelNet10和ModelNet40这2个标准公开数据集上进行了实验。ModelNet10包含4 899个三维模型,分为10个不同的类别。ModelNet40数据集有40个类别,包含12 311个三维模型,其中,9 843个为训练模型,2 468个为测试模型。
2.1 网络架构搜索
使用ModelNet10数据集搜索cell架构,采用与DARTS相同的搜索策略,cell结构由6个节点组成,分为2个输入节点,3个中间节点及1个输出节点。第1和第2输入节点分别为前2个cell结构的输出,输出节点是所有中间节点的深度级联。搜索到最优cell结构之后,通过将cell结构堆叠2次并在ModelNet10上构建最终的网络架构。考虑到神经架构搜索的随机性,本文进行了5次独立搜索,得到了5个不同的最优cell结构,如图3所示。

图3 5次独立搜索得到的不同cell结构Fig.3 Different cell structures obtained from 5 independent searches
参数设置:从ModelNet10中的每个三维模型中采样1 024个点,输入特征维度为3,分别用x、y和z坐标表示。对于体系结构参数α和模型权重ω,本文遵循同DARTS[13]同样的设置,使用初始学习率为3×10-4、动量为0.5和权重衰减为10-3的Adam优化器进行优化。为防止架构搜索过程出现梯度爆炸,在每个节点处都采用批量归一化。
2.2 网络架构评估
在搜索阶段搜索到最优cell结构之后,通过将最优cell结构多次堆叠来构建更大的网络体系结构。由于ModelNet40与ModelNet10数据集大小不同,因此所需的网络深度也不一样。在ModelNet40数据集,将搜索到的cell结构堆叠3次,特征通道大小为128,优化器的选择同ModelNet10相同。网络架构评估过程中会随机初始化网络的权重(丢弃在搜索过程中学习到的权重),重新训练网络架构,并在测试集上测试此网络的性能。此阶段设置迭代次数为400,以使网络趋于收敛。
实验中运行了5次独立搜索,得到了5个不同的体系结构。在ModelNet40数据集上对这5个不同体系结构进行性能评估,并给出每次评估的总体识别准确率和参数大小,实验结果如表1所示。

表1 5次独立搜索体系结构的准确率Tab.1 Accuracy of five independent search architectures
搜索到的网络架构在ModelNet40数据集上最高达到了93.2%的识别准确率,由于每次独立搜索到网络架构中候选操作的不同,其参数大小也有所差异,其中跳跃连接操作的参数计算最少,包含跳跃连接的网络架构中的参数量明显少于其他网络。
ES-DARTS搜索到的体系结构与主流的人工设计网络对比结果如表2所示。表2中,搜索耗时针对非人工方式。

表2 不同算法在ModelNet40的识别准确率对比Tab.2 Comparison of recognition accuracy of different algorithms on ModelNet40
由表2可以看出,使用NAS算法自动搜索出的网络架构取得了比人工设计网络更好的识别准确率。图4是模型识别准确率随着迭代次数的变化情况。从图4可以看出,在训练初期,随着迭代次数的增加,识别准确率逐渐提高,当迭代次数达到220次时,网络趋于收敛,故基于神经架构搜索策略自动构建网络对于三维模型分类任务是有效的。

图4 迭代次数与模型识别准确率的统计结果Fig.4 Statistical results of the epoch and model recognition accuracy
2.3 早停实验
本实验通过追踪网络搜索过程中各种候选操作的权重变化,找到双重优化过程中架构参数和模型权重参数合作与竞争之间的临界点,以解决跳跃连接的不公平竞争。设置网络搜索过程迭代次数为50,由于搜索空间中定义了9种候选操作,因此,追踪50次迭代过程中各节点间9种候选操作的权重变化。为了确定阈值h的取值大小,在保持其他参数不变的情况下对h的取值进行多次实验,确定最佳参数设置。表3显示了当阈值h取不同值时搜索到的网络识别准确率。从表3可以看出,当h取值0.1和0.4时,识别准确率较低;取0.2时,识别准确率高于其他取值。因此,本文将阈值h取值设置为0.2。本文也展示了一组中间节点对之间各候选操作的变化情况。除跳跃连接之外的其余候选操作在50次迭代中的权重变化都比较小,跳跃连接操作在搜索阶段刚开始时是稳定变化的,而在迭代一定次数之后,其权重发生明显变化。cell结构各候选操作权重竞争过程如图5所示。本文方法可以简单而直观地找出跳跃连接操作发挥不公平竞争的临界点,在该临界点之后,跳跃连接开始抑制其他操作的权重,使搜索到的网络性能不佳,在此临界点处停止搜索,进而获得性能最优的cell结构。
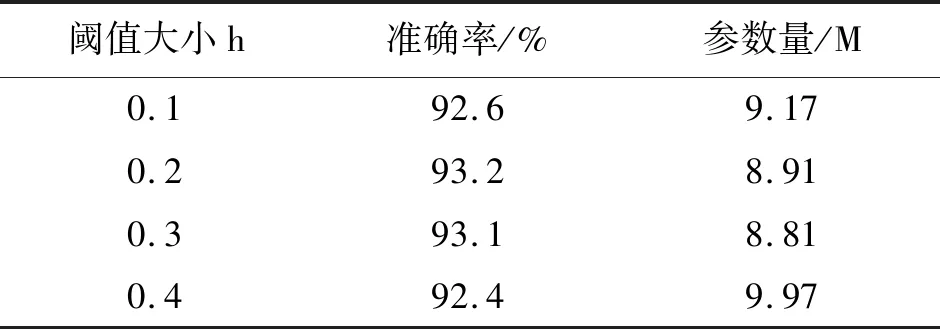
表3 不同阈值识别准确率的比较Tab.3 Comparison of recognition accuracy with different thresholds

图5 cell结构各候选操作权重竞争过程Fig.5 Competition process of each candidate operation weight of the cell structure
为了证明有效性,将本文与P-DARTS[26]、FairDARTS[17]、DSNAS[27]等算法中的早停策略进行实验对比。P-DARTS通过在跳跃连接之后使用dropout,在优化过程中限制跳跃连接的数量。FairDARTS通过在架构参数上应用Sigmoid代替Softmax,允许每个候选操作具有独立的体系结构权重,以避免排他性竞争,打破跳跃连接导致的不公平竞争。DSNAS采用了渐进式提前停止策略,为停止条件设置阈值,一旦任何边或层满足此条件,就直接选择此时权重最高的候选操作,停止优化,并在随后的训练中更新体系结构参数。这些方法都应用于二维图像ImageNet数据集,本文根据论文作者所公开的代码在Modelnet40数据集上进行了复现。不同算法中早停策略的比较如表4所示。由表4可以看出,本文早停策略取得了优于其他几种算法的识别准确率,这是由于其他几种算法主要是针对于二维图像进行设计的,没有考虑到三维点云模型的特点。此外,本文早停策略找出了跳跃连接操作发挥不公平竞争的临界点,在网络还没有完全收敛时就停止搜索,因此在搜索时间上也取得了更优的结果。

表4 不同算法中早停策略的比较Tab.4 Comparison of early stopping strategies in different algorithms
2.4 消融实验
为了验证本文早停策略能够有效解决跳跃连接的不公平竞争,设置了3种不同的搜索方法进行对比实验:不使用早停搜索50次(S1)、不使用早停搜索200次(S2)、使用本文的早停设置(S3),实验结果如表5所示。由表5可以看出,在相同的搜索空间条件下,S2方法搜索到的网络架构性能最差,明显出现了性能崩溃的现象;S1方法只比S3的性能低0.3%,这是因为将搜索次数设置为50次,实质上是一种隐含的早停策略,由于没有在跳跃连接开始发挥不公平竞争的临界点处停止搜索,因此其识别准确率不如S3方法。S1、S2、S3这3种搜索方式的cell结构如图6所示。由图6可以看出,S2方法由于没有使用早停策略来限制跳跃连接操作的不公平竞争,导致所搜索到的cell结构中存在3个跳跃连接,使得网络层数太浅,出现网络性能崩溃。而S1和S3方法中的跳跃连接个数都为1个,对网络的性能影响不大。

表5 3种不同搜索方式的准确率Tab.5 Accuracy of three different search methods

图6 S1、S2、S3 3种搜索方式的cell结构Fig.6 Cell structure of S1,S2,and S3 search methods
为了更好地分析跳跃连接操作对网络架构性能的影响,本文设置了2个搜索空间,一个搜索空间中包含跳跃连接操作,另一个搜索空间中不包含跳跃连接操作,其他设置完全相同。跳跃连接对搜索空间的影响如表6所示。由表6可知,包含跳跃连接搜索空间搜索到的网络识别准确率比较高,表明适当数量的跳跃连接确实有利于网络的性能提升。因此,对于跳跃连接的不公平竞争,只能对其进行限制,而不能直接舍弃。

表6 跳跃连接对搜索空间的影响Tab.6 Impact of skip connections on the search space
为了验证本文设计搜索空间的高效性,采用随机搜索进行实验对比。在搜索空间中随机搜索10组cell结构,由于随机搜索具有不确定性,这10组cell结构各自构建的网络性能差别较大。本文首先在Modelnet10数据集上对这10组网络架构分别进行5个迭代的训练,然后根据实验结果选择验证准确率最高的一组网络架构,最后在与ES-DARTS相同的设置下在Modelnet40数据集上进行训练和测试,识别准确率实验结果体现在表2中。由表2可以看出,采用随机搜索算法搜索到网络架构的识别准确率只比ES-DARTS算法的平均识别准确率低2%,说明对于NAS方法,设计一个优越的搜索空间是至关重要的。图7为随机搜索到的最优cell结构,各节点间候选操作同ES-DARTS算法所选择出的候选操作差异比较大,但其性能却比较接近,证明了本文所设计搜索空间的高效性。

图7 随机搜索的cell结构Fig.7 Random search cell structure
3 结束语
现有的三维模型分类网络架构大多采用人工设计,设计过程很大程度依赖于专家经验,费时费力,且构建的网络性能良莠不齐。本文在DARTS算法的基础上,提出一种自动搜索三维模型分类网络架构的方法,针对三维点云模型的特点设计了新的搜索空间,以便自动搜索到性能优于人工设计的网络架构;对于DARTS算法中存在的跳跃连接操作所导致的不公平竞争,提出了追踪各候选操作权重大小的方法,通过在跳跃连接权重明显增大时停止搜索,以解决跳跃连接的不公平竞争现象。实验结果表明,本文提出的方法能够有效地搜索出适合三维模型分类任务的网络架构,并在ModelNet40数据集上达到了93.2%的识别准确率,高于人工设计的网络。

