一种适用于伪码连续波雷达的测量波动优化方法
郭东文,吴爽,崔嵬
(北京理工大学 信息与电子学院,北京 100081)
为适应空间对接过程中远、中、近不同距离的测量需求,一般综合采用微波雷达、激光雷达、CCD相机等交会测量设备接力完成不同距离下的测量.交会对接微波雷达测量系统主要作用与远程引导段和辅助近程引导段,常用的微波雷达测量方式主要有脉冲测量、侧音测量和伪码连续波测量3 种[1−2].脉冲雷达测量体制有分辨率低、易受空间目标干扰的缺点;侧音测量体制虽然测量精度较高,但很难实现远距离测距.伪码连续波测量具有测量距离远、测量精度高、抗干扰能力强、可与通信链路复用等特点,而被广泛应用于空间交会对接微波雷达测量系统[3].
对于伪码连续波雷达测量系统,若采用单向测量方式,由于收发两端使用的时钟频率非相参,影响雷达测量系统的测量精度.为了克服收发两端时钟非相参带来的影响[4],采用主动应答式双向测量体制,两个目标终端分别安装雷达和应答机,应答机接收雷达发射信号并完成相干转发[5],雷达接收相干转发信号完成测距、测速、测角等测量功能.
尽管主动应答式双向测量体制可以消除雷达和应答机采用非相参时钟引入的测量误差[6−7],然而,由于雷达和应答机间的时钟为准同步,即不能完全相同,存在微小偏差.对于常用的雷达测量系统,采样偏差导致的测量误差可以忽略不计,但对于应用空间交会对接的高精度测量系统,采样偏差导致的测量误差不能忽略,需要进行详细分析并给出有效的优化方法.
综上所述,基于空间交会对接的实际应用需求,本文对伪码连续波主动应答式双向测量系统数字采样偏差引入的测量误差进行详细分析,并提出一种有效的优化方法.
1 伪码连续波主动应答式双向测量系统工作原理
伪码连续波主动应答式双向测量系统主要由微波雷达和微波应答机组成.微波雷达由雷达二次电源、雷达中频信号处理单元、雷达射频组合和雷达天线4 个模块组成;微波应答机由应答机二次电源、应答机中频信号处理单元、应答机射频组合和应答机天线4 个模块组成.图1 给出了伪码连续波主动应答式双向测量系统的大致工作流程.

图1 伪码连续波测量雷达系统Fig.1 Pseudocode continuous wave measurement radar system
雷达以fs_rd的采样时钟生成测距伪码,以BPSK方式调制在雷达的载波信号上,雷达发射信号Sup(t)为

雷达发射信号通过雷达天线向外辐射,应答机接收雷达射频载波信号,接收信号SR(t)为
式中,AR为 应答机接收信号的幅度;R为雷达与应答机之间的径向距离;c为真空中的光速;ϕR为应答机接收信号的初始相位;nR(t)为噪声.
则应答机接收信号频率fR_rsp为

同理得到应答机接收的伪码频率fcR_rsp为
应答机接收信号经过两次下变频并通过采样率为frsp的A/D 进行带通欠采样,得到数字中频信号Szp(k/frsp)为[8]
式中:Azp为 数字中频信号的幅度;ϕzp为数字中频信号的初始相位;nzp(k/frsp)为 噪声;∆f=frd−frsp.
对式(5)所示的中频信号通过捕获实现伪码相位延迟和载波频率粗测量[9-10],然后通过跟踪环路实现伪码相位延迟和载波频率的精细测量[11].应答机在完成伪码、载波信号的跟踪处理基础上,进行伪码和中频载波信号的相干转发.

式中:round[·]表 示四舍五入取整;fs为雷达和应答机晶振的标称频率;L为应答机发射信号基于晶振频率的 倍 频 数,L/M为 转 发 比;Nf为 载 波NCO 寄 存 器 的位数,载波NCO 最低分辨率fs/2Nf≪1.
由于应答机载波NCO 的工作频率为frsp,则根据式(6)得到应答机转发中频频率[12−13]fTzp_f为

应答机数字转发中频载波信号经过D/A、上变频得到应答机转发载波信号,频率为
式中:fdown为应答机发射频率,fdown=L×frd.
式中:Adown_f为转发载波信号幅度;ϕdown_f为转发载波信号初始相位.
与转发中频信号相似,转发伪码的FCWTc[14]为

根据式(10)得到应答机转发伪码的频率fc_down为
从式(11)可以得出,应答机转发伪码频率fc_down已完成伪码相干转发处理,再加上捕获跟踪得到的伪码相位,生成转发伪码信号电平Pdown(t)输出,与转发载波信号经过BPSK 调制,得到应答机转发信号Sdown(t)为
式中:Adown为应答机转发信号幅度;ϕdown为应答机转发信号初始相位.
微波雷达接收应答机的转发信号,与微波应答机接收微波雷达的工作流程相似,通过下变频得到频率为 5frd/4+fd_rd的 中频信号,经过采样率为frd的AD带通采样,得到频率为frd/4+fd_rd的数字中频信号,经过工作频率为frd的数字信号处理,捕获跟踪得到码相位延迟和多普勒频率,最终解算得到雷达相对于应答机的径向距离和径向速度.
2 数字采样时钟偏差对测量精度的影响及优化方法
由于雷达和应答机的采样时钟不完全相同,存在微小偏差,因此本文详细分析雷达和应答机数字采样时钟偏差对测量系统测量精度的影响.
假设在静态条件下,应答机的转发伪码频率为fc_rd,雷达的接收伪码频率也为fc_rd.应答机以采样率frsp再生频率为fc_rd的转发伪码信号,雷达以采样率frd对接收到的转发伪码信号进行采样,并通过再生频率为fc_rd的本地伪码完成接收信号跟踪测量.
对k个码片而言,雷达伪码采样频点数与雷达理想伪码采样频点数偏差[15−16]EFSk为
式中:floor[·]为向下取整;FCWc=round[(fc/fs)×2Nc]为雷达码频率字.
伪码采样频点数偏差反应在伪码NCO 工作过程中即为相位抖动,将其转化为码片偏差EFCk为
同理,对k个码片而言,应答机转发伪码采样频点数与雷达伪码采样频点数偏差EFS′k为
假设雷达、应答机标称时钟fs= 65.536 MHz,Ncs=62 500/8 191,雷达工作时钟为frd=fs+dfrd,应答机工作时钟为frsp=fs+dfrsp,雷达和应答机工作时钟钟差为df=dfrsp−dfrd.图2 和图3 分别给出了不同的码片数下,雷达伪码、应答机转发伪码采样频点数偏差以及码片偏差结果.

图2 伪码采样频点数偏差结果Fig.2 Results of the sampling point deviation for pseudocode

图3 码片偏差结果Fig.3 Results of chip deviation

图4 码相位跟踪结果Fig.4 Tracking results of code phase
由图2(a)和图3(a)可以看出,雷达伪码采样频点数偏差和雷达码片偏差呈现滞后,且偏差不大于1 个采样周期.由图2(b)和图3(b)可知,应答机转发采样频点数偏差和应答机转发码片偏差随钟差的不同呈现不同的周期性变化,偏差的最大值不大于1个采样周期,偏差变化周期为时钟偏差的倒数,即T∆=1/df.
相较于雷达的固定码片偏差,应答机相干转发引入的周期性偏差将导致雷达码环跟踪结果出现周期性波动,从而影响测量精度.由于应答机转发码片偏差的变化周期为T∆=1/df,则雷达码环跟踪结果的波动周期为T∆=1/df.

可以看出,雷达码相位跟踪结果呈现类正弦波周期波动,统计周期约为2.03 s,对应频率为0.49 Hz,与钟差0.5 Hz 基本一致,波动峰峰值幅度∆Rc约为0.129 chip,与1 个采样点对应的码相位fc/fs=0.131 chip,与分析的应答机转发码片偏差结果基本一致.
表1 给出了在不同的钟差df下,雷达跟踪码相位波动统计结果.

表1 码相位跟踪统计表Tab.1 Table of tracking code phase
从表1 可以看出码相位跟踪结果的误差频率约等于钟差,码相位的波动也随着钟差的增大而减小.
分析结果表明距离测量结果的误差波动与钟差有关,根据信号处理理论,通过设计合适的滤波器可消除频率误差的影响,本文在此基础上提出多级滤波的优化方法,即:在中频端口增加带通滤波器以及在伪码转发端口增加低通滤波器,从而减小钟差引入的周期性偏差,提高雷达测量精度.下面,通过仿真验证多级滤波优化算法的有效性.
当增加带宽为25 MHz 的中频带通滤波器后,图5给出了 df= 0.5 Hz 时增加中频带通滤波前后雷达码相位的跟踪结果.

图5 码相位跟踪结果(增加中频带通滤波)Fig.5 Tracking results of code phase (with IF bandpass filtering)
可以看出,经过中频带通滤波后,尽管码相位跟踪结果仍呈现周期波动,且波动频率与钟差基本一致.但波动峰峰值幅度 ∆Rc明显降低.
表2 给出了不同的钟差df下,增加中频滤波前后,雷达跟踪码相位波动对比结果.从表2 可以看出,经过中频带通滤波后,雷达和应答机钟差造成的波动峰峰值幅度 ∆Rc明显减弱,但该测量波动相对于最小距离可分辨率0.01 m(对应码相位0.000 5 chip)仍不可忽略.

表2 码相位跟踪统计表(增加中频带通滤波)Tab.2 Table of tracking code phase (with IF bandpass filtering)
为了进一步抑制距离波动,在转发伪码通路上增加一个10 MHz 的低通滤波器,图6 给出了钟差df为0.5 Hz 时码相位跟踪结果.

图6 码相位跟踪结果(增加伪码低通滤波)Fig.6 Tracking results of code phase (with pseudocode lowpass filtering)
从图6 可以看出,在中频带通滤波基础上增加转发伪码低通滤波,码相位跟踪波动峰峰值幅度∆Rc进一步降低.
表3 给出了不同的钟差df下,增加转发伪码低通滤波前后,雷达跟踪码相位波动对比结果.从表3可以看出,在中频滤波基础上增加转发伪码低通滤波后,当钟差大于2 Hz 时,测量波动峰值影响(峰峰值一半)相较于最小距离可分辨率0.01 m(对应码相位0.000 5 chip)可忽略不计.

表3 码相位跟踪统计表(增加伪码低通滤波)Tab.3 Table of tracking code phase (with pseudocode lowpass filtering)
3 实测验证
将两套微波雷达和微波应答机在暗室进行测试,设置雷达、应答机保持相对静止,设置雷达发射信号衰减0 dB(相当于雷达与应答机间相距1 000 m)
所选用的第一套微波雷达和微波应答机时钟钟差df为0.45 Hz,图8 给出了实测码相位跟踪结果.
由图7 可以看出,码相位实测跟踪结果呈现类正弦波周期波动,统计波动周期约为2.19 s,对应频率为0.46 Hz,波动峰峰值幅度 ∆Rc为0.006 chip.
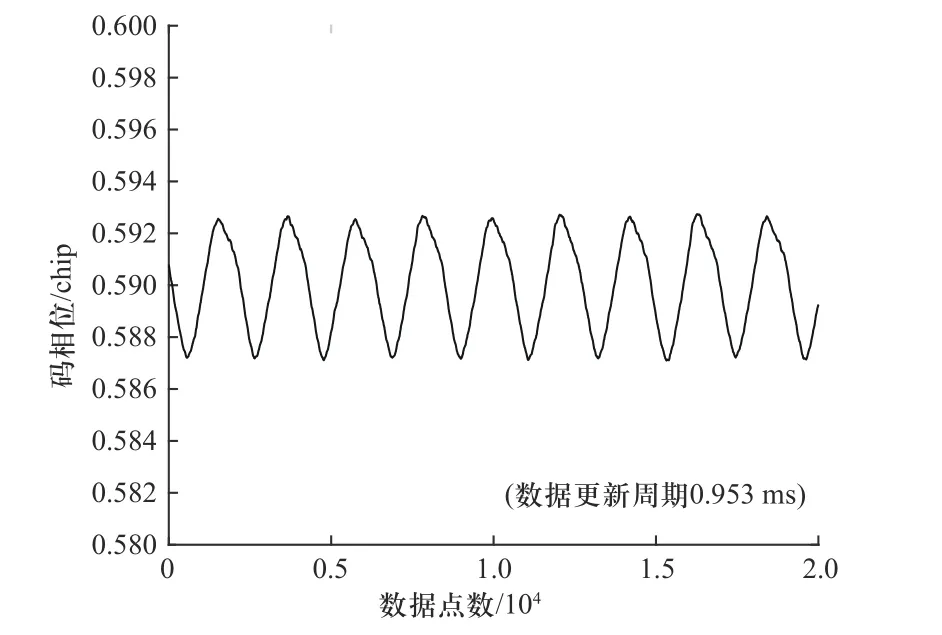
图7 微波雷达实测码相位跟踪结果(df = 0.45 Hz)Fig.7 Experimental results of tracking code phase with real radar data (df =0.45 Hz)
所选用的第二套微波雷达和微波应答机时钟钟差df为4.6 Hz,图8 给出了实测码相位跟踪结果.

图8 微波雷达实测码相位跟踪结果(df = 4.6 Hz)Fig.8 Experimental results of tracking code phase with real radar data (df =4.6 Hz)
由图8 可以看出,码相位实测跟踪结果呈现类正弦波周期波动,波动周期约为0.216 s,对应频率为4.63 Hz,波动峰峰值幅度 ∆Rc为0.000 4 chip,测量波动影响相较于最小距离可分辨率0.01 m(对应码相位0.000 5 chip)可忽略不计.
结合图7、图8 测试结果可以看出,实测结果与经过中频滤波和转发伪码滤波的仿真结果基本一致,其中波动峰峰值幅度有差别的原因是各套应答机转发伪码传输通道器件个体差异性导致的转发伪码低通滤波性能不一,所以在转发伪码信号通路上增加一个接近码速率但又不小于码速率的低通滤波器,可抑制微波雷达由钟差导致的周期性距离波动.
4 结束语
面向空间交会对接任务中高精密测量需求,在介绍主动应答式双向测量原理基础上,分析了实际工程应用中由于雷达和应答机间采样时钟为准同频,微小的频率偏差导致伪码跟踪结果周期性波动问题,并从工程实现的角度提出了通过多级滤波优化周期性测距误差的方法.仿真数据说明通过多级滤波后,距离波动的峰值可减小两个数量级,当钟差大于环路带宽时,测量波动影响相较于最小距离可分辨率可忽略不计,实现了最小代价下测量性能的有效优化,适用于现有交会对接测量系统的优化升级.最后通过暗室实际数据测试进一步验证了优化方法的有效性.

