基于卡尔曼滤波的UWB室内精确定位研究

张敏 杨瑞 管艳

摘要：高精度的定位系统对促进数字化时代的发展尤为重要。文章针对室内复杂环境的定位问题，建立基于线性卡尔曼滤波的定位模型，有望提高室内定位的精确度。文章首先根据UWB原理，利用三边定位法计算靶点坐标。其次使用卡尔曼滤波算法对坐标数据进行平滑处理，以减小因干扰信号引起的数据误差。最后模拟室内静态实验得到10组滤波前后的靶点坐标及其误差值。结果表明，本研究的定位模型明显提高了定位精度，对复杂环境下的定位具有一定的应用价值。

关键词：室内定位：卡尔曼滤波：UWB;复杂环境

中图分类号：TN92 文献标志码：A

0 引言

大数据时代背景下，万事万物都向着智能化方向发展。人们对定位技术的准确性和稳定性的要求也越来越高，因此研究高精度的定位系统显得尤为重要。现有的国内外定位系统以卫星定位为主，这类系统虽然在导航的使用领域和室外定位的应用十分广泛。但由于复杂区域的信号受阻，使得其在室内的定位精度并不理想，故无法满足人们对复杂区域高精度定位的需求[1]。随着技术的更新迭代，诸如红外线、超声波等定位技术相继出现。但其在定位精度或是系统功耗方面仍有缺陷。

超宽带（ UWB）是一种短距离高速无线通信技术。其具有对信号衰落不敏感、安全性高、系统复杂度低及定位精度高等特点[2]。UWB技术可以与现有的无线通信系统做到频率资源共享，进而提高频谱利用率，实现高速率通信。然而UWB存在许多干扰问题，例如，与现有无线通信系统因频谱重叠导致干扰、多径干扰及UWB系统相互干扰，这已然成为制约UWB技术发展的重要因素。针对此类问题，本文提出一种基于卡尔曼滤波的UWB定位模型。该模型主要用于解决UWB中因各类干扰引起的定位误差大和定位点漂移等问题，从而实现高精度定位。

1 定位原理及方法

1.1

UWB定位原理

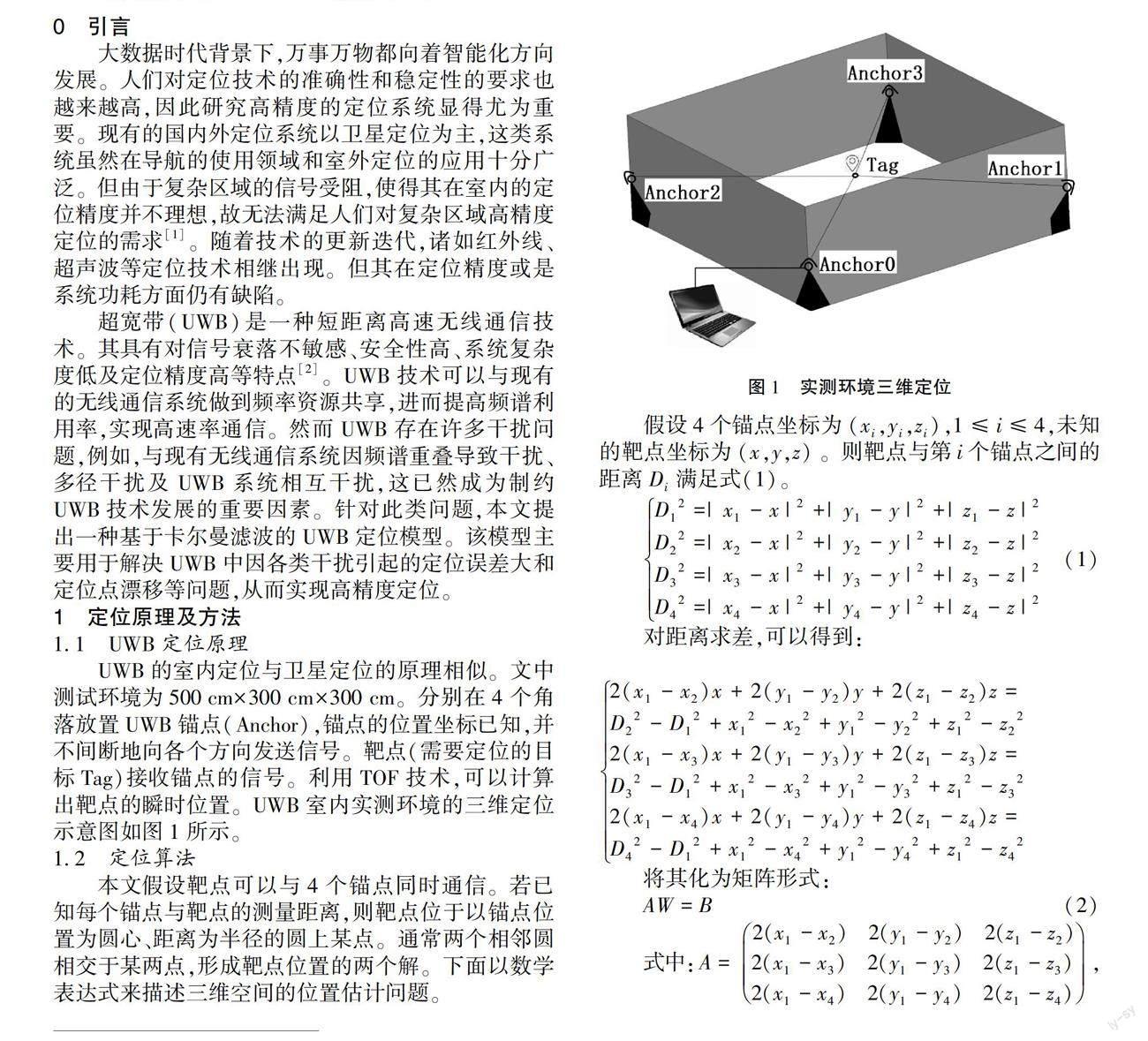
UWB的室内定位与卫星定位的原理相似。文中测试环境为500 cmX300 cmX300 cm。分别在4个角落放置UWB锚点（Anchor），锚点的位置坐标已知，并不间断地向各个方向发送信号。靶点（需要定位的目标Tag）接收锚点的信号。利用TOF技术，可以计算出靶点的瞬时位置。UWB室内实测环境的三维定位示意图如图1所示。

1.2 定位算法

本文假设靶点可以与4个锚点同时通信。若已知每个锚点与靶点的测量距离，则靶点位于以锚点位置为圆心、距离为半径的网上某点。通常两个相邻圆相交于某两点，形成靶点位置的两个解。下面以数学表达式来描述三维空间的位置估计问题。

综上，根据最小二乘法可以计算出靶点的三维坐标。

W= （ArA） -'ArB

（3）

1.3 基于线性卡尔曼滤波的定位模型

卡尔曼滤波目前已经广泛地应用于制导与控制、导航和通信等多个领域。其可理解为一种递归算法，即根据当前的测量值、前一时刻的预测值和误差，递归当前时刻，再预测后一时刻的状态估计法[3]。由于室内定位环境复杂，文中采用卡尔曼滤波法对解算后的位置坐标进行平滑处理，尽可能地消除因外界脉冲干扰带来的测量误差。

（1）计算出靶点的三维坐标。

已知测试环境中锚点位置（单位：cm）为Al（O．0.120）、A2 （500.0. 160）、A3（0，300. 160）， A4（ 500.300，120）。假设锚点和靶点之间的信号传播在视距范围内。靶点采集到10组相关数据，并提供了锚点与靶点的距离值（ cm）。其中前5组数据无信号干扰，后5组数据有信号干扰。此处选取一组数据（330，313，290，279），根据定位算法得到相应的靶点坐标见式（4）。

2 结果与讨论

本节旨在使用卡尔曼滤波对UWB定位后的坐标数据进行平滑处理，以减小数据误差，从而提高定位精度。下面进行模拟环境下的静态定位测试。

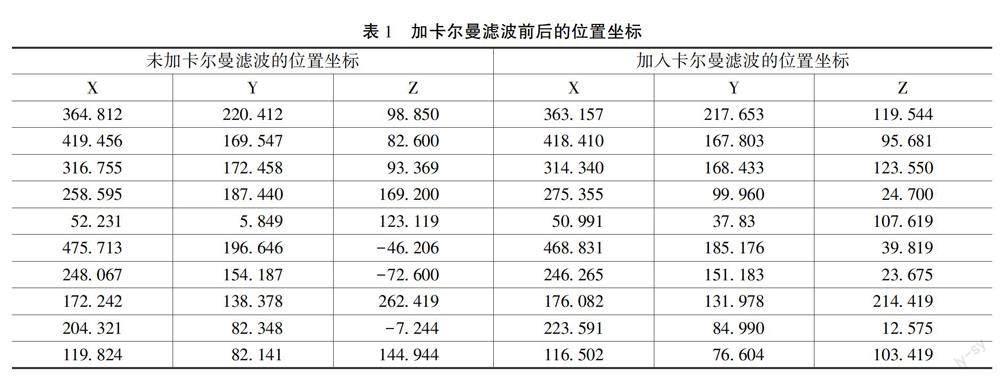
首先，基于靶点采集到的数据，通过定位算法得到靶点坐标。然后，利用Matlab中的Simulink模块搭建Kalman位置模型。最终得到10组优化前后的靶点坐标如表1所示。

表1表明了加入卡尔曼滤波后的位置坐标更加合适，提高了定位精度。并且卡尔曼滤波算法相较于其他算法而言，执行速度更快。为了更直观地观察加入卡尔曼滤波的效果，如图2所示给出了滤波前后10组数据的误差值。

从图2可以清晰地看出加入卡尔曼滤波进行平滑处理后的数据误差明显减小，且较为平稳。相比于未加入滤波前的位置数据而言，滤波后的数据更具有参考性。

3 结语

本文提出了一种基于卡尔曼滤波的UWB室内精确定位技术，旨在解决UWB定位技术的测量精度不够高的问题。具体地依据UWB定位原理以及靶点采集到的数据得到靶点坐标，结合卡尔曼滤波法对坐标进行了平滑处理。并且通过分析模拟实验的静态定位误差，证实了本文的定位模型一定程度地提高了定位精度。该方法能够更加准确、可靠地定位。但室内环境较为复杂，该定位技术必要时需进行趋势分析和补偿，进一步提高该模型应用的鲁棒性。

参考文献

[1]刘永昌，龚元明．基于卡尔曼滤波的超宽带定位技术应用[J]．软件工程，2021（7）：24-27.

[2]陈炜翰，李世银．基于超宽带和微惯导组合的室内精确定位[J]．电子元器件与信息技术，2020（1）：24-26.

[3]杨玉林．基于卡尔曼滤波和粒子滤波的目标跟踪性能对比[J]．佳木斯大学学报（自然科学版），2021（3）：72-75，78．

[4] CHEN C， WU X， BO Y， et al.SARSA in extendedKalman Filter for complex urban

environmentspositioning[J].International Journal of Systems Science，2021（18）：1-16．

[5lSAINZ J J，REVESTIDO H E， LLATA J R，et al.LQG control for dynamic positioning of floating caissonsbased on the Kalman fiher[J].Sensors. 2021（ 19）： 1065.

（編辑傅金睿）