基于Dijkstra算法的社区公共体育设施空间可达性策略研究
李兆进 孙彦姝 秦宝兰 赵艳 郭雅如 杨玉颖

摘 要:随着健康中国战略的有序推进,如何满足居民不断增长的健身需求,加强公共体育设施建设,合理规划健身场地布局,成为社会关切问题。本研究以日照市东港区大学城公共体育设施为研究对象,通过问卷调查、实地走访与数据分析等方法对社区公共体育设施的数量及分布进行分析。以日照大学城为例,利用Dijkstra算法建立最短路径模型以选择公共体育设施最佳分布位置。同时利用空间可达性理论对选址进行分析与评价,最终提出大学城公共体育设施空间布局优化策略。
关键词:公共体育设施;空间布局;Dijkstra算法;可达性
中图分类号:G812.7文献标识码:A文章编号:1009-9840(2023)02-0001-07
Spatial Accessibility Strategy of Community Public Sports Facilities Based on Dijkstra Algorithm: A Case Study of Rizhao University Town
LI Zhaojin1, SUN Yanshu2, QIN Baolan2, ZHAO Yan2, GUO Yaru2, YANG Yuying2
(1. School of P.E., Qufu Normal University, Qufu 273165, Shandong, China; 2. School of Management, Qufu Normal University, Rizhao 276821, Shandong, China)
[WT5HZ]Abstract:With the proposal of healthy China strategy, how to meet the increasing demand of residents for fitness, strengthen the construction of public sports facilities and rationally plan the layout of fitness venues have become social concerns. This paper takes the public sports facilities in the university town of Donggang District of Rizhao city as subject, and investigates the number and distribution of community public sports facilities through questionnaire survey, field visits and data analysis. Taking Rizhao University Town as an example, the shortest path model is established with the Dijkstra algorithm to select the public sports facilities in the best distribution location. Meanwhile, the spatial accessibility theory is used to analyze and evaluate the site selection and finally put forward the spatial layout optimization strategy of public sports facilities in university towns.
Key words:public sports facility; spatial distribution; Dijkstra algorithm; accessibility
“没有人民健康,就没有全面小康”。2021年7月18日,国务院印发《全民健身计划(2021-2025年)》明确指出,社区体育是全民健身的坚实基础,应充分挖掘存量建设用地潜力,规划建设贴近社区、方便可达的场地设施。2022年3月23日,中共中央办公厅、国务院办公厅印发了《关于构建更高水平的全民健身公共服务体系的意见》,指出构建更高水平的全民健身公共服务体系,是加快體育强国建设的重要基石,是顺应人民对高品质生活期待的内在要求,是推动全体人民共同富裕取得更为明显的实质性进展的重要内容。应以公益性和基础性为导向,扩大满足群众体育健身和运动休闲需求的场地设施,注重因地制宜扩大全民健身公共服务体系供给。但在健康中国战略和全民健身工作不断推进的过程中,存在社区体育场地数量、体育设施配置和体育空间结构规划居民需求不匹配的现象[1],极大地影响全民健身战略的实施和深入开展。因此,建设便利可达,群众可及,服务健全的适老化、示儿化、适龄化的城市社区全民健身空间将成为人民所急、社会关切、国家所需的重要任务之一,是不断完善公共体育服务、优化体育设施布局,构建更高水平的全面健身公共服务供给的关键[2]。
社区体育是居民在特定区域内自行组织和参加的一项体育锻炼活动。本研究从社区公共体育设施建设如何满足群众健康生活需求出发,以日照市大学城为例,运用文献资料法和逻辑分析法,对城市社区公共体育供给失效的主要影响因素进行分析,借助Dijkstra算法与可达性分析对日照大学城公共体育设施场地的空间分布进行可达性路径统筹,并提出优化策略与建议,以完善城市社区体育服务体系,助力全民健身的实现。
1 公共体育设施布局调研分析
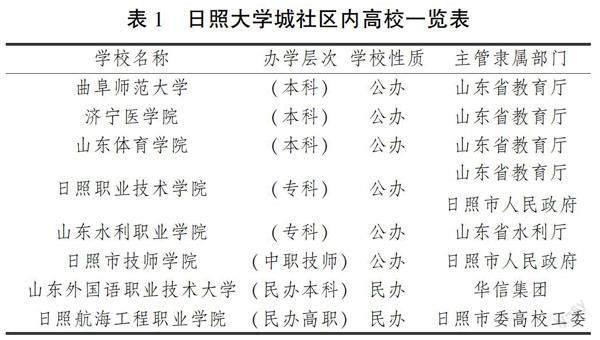
研究以日照市大学城社区为例进行公共体育设施布局和可达性调研分析。日照大学科技园成立于2001年11月,现有面积25平方公里,共有8所高校(见表1),约6万在校学生入驻,是集学习生活和科研产业于一体的综合性大型社区。
1.1 布局概况
日照大学城社区体育活动场所主要集中在社区空地,而距离社区公园较近的大学生和社区民众则选择公园步道为健身场地,参加盈利性场所健身的居民占少数。学校体育场地因承担学生的教学与课余活动需要,虽对大学生开放程度较高,但对居民开放程度并不理想[3]。目前,大学城区内体育场地设施缺乏、学校体育活动场所开放度低,不能满足社区居民体育需求,成为影响日照市大学城社区体育发展的主要因素。在社区体育场地设施尚未兴建的境况下,以大学城区内存量体育场地设施为依托,整合优化区内空间体育健身资源布局,就成为解决大学生与社区居民体育健身高需求度和低供给度矛盾的有效策略[4]。
1.2 公共体育设施布局和可达性存在的问题
1.2.1 分布不均衡,供需矛盾突出
尽管当前日照市东港城区兴建开发了部分体育场地设施,但大学城民众日益增长的体育需求与体育设施数量短缺的矛盾依旧突出。分析原因,一方面是日照市体育场地设施资源的存量较低,无法在短暂几年内大幅增多;另一方面,近年来我国社会经济发展水平的不断提高带来了城乡居民体育消费观念的显著变化,尤其在大学城区选择体育活动及经常锻炼的人群数量大大增加,这使得群众体育场馆资源出现紧张局面。最后,相较于村镇而言,大型社区内存在较为集中的大型体育设施。但外围区的公共体育设施建设相对滞后,呈现出“内重外轻”的布局现象。
1.2.2 利用率不高,缺乏科学管理
根据对物管部门的走访和现场实地调查,大多数社区的体育设施、体育场馆多未得到较为科学的使用,且未形成科学的管理规定体系,更缺乏体育设施使用指导说明。在社区体育设施维护方面严重缺乏,例如,不少村镇多数公共体育设施器材已经损坏,大部分器材都已经十分陈旧,没有相应专业人员管理维护。而且没有配备社会体育指导员进行器材使用和健身指导,导致安全事故隐患加大和设施器材损坏程度加速。相比于社区,这种情况在村镇尤为突出。另外,部分园区把室外健身设施放在室内和小区的偏僻角落,导致场馆利用率低[5]。
1.2.3 布局不科学,空间可达性差
社区公共体育设施在空间视域下分布地点较为古板,在用地选择与布局上,缺乏与城市总体布局的协调,造成可达性差,使用不方便,甚至与城市其他功能冲突。周边新建、扩建、改建的居民商区,未能及时配套群众健身相关设施,或未与主体工程同步设计、同步施工、同步投入使用。体育设施资源空间分布不科学,未能科学设计15 min健身圈。
1.2.4 配套不健全,服务功能不足
体育健身设施更新不及时,配套设备不健全、辅助设施不充足等问题突出,社区内体育健身公共服务不到位,体育活动开展不通畅,难以适应现代化大学城社区的健身需求。由于空间布局的不科学和配套设施的不健全造成體育健身引发的安全、噪声、垃圾等问题突出。
2 公共体育设施布局可达性分析
2.1 网络分析法
2.1.1 方法简述
最短路径问题是图论研究中的一个经典问题,在实际应用中,它不仅指一般意义上的距离最短,诸如时间、费用等均可引申为最短路径,即最短时间问题、最低费用问题。网络优化路径包括最短路径分析、资源配置、时间性问题等,而网络模型,是指将现实中的地理网络实体,抽象化为图论理论中的网络图,并通过图论中的网络分析来实现地理网络的最优化问题[6]。
Dijkstra 算法是一种被广泛应用的最优路径搜索算法,作为最著名的路径搜索算法之一,它被广泛应用于各类图的最短路径求解上。该算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径,其主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止[7]。
2.1.2 基本思想
在Dijkstra问题中,一般设G=(V,E)是一个带权无向图,把图中顶点集合分成两组,第一组为已求出最短路径的顶点集合,用S表示,初始时S中只有一个起源点v,以后每求得一条最短路径,就将标记点加入到集合S中,直到全部顶点都加入到S中,算法结束;第二组为其余未确定最短路径的顶点集合U,按最短路径长度的递增次序依次把第二组的顶点加入S中。加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
现假设每个点都有一对标号(dj,pj),其中dj是从起源点v到点j的最短路径的长度(从顶点到其本身的最短路径长度等于零);pj则是从v到j的最短路径中j点的前一点[8]。求解从起源点v到点j的最短路径算法的基本过程如下:
(1)初始化。起源点标号为:ds=0,ps为空;其他所有点标号为:di=∞,pi=?;标记起源点v,记作k=v,其他所有点在集合U中。
(2)检验集合S中所有已标记的点k到集合U中所有未标记的点j的距离,并设置为:
dj=min[dj,dk+lkj]
式中,lkj是从点k到j的直接连接距离。
(3)选取下一个点。从集合U中,选取dj中最小的一个点i。
di=min[dj,集合U中的点j]
(4)找到点i的前一点。从集合S中找到直接连接到点i的点j*,作为前一点,并设置为:i=j*
(5)标记点i。如果所有点已标记,则算法完全退出,否则记k=i,转第⑵步继续计算。
因此,Dijkstra算法的一般运算流程如图2所示。
2.1.3 数据分析
以日照市东港区秦楼街道大学城为例,根据前期的走访发现三处较为适合体育健身的场所:其一为大学城中心电子商务科技园附近的人民防空公园,其地理位置优越但公园中缺少体育健身器材的设置;其二为东港区学苑路时空广场,占地宽阔但体育健身器材稀少;其三为东营路与烟台路附近的全民健身体育公园,其设施设备专业完善但地理位置于大学生来说相对偏远。因此,为满足大学生以及附近居民对运动健身的需求,本研究将对上述地点到达各宿舍园区的最短路径进行描述分析。
现以各园区各校学生前往人民防空公园为例,以大学城公交专线中时间最短的路线为参照,跟据走访调查显示,人民防空公园与各大学校园区的距离分布如表3。
经过数据统计与整理,将现实中的地理网络实体,抽象化为图论理论中的网络图,现根据各区域的空间分布进行模型简化,利用Dijkstra算法求最短路径,将大学城基本分布情况简化为带权无向图。以38路公交线路为基础,1号表示人民防空公园,2~8号分别表示山水职院、山东体院、济医学院、曲阜师大、日职学院、山外职大以及日航职院。标号之间的数字表示各地之间的距离权重,将路径简化为线段,具体如图4所示。
由此可以得出的结论为:
(1)邻接矩阵是表示顶点之间相邻关系的矩阵,对于无向图而言,由于顶点之间没有严格规定的起止方向,因此边(1,2)与边(2,1)表示同一条边;
(2)无向图所对应的邻接矩阵一定是对称矩阵,并且主对角线一定为0;
表中将距离转化为权重,数字Dij表示第i个节点到第j个节点的权重。
2.2 最短路径模型
2.2.1 计算过程
现以1号电子科技园到8号日照航海工程学院为例,计算1号到8号的最短路径。计算顺序如下(lnf表示无穷大):
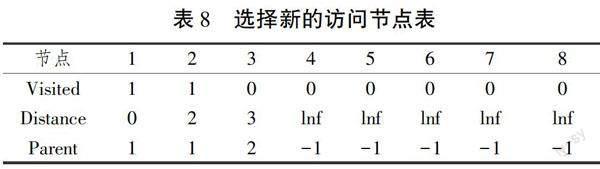
(1)初始化。①所有的节点都是未访问节点(访问状态:0代表False,1代表True);②所有的距离都是lnf无穷大;③将已标记节点的前一点j*称为父节点,现所有父节点为-1,表示不存在,如表5所示。
(2)假定起点为1,对起源点进行状态更新。①将节点1对应的访问状态变为1;②节点1对应的访问距离为0;③节点1的父亲节点用自身表示,如表6所示。
(3)表2中,改变访问状态的节点为1号节点(A),应更新与1号节点相邻的节点信息B,B∈U。若lAB+节点A的访问距离<节点B的访问距离,则将列表中B的距离更新为最短距离,其父亲节点为A。在本研究中,由于与节点1相邻的节点为2、3,则:1号与2号的距离为2,2+0<lnf,所以更新节点2对应的表格信息;1号与3号的距离为4,4+0<lnf,所以更新节点3对应的表格信息。如表7所示。
(4)在所有未访问节点中寻找最短距离的点来作为新的访问节点。显然,在上述表格中2号对应的距离最小,所以我们将2号视为已访问节点,如表8所示。
(5)以上为第一轮节点的选择。按照上述规律,继续标记访问节点。如表9、表10所示。
(6)将已标记的节点按照顺序连接,形成最短路径。
由上图5可知,从人民防空公园到达航海学院的最短路径为1-2-3-5-6-8。同理,可根据上述步骤计算出各校区到达航海学院的最短路径,以及各校区到达学苑路时空广场与全民健身体育公园的最短路径。
2.2.2 计算结果
以人民防空公园为例,针对体育设施资源优化布局的“最短路”系统,建立假设,并构建以A为起点单源最短路径的Dijkstra数学模型。本问题利用MATLAB软件来进行求解计算,所绘制的最短路径如6图所示。
从图6可以清晰看到由1号到达8号的最佳路径为1-2-3-5-6-8,利用Dijkstra算法可求出1号到达各个地点的最短距离。同理,分别建立时空广场运动中心与全民健身体育公园到达各地点的最短路系统,通过MATLAB绘制最短路径结果图,比较各学校到达三处的平均最短距离,选择最佳建设地点。
2.3 可达性分析与评价
2.3.1 空间可达性数学模型
考虑到影响最短路径的因素不仅受地理或空间距离的影响,同时受到经济、行为、观念的影响[9],为进一步比较分析三处地点在大学城分布的合理性,利用空间可达性数学模型进行深入研究。
本研究采用Allen提出的最小阻抗的可达性分析方法[10],该法利用中心点至所有体育设施目的地的平均最小阻抗作为中心点的可达性评价指标。基于最小阻抗的可達性分析方法属于网络分析法,公式如下:
如上公式,Mi表示设施布局网络上的各节点i的可达程度;M为整个网络的可达性;eij表示节点i、j间的最小阻抗,可以表示为距离、时间或费用等。
公式(1)表明,节点i的可达性,为该节点到网络上其他所有节点的最小阻抗的平均值,最小阻抗可以为最短距离、最短时间、最少费用等。公式(2)表明,整个网络的可达性为各个节点可达性的平均值。本研究选取的最小阻抗为到达运动中心的最短时间。
2.3.2 研究数据的获取与整理
本研究通过实地调研日照市大学城基本道路数据可得到出行地点到达目的地点之间的最短距离,通过分析大学城出行地至该体育设施之间的最短可达距离与不同出行方式,得出其“距离—时间”分布表,同时在所得“距离—时间”分布表中对最短可达时间进行汇总。
将日照市东港区大学城基本地区情况简化分析,R表示人民防空公园,A-G分别代表山水职院、山东体院、济医学院、曲阜师大、日职学院、山外职大以及日航职院。
由于大学城内学生在选取出行方式时,其可达时间随出行方式变化而改变,因此在本研究中,首先选取步行、骑行、驾车、乘公交四种交通方式。以日照职院出行方式为例,在计算最短交通时间时,其交通方式有4种。通过实地调研可知,域内各种交通方式的对应时间为:步行需28 min、骑行需11 min、乘公交需17 min、驾车需7 min。最终结果择驾车时间为最短可达时间,并由此进行下一步计算。由此类推,其他出发地到达目的地的最短交通时间皆由此法计算,具体表11所示。
经过数据统计,利用公式(1)(2),将处理数据依次导入公式。已知n=7,计算后得到R地的可达性为7.7。
利用相同的计算过程,重复选取目的地点并简化为序号,S表示时空广场运动中心,Q为全民健身体育公园,在出发地固定相同的情况下,再通过上述方法来分别计算S、Q两处目的地对应的基于最小出行时间为阻抗的可达性,求得结果分别为7.87和8.3。
从结果可知,R地所对应的可达性数值低于S、Q两地的可达性数值,可以由此知人民防空公园具有较高的布局优化程度,可达效果更优。
2.3.3 可达性结论分析
本研究中用最小出行时间作为阻抗,将大学城内选取的A-G地作为出发点,将在R、S、Q三地作为目的地,计算出发点到目的地的平均最短交通时间,以此作为可达性的评价指标,衡量各居民区到体育设施场地入口的交通便捷程度。
结合上述原理,可以对日照市大学城内所选定的体育设施可达性现状进行总结。
(1)各出发地抵达人民防空公园的最小出行时间为阻抗的可达性值为最低,其体育设施服务能力在东港区大学城中最佳;与之相比,东港区学苑路时空广场与全面健身公园的最短可达时间较高,其体育设施服务能力较差。
(2)根据东港区大学城内公共体育设施的可达性分析可知,在计算出发地与目的地之间的平均最短出行时间时,最短出行时间涉及的交通方式多为驾车,考虑到大学城内民众多为学生身份,且其经济能力和个人偏好并不一致,这对模型的适配性提出要求。对整体的规划布局来看,公共体育设施的服务展现高度效能,在影响民众与体育设施之间多样可达性中具有重要的作用特征。
(3)同样,考虑到大学城内道路交通情况与人流分布情况,驾车的出行方式虽然时间短,但未必可达性强。驾车出行容易受到交通拥堵、人流众多的影响,相较于骑行而言,缺乏便捷性、灵活性。
3 结论与建议
3.1 实现公共体育设施运行与管理科学化
综合调研发现,日照市东港区部分社区体育健身设施已经损坏,大部分器材都已较为陈旧,并且缺乏相应专业人员的管理。居民在锻炼时也没有配备专业的体育指导员进行指导,导致安全事故隐患加大和设施器材损坏程度加强。因此,实现公共体育设施运行与管理科学化是保障公共体育设施高效利用的关键[11]。
(1)将公共体育服务空间布局纳入城市公共服务的总体规划,优化公共体育设施布局,通过建立相关政策,对优化城市公共体育设施布局进行科学管理。
(2)对体育健身器材实行责任制管理,落实社区的属地管理原则,社区可以设立专职或兼职社会体育指导员,从属地管辖和人员职责上加大对体育设施的管理和维护,对一些已经达到室外健身器材使用寿命需要淘汰的器材及时进行清理、淘汰,保证器材使用的安全。
(3)将公共体育设施管理纳入物业管理范围,明确设施维修管理职责,由体育部门督查,管理内容应包含行政管理和器材的售后服务。同时,进一步促进室外健身器材的提档升级,强化器材的质量,并提高智能化水平,让室外体育健身器材更好地造福群众。
3.2 提升公共体育设施空间均衡优化布局
东港区公共体育设施资源存在着分布不均衡问题,尤其是郊区乡镇体育设施相对不足,且各大学园区体育器材有限,缺乏必要的大型公共体育场馆。因此,灵活调整效益不佳的现有用地、现成建筑物的功能,改造成适宜的健身场所是一项必要任务。东港区作为典型的大学生集聚城市,公共体育设施需求量较大,且地貌类型多样,城市形态的扩展受到了人口密度、地形的制约,在此条件下,东港区应统筹考虑社区公共体育设施布局的功能,判断各区域面积与公共体育设施数量是否符合规划标准要求,考虑公交车路线、人流量等因素并利上文求出的模型选择合适的地址并进行检验地址的合理性,在缺乏公共体育设施的区域建设配套有更衣室、小型餐饮、器材租售等系列的公共体育运场地[12]。
3.3 加大公共体育设施智慧化服务建设投入
物理空间是有限的,大学城随着公共体育设施的增加,要充分利用所有公共体育场地,就需要引用信息化设备强化服务功能,增强发展活力,通过新媒体、信息化、VR等拓展体育衍生空间,吸纳更广的场外空间,更好推动各类全民健身活动的开展。
3.4 促進公共体育设施与其他公共场所融合
针对部分社区增加公共体育设施场地面积较为困难的情况,可充分考虑社区公共体育设施场地与其他体育场所的结合,尽量满足群众的体育运动需求。专业体育场馆可在结束专业体育训练、比赛后,尽可能地、有计划地与社区合作,向群众实行有偿开放或承办大型文艺活动,通过适当延长开放时间以满足不同年龄层次和不同工作时间安排的群众对于体育锻炼的需要[13]。
4 研究展望
在“全民健身”的大背景下,本研究对影响公共体育设施规划布局的各种因素进行了梳理,分析日照市东港区大学城公共体育设施布局现状,从城市规划管理和运筹学视角提出基于普通民众体验的公共体育设施规划理论方案以及基于分级标准体系的布局优化模型进行比较分析,归纳总结了日照市公共体育设施布局规划的策略和方法,为后续研究提供思路。
展望我国城市公共体育设施布局规划的未来发展,应当在借鉴先进城市经验的基础上,充分尊重现有城市的基本情况和地域特色,以满足不同城市居民的体育设施需求,打造具有城市特色的公共体育设施优化布局方案。而本研究利用Dijkstra算法建立最短路径模型以选择公共体育设施最佳分布位置,同时利用空间可达性理论对选址进行分析与评价,最终提出东港区公共体育设施空间布局优化策略的方法具有较大的包容性,能够对多种因素进行综合考量,充分尊重了各城市的特点,可为我国其他城市公共体育设施的空间布局提供借鉴借鉴。
参考文献:
[1]陈兵.社区体育休闲生活方式的立足点—社区体育“以人为本”的讨论[J].邢台学院学报,2018,3(4):176-178.
[2]曹华,樊炳有.局限、架构与实施:综合治理适用于体育公共服务供给的逻辑阐释[J].山东体育学院学报,2021,37(4):19-25.
[3]顾兴全.城市基本公共体育服务设施供给标准化研究[J].北京体育大学学报,2018,41(3):33-39.
[4]陈畅,刘爱华,周威.快速城镇化中城市边缘区人口空间重构初探—以天津市为例[J].城市规划,2016,40(10):17-22.
[5]王浩.浅谈我国群众体育场地设施突出问题的原因与对策[J].体育时空,2017(7).
[6]蒋腾飞.网络最短路径问题与应用研究[D].南京:南京邮电大学,2013.
[7]乐阳,龚健雅.Dijkstra最短路径算法的一种高效率实现[J].武汉测绘科技大学学报,1999(3):209-212.
[8]王小会,薛延刚,李晓青.基于Dijkstra算法过必经点的最短路径设计[J].陕西理工大学学报(自然科学版),2020,36(3):68-73.
[9]张峰筠,肖毅,吴殷.城市社区公共体育设施场地的空间布局—以上海市杨浦区为例[J].上海体育学院学报,2014,38(1):80-83.
[10]郦晓桐,杨鑫.基于网络分析法的北京市石景山区公园绿地可达性研究[J].华中建筑,2016,34(10):83-86.
[11]赵蕊.社区体育枢纽式管理模式的研究—以上海市社区体育协会为例[J].体育成人教育学,2016,32(3):65-68.
[12]毕红星.我国城市公共体育设施规划布局研究[J].成都体育学院学报,2012,38(4):34-38.
[13]巴艳芳.城市体育设施空间布局与体育产业发展对策研究[D].武汉:华中师范大学,2006.
收稿日期:2022-04-14
基金项目:国家社会科学基金一般项目(编号:21BTY115);山东省大学生创新项目(编号:S202110446175)。
作者简介:李兆进(1977- ),男,博士研究生,副教授,硕士生导师,研究方向为体育产业与体育管理、传统文化。

