基于强化学习的车辆服务迁移方法

周 率， 韩 韧

（上海理工大学光电信息与计算机工程学院， 上海 200093）

0 引 言

随着《车联网（智能网联汽车）产业发展行动计划》通知的下发，中国车联网发展的战略目标已基本确定，“长三角三省一市统筹智能网联汽车产业发展规划”的签署进一步加快了中国车联网的发展。 5G 网络基础设施的不断完善以及国内外车联应用的涌现，使得车辆对计算资源和服务延迟的要求日益增加，现有车辆配备的计算资源已无法满足车联应用的需求，这种日益迫切的要求需要将车联应用服务迁移到具有更高计算能力的云端服务器上，但是传统的云计算不能满足车联网下的低延迟要求，因此需要考虑一种称为车载边缘计算（Vehicular Edge Computing，VEC）的计算范式。

在VEC 中，车辆将服务迁移到靠近车辆的路侧单元（Road Side Unit，RSU）上，可以享受RSU 带来的低延迟、高带宽和充足的计算资源［1］。 然而，盲目的迁移有时会影响服务性能，如：对于一个固定的车辆，将服务迁移到最近的RSU 在短期内可以带来良好的服务性能，但是考虑到车辆的移动性，该种策略可能会导致频繁迁移，进一步导致服务频繁中断，因此一个最佳的服务迁移策略应该考虑车辆的移动性。 服务迁移也伴随着各种成本，包括计算成本、迁移成本和能源消耗，以全面评估迁移的效果。 考虑到车辆的移动性，专注于短期的性能提升可能会导致频繁迁移因而带来巨大的成本，需要考虑迁移带来的长期累积回报，以权衡整体性能的提高。 即当车辆远离RSU 时，如果服务性能仍然处于可接受的水平，一个最佳的迁移策略应该权衡服务迁移带来的收益与开销。

为了提高服务迁移的性能表现，减少服务的延迟与开销，文献［2］研究了最小化移动设备和边缘服务器的总能量消耗，通过启发式算法产生了一个接近最优的解决方案；文献［3］提出在卸载比例和子载波分配时，必须考虑各种系统限制，包括延迟和子载波资源限制，以减少移动设备的能耗，并从混合整数规划（Mixed Integer Programming，MIP）问题中生成多对一匹配和线性编程的子问题，以解决子载波分配问题；文献［4］研究了下行链路资源分配、卸载决策和计算资源分配的联合优化，考虑了包括数据传输和任务计算的总成本，并建模为混合整数线性规划（MILP）问题；文献［5］提出了李雅普诺夫优化的卸载决策，可以减少平均响应时间，同时降低移动设备的能耗；文献［6］评估了计算卸载的财务成本，并建模为决策和资源联合优化的MILP 问题；文献［7］以合作博弈理论为基础，通过终端设备和边缘云的协同合作来优化系统的性能，并提出了一种基于交易的计算卸载技术；文献［8］提出了Follow－Me Chain 算法来解决服务功能链的问题；文献［9］研究了任务卸载，考虑了能耗和服务延迟的约束，并使用了二元卸载决策；文献［10］提出了一个基于强化学习的离线无线接入网络分片解决方案和一个低复杂度的启发式算法，以满足不同分片的通信资源需求，使得资源利用率最大化；文献［10］将迁移问题建模为一维马尔科夫决策过程（Markov Decision Process，MDP），并考虑了服务器和设备之间的欧氏距离；文献［12］考虑了二维MDP 模型并提出了基于深度强化学习的迁移方案，使得时延与能耗最小。

尽管现有的工作在服务迁移策略方面取得了很大的进展，但仍需要进一步探索，包括迁移过程中成本的建模以及车辆的移动性。 本文将车辆的服务迁移过程建模为MDP，同时考虑了包括计算成本、迁移成本和能耗的成本，此外，本文还使用行驶速度代表示车辆的运动状态，并提出了一种基于强化学习的迁移算法，该算法可以有效地解决传统MDP 中维度过高的问题，并利用Actor－Critic 网络和熵来确保收敛性和可探索性。 最后，本文基于真实数据集进行实验并对算法进行评估。

1 系统模型建立

车辆行驶随机分布在城市区域的道路中，道路配备了若干通信范围相等的RSU，并且每个RSU 都具有相同的计算能力。 用E＝｛e1，e2，…，ei｝ 表示所有RSU 的集合，用U＝｛u1，u2，…，uj｝表示所有车辆的合集，每个车辆u∈U都有一个计算任务且可以选择在本地计算或者通过无线网络迁移到RSU 上。车辆移动时可以连接到任意一个路侧单元e∈E。为了保证车辆采取迁移决策时的满意程度，本文用迁移成本，计算成本，能源消耗等相关指标来衡量服务迁移过程中产生的开支。

1.1 通信模型

本文假定车辆通过V2X 的蜂窝网络和毫米波与RSU 进行通讯。

1.1.1 5G 蜂窝网络

根据香农公式，在假定被高斯白噪声干扰的信道中，理论的最大信息传输速率为公式（1）：

其中，B是信道带宽；S是信道内所传输信号的平均功率；N是信道内部的高斯噪声功率。

因此，车辆u和路侧单元e之间的数据传输率可以表示为式（2）：

其中，Bc是信道带宽；Hu，e是车辆u的车载通信设备与其对应的路侧单元e的传输功率；du，e表示车辆u与路侧单元e的距离；h表示瑞利衰落因子；Nc是高斯噪声功率。

1.1.2 毫米波模式

NR－V2X 采用毫米波模式，本文假定每辆车辆都配备有定向天线阵列，并且采用了定向波束形成来增强毫米波信号的传播。 为了最大化提高毫米波天线的指向性增益，本文假定对发射器和接收器进行光束准直，因此可以将定向天线模式近似为理想的水平面上的扇形模型［13］，天线增益可以建模为式（3）：

其中，η为当前天线的角度与当天线增益达到峰值时的角度之差，即天线转向方向的可容忍对准误差；η′是射束宽度；gm和gs分别是主瓣和旁瓣天线的定向增益。

在上述条件下，本文将毫米波信道带宽表示为式（4）：

其中，Bm是毫米波信号带宽。

车辆天线与基站天线的信噪比为式（5）［14］：

其中，pu是车辆u配备的毫米波收发器的传输功率；Nm是噪声功率谱密度；du，e表示车辆u和路侧单元e间的曼哈顿距离；ρ～N0，σ2() 是以分贝为单位的阴影衰落模型；而σ为标准偏差。

1.1.3 通信模型

车辆与RSU 的数据传输速率可以表示为式（6）：

其中，λc，λm分别为代表是否使用5G 蜂窝网络或NR 模式进行通讯的二元变量。

当λc＝1 时，假设车辆u使用5G 蜂窝网络作为通讯方式，λm＝0；反之当λc＝0 时，λm＝1 认为车辆u使用NR 模式作为通讯方式。

1.2 迁移成本模型

本文使用了平台服务（PaaS） 范式，并采用Docker 技术，该技术具有增强应用程序可移植性的机制，可以让应用程序无环境差异地部署在各个地方，因此本文将服务迁移成本建模为Docker 服务镜像迁移成本。 假定每个车辆都包含计算任务，且任务定义为一个二元组：Tu＝ {pu，Su}，其中pu是完成任务Tu所需的计算资源，Su代表车辆u执行的服务镜像大小。

本文采用了部分迁移而非二元迁移，并假定车辆u卸载到远程路侧单元e的服务比例为， 表示为式（7）：

其中，表示车辆u卸在本地执行的服务比例。

据服务镜像大小，可以得出在路侧单元e执行的服务的镜像大小，式（8）：

因此迁移成本如式（9）：

其中，λc＝ {0，1}，λm＝ {0，1}，λc＋λm＝1

1.3 计算成本模型

1.3.1 本地车载计算

当车辆u在本地计算时，计算开销的时间取决于其可用资源。 本文假设是车辆u的车载计算资源，则本地计算时间的计算公式（10）：

1.3.2 远程VEC 计算

当本地计算资源紧张或者计算负载过高时，可以将服务卸载到远程路侧单元上进行计算。 在许多包括道路检测和智能制动在内的应用中，因为其镜像的大小远大于从路侧单元传输回来的数据大小，所以本文假定路侧单元返回的计算结果的接收时间忽略不计，则车辆u的远程计算时间表示为公式（11）：

其中，表示路侧单元分配给车辆u的计算资源，pu是完成任务Tu所需的计算资源。

本文假定车辆u卸载到远程路侧单元e的服务比例为， 车辆u卸载本地执行的服务比例为，因此计算成本可以表示为式（12）：

1.4 能耗模型

当本地计算资源紧张或者计算负载过高时，可以将服务卸载到路侧单元上。 在这种情况下，传输能耗可以由公式（13）计算：

其中，ϑe表示车辆u在卸载时的平均传输功率；是服务镜像的大小；Cu，e是车辆u可访问的数据传输速率。

2 基于强化学习的车辆服务迁移

2.1 马尔可夫决策问题

服务迁移策略应该考虑若干成本，在服务迁移过程中对于成本的优化可以采用MDP 进行解决［11］。 MDP 由四元组构成＜A，S，R，P ＞， 其中A代表智能体的所有行动，S是智能体可以感知的环境状态，P是在时隙t状态下的行动将导致下一个时隙t＋1 的状态的概率，R是一个实数，代表奖励或惩罚［15］。

2.1.1 动作空间

本文将时隙t的行动αt∈A定义为

2.1.2 奖励函数

由于强化学习的根本目标在于提升智能体的长期累积回报，因此合理的奖励函数能够提升训练速度与性能表现。 长期累积回报的定义如式（14）：

其中，r(st) 是时隙t中获得的奖励值，γ表示折扣率，用于计算未来奖励值的现值。

本文的奖励函数设计如式（15） ：

其中，ΔGmig(t) 、ΔGcomp(t) 和ΔP(t) 分别表示时隙t迁移成本、计算成本和能耗的下降百分比。

以ΔP(t) 为例，如式（16）定义：

2.2 算法描述

本文采用基于Soft Actor－Critic 的强化学习算法，该算法考虑了预期收益和熵之间的最大化效益，因此最优迁移策略定义为式（17）：

其中，at代表智能体在时隙t采取的行动；st代表智能体在时隙t的状态；γ表示奖励值折扣率；温度参数α决定了熵值的相对重要性；H（π（·∣st））代表熵。

V值表示当前环境状态下开始，未来能获得奖励的期望值，用于表现当前环境状态的好坏程度；Q值表示在选取某个行动后，未来能获得奖励的期望值，该值衡量的是当前选取的行动的好坏程度。V值和Q值之间的关系如图1 所示。

图1 Q 值与V 值关系图Fig. 1 The relationship between Q value and V value

根据贝尔曼方程，V值和Q值可以表示为式（18） 和式（19）：

2.2.1 Critic 网络更新

传统强化学习中，由于维度过高会引发训练困难的问题［16］，因此引入神经网络进行近似，本文提出的算法网络由一个Actor 网络和两个Critic、目标Critic 网络构成。 Critic 网络的损失函数可以表示为式（20）：

其中，θk为Critic 网络参数；D表示重放缓冲区， 可以通过更新；Qθk(st，at) 是时隙t的状态行动价值；y表示目标网络的Q值，可以表示为式（21）：

根据式（20）和式（21），Critic 网络的更新公式为式（22）：

并根据式（23）更新目标Critic 网络：

其中，θk为目标Critic 网络的参数，λ为网络的更新比例。

2.2.2 Actor 网络更新Actor 网络的损失函数通过式（24）计算：

其中，和分别为均值和方差，ε～N（ε） 是正态分布下的噪声参数。

策略参数可以通过式（26）更新：

其中，是从策略中采样得到的，因此可以将其微分。

车辆服务迁移算法见表1。

表1 车辆服务迁移算法Tab. 1 Vehicular service migration algorithm

3 实验

3.1 数据集介绍

为了评估所提出的算法在真实场景中的性能，本文采用微软亚洲研究院在2007 年4 月至2012 年8 月期间在Geolife 项目中收集的GPS 轨迹数据集，该数据集由一连串带有经度、纬度和高度的时间戳的点，包含的轨迹总距离为1 292 951 km，总时间为50 176 h。 同时本文使用阿里巴巴集群数据来模拟真实场景中RSU 的负载，该数据集中包含每台机器的资源使用情况、容器的元信息和事件信息以及每个容器的资源使用情况。

3.2 实验环境

本文的仿真实验硬件平台配置：Intel i5－12500，32 GB DDR4 内存和NVIDIA GTX 3060；软件平台基于Python3.7.9，OpenAI－gym 和Manjaro。 本文将通信范围设定为200 m，实验参数设定见表2。

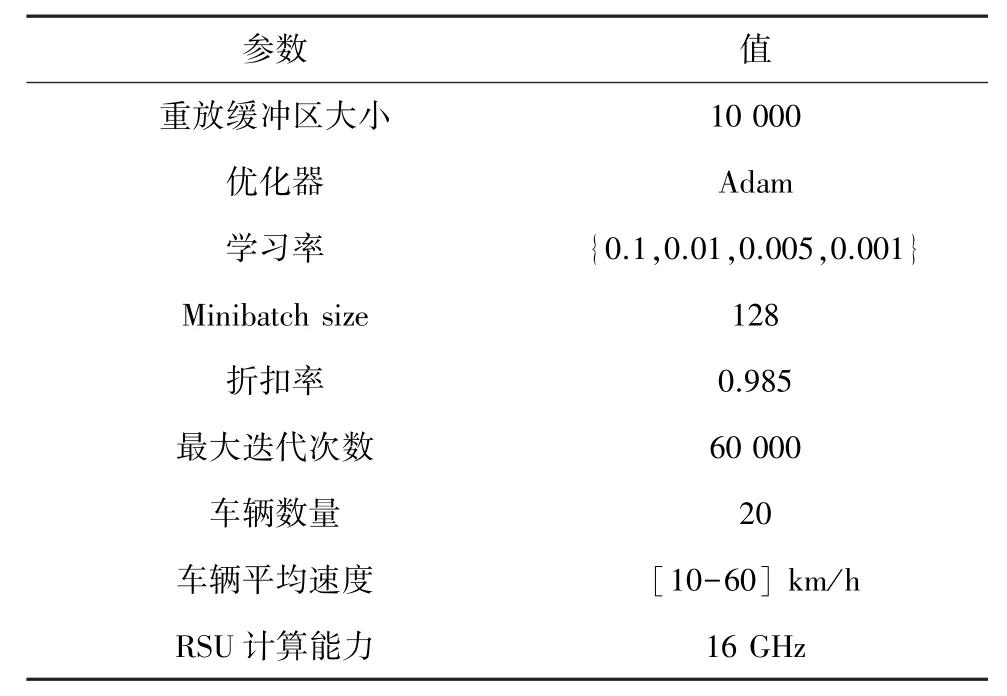
表2 实验参数设置Tab. 2 Experiment parameters setting

3.2.1 算法收敛性

本文首先研究学习率对提出算法的影响，将学习率设置为：0.1、0.01、0.03、0.001，采用在不同迭代次数的平均服务时延作为评价指标，平均服务时延越小，算法的表现也就越好。 学习率对算法收敛性影响的实验结果如图2 所示，当学习率为0.005 时，在经过9 500 次迭代后收敛到最优值并能保持稳定状态；当学习率为0.001 时，在经过15 000 次迭代后收敛；当学习率为0.1、0.01 时，曲线变得极不稳定，而且很难收敛到稳定状态。 因此，研究得出学习率对于算法的稳定程度具有较高影响，这是由于学习率决定了模型权重更新的速度和幅度，对模型的收敛性具有重要影响。 过高的学习率会导致模型在训练过程中无法收敛并出现不稳定的训练行为，使得模型的性能反而变得更差；相反，如果学习率过低，模型的权重更新会变得缓慢。

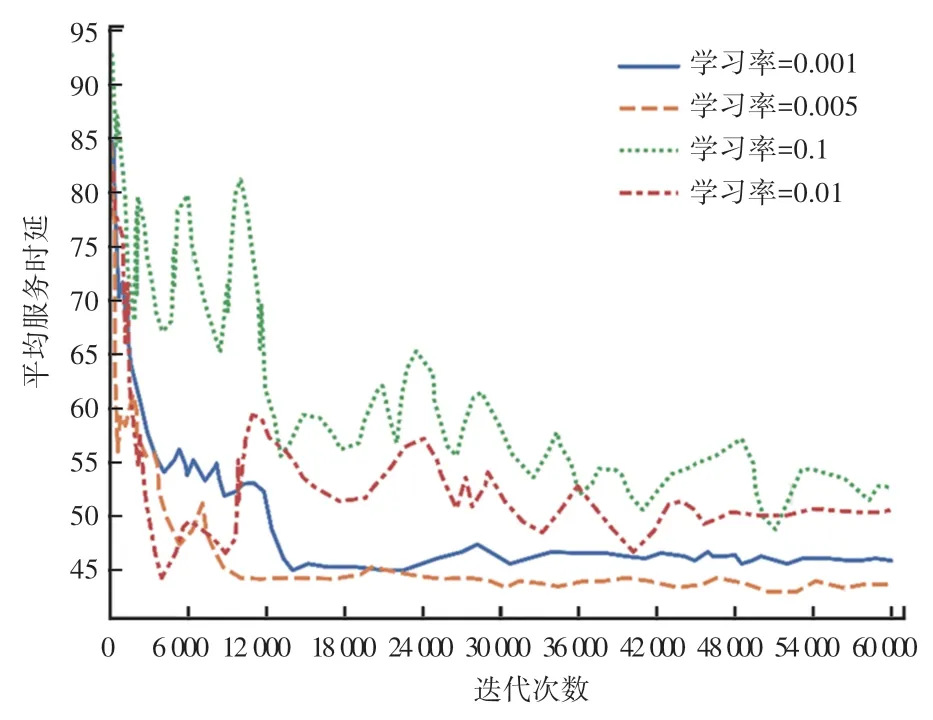
图2 不同学习率对算法收敛性的影响Fig. 2 Effect of different learning rates on convergence

3.2.2 不同算法的服务时延对比

为了进一步验证算法的可靠性，将本文采用的算法与就近迁移（Always Migrate Closely，AMC）、随机迁移（Random）和深度Q 学习（Deep Q－Learning，DQN）算法进行对比，以验证不同移动性下算法的稳定性及其表现。 算法的学习率设定为0.005，实验结果如图3 所示。 随着平均车辆移动速度的增加，各算法的平均服务延迟都在上升，这是由于车辆行驶速度越快，离开RSU 通信范围的间隔也就越小，服务迁移的触发频率随之上升。 本文和DQN 算法的平均服务延迟都处于较低的水准，同时其增长速率也较为缓慢。 AMC 算法虽然每次都选择就近的RSU，但是迁移服务时带来的额外开支并不能弥补其服务延迟。 与DQN 算法相比，本文提出的算法在移动速度为20 km／h 时有8.6%的优势，当移动速度达到60 km／h 时有15.3%的优势，这是由于本文提出的算法具有较高的探索率，相比DQN 算法可以探索更多的迁移决策，从而使得平均服务时延上升速度较为缓慢。

图3 不同车辆移动速度下的平均服务延迟Fig. 3 Average service delay for different vehicle movement speeds

3.2.3 不同算法的能耗对比

对比各算法在不同车辆移动速度下的平均能耗，实验结果如图4 所示，随着平均车辆移动速度的增加，各算法的能耗同步上升，其中AMC 算法的上升速率最快，这是由于车辆移动速度的上升导致车辆更快的离开RSU 通信范围，进而频繁触发迁移行动，AMC 算法的能耗因此远远高于其他算法。 而Random 算法在远离RSU 后并没有完全决定迁移，因此相比AMC 算法其能耗仍有一定优势。 基于强化学习的DQN 和本文算法具有较大的优势，这是因为奖励函数中能耗带来的奖励值使得算法对于迁移决策较为慎重，频繁地触发服务迁移并不总是最优策略。 与DQN 相比，本文提出的算法在60 km／h 移动状态下有14.4%的优势，这是由于该算法在训练过程中充分探索了可能的策略，因而与DQN 相比能使用更优的策略以降低能耗水平。

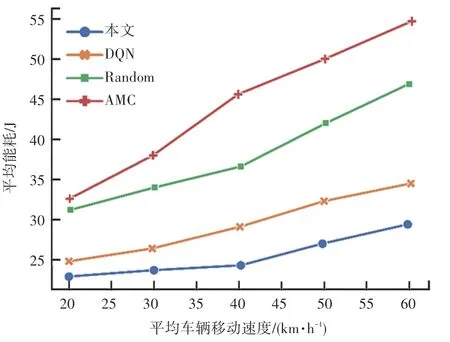
图4 不同车辆移动速度下的平均能耗Fig. 4 Average energy consumption for different vehicle movement speeds

4 结束语

针对中国目前重点发展方向之一的车联网，本文研究了基于该环境下的服务迁移问题，并对服务迁移过程中产生的计算成本、迁移成本和能耗建模，将迁移决策规划为部分迁移而非二元迁移，同时考虑了车辆移动性带来的问题。 本文将服务迁移建模为MDP 问题，并提出了基于深度强化学习的服务迁移算法来降低服务的平均时延和能耗。 实验结果表明，本文提出的算法在学习率为0.005 时能够较快达到收敛，并且与其他算法相比在20 km／h 和60 km／h 时分别有8.6%和15.3%的性能提升，同时当移动速度处于60 km／h 时，在能耗方面有14.4%的优势。 在未来工作中，将车辆加速度引入以预测用户驾驶车辆的移动意图，从而进行更精确的迁移决策。