弧面分度凸轮机构六自由度刚柔耦合动力学模型的研究*

李成平

（陕西国防工业职业技术学院，陕西 西安 710300）

凸轮结构在自动机床、轻工机械和机电一体化产品中得到广泛应用。当凸轮受输入力的作用连续转动时，会带动分度盘周期性间歇运动，所引起的惯性载荷使从动件的运动规律发生变化，导致凸轮机构输出的动态响应与理论值存在偏差。为了提高凸轮机构的定位精度和动态特性，需要在提高其零部件几何精度的同时，充分研究凸轮机构的动力学问题，掌握最佳的激励状态。笔者针对弧面分度凸轮机构，结合机械振动力学和弹性力学知识，建立了一种等效的模型来有效模拟其实际情况，建立了六自由度刚柔耦合动力学分析的数学方程[1-2]，为弧面分度凸轮的动力学研究提供借鉴。

1 动力学模型的建立

1.1 刚柔耦合动力学模型

刚体动力学假设所有构件都是刚体，从而进行动力学分析，过程相对简单，但难以模拟机构受力后的动态响应。柔性动力学考虑构件本身的弹性，从而对其进行动力学分析，能更加真实地还原机构的动态响应情况，但在分析过程中需要将弹性体拆分为多个自由度的离散系统，增加了系统的求解参数，动力学分析方程的求解难度也大大增加[3]。

充分考虑刚体动力学求解难度小、柔性动力学接近真实情况等特点，将精度要求较高或者高速工况下较容易发生变形的构件假设为弹性体，将不容易发生变形或者变形对输出结果影响较小的构件假设为刚体，构建由弹性体和刚性体组成的机械系统，从而进行动力学分析。这样不仅最大限度地模拟了机构实际动态性能，而且降低了动力学模型方程的建立与求解难度。

1.2 柔性动力学模型的建立

弧面分度凸轮机构由输入轴、凸轮、分度盘、滚子、输出轴、工位盘等组成。根据结构特点，采取质量集中的方法，把弧面凸轮分度机构离散为有3 个质量点和6 个自由度的系统，3 个质量点分别集中于弧面分度凸轮机构的分度盘、凸轮和载荷盘上。该系统的每个质量点均具有质量m、刚度k和阻尼C。考虑凸轮扭转振型、分度盘与载荷盘的扭转与平动振型，建立该机构动力学模型[4-7]，如图1 所示。

图1 弧面分度凸轮机构柔性动力学模型

弧面分度凸轮机构的输出轴为细长轴，容易发生变形；其凸轮和分度盘的长径比相对较小、刚度相对较大，变形通常可以忽略。

1.3 刚柔耦合动力学模型的建立

根据刚柔耦合动力学模型的相关研究方法，弧面分度凸轮机构的输出轴为回转体，具有一定的长度，运动过程中会发生扭转变形和弯曲变形，直接影响分度盘的定位精度，在动力学分析时需要考虑；凸轮与滚子啮合部位的挠度相对较小，为简化动力学模型，降低分析难度，弯曲变形可以忽略；输入轴较短且长径比较小，刚度相对较大且不易发生变形，可以忽略不计。因此，在弧面分度凸轮机构的刚柔耦合动力学模型建立过程中，可以将输出轴与载荷盘认定为柔性体，将输入轴、凸轮、分度盘等构件认定为刚体，即在研究弧面分度凸轮机构动力学时，只需针对其输出系统开展研究。同时，载荷盘安装在输出轴上，根据质量集中法，可将两者集中为一个等效质量点，假设等效质量点构件质量为m，建立输出系统动力学模型，如图2所示。

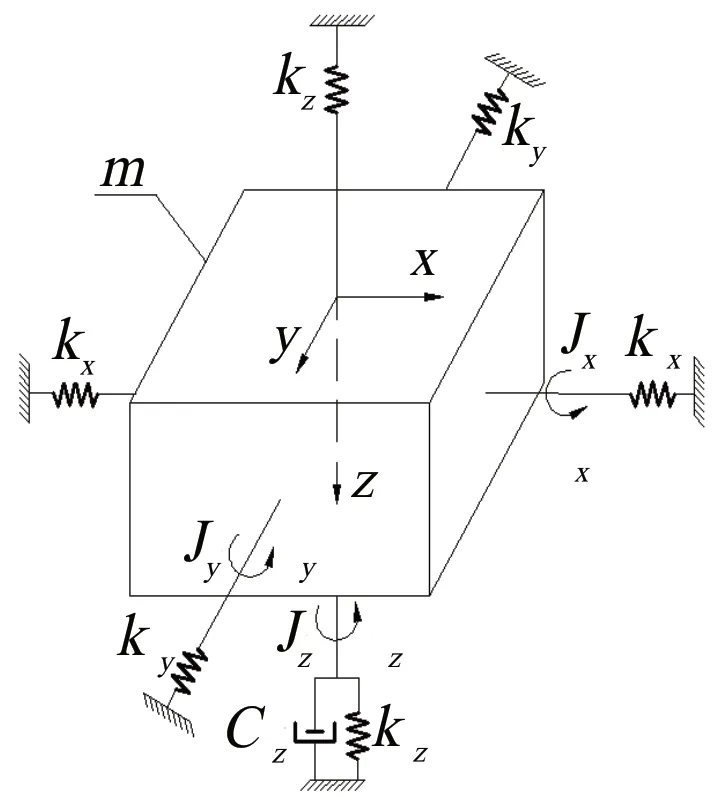
图2 弧面分度凸轮机构输出系统动力学模型

在弧面分度凸轮机构输出系统动力学模型中，等效质量体在坐标系中有六个自由度，分别是x、y、z三个坐标轴的轴向振动和绕轴转动。其中，质量体绕x、y、z三个轴的转动惯量分别为Jx、Jy、Jz，由于载荷盘与输出轴为绕z轴的回转体，故Jx≈Jy。

根据弧面分度凸轮机构输出系统等效质量体动力学模型，建立其动力学方程[8-10]。输出系统动力学模型中存在的扭转变形会产生非线性因素，因此对其进行线性处理：

其中，τ、.τ、..τ分别为机构输出系统等效质量体的理论转角、角速度与角加速度；qx、qy、qz分别为机构输出系统等效质量体绕x、y、z轴的等效转角；θx、θy、θz分别为机构输出系统等效质量体绕x、y、z轴的实际转角。

由于等效质量体的等效转角很小，可等效为线位移。因此，qx=θx-τ(θ)；qy=θy-τ(θ)；qz=θz-τ(θ)。

x、y、z，kx、ky、kz，kθx、kθy、kθz分别为机构输出系统等效质量体在x、y、z方向线位移、等效抗弯刚度、等效扭转刚度；Cθz为等效质量体绕z轴转动的阻尼系数。

由于载荷盘与输出轴为绕z轴的回转体，所以其在x、y方向的等效抗弯刚度与等效扭转刚度相似。故kx≈ky，kθx≈kθy。

1.4 动力学模型数学方程的建立

建立弧面分度凸轮机构的系统动力学方程：

将式（2）至（7）代入式（8）中，得到该机构动力学方程的参数矩阵。

1）广义坐标矩阵：

在图1 所示的弧面分度凸轮机构柔性动力学模型中，当凸轮顺时针转动时，凸轮和分度盘的啮合作用会带动分度盘逆时针转动。以坐标轴的正方向移动为线位移正向，沿坐标轴的逆时针方向为转角正向。

2）质量矩阵：

3）阻尼矩阵：

弧面分度凸轮机构在实际工作过程中存在多种阻尼，通常情况下，该类阻尼对输出的影响较小，可不做研究；但当激振频率接近机构的固有频率时，可能会出现共振的现象，其影响会显著增强，阻尼的影响也必须考虑，其振型为：

按振型阻尼处理可得：

4）惯性载荷矩阵：

在弧面分度凸轮机构输出系统中，载荷的形式主要有惯性力和摩擦力。该机构属于高精密零件，摩擦力很小，可以忽略，因此只考虑惯性载荷，其惯性载荷矩阵为：

5）刚度矩阵：

1.5 动力学模型的固有频率计算

根据以上动力学方程和参数，采用模态叠加法，将时间离散为单元时间，并将凸轮机构视为定常系统，以此求解式（8）的矩阵方程：

求解方程（16），可得各阶固有频率ωr和对应的各阶振型矢量ϕr(r=1,2,…,n)，n为振型数，在弧面分度凸轮机构输出系统中，n=6。

求解以上方程，得弧面分度凸轮机构的固有频率方程：

2 结论

笔者以机械振动理论和刚柔耦合理论为基础，综合考虑弧面分度凸轮机构各结构弹性变形对其动力学的影响，建立了弧面分度凸轮机构六自由度动力学模型和固有频率的求解方程，为此类机构进行动力学分析提供了参考。