大体积混凝土墙水化放热温度场分析
李志鹏,罗奇星,韩庆华,张晋元,孙加齐
大体积混凝土墙水化放热温度场分析
李志鹏1, 2, 3,罗奇星3,韩庆华1, 2, 3,张晋元1, 2, 3,孙加齐4
(1. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学),天津 300350;2. 滨海土木工程结构与安全教育部重点实验室(天津大学),天津 300350;3. 天津大学建筑工程学院,天津 300350;4. 中国建筑第八工程局有限公司,上海 200112)
为有效进行大体积混凝土施工温度控制,对大体积混凝土施工过程中温度场分布规律进行研究.针对混凝土水化放热过程中内热源随时间变化的问题,采用杜哈美尔定理推导出第三类边界条件下大体积混凝土墙水化放热温度场的解析解.由大体积混凝土墙水化放热温度场解析解可知,混凝土水化放热过程中,混凝土内某一点温度随时间增加先增大后减小,且温度变化近似符合指数函数之和;某一时刻混凝土内温度从核心到表面逐渐降低,且温度分布近似符合三角函数.结合解析解与数值分析方法研究发现,随着混凝土厚度、入模温度、混凝土绝热温升和单方胶凝材料对应系数的增大,混凝土养护阶段核心最高温度升高,导致混凝土里表温差增大;随着表面传热系数增加,混凝土养护阶段核心最高温度和表面温度降低,但是混凝土里表温差增大.混凝土内最大自约束应力正比于里表温差,因此通过分层浇筑、降低混凝土的入模温度、减小混凝土表面传热系数、降低混凝土绝热温升值和单方胶凝材料对应系数等方式可以减小混凝土内最大自约束应力,降低大体积混凝土开裂风险.
混凝土水化热;温度场;杜哈美尔定理;解析解;温度控制
大体积混凝土广泛应用于大型设备的基础、挡墙、大坝等工程中.混凝土水化放热使混凝土温度上升,混凝土表面与环境接触降温较快,混凝土内部热量积聚不易散失,由此产生的不均匀温度场会导致混凝土开裂,影响正常使用和结构寿命[1-5].
目前,工程领域常用的混凝土水化内部温度计算方法只限于计算混凝土不同龄期内部最高温度,无法得到混凝土内温度分布,同时未能考虑边界条件对混凝土温度场的影响[6-8].计算混凝土温度场可采用解析方法和近似方法.解析方法能够得到函数形式的解答,Chen等[9]采用分离变量法推导出无内热源情况下含非金属冷却水管的大体积混凝土温度场解析解,胡孟娣等[10]采用分离变量法推导出内嵌管式辐射供暖时混凝土楼板的温度场解析解,余志武等[11]采用傅里叶变换法推导出火灾下钢筋混凝土板内温度场解析解,也有相关学者采用杜哈美尔定理推导出边界温度改变后混凝土板一维温度场解析解[12],而关于大体积混凝土水化放热过程中温度场解析解的研究鲜见报道.近似方法[13]包括差分法、边界元法、有限元法等数值解法,能够得到混凝土内部各离散节点的温度近似值,当单元数目较多时接近实际情况,但是并不清楚混凝土内部温度场的分布及变化规律.因此,有必要进行大体积混凝土水化放热温度场分布及变化规律的研究.
本文采用杜哈美尔定理[14]推导大体积混凝土墙水化放热温度场解析解,结合解析解与数值分析结果,研究混凝土厚度g、入模温度0、表面传热系数、绝热温升、单方胶凝材料对应系数对大体积混凝土温度场的影响,从而给出大体积混凝土施工的温度控制建议.
1 大体积混凝土墙水化放热温度场的解析解
由《大体积混凝土施工标准》(GB 50496—2018)[15]可知,混凝土水化放热过程中温度是关于时间的函数.由于温度变化范围不大,可将材料的密度、表面传热系数、导热系数、比热容等参数视为常数.内热源随时间变化的常物性三维非稳态导热微分方程为

工程结构中常见的大体积混凝土墙在长、宽方向的尺寸比厚度方向大得多,混凝土浇筑体中大部分区域的温度沿厚度方向显著变化,可以将大体积混凝土水化放热简化为一维无限大平壁(以下简称平壁)导热问题[2].
混凝土表面与外界环境进行对流换热,符合第三类边界条件[16].热流密度与混凝土表面温度w和环境温度f之差成正比,即
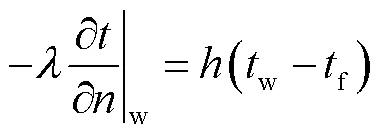
根据规范[15],混凝土绝热温升曲线可简化为

式中:绝热温升值通过试验得到;与水泥品种、用量和入模温度等有关.
因此,内热源函数

如图1所示,平壁厚2,坐标轴原点位于平壁中分面,初始温度0、环境温度f、内热源函数()随时间变化,表面传热系数为常数,平壁两半的温度分布完全对称,故中分面为绝热面,只需考虑半个平壁即可.平壁导热微分方程、边界条件、初始条件为

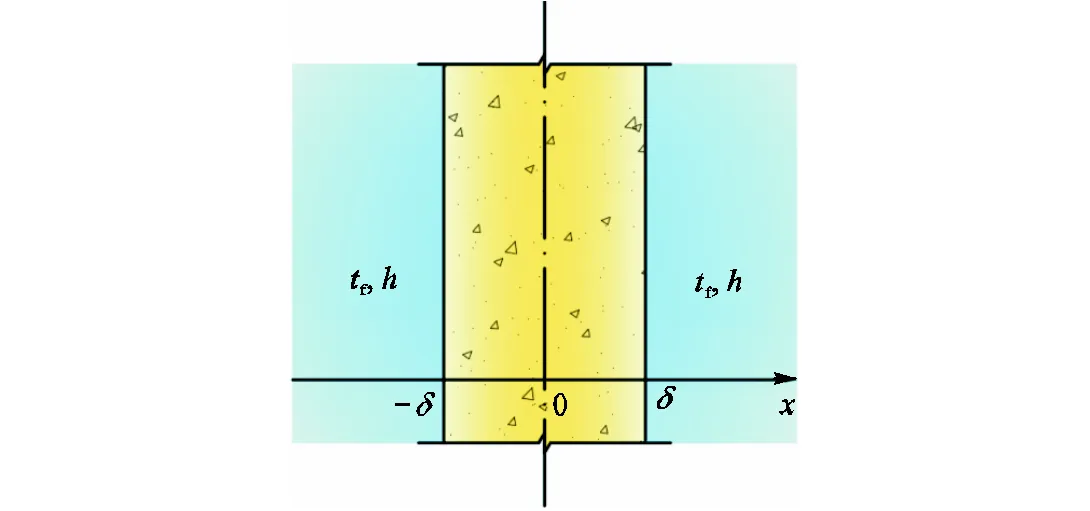
图1 一维无限大平壁

对于内热源随时间变化的导热问题,根据杜哈美尔定理,引入与时间无关的参量,即
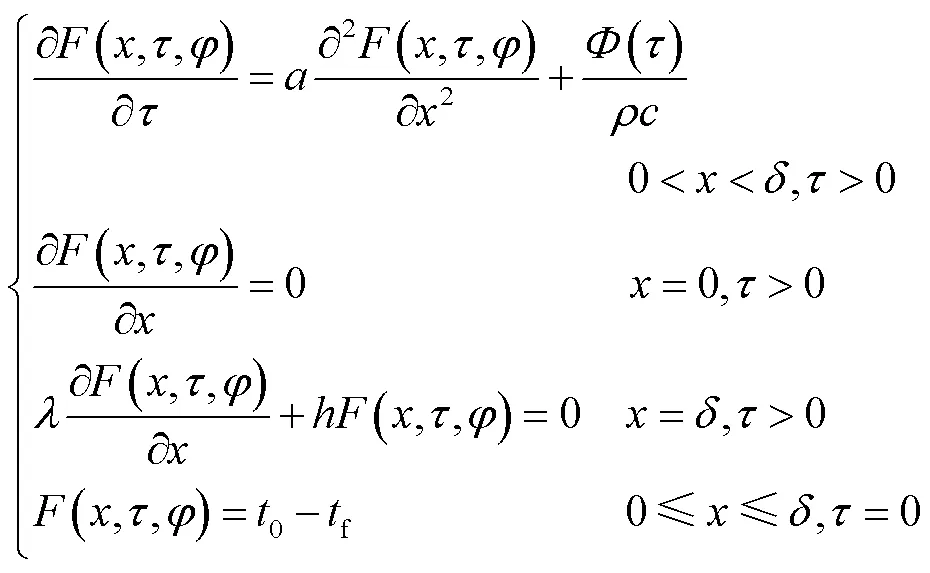
则式(6)的解可以用式(7)的解表示为
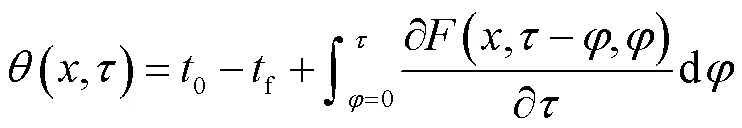

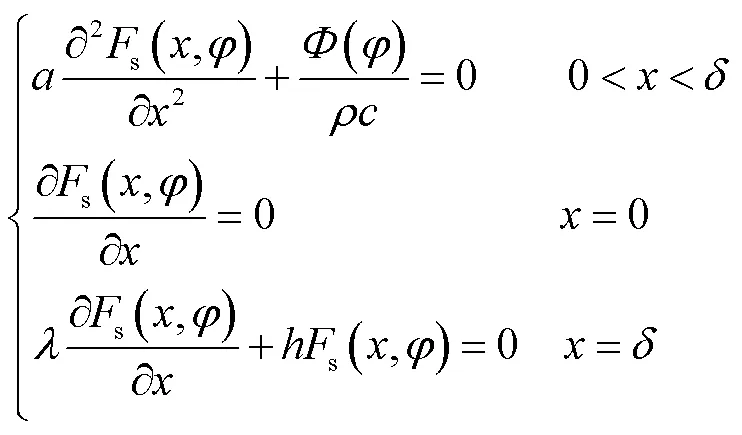

则式(7)的解可根据式(8)求得为

对于式(9),采用分离变量法解得
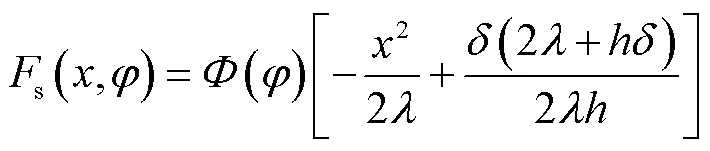
式(10)为有限大物体一维齐次问题,由文献[14]可知,其解为



将式(12)和(13)代入式(11),可得式(7)的解为


根据杜哈美尔定理,将式(4)、式(13)和式(14)代入式(8),可得式(6)的解为

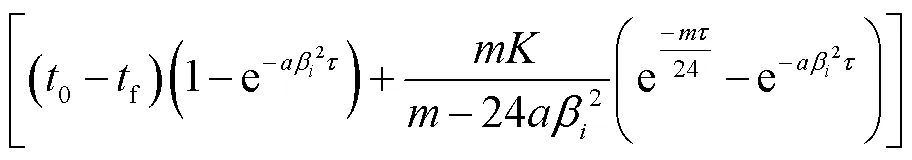
因此,大体积混凝土墙水化放热温度场的解析 解为

其中

2 大体积混凝土墙水化放热的数值模拟
以大体积混凝土墙为例,采用Midas软件进行数值建模分析[17],建模参数如表1所示.底部为一整块混凝土,顶部与空气直接接触,两侧为18mm厚木模板,Midas模型如图2所示,模型三视图如图3所示.两侧模板面积较大,在混凝土对流换热过程中起主导作用;顶面对流换热和底面热传导对墙体温度影响较小;墙体较长,忽略端部对流换热,基本符合一维无限大平壁假设.本算例中,大体积混凝土墙温度在浇筑后36h达到峰值,此时结构内有最大里表温差.
表1 建模参数

Tab.1 Modeling parameters

图2 大体积混凝土墙模型
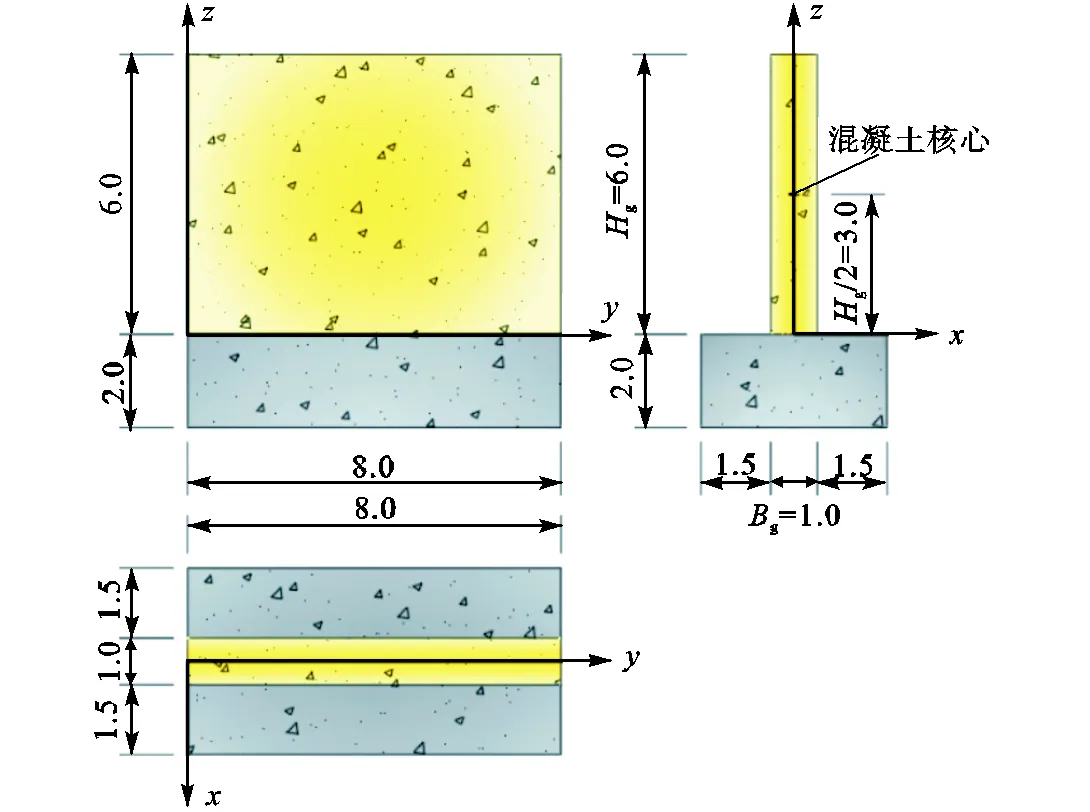
图3 大体积混凝土墙三视图(单位:m)
式(16)是无穷级数求和式,令


由式(18)可知,混凝土水化放热过程中,混凝土内某一点温度随时间增加先增大后减小,且温度变化近似符合指数函数之和;某一时刻混凝土内温度从核心到表面逐渐降低,且温度分布近似符合三角函数.
图4为大体积混凝土核心温度随时间变化曲线.混凝土浇筑后,混凝土水化放热,混凝土温度升高;混凝土温度高于环境温度后,混凝土与环境进行对流换热,混凝土温度降低;混凝土水化放热速率随时间增加逐渐降低,对流换热速率随混凝土与环境温差增加而提高,因此,混凝土的核心温度呈现先升高后降低的变化规律.图5为大体积混凝土墙温度达到峰值时大体积混凝土内部3m标高处温度变化曲线.由混凝土截面中心到表面,温度逐渐降低.

图4 大体积混凝土核心温度曲线
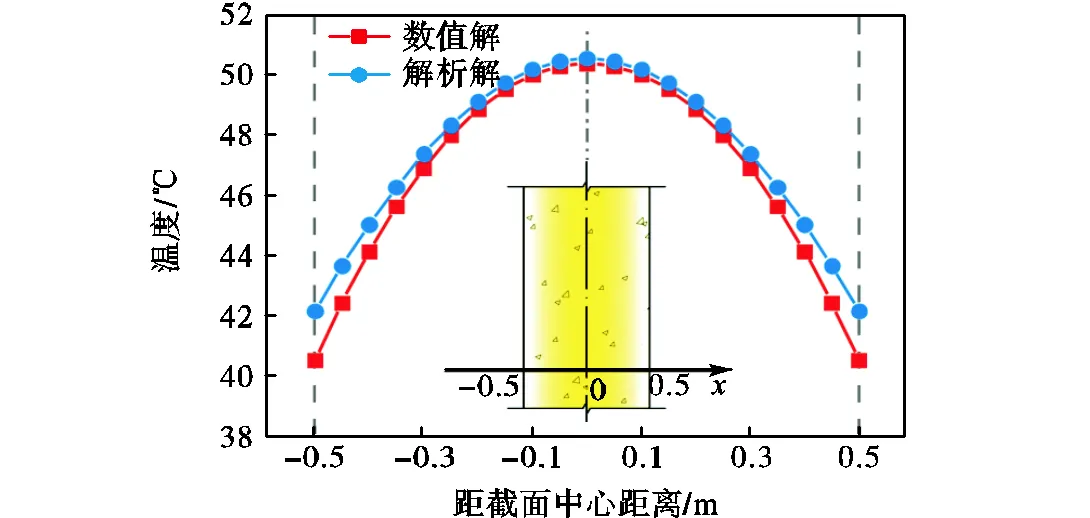
图5 36h时大体积混凝土温度分布(z=3.0m)
Fig.5 Temperature distribution of the mass concrete at 36h(z=3.0m)
3 大体积混凝土养护的温度控制
混凝土内温度沿截面非线性变化时将产生温度应力[1].由式(18)可得温度梯度为

由式(19)可知,混凝土内温度沿截面非线性变化,当混凝土核心达到最高温度时,混凝土表面有最大温度梯度.混凝土内部温度较高,表面温度较低,因此混凝土表面受拉,拉应力超过混凝土抗拉极限承载力后混凝土表面开裂.
根据规范[15],混凝土最大自约束应力

由式(20)可知,混凝土内最大自约束应力正比于里表温差.为了研究混凝土厚度g、入模温度0、表面传热系数、混凝土属性对大体积混凝土水化放热温度的影响,采用解析方法和数值解法对大体积混凝土墙进行分析,分析参数如表2所示.
3.1 混凝土厚度Bg对大体积混凝土养护温度的影响
大体积混凝土厚度g对大体积混凝土养护温度的影响如图6所示.混凝土导热性能较差,随着厚度g的增大,混凝土养护阶段的核心最高温度升高,增速放缓.因此,对于大体积混凝土结构,采用分层浇筑的方式能有效降低大体积混凝土水化放热过程中的温度.
表2 大体积混凝土养护温度控制分析参数

Tab.2 Analytical parameters of the mass concrete curing temperature control
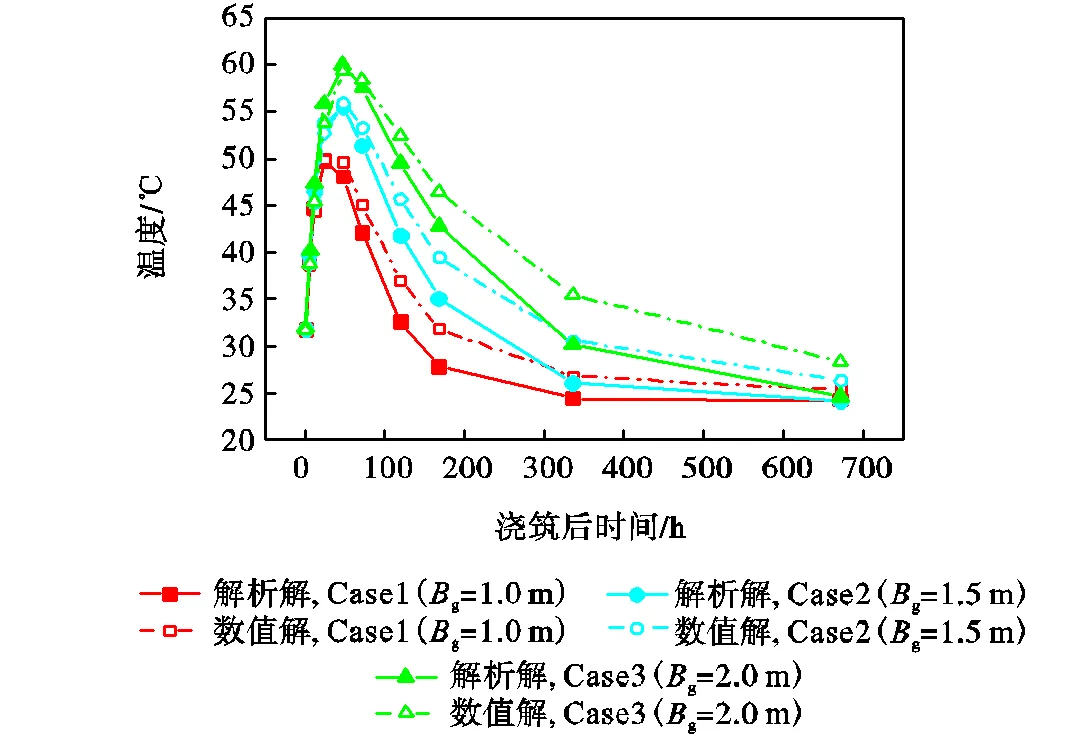
图6 厚度Bg变化时大体积混凝土核心温度曲线
浇筑24h后,混凝土迅速变化,且核心温度较高,此时Case1~Case3的解析解相较于数值解的偏差分别为0.07%、1.82%和3.76%,偏差较小.浇筑28d后,Case1~Case3的解析解相较于数值解的偏差分别为4.07%、8.35%和13.08%.可见随着混凝土墙体高厚比的增加,解析解相较于数值解的偏差增大.考虑到计算精度,当混凝土墙体高厚比小于3时,不宜简化为一维平面问题.
3.2 入模温度t0对大体积混凝土养护温度的影响
大体积混凝土入模温度0对养护温度的影响如图7所示.随着入模温度0的升高,混凝土温度整体升高,最终接近环境温度.
因此,对于大体积混凝土结构,适当降低混凝土的入模温度0能有效降低大体积混凝土水化放热过程中的温度.

图7 入模温度t0变化时大体积混凝土核心温度曲线
3.3 表面传热系数h对大体积混凝土养护温度的影响
大体积混凝土表面传热系数对养护温度的影响如图8所示,大体积混凝土最大里表温差的变化如表3所示.随着表面传热系数的增加,混凝土与环境热交换加快,混凝土养护阶段核心最高温度和表面温度降低,但是混凝土里表温差增大,最大自约束应力增大.

图8 表面传热系数h变化时大体积混凝土核心温度曲线
表3 表面传热系数变化时大体积混凝土里表温差

Tab.3 Temperature difference between core and surface of mass concrete with varying surface heat transfer coefficientsh
因此,通过覆盖保温材料等方式,增加混凝土表面热阻,减小混凝土表面传热系数,可以降低大体积混凝土开裂风险.
3.4 混凝土属性对大体积混凝土养护温度的影响
大体积混凝绝热温升和单方胶凝材料对应系数对养护温度的影响如图9和图10所示,大体积混凝土最大里表温差的变化如表4和表5所示.随着混凝土绝热温升的增大,混凝土水化放热增加,混凝土温度和里表温差增大.随着单方胶凝材料对应系数增大,混凝土绝热温升曲线变陡峭,混凝土放热速度变快,升温阶段混凝土温度升高,里表温差增大.
因此,通过降低混凝土绝热温升和单方胶凝材料对应系数,可以降低大体积混凝土水化放热过程中的温度和里表温差.选用合适的水泥类型,减少水泥用量,添加粉煤灰、矿渣等外加剂,降低入模温度等方式均可降低混凝土绝热温升和单方胶凝材料对应系数.

图9 绝热温升K变化时大体积混凝土核心温度曲线

图10 m值变化时大体积混凝土核心温度曲线
表4 绝热温升变化时大体积混凝土里表温差

Tab.4 Temperature difference between core and surface of mass concrete with varying adiabatic tem-perature rise values K
表5值变化时大体积混凝土里表温差

Tab.5 Temperature difference between core and surface of mass concrete with varying m values
4 结 论
本文推导了大体积混凝土墙水化放热温度场解析解,研究了混凝土厚度g、入模温度0、表面传热系数、绝热温升、单方胶凝材料对应系数对大体积混凝土温度场的影响,给出了大体积混凝土施工的温度控制建议.
(1) 从大体积混凝土墙水化放热温度分布函数可以看出:混凝土水化放热过程中,混凝土内某一点温度变化近似符合指数函数之和;某一时刻混凝土内温度分布近似符合三角函数.
(2) 当混凝土墙体高厚比大于3时,可简化为一维平面.某一时刻混凝土内温度梯度变化近似符合三角函数.当混凝土核心温度最高时,混凝土表面有最大温度梯度.
(3) 随着厚度g、入模温度0、混凝土绝热温升和单方胶凝材料对应系数的增大,混凝土养护阶段核心最高温度升高,将导致混凝土里表温差增大;随着表面传热系数的增加,混凝土养护阶段核心最高温度和表面温度降低,但是混凝土里表温差 增大.
(4) 分层浇筑、降低混凝土的入模温度、减小混凝土表面传热系数、降低混凝土绝热温升值和单方胶凝材料对应系数,可以降低大体积混凝土开裂风险.
[1] 王铁梦. 工程结构裂缝控制[M]. 2版. 北京:中国建筑工业出版社,2017.
Wang Tiemeng. Crack Control of Engineering Structures [M]. 2nd ed. Beijing:China Architecture and Building Press,2017(in Chinese).
[2] 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京:中国电力出版社,1998.
Zhu Bofang. Temperature Stress and Temperature Control of Mass Concrete[M]. Beijing:China Electric Power Press,1998(in Chinese).
[3] 杨大平. 大体积高性能混凝土温度应力控制试验研究[D]. 西安:西安建筑科技大学,2006.
Yang Daping. Exerimental Study on Mass HPC Temperature and Stress Control[D]. Xi’an:Xi’an University of Architecture and Technology,2006(in Chinese).
[4] 魏德敏,洪川海,李重阳,等. 大体积混凝土基础的水管冷却温度场研究[J]. 天津大学学报(自然科学与工程技术版),2016,49(6):437-442.
Wei Demin,Hong Chuanhai,Li Chongyang,et al. Temperature field of mass concrete foundation with pipe-cooling[J]. Journal of Tianjin University(Science and Technology),2016,49(6):437-442(in Chinese).
[5] 卢哲安,陈 猛,任志刚. 桥墩承台大体积混凝土的温度控制[J]. 混凝土,2008(4):97-99.
Lu Zhe’an,Chen Meng,Ren Zhigang. The control of temperature in massive concrete of Hou-hu bridge’s No.14 cap[J]. Concrete,2008(4):97-99(in Chinese).
[6] 贺 云,贺金龙,余 棚,等. 索塔承台大体积混凝土温度控制研究[J]. 铁道科学与工程学报,2020,17(2):372-378.
He Yun,He Jinlong,Yu Peng,et al. Study on temperature control of mass concrete for tower pile cap[J]. Journal of Railway Science and Engineering,2020,17(2):372-378(in Chinese).
[7] Husein M A I,Mutasher S A,Qiu T J. Thermal-structure modeling and temperature control of roller compacted concrete gravity dam[J]. Jounal of Perform-ance of Constructed Facilities,2003,17(4):177-187.
[8] Majora C E,Zavarise G,Borsetto M,et al. Nonlinear analysis of thermal stresses in massive concrete castings[J]. Cement and Concrete Research,1990(7):559-578.
[9] Chen Guorong,Ding Xiaofei,Cai Mingxuan,et al. Analytical solution for temperature field of nonmetal cooling pipe embedded in mass concrete[J]. Applied Thermal Engineering,2019,158:113774.
[10] 胡孟娣,彭钦磊. 内嵌管式辐射地板传热简化模型研究[J]. 建筑科学,2012,28(6):106-109.
Hu Mengdi,Peng Qinlei. Development of simplified thermal model of pipe-embedded radiant floors[J]. Building Science,2012,28(6):106-109(in Chinese).
[11] 余志武,王中强,蒋丽忠. 火灾下钢筋混凝土板的温度场分析[J]. 铁道科学与工程学报,2004,1(1):58-61.
Yu Zhiwu,Wang Zhongqiang,Jiang Lizhong. Analysis of temperature field in reinforced concrete slabs exposed to fire[J]. Journal of Railway Science and Engineering,2004,1(1):58-61(in Chinese).
[12] 唐松花,罗迎社,彭相华. 火灾情况下混凝土板温度场的解析解[J]. 应用力学学报,2013,30(4):544-549.
Tang Songhua,Luo Yingshe,Peng Xianghua. Analytical solutions of temperature field in the concrete slab on fire[J]. Chinese Journal of Applied Mechanics,2013,30(4):544-549(in Chinese).
[13] 张晓飞. 大体积混凝土结构温度场和应力场仿真计算研究[D]. 西安:西安理工大学,2009.
Zhang Xiaofei. Simulation and Study on Temperature and Stress Fields for Mass Concrete Structure[D]. Xi’an:Xi’an University of Technology,2009(in Chinese).
[14] 奥齐西克 M N. 热传导[M]. 北京:高等教育出版社,1983.
Ozisik M N. Heat Conduction[M]. Beijing:Higher Education Press,1983(in Chinese).
[15] 中华人民共和国住房和城乡建设部. GB 50496—2018 大体积混凝土施工标准[S]. 北京:中国建筑工业出版社,2018.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50496—2018 Standard for Construction of Mass Concrete[S]. Beijing:China Architecture and Building Press,2018(in Chinese).
[16] 赵镇南. 传热学[M]. 3版. 北京:高等教育出版社,2019.
Zhao Zhennan. Heat Transfer[M]. 3rd ed. Beijing:Higher Education Press,2019(in Chinese).
[17] 汪建群,魏桂亮,刘 杰,等. 跨海大桥大体积混凝土承台水化热实测与分析[J]. 桥梁建设,2020,50(3):25-31.
Wang Jianqun,Wei Guiliang,Liu Jie,et al. Measurement and analysis of hydration heat in massive concrete pile cap of a sea-crossing bridge[J]. Bridge Construc-tion,2020,50(3):25-31(in Chinese).
[18] 中华人民共和国住房和城乡建设部. GB 50010—2010 混凝土结构设计规范[S]. 北京:中国建筑工业出版社,2015.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50010—2010 Code for Design of Concrete Structures[S]. Beijing:China Architecture and Building Press,2015(in Chinese).
[19] 龚召熊. 水工混凝土的温控与防裂[M]. 北京:中国水利水电出版社,1999.
Gong Zhaoxiong. Temperature Control and Crack Prevention of Hydraulic Concrete[M] Beijing:China Water and Power Press,1999(in Chinese).
[20] 翟希梅,王 恒. 160000 m3大型LNG储罐混凝土外罐施工全过程温度作用分析[J]. 哈尔滨工业大学学报,2016,48(6):92-97.
Zhai Ximei,Wang Heng. Influence factors of thermal stress in the construction period of the concrete outer tank for 160000 m3LNG storage[J] Journal of Harbin Institute of Technology,2016,48(6):92-97(in Chinese).
Analytical Solution for the Temperature Field of the Hydration Heat in a Mass Concrete Wall
Li Zhipeng1, 2, 3,Luo Qixing3,Han Qinghua1, 2, 3,Zhang Jinyuan1, 2, 3,Sun Jiaqi4
(1. Key Laboratory of Earthquake Engineering Simulation and Seismic Resilience of China Earthquake Administration(Tianjin University),Tianjin 300350,China;2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education(Tianjin University),Tianjin 300350,China;3. School of Civil Engineering,Tianjin University,Tianjin 300350,China;4. China Construction Eighth Engineering Division Co.,Ltd.,Shanghai 200112,China)
To effectively control the temperature of mass concrete construction,the temperature field distribution law of this process is studied in this paper. The internal heat source changes with time during the hydration heat release. To address this issue,the analytical solution for the hydration heat release temperature field in a mass concrete wall un-der the third boundary condition is derived by the Duhamel’ theorem. Based on this analytical solution,it is found that when the hydration heat is released,the temperature of the concrete first increases and then decreases with time,and the temperature change is approximately in accordance with the sum of exponential functions. In addition,the temperature of the concrete decreases gradually from the core to the surface at a given time,and the temperature distribution approximately follows a trigonometric function. Through the analytical solution and numeri-cal analysis,it is found that with the increases in concrete thickness,the temperature of the mixture placed into the mold,adiabatic temperature rise value,and the coefficient of the cementitious material per cubic meter(value),the maximum core temperature of the concrete in the curing stage increases,thereby increasing the temperature difference between the core and the surface of the concrete. Moreover,with the increased surface heat transfer coefficient,the maximum temperatures of the core and surface of the concrete in the curing stage decrease while the temperature difference between the concrete core and surface increases. The maximum self-equilibrating stress in the concrete is proportional to the temperature difference between its core and surface. Therefore,the maximum self-equilibrating stress and the risk of concrete cracking can be reduced by pouring it in layers and reducing the temperature of the mixture placed into the mold,surface heat transfer coefficient,adiabatic temperature rise value,andvalue of the concrete.
concrete hydration heat;temperature field;Duhamel’s theorem;analytical solution;temperature control
10.11784/tdxbz202204036
TU398.5
A
0493-2137(2023)08-0878-08
2022-04-16;
2022-07-29.
李志鹏(1982— ),男,硕士,高级工程师,zhipeng.li@tju.edu.cn.Email:m_bigm@tju.edu.cn
韩庆华,qhhan@tju.edu.cn.
天津市自然科学基金资助项目(21JCZDJC00410,22JCYBJC00620).
the Natural Science Foundation of Tianjin,China(No. 21JCZDJC00410,No. 22JCYBJC00620).
(责任编辑:金顺爱)

